基于超螺旋算法的永磁同步电动机直接转矩自抗扰控制

杨明晖， 李生权， 李 喆， 冯 波， 李 娟

(扬州大学 电气与能源动力工程学院， 江苏 扬州 225127)

当前主流的电动机调速控制技术主要有矢量控制(field-oriented control，FOC)和直接转矩控制(direct torque control，DTC).与FOC相比，DTC具有优良的快速性、准确性以及鲁棒性且无需复杂的坐标变换计算，因此提高了控制系统的运算速度[1-3].传统DTC因采用2个Bang-Bang控制器分别对转矩和磁链进行控制，导致磁链和转矩脉动大的问题，使得逆变器开关频率不稳定，从而影响系统低速时调速性能.

对于DTC存在的问题，各国学者们进行了研究并提出了许多优化方案.文献[4-5]中提出在传统DTC的开关表中增加零电压矢量，该方案可有效缓解由磁链和转矩引起的系统抖振问题，但磁链和转矩环仍采用Bang-Bang控制器，因此无法消除系统存在的脉动问题.文献[6]中提出用空间矢量脉宽调制(space vector pulse width modulation，SVPWM)技术代替传统DTC系统中的开关表，从而保持开关频率稳定，且分别以转矩和磁链误差作为输入，使用PI控制器替代Bang-Bang控制器来对磁链和转矩进行控制以提高系统稳定性，但PI控制器难以保证系统鲁棒性，从而影响精度.文献[7]中采用传统滑模控制(sliding mode control，SMC)，用SMC控制器替换传统DTC系统的Bang-Bang控制器，有效地减小系统中磁链和转矩脉动，但由于SMC存在着不连续的开关特性，使得控制系统存在脉动的问题无法解决.文献[8-9]中采用超螺旋算法，利用超螺旋滑模控制替换传统DTC系统中磁链、转矩环上的Bang-Bang控制，该算法不仅保留了传统滑模变结构控制的抗干扰能力强以及鲁棒性好等优点，还有效抑制滑模抖振缺陷，提高滑模的动态性能；该方案中速度控制器采用的是PI算法，该控制算法简单、易实现，但快速性和超调的矛盾难以协调.

针对这些问题，文中拟采用自抗扰控制器对永磁同步电动机的速度环进行调节，以提高系统的快速性和抗干扰能力[10].将传统DTC系统中的磁链环和转矩环上的Bang-Bang控制器都替换成超螺旋滑模(super-twisting sliding mode，STSM)控制器，以解决传统系统中存在的转矩、磁链脉动，进而改善系统的调速性能.

1 永磁同步电动机数学模型

如图1所示，定子磁链ψs在αOβ坐标系中的空间相位角为θ，定子磁链ψs与转子磁链ψf之间的夹角为δ又称负载角.

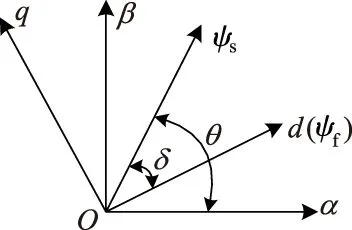
图1 αOβ与dOq坐标系间关系

进一步可得dOq坐标系下电磁转矩方程为

|ψs|(Lq-Ld)sin 2δ],

(1)

式中：Ld、Lq为d、q轴上的定子电感；p为极对数.文中研究对象为表贴式的永磁同步电动机(permanent magnet synchronous motor，PMSM)，则可理想化为定子电感满足Ld=Lq=Ls，电磁转矩方程可简化为

(2)

由式(2)可知，在定子磁链大小一定时，可以通过调节δ来改变电磁转矩Te大小.同时可得dOq坐标系下定子电压方程为

(3)

式中：ud、uq、id、iq、ψd、ψq分别为d、q轴上的定子电压、定子电流、定子磁链；Rs为定子电阻；wm为电动机的机械角速度.进而得到dOq坐标系下定子磁链方程为

(4)

进一步得到PMSM系统的运动方程为

(5)

式中：J为转动惯量；TL为负载转矩；B为阻尼系数.

2 基于DTC的PMSM调速设计

2.1 基于STSM的转矩和磁链控制器设计

与传统滑模控制将开关作用的控制量u应用到一阶导数的策略不同，超螺旋算法的主要思想是将u应用到高阶导数中，这可以在一定程度上抑制抖振现象，从而提高系统的控制精度.

为分析问题的方便，定义如下动态系统[11]：

(6)

式中：x为状态变量；u为输入控制量；y为系统的输出变量；a、b、c是与状态变量x相关的未知函数.从而STSM控制算法的控制律为

(7)

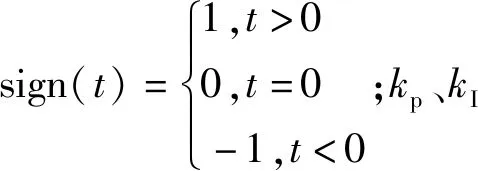
(8)

式中：AM表示A的绝对值的最大值；BM、Bm分别表示B的最大、最小值.其中A和B是与状态变量x相关的函数，满足

(9)

根据dOq坐标系下PMSM的数学模型和定子磁链矢量参考系，通过对磁链幅值进行连续求导，可推导出如下定子磁链微分方程：

(10)

进一步根据式(7)设计磁链控制器，如下：

(11)

同样对电磁转矩进行连续求导，可推导出如下电磁转矩微分方程：

(12)

进一步根据式(7)设计电磁转矩控制器，如下：

(13)

根据式(11)、(13)可得到超螺旋滑模控制器设计框图.

在仿真验证中引入超螺旋控制器后，减小了磁链和转矩脉动的问题，但电动机在低速运行段存在着控制效果差的问题，因此下一步将自抗扰控制器用于永磁同步电动机的速度环调节，以提高系统低速时的调速性能.

2.2 自抗扰速度控制器的设计

自抗扰控制方法是中科院韩京清[12]首创的一种主动抗干扰策略，在处理动态不确定性扰动、非线性等方面显示出独特的潜力.该方法将系统的外部干扰及内部未知因素视为总扰动，定义为一种新的状态——扩张状态，并通过估计和抵消进行动态补偿[13].

将式(5)改写成速度的微分形式：

(14)

(15)

基于式(15)设计的二阶线性ESO为

(16)

设计控制律，如下：

(17)

则自抗扰速度控制器结构图如图2中所示.

图2 基于超螺旋算法的永磁同步电动机直接转矩自抗扰速度控制系统框图

3 仿真结果及分析

文中将改进DTC与传统DTC进行仿真比较，结果如图3-5所示.由图3可见，传统DTC带载启动时超调量较大，调节时间较长，在给定转速为600 r·min-1的情况下，从开始启动到达到稳态用时超过0.05 s；而改进DTC从启动到达到稳态的过程平稳而迅速，没有超调.在0.2 s时刻，添加负载2 N·m，传统DTC转速有明显的突变，转速下降3%，且再次达到稳定状态需0.07 s；而改进DTC突变较小，转速下降0.5%，且到达稳态时间仅需0.02 s，快速性以及抗扰性提高近70%.

图3 转速对比曲线

图4 电磁转矩对比曲线

由图4可见，传统DTC的转矩脉动约为1.2 N·m，而改进DTC的转矩脉动约为0.4 N·m，转矩脉动降低近66%.

图5 磁链相图的变化曲线

由图5可清晰地看出改进DTC的磁链脉动更小，磁链轨迹更加平滑，这是由于磁链和转矩采用STSM控制，使得系统磁链脉动明显变小，磁链轨迹更加平滑.

4 结 论

文中针对传统DTC系统中存在的磁链、转矩脉动大的问题，将STSM控制算法运用于磁链环和转矩环的控制器中，并在此基础上引入自抗扰速度控制器.仿真结果表明：在相同条件下，文中所设计的改进DTC系统对超调有良好的抑制能力，面对负载转矩波动有更快的响应速度与更强的抗扰能力，所产生的磁链脉动更小，轨迹更加平滑.