时滞和扩散驱动下信息物理融合系统恶意病毒传播动力学
2022-11-07庄乾辉邱建龙梁金玲蒋海军
庄乾辉 ,肖 敏 ,王 赫 ,邱建龙 ,梁金玲 ,蒋海军
(1.南京邮电大学自动化学院人工智能学院,江苏南京 210023;2.临沂大学自动化与电气工程学院,山东临沂 276000;3.东南大学数学学院,江苏南京 210096;4.新疆大学数学与系统科学学院,新疆乌鲁木齐 830047)
1 引言
信息物理融合系统(cyber-physical systems,CPS)是多维异构的计算单元和物理对象在网络环境中高度集成交互的新型智能复杂系统,具有实时、鲁棒、自治、高效和高性能等特点[1].由于信息技术的高速发展,CPS已广泛应用于医疗设备、国防系统、自动化系统、智能电网以及智能空间等众多领域,是下一代产业革命的核心技术[2-5].
CPS内部节点作为连接网络系统和物理系统的桥梁,对恶意病毒的攻击非常敏感,以至于时常会产生无法满足人们预期要求的情形,从而引发系统故障或造成系统失调,最终导致众多CPS应用领域遭受严重损失[6-9],给国家基础设施和人民群众的生命财产安全带来巨大的威胁.2010年首次检测出的震网病毒能够定向攻击物理世界中基础能源设施,摧毁了伊朗核工厂和诸多工业企业[10].2012年出现的火焰病毒对一些国家的核设施和关键基础设施造成了巨大破坏.2017 年全球爆发的永恒之蓝勒索病毒,对多个国家政府、教育、医院、能源、通信、交通、制造等诸多关键信息基础设施进行了前所未有的毁坏.为了更好地分析恶意病毒在CPS中的传播机理,学者们将非线性动力学、信息物理融合系统和病毒传播理论[11]相结合,建立了SIR模型、SIRS模型、SIQR模型和SIQRS模型[12]等非线性CPS恶意病毒传播模型.上述模型成功揭示了恶意病毒在CPS内部的演化趋势和复杂动态特征.
恶意病毒的传播会致使CPS出现叉型、鞍结点、Neimark-Sacker、Hopf等多种分岔现象.其中,Hopf分岔是一种常见的动态分岔现象.目前,在Hopf分岔研究方面,已获得了许多重要成果[13-15].通过分析恶意病毒传播模型的Hopf分岔能够对恶意病毒的预测和控制提供战略指导.Yu[16]针对恶意病毒在CPS中的传播机理,建立了一个传播动力学模型以分析其Hopf分岔现象,并提出混合分岔控制策略控制Hopf分岔点的位置.Feng[17]提出了一种新的具有双重延迟和多状态反病毒措施的计算机病毒传播模型,利用稳定性和Hopf分岔理论,证明了恶意病毒传播的稳定性存在一个临界延迟值.Wang[18]建立了一类更具有一般性的多时滞恶意病毒传播模型,给出了系统稳定性和产生Hopf分岔的条件,并进一步研究了分岔点和感染率及预防效果系数的关系.
众所周知,恶意病毒传播是一种在空间和时间上都发生的现象.当CPS被某一类恶意病毒攻击时,CPS并不会立刻沦陷,恶意病毒在CPS中的每个节点状态传播时均需要一定的时间.然而,时间延迟的影响在文献[13]中被忽略了.另一方面,CPS中网络系统和物理系统连接的内部节点在空间分布中是不均匀的,在恶意病毒传播模型中引入描述空间位置的反应扩散,可以反映空间位置对恶意病毒传播的影响.然而,目前的许多工作大多局限于常微分方程,不能反应空间位置对恶意病毒传播的影响,如文献[11-12]和文献[14-16].为了更加精准刻画恶意病毒在信息物理融合系统中的演化,本文将已有的常微分方程模型扩展到偏微分方程模型,建立了一个具有时滞和扩散效应的恶意病毒传播模型,将病毒传播动力学从时间维度提升到时空维度.本文考虑了恶意病毒逐个攻破CPS内部节点并向下一节点传播的时间和感染节点从感染到隔离的时间,这两个因素会影响CPS的稳定性.此外本文还确定了扩散系数对图灵不稳定性的发生和时滞对Hopf分岔存在性的影响.
本文的其余部分组织如下: 在第2节中,提出了一个时空恶意软件传播模型,并通过计算给出了特征方程;在第3节中,只考虑扩散,研究了无时滞系统的图灵不稳定性;在第4节中,考虑时滞和扩散,证明了系统Hopf分岔的存在性;在第5节中,给出了数值模拟来验证理论结果的正确性;在第6部分,得出结论.
2 模型公式
本文基于SIQR恶意病毒传播常微分方程模型[12],考虑空间上的扩散效应,建立一类反应扩散SIQR恶意病毒传播动力学模型.假设SIQR模型中各状态节点分布密度具有归一化特征,即S(t)+I(t)+Q(t)+R(t)=1,则消去R态节点不会影响整体动力学行为,得到如下偏微分方程:
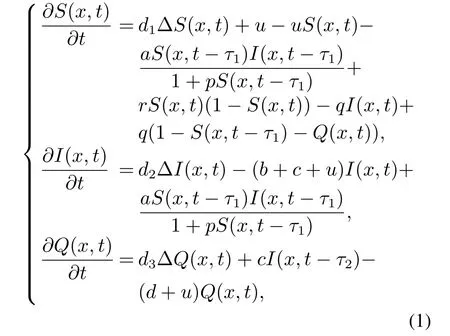
其遵循如下诺伊曼边界条件和初始条件:
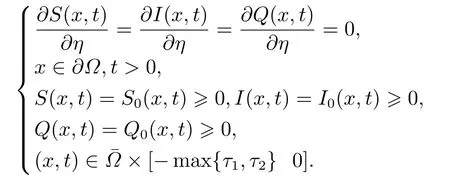
其中:S(x,t),I(x,t)和Q(x,t)分别表示易感染节点,感染节点和隔离节点在空间位置x和时间t上的分布密度;aS(x,t-τ1)I(x,t-τ1)/[1+pS(x,t-τ1)]表示实际感染率,a是感染率,p是预防效果系数;rS(x,t)(1-S(x,t))表示易感节点的logistic增长率,r是内禀增长率;τ1和τ2分别表示潜伏期和隔离期;c和q分别表示隔离率和转化率;b和d表示治愈率;u是接入率,-uS(x,t)中的u是退出率,这里接入率和退出率相等;d1,d2和d3分别表示易感染节点、感染节点和隔离节点空间扩散速率的扩散系数;初始条件S0(x,t),I0(x,t)和Q0(x,t)是非负连续函数.
注1诺伊曼边界条件:给出未知函数在边界外法线的方向导数.本文考虑了恶意病毒在一维空间中的扩散情况.Δ=∂2/∂x2表示一维空间中的拉普拉斯算子;Ω=(0,π)表示1个光滑边界∂Ω的有界域,η是∂Ω上向外的单位法向量.
考虑到CPS的工程意义,恶意病毒在CPS中传播时的潜伏期和隔离期实际为S态节点和I态节点转化的过程,在当代计算机的运算水平下,时间延迟的数值差异极小.不失一般性,假设τ1=τ2=τ,模型(1)变为


证毕.
3 时空动力学分析
基本再生数R0是判断恶意病毒能否在CPS中传播的阈值,具有重要的指示性.本文借助再生矩阵方法[12,14,16,18]计算模型(2)的基本再生数R0.当I(x,t)=0时,模型(2)中恶意病毒不存在.令模型(2)右端为0,不考虑扩散项易见模型(2)总存在无病毒平衡点E0=(1,0,0).忽略扩散和时滞,令X=(I Q)T,由模型(2)可知
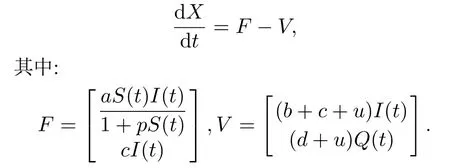
其在无病毒平衡点E0处的雅可比矩阵分别为
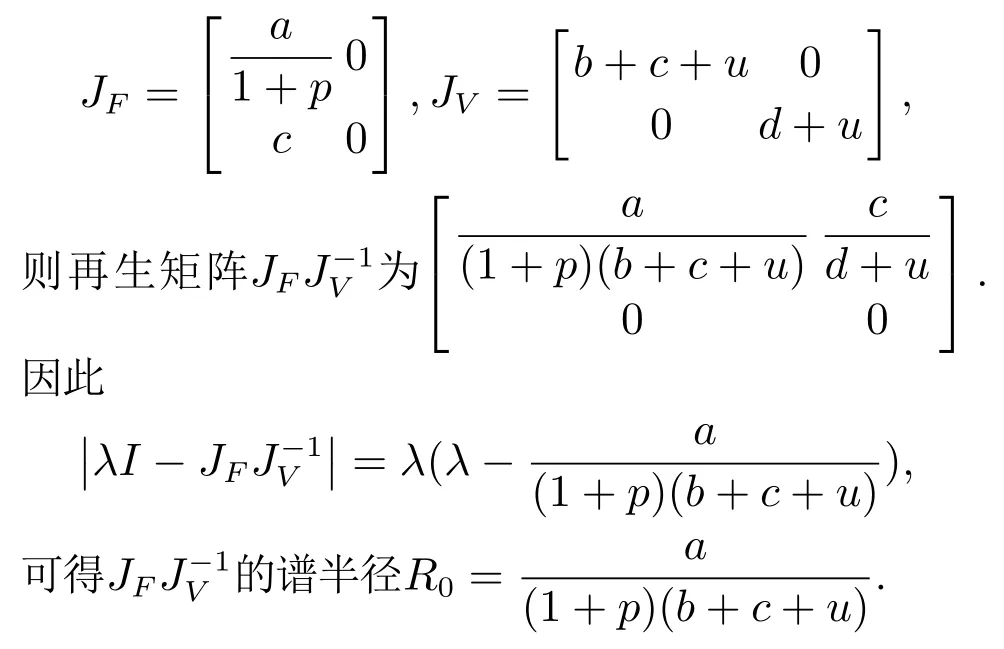
当微分方程右端为0时,模型(2)所示系统还具有1个地方病毒平衡点E*=(S*,I*,Q*),其中:
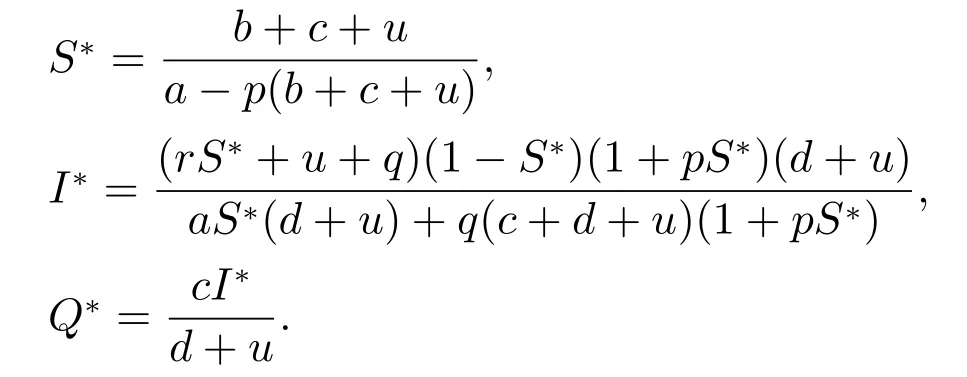
引理2如果R0=1,模型(2)具有无病毒平衡点E0;如果R0>1,模型(2)具有1个地方病毒平衡点E*.
证当R0=1时,有a=(1+p)(b+c+u).此时,S*=1,I*=0,Q*=0,表明地方病毒平衡点E*退化为无病毒平衡点E0;若R0>1,则易见0<S* <1,进而有I* >0,Q* >0.此时模型(2)具有1个地方病毒平衡点E*. 证毕.
令
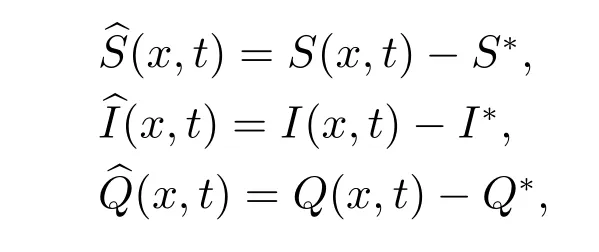
则模型(2)在平衡点E*处的雅可比矩阵为

所以,式(4)可以转化为以下形式:
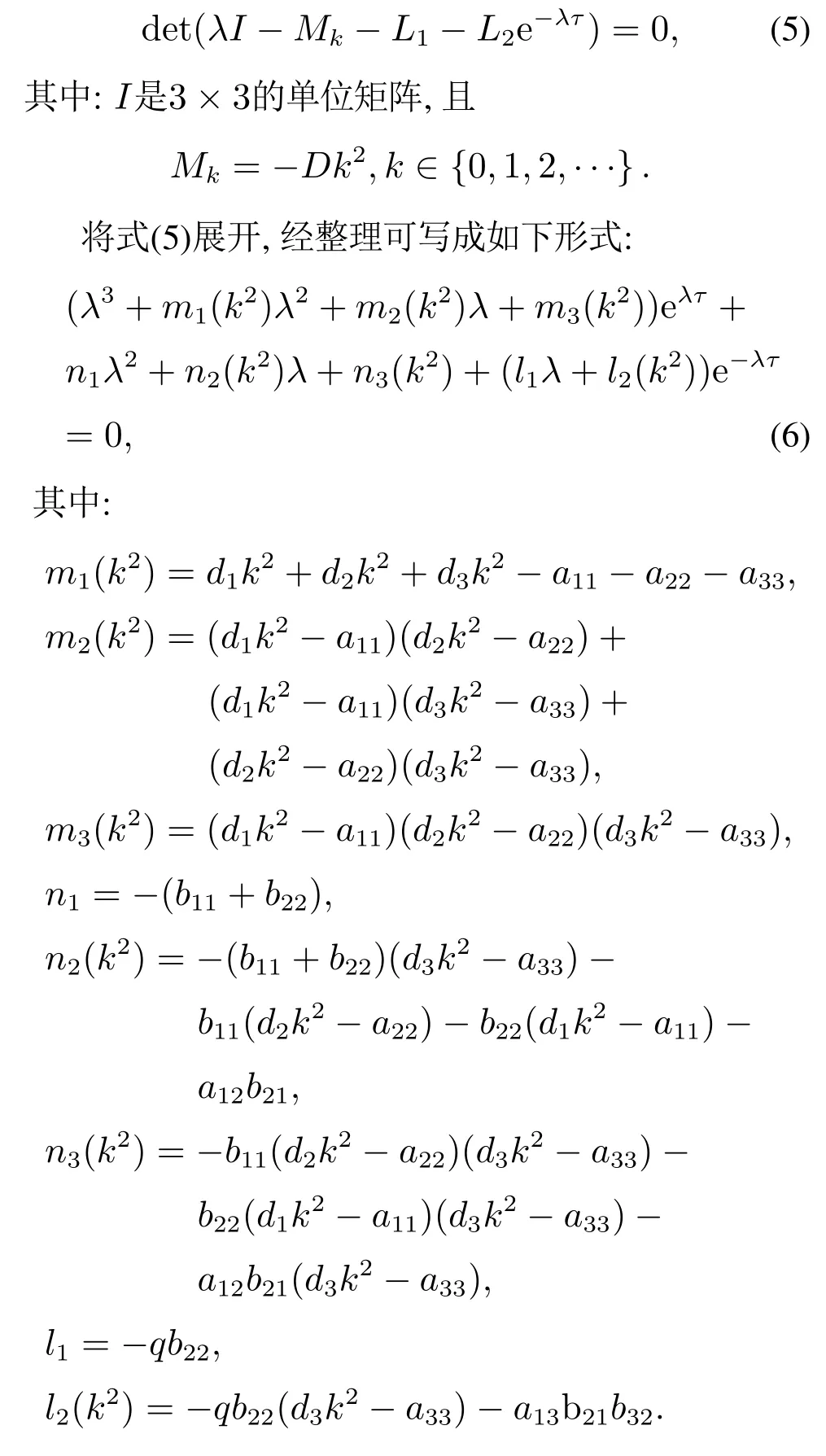
在接下来的两小节中,分析模型(2)的图灵不稳定性以及Hopf分岔的存在性.
3.1 图灵不稳定
图灵不稳定本质上是由扩散引起的不稳定现象.本节主要研究在无时滞情形下,模型(2)的图灵不稳定性.
当τ=0,di=0(i=1,2,3)时,特征方程(6)退化为
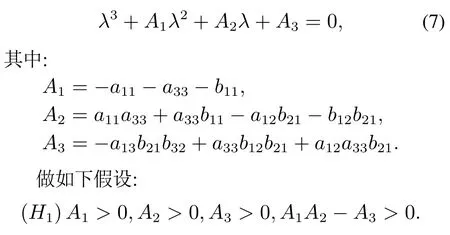
根据Routh-Hurwitz判据可知,如果(H1)成立,特征方程(7)的根均具有负实部.因此,模型(2)在无时滞和无扩散的情况下是局部渐近稳定的.

由引理1 可知,若A3>0,(H2)和(H3)成立,则f()=B3()<0.因此,方程g(λ;k0)=0至少有1个正根.
定理1假设R0>1,τ=0,且(H1)-(H3)成立.对于模型(2),本文有如下结论:
1)当di=0(i=1,2,3)时,地方病毒平衡点E*是局部渐近稳定的.
2)当di >0(i=1,2,3)时,地方病毒平衡点E*处发生图灵不稳定.
3.2 时滞诱导的Hopf分岔
在这一部分,考虑模型(2)的Hopf分岔.
当τ=0,di >0(i=1,2,3)时,模型(2)的特征方程为式(8).做如下假设:
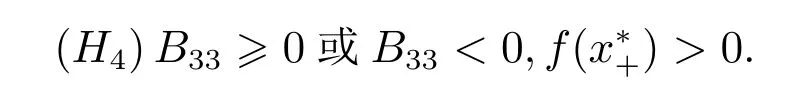
如果(H1)和(H4)成立,那么对于任意x>0,f(x)>0.因此B3(k2)>0.
通过计算得到
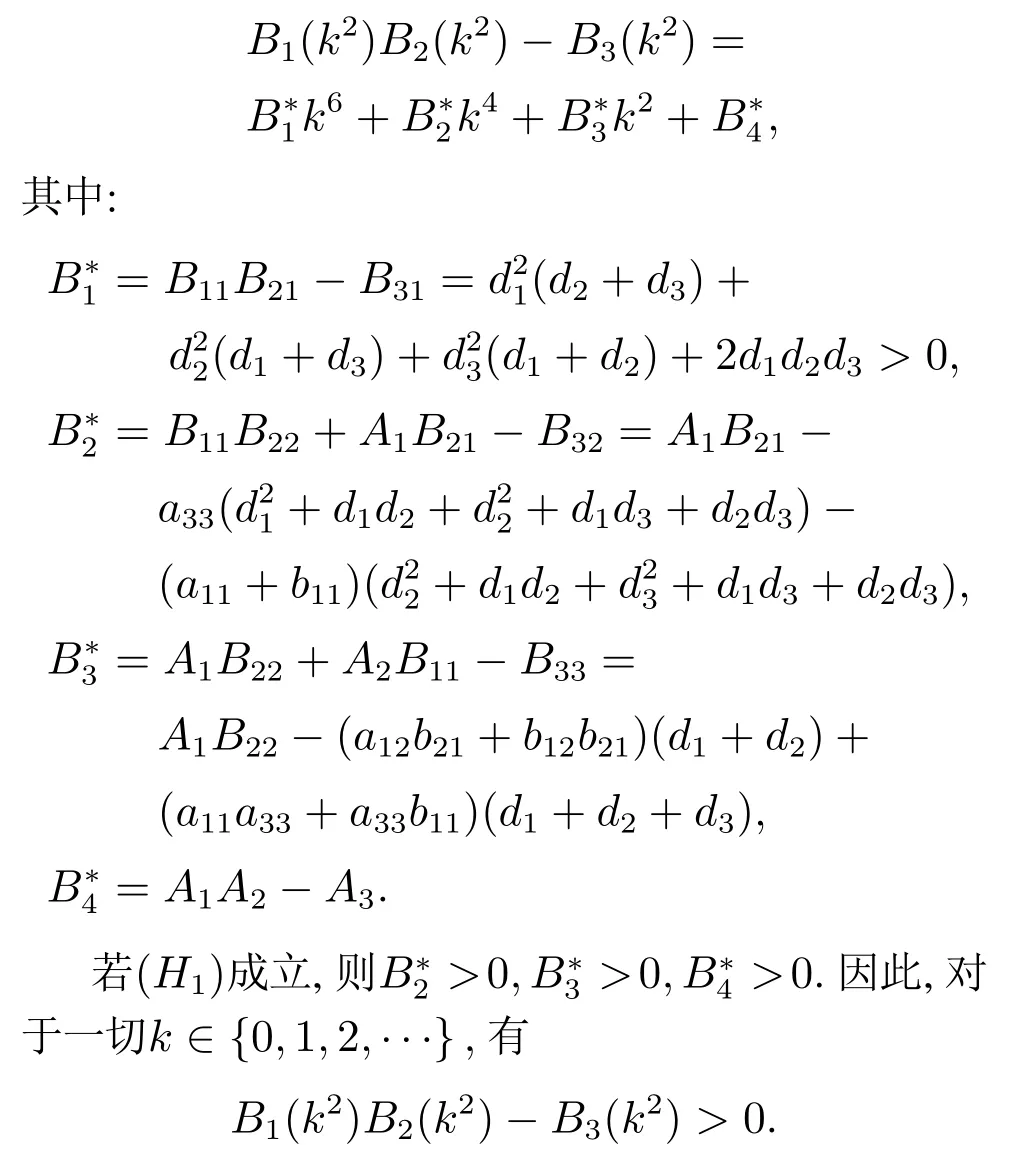
根据Routh-Hurwitz 判据,如果(H1)和(H4)成立,对于所有k ∈{0,1,2,···},方程(8)的根均具有负实部.因此,无时滞模型(2)的地方病毒平衡点E*是局部渐近稳定的.
当τ >0,di >0(i=1,2,3)时,假设特征方程(6)有纯虚根λ=iω(ω >0),将其代入式(6)并分离实部和虚部得
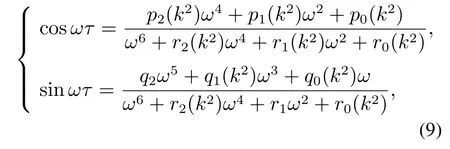


对方程(13)两边关于τ求导得

定理2假设R0>1,di>0(i=1,2,3),且(H1),(H5)-(H13)成立.对于模型(2),有如下结论:
1) 当τ ∈[0,τ0)时,地方病毒平衡点E*是局部渐近稳定的.
2) 当τ >τ0时,地方病毒平衡点E*是不稳定的,且当τ穿越τ0时,模型(2)在E*邻近发生Hopf分岔.
4 数值仿真
在这一节中,本文进行了一些数值模拟,以验证理论结果的正确性.模型(2)的参数选为
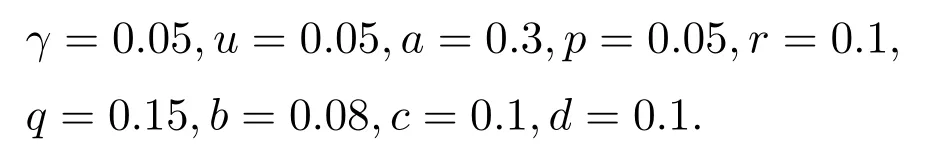
通过计算,得到R0=1.2422>1及地方病毒平衡点E*=(0.7972,0.1182,0.0788).
首先研究扩散对模型(2)稳定性的影响.选取初始条件为S(0,x)=0.7972+0.5 cosx,I(0,x)=0.1182+0.5 cosx,Q(0,x)=0.0788+0.5 cosx.当τ=0,d1=d2=d3=0时,可知(H1)成立.图1展现了模型(2)的地方病毒平衡点E*是局部渐近稳定的.

图1 模型(2)的地方病毒平衡点E*是局部渐近稳定的Fig.1 The local virus equilibrium E*of model(2)is locally asymptotically stable
当τ=0,d1=1,d2=0.001,d3=0.001时,易验证(H2)和(H3)成立.图2表明在扩散的影响下,模型(2)的地方病毒平衡点E*是不稳定的,这意味着图灵不稳定发生.
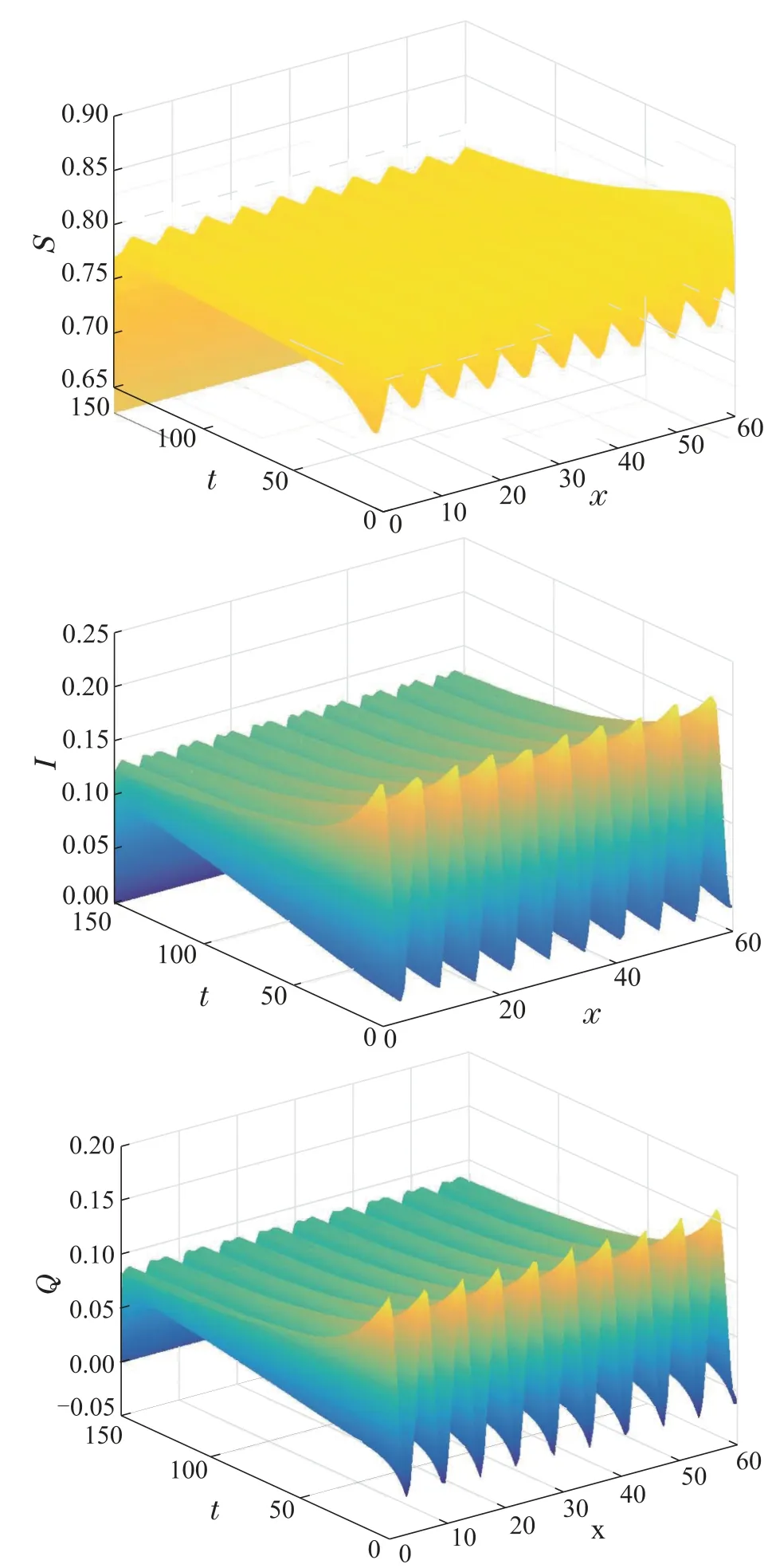
图2 模型(2)的地方病毒平衡点E*是不稳定的Fig.2 The local virus equilibrium E*of model(2)is unstable
然后,本文数值验证时滞诱发的Hopf分岔现象.令d1=d2=d3=1,并且初始条件为S(0,x)=0.8,I(0,x)=0.12,Q(0,x)=0.08.由式(9)和式(10)计算得ω0=0.0173,τ0=16.8662.此时,(H5)-(H13)均满足.
当τ=16<τ0=16.8662时,模型(2)的地方病毒平衡点E*是局部渐近稳定的,如图3所示;当τ=17>τ0=16.8662时,模型(2)的地方病毒平衡点E*变为不稳定,同时在E*邻近产生Hopf分岔,如图4所示.
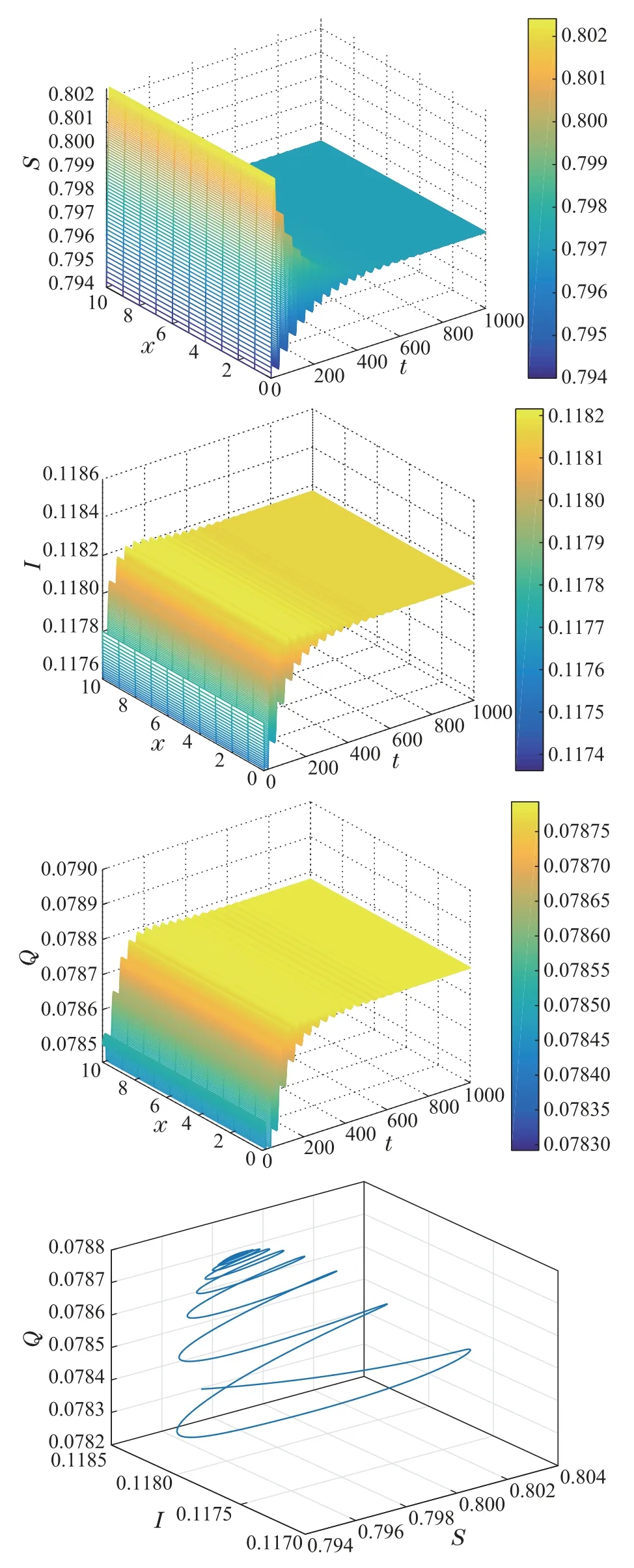
图3 当τ=16 <τ0=16.8662时,模型(2)的波形图以及相图Fig.3 Waveform plots of model (2) with τ=16 <τ0=16.8662 and the phase portrait
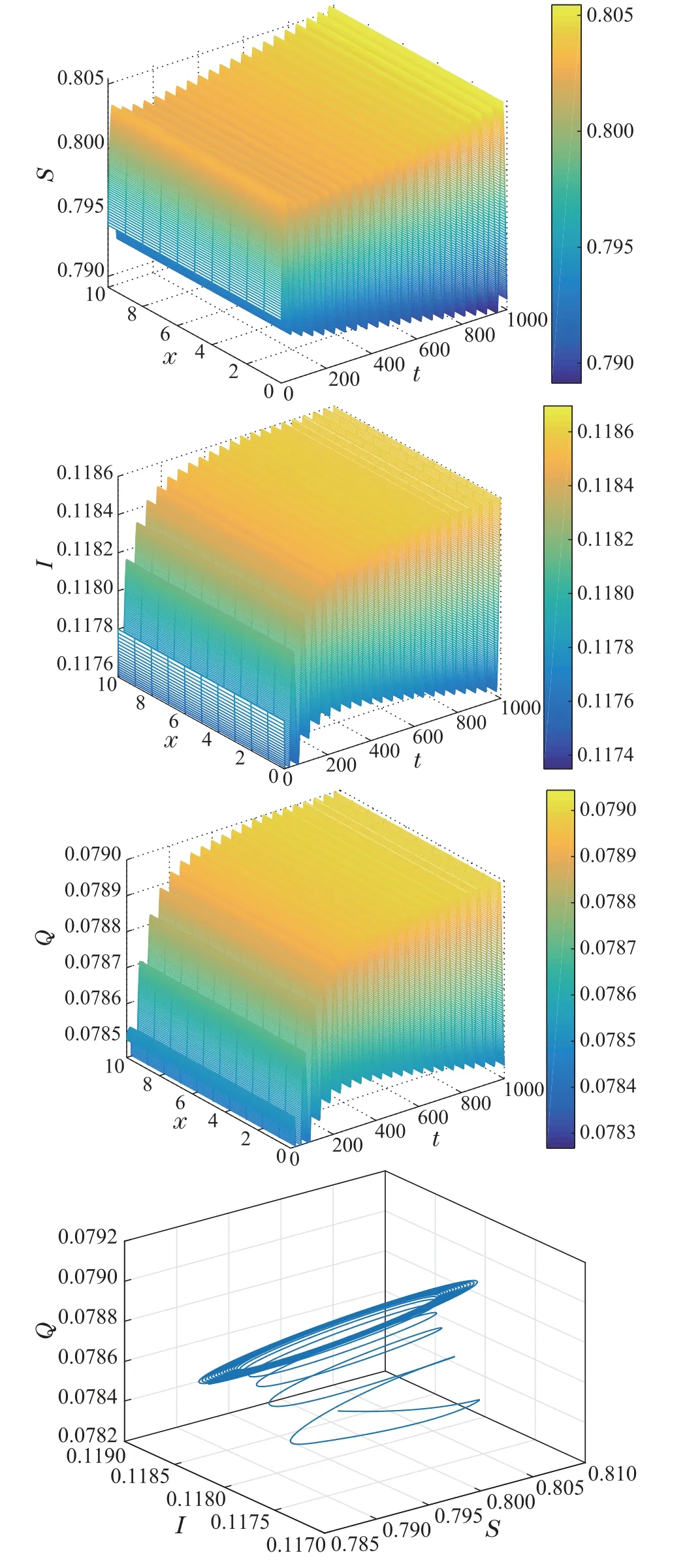
图4 当τ=17 >τ0=16.8662时,模型(2)的波形图以及相图Fig.4 Waveform plots of model(2)with τ=17 >τ0=16.8662 and the phase portrait
5 结论
本文通过引入扩散项,时滞,易感节点的logistic增长率,深化和完善了恶意病毒在CPS系统内部传播的时空动态演化研究.重点分析了扩散和时滞对CPS病毒传播模型动力学的影响.首先讨论了无时滞模型的稳定性.发现扩散项的引入会导致模型的不稳定,并严格证明了无时滞CPS病毒传播模型图灵不稳定的存在性.其次,本文分析了CPS病毒传播模型的Hopf分岔.选取时滞作为分岔参数,得到了Hopf分岔发生条件并给出了分岔阈值解析表达式.当时滞小于分岔阈值时,扩散的CPS病毒传播模型处于稳定状态;当时滞穿越分岔阈值时,模型失去稳定性并发生Hopf分岔.未来工作致力于分岔方向和分岔周期解稳定性的深入研究.
