量子力学力学量和表象理论“五步”计算方法的研究与应用*

伊厚会

(潍坊科技学院智能制造学院 山东 潍坊 262700)

刘慧

(滨州学院理学院 山东 滨州 256603)

量子力学是研究微观粒子运动规律的理论[1～3]，是我国工科类专业中一门非常重要的基础课程．通过对该课程的学习，有助于学生掌握量子力学的基本原理和方法，加深对微观世界中物理现象和微观粒子运动规律的理解和认识．量子力学涉及大量的公式推导和数学计算，课程教学对学生的数学、物理基础、逻辑思维能力与空间想象能力等都提出了极高的要求．多数教学往往只注重基础理论的讲解和数学公式的推导而忽略知识的应用和物理情境的构建，导致学生感到量子力学知识深奥难懂，影响了学生学习的积极主动性．特别是部分先修课程学习不深入，基础薄弱的学生，容易对量子力学这门课学产生恐惧心理，严重影响了教学质量和教学效果的提升．

在量子力学教学中，注重知识间的联系、思想方法的应用和知识网络的形成是非常必要的．力学量和表象理论是量子力学的重要内容[4，5]，文章针对这两部分内容，提出了“五步”计算方法．通过应用和举例，解决了量子力学教学内容的重点和难点．“五步”计算方法除有助于学生解决一系列计算问题之外，还有助于学生概念的理解、内容的掌握和知识体系的建立．文章重点介绍力学量和表象理论“五步”计算方法的内容和应用．

1 知识基础

力学量和表象理论是量子力学的重要内容，在学习这部分知识之前学生已初步掌握了量子力学的基本内容．它们主要有：

(1)微观粒子的运动状态用波函数Ψ(r,t)完全描述；

(2)|Ψ(r,t)|2表示在t时刻在r→r+dr中找到粒子的几率；

(3)波函数的变化满足薛定谔方程；

(4)量子力学中的力学量用厄米算符来表示；

(5)微观体系的状态用厄米算符的本征态(函数)表示；

(6)坐标、动量、角动量、能量算符本征方程的求解等．

2 力学量的计算

2.1 力学量的五步方法

在量子力学中用波函数Ψ(x,t)描写微观体系的状态．当微观体系的状态波函数Ψ(x,t)已知时，求力学量F，则按照“找、解、展、求、算”这5个步骤进行．具体如下.

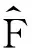
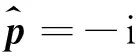
量子力学中，对应的动能算符为

在经典力学中，力学量角动量L=r×p，量子力学中，对应的角动量算符为

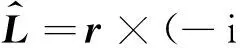
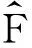
对于简并情况，通常也在本征子空间中取一组正交归一基．也可用力学量完全集算符来确定一组正交归一基．

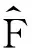
(4)“求”指求展开系数cn

|cn|2是力学量F的概率分布，其物理意义是力学量F的取值为λn的概率．

2.2 力学量实例

例如课本[1]例题求氢原子基态时，电子动量的概率分布．本题的条件是氢原子处于基态，即状态波函数

已知，需要求解的力学量是动量．对应的“找、解、展、求、算”的5个步骤分别如下所示.

(1)找动量算符

(2)解动量算符的本征方程是

-ih∇φp=pφp

动量算符的本征函数

(3)状态波函数

按照动量算符的本征函数

展开

(4)求展开系数c(p,t)

(5)计算|c(p,t)|2，即电子动量的概率分布为

同样如果已知状态波函数，计算L2，Lz，H等力学量，则需要找这些力学量分别对应算符，分别按照以上步骤求解计算即可．

2.3 力学量平均值的两步方法

由于

力学量F平均值的另一求法是利用公式

计算．在求解力学量平均值时，“找、解、展、求、算”五步可以简化并成“找、算”两步．

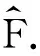
利用上式计算力学量时，步骤简单，公式简洁，便于学生记忆，但仅限于计算力学量的平均值．当利用“找、解、展、求、算”五步计算力学量时，除了可以求解力学量平均值之外，还可以得到力学量的概率分布．“五步”方法虽然步骤复杂，计算繁琐，但是有助于深刻理解量子力学中的相关概念，帮助学生建立量子力学观念和理论框架．

3 表象理论

3.1 表象理论的五步方法

在表象理论中，则按照“找、解、展、求、写”五步进行，前四步和求力学量的步骤相同，第五步直接把态和力学量写成矩阵形式即可．下面以Q表象为例，讨论态和力学量的具体形式.

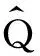
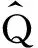
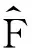
(5)“写”指波函数、算符在Q表象中写成矩阵形式，分别为

3.2 表象理论五步实例

下面分别以坐标表象、动量表象、能量表象为例，讨论态和力学量的五步计算方法．

3.2.1 坐标表象

式中x′为坐标算符的本征值，δ(x-x′)为属于本征值x′的本征函数．

(3)状态波函数按坐标算符的本征函数δ(x-x′)展开

(4)求系数ax′(t)和算符在坐标表象的矩阵元

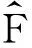
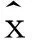
算符在坐标表象的矩阵表示是δ函数形式．在行列对应一致的前提下，则此δ函数前面的那部分就是此算符在坐标表象的算符表示．

(5)写出坐标表象中的波函数

在本征值为连续谱的情况下，由于列矩阵的行不可数，往往用矩阵元来表示列矩阵，因此，任意态Ψ(x,t)在坐标表象的表示就是Ψ(x′,t),就是任意态Ψ(x,t)本身．若某一态波函数是以坐标为自变量,那么它就是在坐标表象的表示,就是某一态以坐标本征函数展开的系数．

3.2.2 动量表象

(1)找动量算符

(2)解动量算符的本征方程

p为动量算符的本征值

为属于本征值p的本征函数．

(3)状态波函数按动量算符的本征函数展开

(4)求系数c(p,t)和算符在动量表象的矩阵元

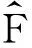
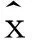
与坐标表象一样，算符在动量表象的矩阵表示也是δ函数形式．在行列对应一致的前提下，则此δ函数前面的那部分就是此算符在动量表象的算符表示．

(5)写出动量表象中的波函数

Ψ(x,t)是坐标表象中的波函数, 则c(p,t)就是在动量表象中表示的波函数．

3.2.3 能量表象

(1)找一维无限深势阱的哈密顿算符

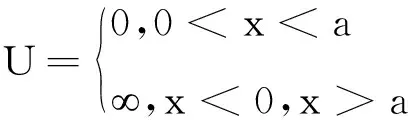
其中

为能量的本征值

为属于本征值En的本征函数．

(4)求展开系数cn和算符在能量表象的矩阵元

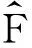
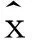
(5)写出能量表象中的波函数

4 结论

本文总结了量子力学力学量“找、解、展、求、算”和表象理论 “找、解、展、求、算、写”的五步计算方法．教学实践表明，“五步”计算方法使大量该类型题目的解题思路更加清晰明了．学生也较容易掌握量子力学的内容，建立完整的知识体系．在教学过程中注重知识间的联系和知识网络的形成是非常必要的．只有对教学内容深刻透彻理解，才能做到游刃有余、触类旁通．