基于多重降噪的改进SSA-LSSVM短期电力负荷预测模型
2022-11-07张树国
张树国,张 斌
(华北电力大学 经济管理系,河北 保定 071000)
0 引言
电力系统安全稳定运行是地区发展的前提。地区电力负荷的预测结果,可以为电网制定电力能源供应计划提供参考。短期电力负荷预测对保证电力系统高效平稳运行具有重要意义。
传统的电力负荷预测方法有趋势外推法[1]、回归分析法[2]、时间序列法[3]等。这些传统预测方法存在对数据的稳定性要求较高、难以准确预测短期电力负荷等问题。
随着研究的深入,粒子群(particle swarm optimization,PSO)[4]、支持向量机(support vector machine,SVM)[5]等机器学习方法被用于短期电力负荷预测。
文献[6]基于长短期记忆神经网络(long short term memory,LSTM)对短期电力负荷进行预测。由于LSTM在并行处理上存在劣势,所以当时间跨度较大时,LSTM的处理速度较慢。
文献[7]基于 SVM 对电网负荷进行了预测;但在历史数据量较大时,SVM难以实施。
文献[8]采用人工神经网络进行负荷预测。因所需参数较多,算法的预测准确性受到影响。
上述基于单一模型的电力负荷预测精度较低,不能够满足目前短期电力负荷预测对精度的要求;因此,需要对现有的方法进行深入研究。
为了提高预测模型的准确性,有相关研究采用组合预测模型来预测短期电力负荷。
文献[9]采用麻雀搜索算法(sparrow search algorithm,SSA)对LSTM模型进行优化。
文献[10]使用PSO对LSTM模型的参数进行寻优。
文献[11]基于卷积神经网络,对 LSTM 的参数进行优化,使模型能够更准确地预测短期电力负荷。
文献[12]用蚱蜢优化算法优化SVM的参数,并采用组合模型对电力负荷进行了预测。
文献[13]将天鹰优化算法(aquila optimizer,AO)与SVM集成,对智能电网的短期电力负荷进行了预测。
上述组合模型的特点是均采用优化算法对参数进行寻优;仍存在的问题是,优化算法迭代次数过少容易陷入局部最优,迭代次数过多计算速度又会下降,难以满足预测要求。
短期电力负荷数据具有波动性和随机性。如果直接将电力负荷数据用于预测,得到的预测结果难以达到预期精度。因此,在进行预测前,需要先对电力负荷数据进行处理,将复杂的电力负荷数据分解再进行重构,以在一定程度上消除随机数据的影响。
文献[14]基于集合经验模态分解(ensemble empirical mode decomposition,EEMD),用粒子群方法优化小波神经网络,最终实现了电力短期负荷预测。
文献[15]基于EEMD,采用粒子群算法优化了最小二乘支持向量机的参数。
文献[16]基于CEEMDAN及变分模式分解处理原始数据,采用鲸鱼优化算法优化支持向量机的参数,并将该混合模型用于电力负荷的预测。
文献[17]基于 CEEMDAN,利用卷积神经网络和门控循环单元建立组合模型,实现短期电力负荷预测。该数据分解策略虽然能够在一定程度上消除噪声对预测结果的影响,但分解后的一些数据分量仍较为复杂,难以直接用于预测。
基于以上分析,为提高短期预测模型的准确度,本文创新性地采用多重数据降噪的方法处理数据,并提出用改进SSA优化LSSVM参数的组合预测模型。首先,利用自适应小波阈值去噪方法对原始数据进行一次降噪处理;采用 CEEMDAN分解处理后的数据,再将分解后最复杂的分量采用 SVD进行二次降噪;利用三阶段优化的 SSA对LSSVM的参数进行寻优,建立组合预测模型,并利用组合预测模型对降噪后的各分量分别进行预测;最后,将各分量预测结果进行整合重构,得到短期电力负荷预测的最终结果。
1 数据处理方法
1.1 CEEMDAN原理
经验模态分解(empirical mode decomposition,EMD)是一种处理非平稳信号的方法,其特点是可以根据被分析信号自适应地产生固有模态函数[18]。
EMD方法的原理:将复杂的信号分解为有限个模态函数(intrinsic mode function,IMF)。分解得到的IMF包含了原始信号不同时间尺度的局部特征信息。
在EMD通过分解信号进而得到IMF的过程中,会出现模态混叠的现象:在同一个IMF分量中存在分布范围很宽却又不相同的信号,或者在不同的IMF分量中存在着尺度相近的信号。
模态混叠会使模型特征的提取和训练变得困难。为了解决这种问题,文献[19]提出了CEEMDAN方法——在每得到一阶IMF分量时,重新给残值加入白噪声并求IMF分量均值,然后逐次迭代。CEEMDAN方法能较好地解决模态混叠与虚假分量的问题。
CEEMDAN算法步骤如下。
(1)将高斯白噪声加入到原始信号中,得到新信号;对新信号进行EMD分解,得到第1阶段本征模态分量:
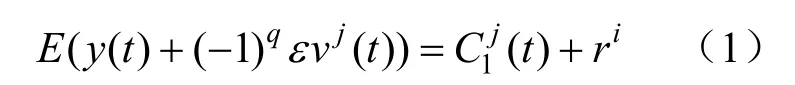
式中:y(t)为原始信号;ɛ为白噪声标准表;vj(t)为满足正态分布的高斯标准白信号;C1j(t)为第1阶段本征模态分量;ri为信号残差;E(y(t)+(-1)qɛvj(t))为新信号经EMD分解后的本征模态分量。
(2)对产生的N个模态分量做总体平均,得到经CEEMDAN分解的第1个IMF:

(3)去除第1个IMF,得到剩余信号r1(t):
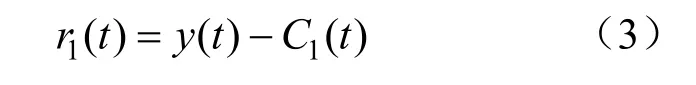
(4)在r1(t)中加入正负成对的高斯白噪声,得到新信号;对新信号进行EMD分解,得到第1阶段模态分量。由此得到经CEEMDAN分解的第2个IMF为:
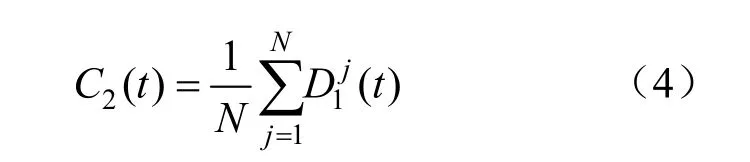
式中:D1j(t)为第1阶段模态分量。
(5)去除第2个IMF,得到剩余信号r2(t):
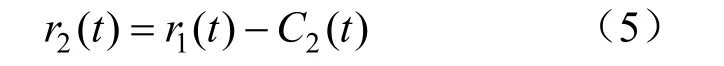
(6)重复上述步骤,直到剩余的残差信号为单调函数且不能继续分解,即完成分解过程。
最终得到K个IMF。原信号被分解为:
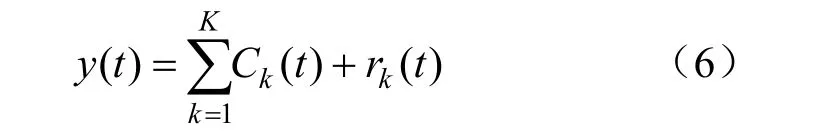
1.2 自适应小波阈值去噪原理
小波阈值去噪的思想是:首先将信号进行小波变换分解。分解后,信号的小波系数较大,噪声的小波系数较小。通过设定合适的阈值剔除噪声,从而达到信号去噪的目的[20]。
通常将小波阈值去噪分为软阈值法和硬阈值法2类。
硬阈值降噪法:
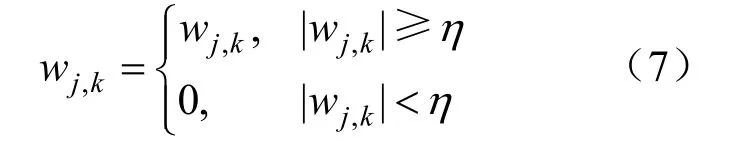
式中:wj,k为小波系数;η为阈值函数。
软阈值降噪法:
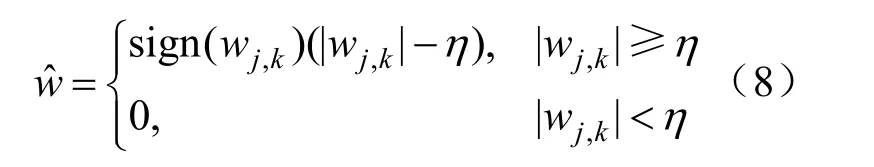
本文结合软阈值降噪法和硬阈值降噪法的优点,采用一种自适应的阈值函数:
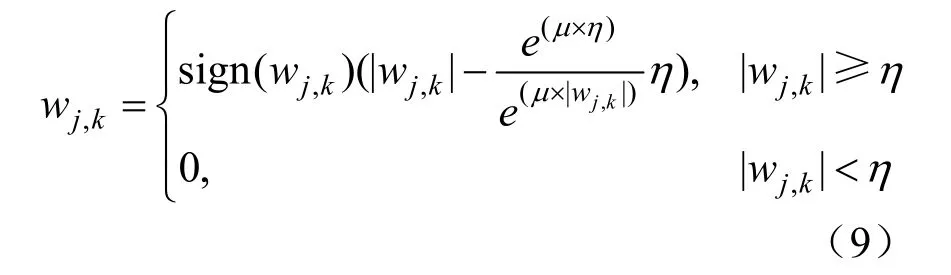
式中:μ为动态调节因子。
当μ值趋于0时,阈值函数变为软阈值函数;当μ值趋于无穷时,阈值函数变为硬阈值函数。
1.3 SVD原理
SVD是一种分解矩阵的方法,常用于数据压缩、数据去噪[21]。
SVD的原理如下:
对实矩阵 A ∈ Rm×n,必定存在一个m阶正交矩阵和一个 n阶正交矩阵,使得 A = UΣ VT。Σ为矩阵A的全部非零奇异值。Σ的前几个值较大,包含着矩阵A的大部分信息;Σ其余的值较小,代表着矩阵的噪音。去除代表噪音的奇异值即可以达到去除噪声的作用。
将所测的时间序列信号按每n个点截取m段的连续截取方式构造矩阵,得到的新矩阵如下:

式中:m和n大于1。
2 预测方法
2.1 SSA原理
SSA是一种新型的智能优化算法,其通过模拟麻雀的觅食和反捕食行为来进行局部和全局搜索,其寻优能力强、收敛速度快[22]。
SSA种群中,含有发现者、加入者和侦察者3种类型的麻雀。具有良好适应度的个体为发现者,负责寻找食物并为整个种群提供觅食方向。当侦察者发现捕食者后会发出信号,麻雀种群会做出反捕食行为。
SSA算法步骤如下。
由n只麻雀组成的麻雀种群X可描述为:

式中:d为优化问题的变量维数。
(1)初始化麻雀种群位置和适应度。
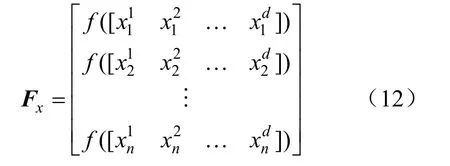
式中:f为适应度值。
(2)排序得出当前最优个体位置和最佳适应度。
(3)更新发现者位置。
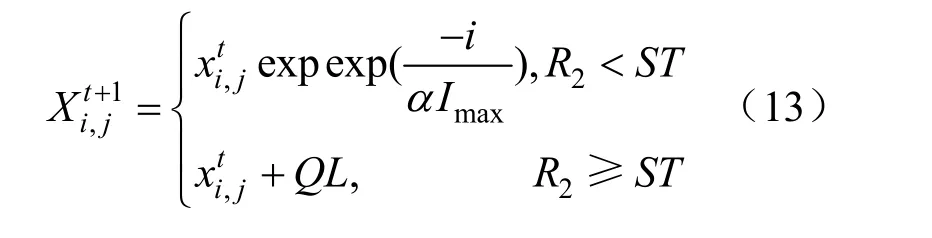

(6)计算适应度,更新麻雀位置。
(7)判断停止条件:如果满足,则输出最优参数;如果不满足,则重复执行步骤(2)—(6)。
2.2 ISSA原理
麻雀搜索算法的缺点是:初始种群位置单一、全局搜索能力差、容易陷入局部最优、算法的精确度不足。
针对以上缺陷,本文从3个方面对麻雀搜索算法进行改进。
(1)初始化种群阶段
麻雀搜索算法的初始种群位置决定了算法的寻优能力。本文引入Piecewise映射对麻雀搜索的初始位置进行映射:
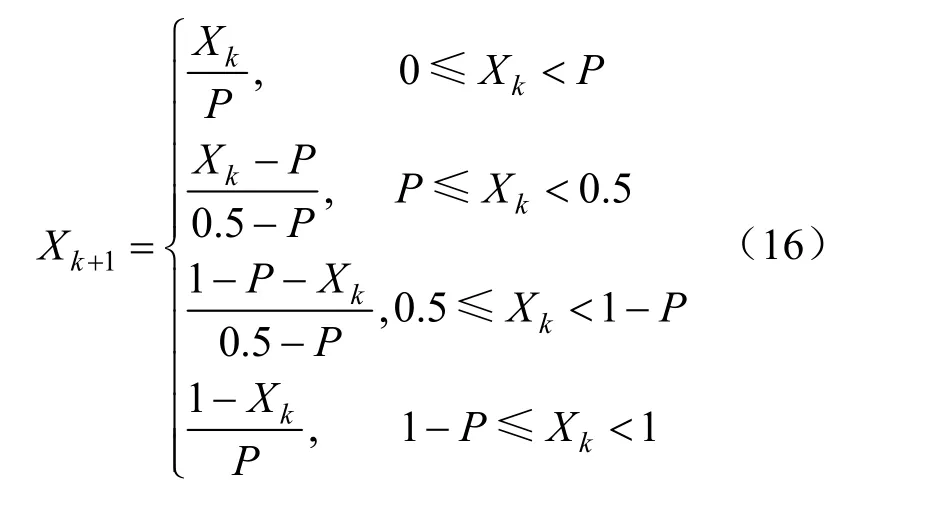
式中:P、X的取值范围是0~1。
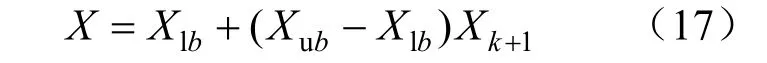
式中:Xlb为每个维度的下限;Xub为每个维度的上限。
采用公式(17)得到的X为Piecewise映射的初始种群。该操作提高了麻雀搜索初始种群分布的多样性。
精英反向学习可以保证种群的精英性。
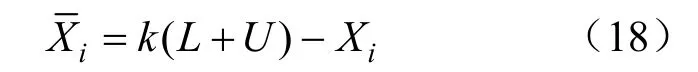
式中:Xi为个体当前的信息;L和U分别为可行解的最小值和最大值;k是0~1的随机数。
种群初始化的优化流程为:分别计算由Piece-wise映射和精英反向学习获得的种群适应度值;在对适应度值排序后,选取较优个体作为种群的初始个体。
(2)寻优阶段
麻雀搜索算法的全局和局部寻优能力不强,容易陷入局部最优情况。
本文采用加入动态自适应权重ω的方式,优化算法的全局搜索和局部开发能力。
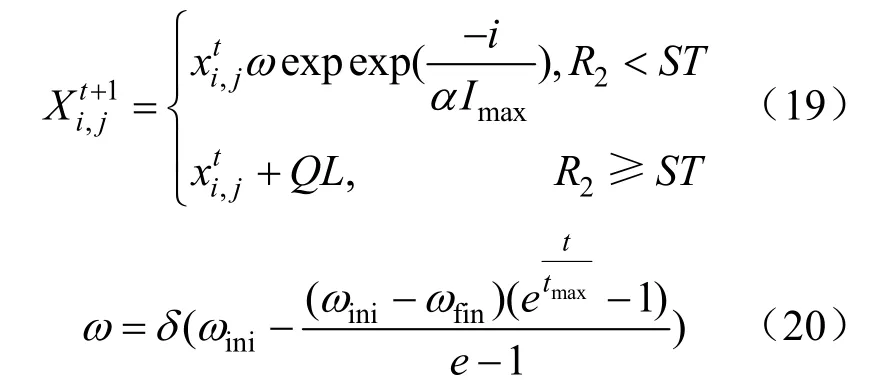
式中:ωini为初始权重;ωfin为最终权重;δ为0~1均匀分布的随机数。
在算法搜索前期,权重ω较大,发现者能够充分进行全局搜索;到算法搜索后期,权重ω减小,以有利于算法进行局部搜索。
均匀分布的δ使权重ω实现动态变化,加快算法的收敛。
(3)最优麻雀阶段
若算法中的最优麻雀达到适应度值时搜索停止,则结果容易陷入局部最优。本文采用随机游走算法对最优麻雀进行扰动,以提高搜索性能。
随机游走方法的过程为
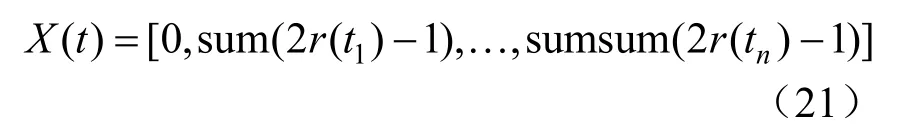
式中:X(t)为随机游走的步数集;sum为计算累加和函数;t为随机游走步数。

式中:r为0~1的随机数。
为了确保麻雀游走范围可行,需要对麻雀位置进行归一化。

式中:ai为随机游走的最小值;bi为随机游走的最大值;为变量在第t次迭代的最小值;为变量在第t次迭代的最大值。
2.3 LSSVM原理
LSSVM 可以用来解决模式分类和函数估计等问题。LSSVM使用最小二乘线性系统作为损失函数,代替了传统 SVM 方法采用的二次规划方法,从而简化了计算[23]。

3 模型构建
3.1 ISSA-LSSVM优化模型构建
影响LSSVM算法的2个重要参数是惩罚参数和核函数参数。惩罚参数过小,会使模型的预测精度减;惩罚参数过大时会使模型变复杂,计算速度变慢。核函数参数过大会导致支持向量减少,过小则会使模型过饱和。
本文采用 ISSA算法对惩罚参数和核函数参数进行优化,以提高 LSSVM 预测的准确性。优化过程如图1所示。

图1 ISSA优化LSSVM流程图Fig. 1 Flow chart of LSSVM optimization by ISSA
3.2 多重降噪ISSA-LSSVM模型建立
本模型的预测流程如图2所示。首先将原始数据用自适应小波阈值降噪,然后采用CEEMDAN分解得到IMF分量和Res分量;将较复杂的IMF分量提取出来,进行SVD降噪;将CEEMDAN分解得到的剩余分量和经过 SVD降噪得到的分量用ISSA-LSSVM模型进行预测;将所有分量的预测结果进行整合,得到预测结果。
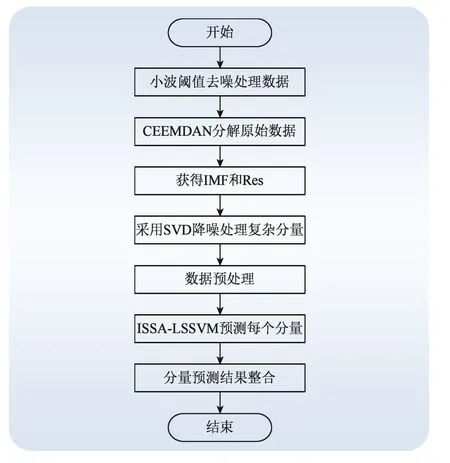
图2 多重降噪优化ISSA-LSSVM流程图Fig. 2 Flow chart of multiple noise reduction for ISSA-LSSVM optimization
4 实例仿真
4.1 数据降噪处理
本文以某地区2018年1月1日到2019年12月31日的日电力负荷数据为算例。将前529条数据作为训练集,将后200条数据作为测试集。
首先对原始数据进行小波阈值去噪处理。分别采用软阈值、硬阈值和自适应阈值对原始数据进行去噪。去噪结果如图3所示。相关指标对比结果如表1所示。

表1 小波阈值去噪指标Tab. 1 Wavelet threshold denoising index
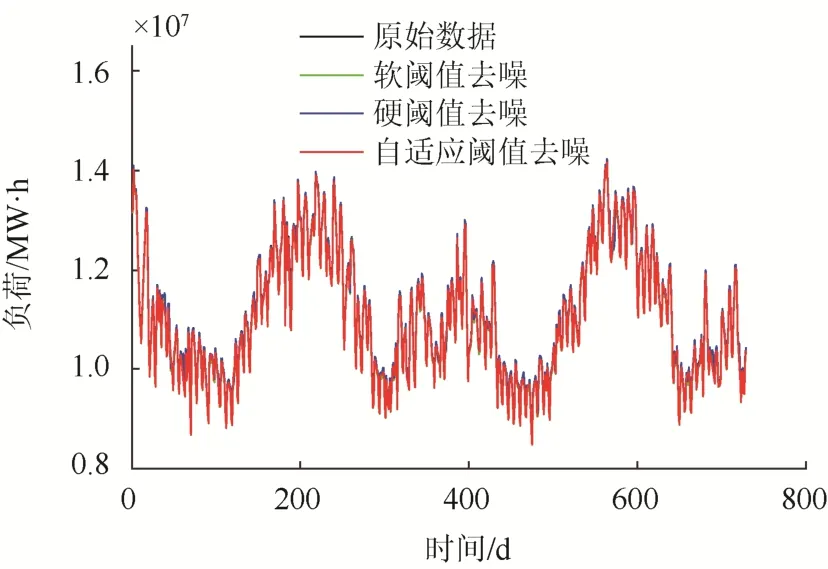
图3 小波阈值去噪结果Fig. 3 Wavelet threshold denoising results
由表1数据可以看出:采用自适应阈值去噪方法得到的SNR值为28.22,分别比硬阈值和软阈值去噪方法提升30.17%和21.74%;MSE值较硬阈值和软阈值去噪方法降低49.79%和40.68%。该结果表明,采用自适应去噪方法的效果较好。
对采用自适应去噪方法处理后的数据进行CEEMDAN分解,分解结果如图4所示。从图4可以看出,CEEMDAN分解后的IMF1较复杂。采用SVD方法对IMF1进行降噪处理,处理结果如图 5所示。从图5可以看出,去噪后的IMF1较为平缓,适合进行预测。
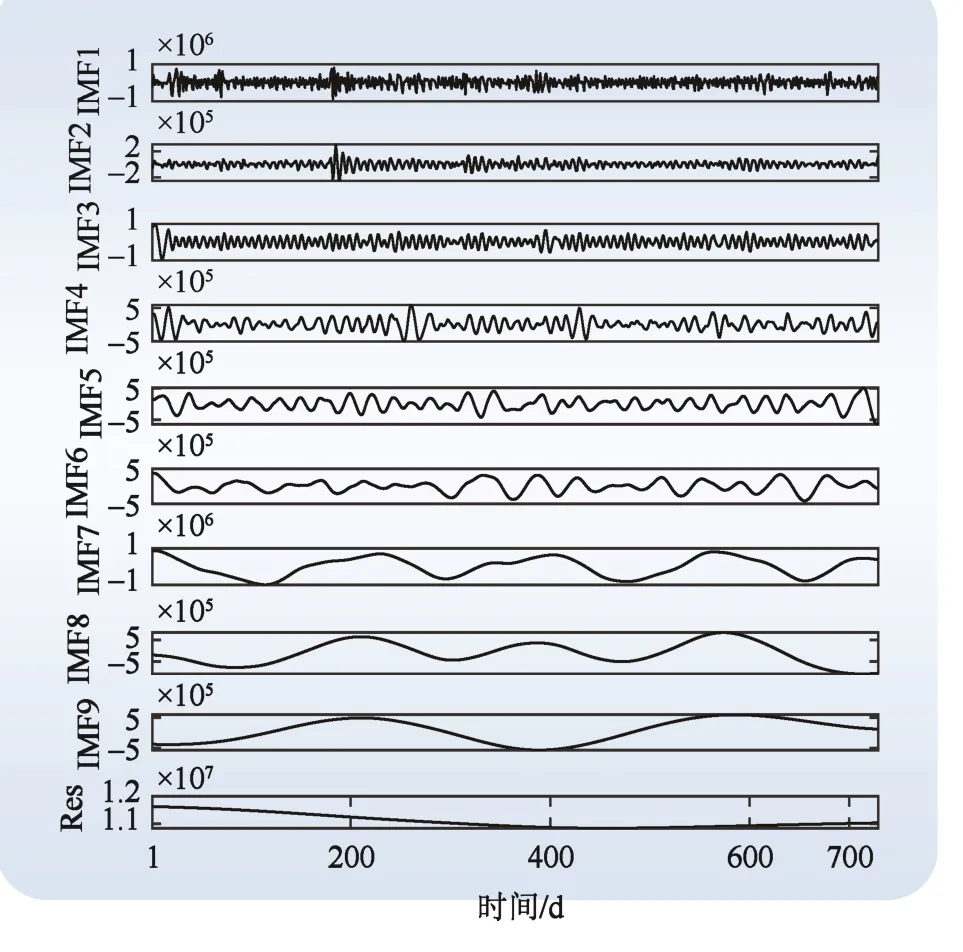
图4 CEEMDAN分解结果Fig. 4 CEEMDAN decomposition results

图5 SVD降噪结果Fig. 5 SVD noise reduction results
4.2 数据预处理和评价指标
为了提高预测精度,首先对负荷数据进行归一化处理

式中:u为初始负荷值;umax为最大负荷值;umin为最小负荷值。
为了量化预测模型的精度,本文采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)作为评估指标。
4.3 ISSA-LSSVM预测
为了验证本文所提出的ISSA-LSSVM的预测模型的优越性,将其与AO-LSSVM、PSO-LSSVM、ISSA-LSSVM预测模型进行对比。
设定:各算法种群的数目均为20,最大迭代次数为 100。LSSVM 的 gam参数取值范围为[0.1,1000],sig2参数的取值范围为[0.1,100]。
各优化算法的迭代过程如图6所示。
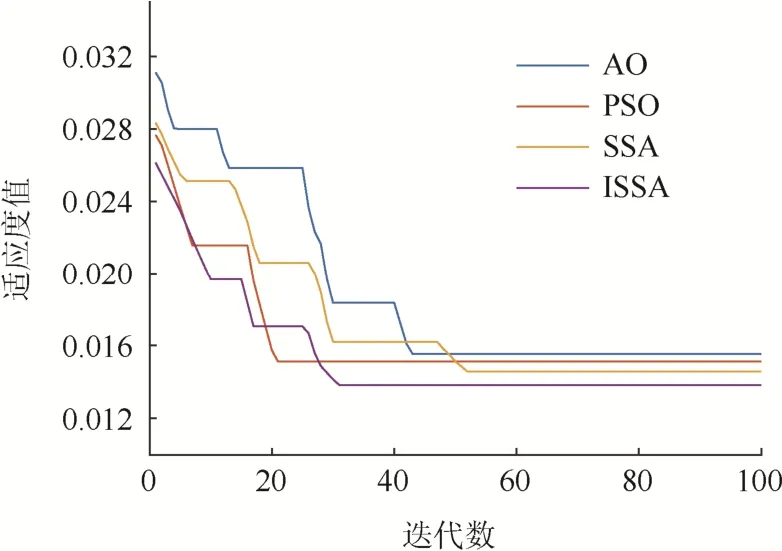
图6 各优化算法迭代过程Fig. 6 Iteration process of each optimization algorithm
从图6可以看出:AO算法的迭代速度较慢,适应度值也较大,出现了陷入局部最优的情况。PSO算法的迭代速度较快,但是适应度值较大,即寻优效果较差。SSA算法的寻优效果较好,但是迭代速度过慢,容易陷入局部最优。本文提出的 ISSA算法能够在保证适应度值足够小的情况下拥有较快迭代速度,这说明ISSA可以很快跳出局部最优情况。与SSA算法对比的结果说明,ISSA有助于提升迭代速度、提高预测准确度。
各优化算法下LSSVM的参数如表2所示。预测结果如图7所示。预测结果评价如表3所示。
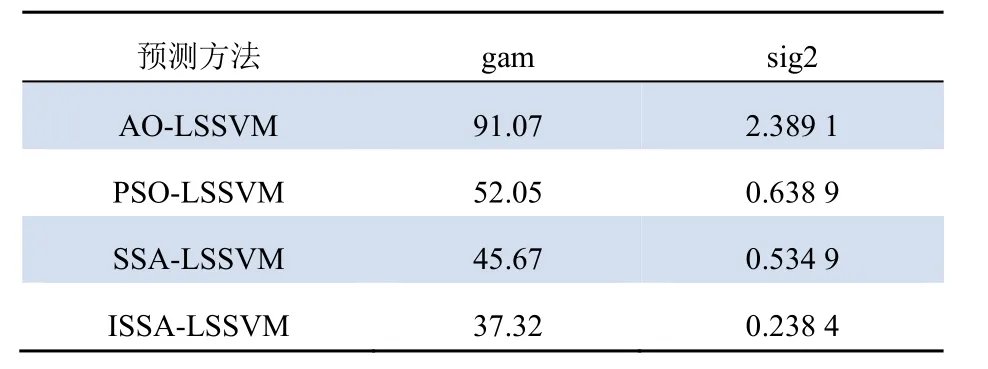
表2 各优化算法得到的LSSVM参数Tab. 2 LSSVM parameters obtained by each optimization algorithm
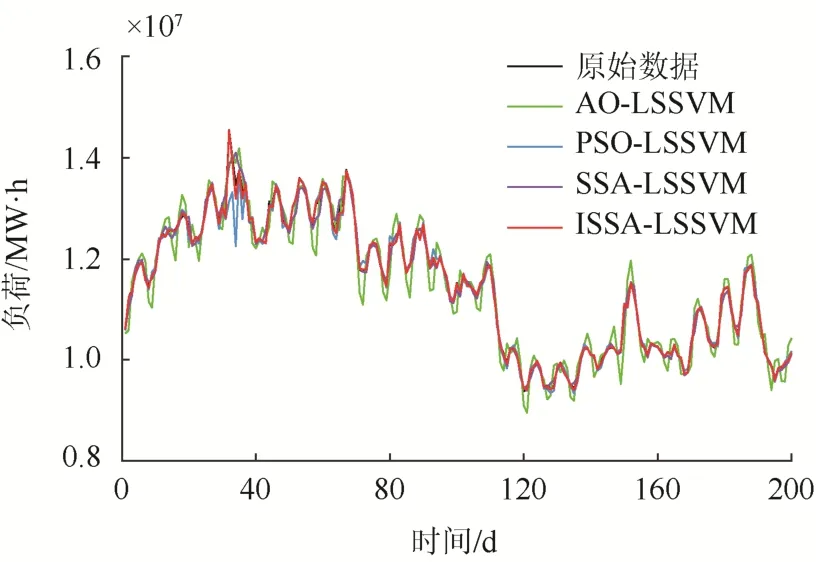
图7 各优化算法预测结果Fig. 7 Prediction results of each optimization algorithm
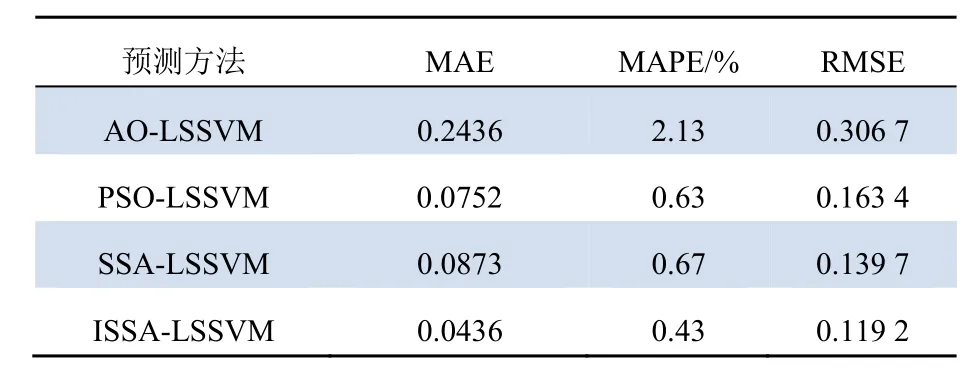
表3 各优化算法预测结果指标Tab. 3 Prediction result index of each optimization algorithm 106MW·h
考察图7、表3可知:在未对SSA算法进行优化时,SSA-LSSVM算法的MAE、MAPE值均比PSO-LSSVM算法大,这说明SSA-LSSVM的预测效果比PSO预测效果差;在对SSA算法进行优化后,ISSA-LSSVM预测模型相比SSA-LSSVM,MAE值降低 50.06%,MAPE值降低 35.82%,RMSE值降低14.67%。这说明,优化方法有效提高了SSA算法的准确性,也再次说明多策略改进SSA算法的有效性。
4.4 多重降噪优化ISSA-LSSVM预测
为了验证多重降噪优化的有效性,分别对经CEEMDAN分解和经多重降噪优化后的数据进行ISSA-LSSVM预测,预测结果如图8所示。
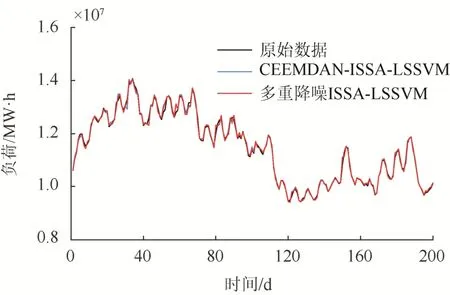
图8 多重降噪的预测效果对比Fig. 8 Comparison of prediction effects of multiple noise reduction
由图8可以看出,在将数据进行多重降噪优化后,预测结果比经CEEMDAN分解后的预测结果更加准确。
2种算法优化结果的评价指标如表4所示。由表4可以看出,与单纯采用CEEMDAN分解数据的方法相比,多重降噪优化后预测结果的 MAE值降低7.07%,MAPE值降低15.79%,RMSE的值降低15.95%。这说明,多重降噪后的预测效果比单纯采用CEEMDAN分解的预测效果好。

表4 各预测模型指标Tab. 4 Indicators of each prediction model 106MW·h
多重降噪优化ISSA-LSSVM的预测结果与表3中ISSA-LSSVM预测结果相比,MAE值降低了18.58%,MAPE值降低了25.58%,RMSE值降低了31.04%——说明将数据进行多重降噪优化能够提升预测的准确性。
5 结论
本文基于多重降噪方法,将多策略优化的ISSA-LSSVM 组合模型应用到短期电力负荷预测中,得到以下结论:
(1)在将原始数据 CEEMDAN分解前采用自适应小波阈值降噪,再将分解得到的复杂 IMF进行SVD降噪,最后将处理后的数据用于电力负荷预测。这种方法可以提高预测模型的准确性。
(2)使用多策略改进的ISSA算法对LSSVM的惩罚参数和核参数进行优化,能够有效提高LSSVM模型的预测效果。
