灌区末级渠道量水设施水流水力特性数值模拟

2022-11-07王立新路新川

节水灌溉 2022年10期

李超，王立新，肖宇，路新川

（1.内蒙古农业大学，呼和浩特 010018；2.内蒙古大学，呼和浩特 010021；3.黄河万家寨水利枢纽有限公司，太原 030002）

0 引言

灌区量水是合理配置水资源的基础，是推进节水农业发展的重要手段。建设现代化节水灌区急切需要研发精度高、计算简便、便于施工且造价低的量水设备。为提高量水设施的适用性和精度，国内外学者已经研发出针对各类渠道不同形式的量水槽、量水堰达百种。尤其是巴歇尔和无喉道量水槽因水头损失小，抗淤堵性能好、精度高等优点而在灌区内广泛应用[1]。量水槽的原理是通过在量水槽内形成临界流，从而建立上游水位与流量的单一函数关系，利用量测上游水位推求渠道流量变化[2]。但在实际工程应用中，由于各量水槽结构形式及水流流态、流量范围、测流精度等差异较大，研究不同形式量水槽的水流流态并选择精度高、水头损失小的量水槽对农业节水和水资源优化配置有重要的意义。

针对不同形式的量水槽广大学者开展了大量的室内试验和野外观测。随着数值模拟技术的不断发展，应用计算流体力学（Computational Fluid Dynamics,CFD）的方法能够较为精准高效地模拟量水设施水流水力参数及流态分布，并使模拟流体运动轨迹、流速、压强等物理量可视化呈现[3-7]。根据不同的渠道形状及流量量测特征要求，以模型试验为基础，结合数值模拟方法，分析量水槽内水面线、流态及弗劳德数等相关参数，探索各种流量和渠道断面下机翼形、长喉道等不同结构形式量水槽的测流公式[8-11]。尤其是巴歇尔槽自1922年被Parshall 在文丘里量水槽基础上改进设计出来后，很多学者开展了巴歇尔槽的水力特性、水位～流量关系及水头损失方面的研究[12,13]。向德华[14]采用实验结合数值模拟的方法分析了槽底为水平的类巴歇尔槽在不同流量下的流速、压力及相分布规律，为类巴歇尔槽的设计提供了依据。许虎[15]通过数值模拟方法分析了巴歇尔槽不同进口连接段形式对水头损失、水面线、测流误差、流速及压强影响的变化情况，指出采取进口连接段过渡的巴歇尔槽相比无连接段过渡水流流线更平缓，水头损失更小，且来流量越大，测流精度相对误差越小。对于上下游条件变幅较大的渠道，采用断面量水法或均匀流公式存在较大误差，白静[16]基于实时测定2 个断面的水位变化，通过求解水动力学模型而得到断面的流量。相比于求解水动力学方程，采用量水槽进行流量测定更加快捷、方便和简单，但各种量水槽结构类型不同，对于量测的流量变化范围灵敏度不同。同时，在量水槽的槽型选择时还应考虑有效水头、最大淹没度、水头损失等因素。需要细致、微观地分析不同类型量水槽内部的水流水力特性，探究不同流量情况下各量水槽测量精度的敏感性。同时，综合考虑影响流态、水头损失等方面的因素，针对不同测流工况选择精度高、水头损失小的量水槽，从而保障渠道高效输水和数字化、智慧化灌区建设。

本研究采用数值模拟方法分别模拟了不同流量下巴歇尔槽和长喉道槽的水流水力特性，分析各流量下模拟精度、水面线、流速、流态、流线、水头损失的变化及影响因素，为不同情况下灌区末级渠道量水设施的选型和应用提供理论指导。

1 材料与方法

1.1 物理结构模型

根据《灌溉渠道系统量水规范》（GB∕T21303—2017）中的规定[17]，采用标准设计尺寸建立巴歇尔槽和长喉道槽的三维物理模型。巴歇尔槽由进口段、收缩段、喉道段、扩散段、出口段及上下游水尺组成。其中，各段长度依次为2.243 m、1.325 m、0.6 m、0.9 m 和2.176 m，各段坡降依次为-0.25、0、0.375、-0.167 和0.143，喉道宽度为0.25 m。长喉道槽由进口段、收缩段、喉道段、扩散段组成。其中，各段长度依次为1.0 m、0.9 m、0.8 m 和1.3 m，喉道为矩形断面，底槛高度为0.4 m，喉道宽度为0.7 m。巴歇尔槽和长喉道槽的上、下游渠道均为梯形断面，渠道底宽为0.4 m，边坡系数m=0.414，上游段长度为20 m，下游段长度为15 m，从而保证水流有足够的行进长度，以供紊流充分发展。应用GAMBIT软件进行物理建模，构建的巴歇尔槽和长喉道槽三维结构如图1 和图2所示。

图1 巴歇尔槽几何模型Fig.1 Geometric model of Parshall flume

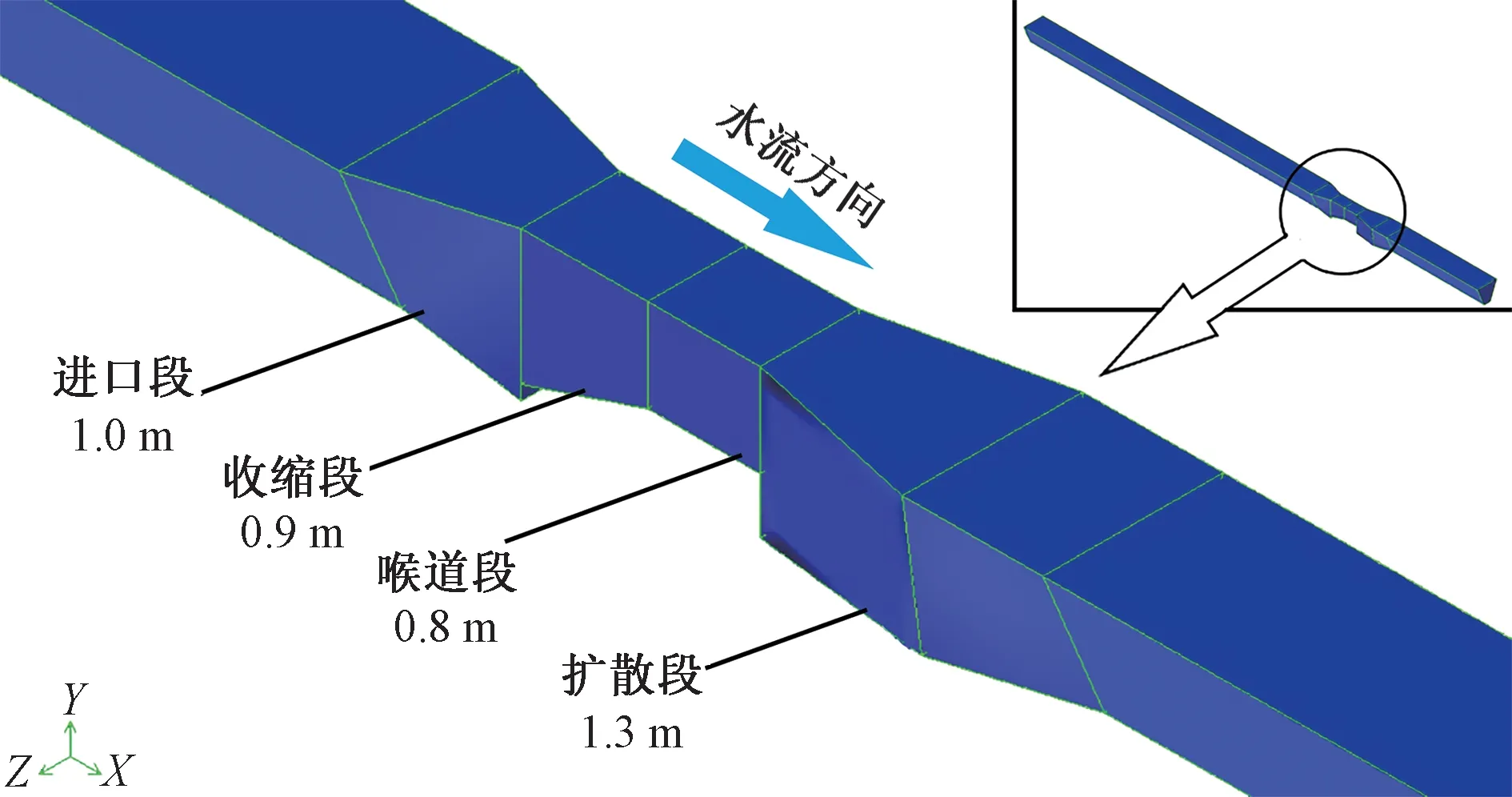
图2 长喉道槽几何模型Fig.2 Geometric model of long-throated flume

1.2 模型控制方程

标准k-ε湍流模型[18]的湍动能k和耗散率ε的输运方程分别为：

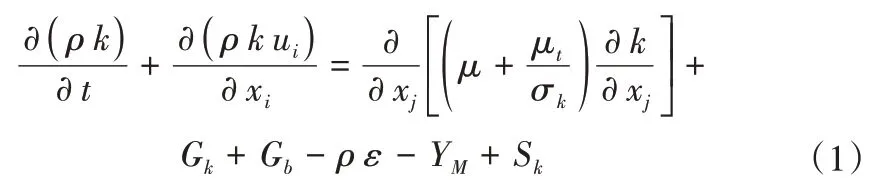
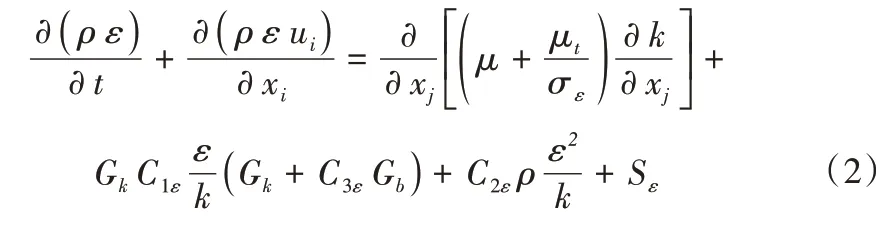
式中：ρ为流体密度，kg∕m³；ui为速度分量，m∕s；t为时间，s；xi、xj分别为i和j流向分量，m；μ为动力黏度，Pa·s；μt为涡黏性系数，μt=ρ Cμ k2∕ε；Gk为时均速度梯度引起的紊动能k的产生项，Gb为浮力引起的紊动能k的产生项，对于不可压缩流体，Gb=0；YM为可压缩紊流中的脉动扩张项，YM= 2ρ ε M2t；C1ε为模型系数，取1.44；C2ε为模型系数，取1.92；C3ε为经验常数，当主流方向与重力方向平行时，有C3ε=1，而当主流方向与重力方向垂直时，则有C3ε=0；k为湍动能，m2∕s2；ε为湍动能耗散率，m2∕s3；σk为湍动能对应的Prandtl 数，取1.0；σε为湍动能耗散率对应的Prandtl数，取1.3；Sk、Sε为分别为用户定义的源项。

明渠水流属于含有自由表面的水流流动，涉及到气-液2相流，本文采用处理互不交融交界面的VOF （Volume of Fluent）模型来模拟自由表面。VOF 模型中假设水和空气具有相同的速度，在每一个网格单元中，水和空气的体积分数之和等于1，即：

式中：αw为计算域中每一个控制单元内水的体积分数；αa为计算域中每一个控制单元内空气的体积分数。

1.3 控制方程求解方法与边界条件

1.3.1 方程离散及求解方法

由于量水槽中的水流流动属于三维瞬态对流扩散问题，控制方程的离散采用有限体积法，对流项采用一阶迎风格式，扩散项采用中心差分格式。离散方程的求解采用2次压力修正的PISO （Pressure-Implicit with Splitting of Operators）算法。VOF方法中Y方向设置重力加速度值为-9.81 m∕s2。

1.3.2 边界条件

渠道进口分别设置气液2相进口边界，上部空气采用压力进口，压强大小与标准大气压相同，下部水流采用流量进口。巴歇尔槽进口流量分别设置为0.120 m³∕s、0.156 m³∕s、0.210 m³∕s、0.238 m³∕s，分别对应工况1、工况2、工况3、工况4 等四种工况。长喉道槽进口流量分别设置为0.057 m³∕s、0.220 m³∕s、0.393 m³∕s、0.487 m³∕s，也对应其工况1、工况2、工况3、工况4 等4 种工况。出口边界为自由出流，壁面设置采用壁面函数法。进口边界的湍动能和湍动能耗散率的计算为：

为验证数值模拟和边界条件的有效性，采用《灌溉渠道系统量水规范》（GB∕T 21303-2017）中给定的巴歇尔槽和长喉道槽流量公式进行模拟流量验证。规范中给定的巴歇尔槽和长喉道槽流量计算公式分别为：

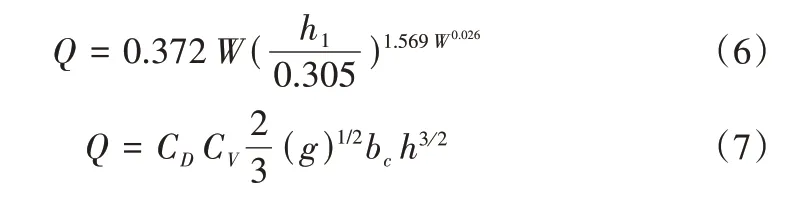
式中：Q为流量，m³∕s；h1为上游水尺水头，m；W为巴歇尔槽喉道宽度，m；CD为流量系数，CD=(H1/L-0.07)0.018；H1为上游渠段总水头，m；L为喉段长度，m；CV为行进流速系数；h为水位计实测水头，m；bc为长喉道槽喉道宽度，m。

2 结果与分析

2.1 模拟精度分析

表1 和表2 分别给出了巴歇尔槽和长喉道槽不同工况下模拟流量与计算流量的对比。从表1 和表2 可以看出，巴歇尔槽数值模拟流量与计算流量基本吻合，2者最大误差仅为2.16%，且随流量增加，模拟流量与计算流量的误差值逐渐减小；长喉道槽数值模拟流量与计算流量误差略大于巴歇尔槽，随流量增加，模拟误差值逐渐增大。但巴歇尔槽和长喉道槽数值模拟流量与计算流量的误差值均在10%以内，说明模拟结果可靠，可用于理论分析。

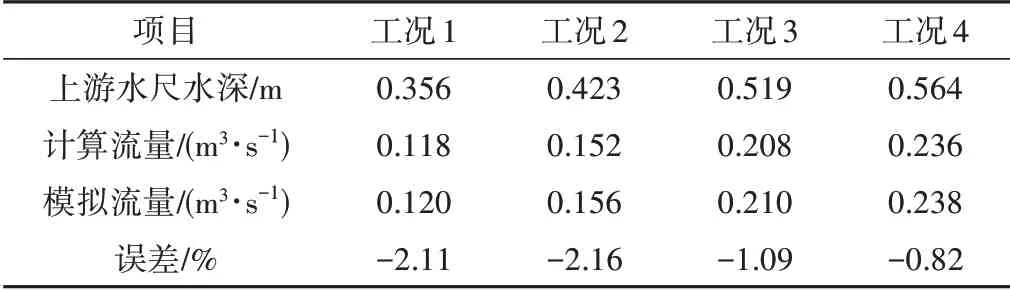
表1 巴歇尔槽模拟与实测流量对比Tab.1 Comparison between simulated and measured discharge of Parshall flume

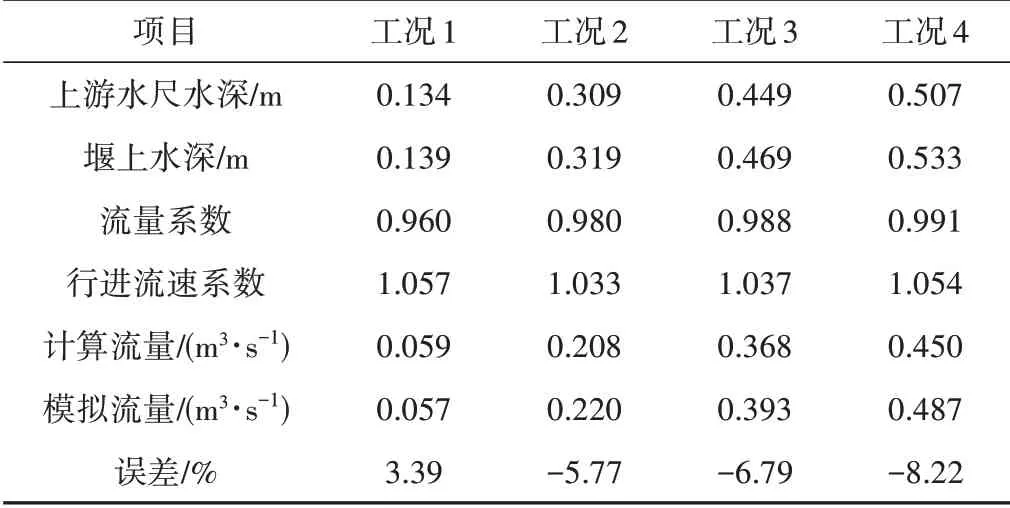
表2 长喉道槽模拟与实测流量对比Tab.2 Comparison between simulated and measured discharge of long-throated flume

2.2 水力特性分析

2.2.1 水面线分析

巴歇尔槽和长喉道槽设置上、下游渠道坡降均为1∕800，采用VOF 法处理水气交界面，确定水体积分数αw=0.5 的等值线为水面线。图3、图4 分别给出了巴歇尔槽和长喉道槽各工况下的水面线变化图。以巴歇尔槽喉道进口处为0-0断面，沿X方向-1.325 m 之前为进口段，-1.325～0 m 为收缩段，0～0.6 m 为喉道段，0.6～1.5 m 为扩散段，扩散段之后为出口段。

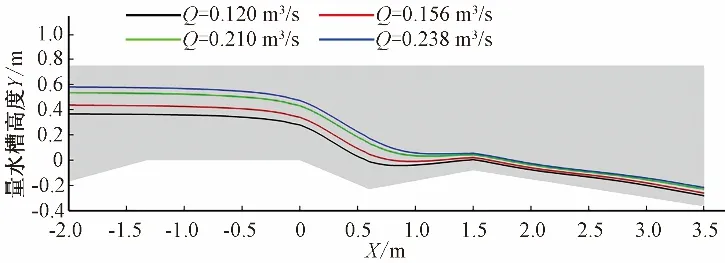
图3 巴歇尔槽不同流量下水面线Fig.3 Water surface profile of Parshall flume at different discharge

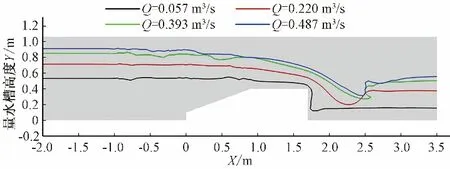
图4 长喉道槽不同流量下水面线Fig.4 Water surface profile of long-throated flume at different discharge

从图3可以看出，水流流经量水槽进口段、收缩段、喉道段时，由于流道逐渐缩窄，水流受平面上的束窄产生侧向和垂向的收缩，上游水位呈先壅高后又在收缩段逐渐降低的形态。水流由喉道段流向下游扩散段时，由于扩散段坡降增大和流道扩宽，水流流速增加，过流断面面积减小，槽内水位进一步降低。在经过巴歇尔槽时水流流态依次为缓流、临界流、急流3种流态，各流量下水面线过渡平缓，没有因流动边界变化而产生明显的漩涡。

从图4可以看出，由于受到量水槽侧向收缩和底部抬高影响，水流在经过长喉道槽进口段和收缩段时水面略有抬升，水面波动较大。在喉道段处，受槽底顶托作用影响，过流断面减小，流速增加，水面明显降落。由于扩散段量水槽底部为垂直跌坎，水面进一步迅速跌落，跌坎末端处水流从急流过渡到缓流，形成水跃，水面和坎脚处发生剧烈旋滚。

分别计算巴歇尔槽和长喉道槽不同流量下渠道段和喉道段临界水深如图5和图6所示。从图5、图6中可以看出，临界水深随着流量的增加而增加。2种量水槽前渠道段在最小流量Q=0.057 m³∕s 时临界水深为0.112 m，在最大流量Q=0.487 m³∕s时为0.366 m。由于受喉道段尺寸及断面形状变化影响，巴歇尔槽喉道段同流量下临界水深较上游渠道水深大，而长喉道槽喉道段同流量下临界水位较上游渠道段水深小。结合2种量水槽渠道水面线分析，各流量情况下，渠道段水深均大于临界水深，水流流态为缓流；而量水槽喉道处水深均小于临界水深，水流流态为急流。水流流态从缓流过渡到急流，导致水面线在槽内降低，发生明显的水跌现象。

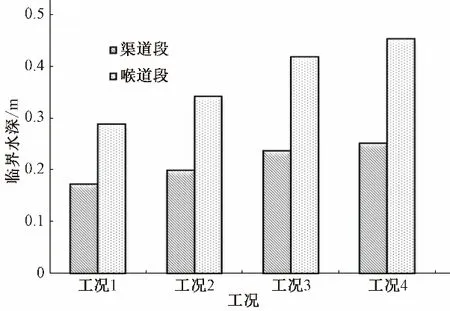
图5 各工况下巴歇尔槽渠道段和喉道段临界水深Fig.5 Critical depth of Parshall flume at channel and throat section for different discharge

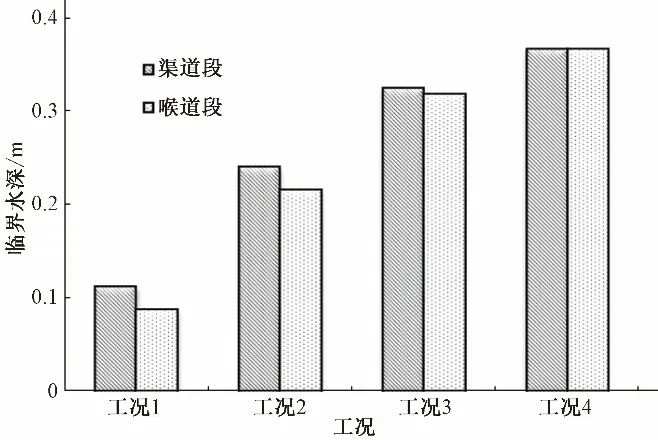
图6 各工况下长喉道槽渠道段和喉道段临界水深Fig.6 Critical depth of long-throated flume at channel and throat section for different discharge

2.2.2 流速及流线分析

图7 给出了中心纵断面（Z=0 切面）巴歇尔槽附近的流速分布及流线图。从图7 可以看出，不同流量下水流流过进口段、收缩段时受断面束窄作用影响，流速逐渐增加。流速变化和渠道边界会影响渠道内断面流线形状，流线在渠道段处相互平行，水流流态为均匀流；进口段和收缩段受边界条件影响，底部流线出现收缩，水流流态为渐变流；喉道段及扩散段流线曲率明显增加，水流流态为急变流；在出口段及下游渠道，流线又逐渐趋于平行，水流流态也从急变流过渡为均匀流。整个过程水流流态变化依次为均匀流——渐变流——急变流——均匀流。图8给出了中心轴线断面平均流速沿程变化，可以看出在喉道进口-0.5 m 以前断面处流速增加缓慢，在-0.5～0.5 m 处由于断面束窄和槽底坡度增加，流速显著增大；在喉道出口0.5 m 以后的断面，由于受扩散段负坡影响，流速呈现先减小后增大趋势，最后流速趋于稳定。在整个巴歇尔槽的进口段-收缩段-喉道段-扩散段-出口段内，流速呈现缓慢增大——显著增大——直线增大——略有减小——增大稳定的变化趋势。

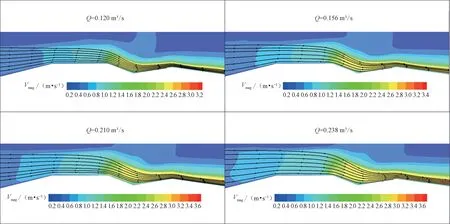
图7 巴歇尔槽中心纵断面（Z=0切面）量水槽附近的流速及流线分布Fig.7 Water velocity and streamlines of Parshall flume at Z=0 section

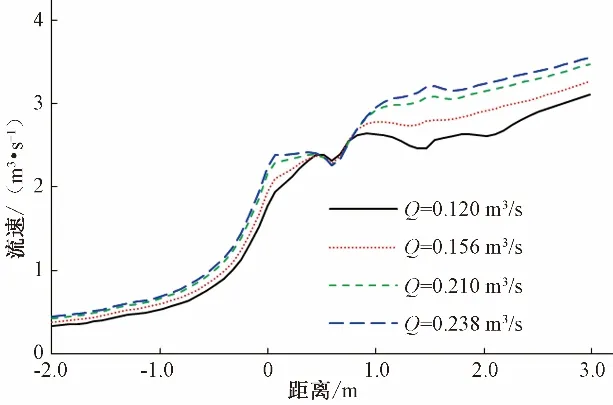
图8 巴歇尔槽中心轴线断面平均流速沿程变化Fig.8 Parshall flume mean velocity varies along the way at Z=0 section

图9给出不同流量情况下巴歇尔槽和长喉道槽喉道处的临界流速。可以看出量水槽进口处各流量水流流速均小于临界流速，水流流态为缓流；在量水槽出口处流速均大于临界流速，水流在经过量水槽时，流态从缓流转化为急流。图10 给出了中心纵断面（Z=0切面）长喉道槽附近的流速分布及流线图。从图10 可以看出，受长喉道槽底部抬升对水流的顶托作用，水深减小，流速逐渐增大，在喉道末端跌坎处，流速达到最大值，4 种工况下流速峰值分别为1.48 m∕s、2.48 m∕s、2.91 m∕s、3.00 m∕s。在扩散段处，由于下游水位抬升，水流在扩散段进口底部和水面处形成漩涡，消耗一部分水流能量，导致流速降低，扩散段之后流速增加并趋于稳定，水流在经过长喉道槽不同位置处流速变化为增大——减小——增大的过程。上游渠道内流线基本平行，水流流态为均匀流，长喉道槽及扩散段处，流线急剧收缩，曲率增大，水流流态为急变流；扩散段以后流线又趋于平行，流态又逐渐转化为均匀流，因此水流在长喉道槽内流态的变化过程为均匀流——急变流——均匀流。

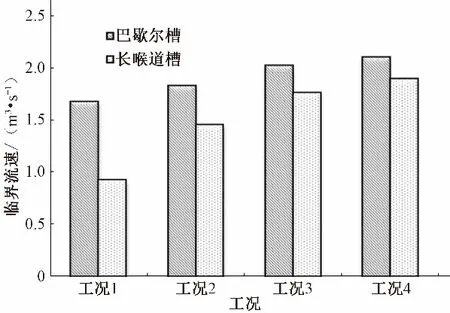
图9 巴歇尔槽和长喉道槽喉道处临界流速Fig.9 Parshall flume and long-throated flume critical velocity at throat section

2.2.3 水头损失变化

图11 给出了不同流量情况下巴歇尔槽与长喉道槽水头损失比。从图11 可以看出，在相同流量下长喉道槽水头损失明显大于巴歇尔槽，但巴歇尔槽水头损失随流量增大而增加，2者呈指数增长关系；而长喉道槽水头损失随流量增大而减少，2者呈负对数减小关系。

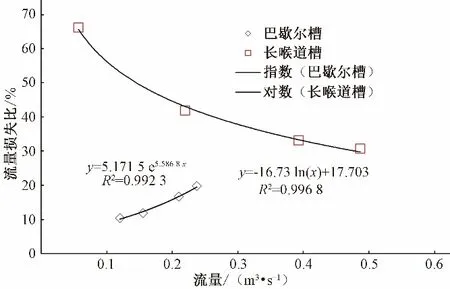
图11 各流量下巴歇尔槽和长喉道槽水头损失比Fig.11 Water head loss ratio of Parshall flume and long-throated flume at different discharge

水流流过量水槽时，水头损失包括沿程水头损失和局部水头损失。由于量水槽内水流为局部水力现象，加之水流流程较短，沿程水头损失可忽略不计，水头损失主要为局部水头损失。巴歇尔槽的局部水头损失由槽身侧向逐渐缩小后再逐渐扩大及槽底坡度起伏变化所引起。长喉道槽的局部水头损失由槽身侧向的逐渐缩小后再逐渐扩大及槽底突升突降所引起。巴歇尔槽喉道断面面积A喉与渠道断面面积A渠之比A喉∕A渠=0.211，长喉道槽喉道断面面积A喉与渠道断面面积A渠之比A喉∕A渠=0.520，在收缩角度小于15°时，各侧向收缩比下的局部水头损失系数均小于0.005；同样，在扩散角度小于15°时，不同扩散断面比下局部水头损失系数也均小于0.10。因此，将巴歇尔槽和长喉道槽在槽身侧向逐渐缩小和逐渐扩大的局部水头损失系数统一确定为0.105。巴歇尔槽4 种工况下槽身侧向断面变化产生的水头损失占总水头损失的比例依次为21.6%、21.3%、16.0%和14.3%，表明随流量增加，渠道侧向收缩和扩大产生的水头损失逐渐减小。长喉道槽4种工况下槽身侧向断面变化产生的水头损失占总水头损失的比例依次为2.2%、4.1%、6.1%和8.3%，表明随流量增加，渠道侧向收缩和扩大产生的水头损失逐渐增加。由于断面侧向变化引起的水头损失占总水头损失比重均小于25%，由此可知，水流经过量水槽时的水头损失主要为槽底起伏变化所引起的局部水头损失。巴歇尔槽底部变化比较平顺，而长喉道槽在喉道进口和出口处存在突升和突降，引起水流内部及表面发生旋滚，增加了水头损失，因此，同流量情况下，巴歇尔槽水头损失明显小于长喉道槽。

3 讨论

灌溉渠道系统量水的方式、设施和仪器已经有很多种，不同量水槽的水力特性不同，导致其测量精度、适用范围也不一样。因此，采用不同类型量水槽进行支渠以下小型渠道量水，从而满足精度高、使用方便、水头损失小、抗干扰性强、测量范围广的要求。

从量测精度来看，巴歇尔槽量水精度明显高于长喉道槽，且随着流量的增加精度越来越高。从不同流量情况下水面线变化可以看出，水流进入量水槽后由于喉道断面束窄，导致上游渠道水位抬升，流速减小，水面平稳，在喉道及扩散段，由于坡底起伏变化平缓，且发生距离较短，流速增加，水面平滑降落，流线稳定，从而保证了测量的精度。长喉道槽量水精度随着流量增加精度逐渐降低，水流在进入长喉道槽后，槽底抬升，上游水位壅高，由于长喉道槽前段进口为直角进口，水流内部发生旋滚，水面波动大，尤其是长喉道槽末端为垂直跌坎，在水流底部及表面均发生剧烈漩涡，水面波动剧烈，加之流量增加，下游水位抬升，自由出流程度降低，导致流量越大测量精度越差。

从水头损失来看，在流量小于0.4 m³∕s 时，巴歇尔槽水头损失小于长喉道槽，随着流量增加，水头损失呈指数增长。从上面分析可知，巴歇尔槽槽身断面变化对水头损失影响较小，其水头损失主要由于槽底宽度明显小于上游渠道，槽体对上游渠道产生壅水后，上下游水位差增加，流速显著加大而引起水头损失增加，且随着流量增加，壅水作用越明显，流速增加越剧烈，水头损失越大。长喉道槽喉道断面与上游渠道断面面积相比变化较小，槽体对水流的束窄及上游壅水作用不明显，局部水头损失主要由槽底直角进口与末端垂直跌坎引起的局部水头损失增大。在小流量情况下，局部水头损失系数在水头损失中起了决定性作用，随着流量增加，长喉道槽内水位升高，槽底变化所产生的局部水头损失系数作用逐渐减弱，因此水头损失随流量增加而逐渐减小。

在量水设施选型时，要求流量测量不确定度宜不超过±5%，且应选择水头损失小的量水设施，减小对渠道过流能力的影响。根据《灌溉渠道系统量水规范》（GB∕T21303—2017）的规定，巴歇尔槽在喉道宽度W=0.250 m时，流量量测范围为0.006～0.561 m³∕s，根据前面水头损失分析，随流量增加，喉道的壅水作用越发严重，水头损失也明显增加，在流量超过0.3 m³∕s 后，产生的水头损失占总能量的30%以上，从而严重影响渠道的过流能力。长喉道槽流量量测精度整体较巴歇尔槽偏低，且随着流量增加精度误差越来越大，但最大误差不超过10%；随着流量增加，水头损失越来越低，对渠道的过流能力影响减小。因此，综合考虑量水设施选型时，当量测流量较小时，选择巴歇尔槽作为量水设施，不但可以获得较高的量测精度，且水头损失小，不影响渠道的过流能力；当量测流量较大时，选择长喉道槽作为量水设施，产生的水头损失小，虽然量测精度略差，但仍控制在10%范围以内。