基于MGEX 站多系统GNSS 反演大气可降水量精度评估

郑志卿，张克非，李龙江，师嘉奇，张明浩

(中国矿业大学 环境与测绘学院,江苏 徐州 221000)

0 引言

水汽是地球大气中一种极为重要的温室气体，其在天气动力系统、测绘科学与技术以及水文学等诸多领域发挥着至关重要的作用.大气中的水汽受季节、地形和其他全球气候条件等因素的影响，具有时空分布不均匀、随时空变化较快等特性[1].水汽含量仅占大气总量的0.1%～3.0%，但却是大气中最活跃的部分，许多天气变化和自然灾害的发生都与大气中的水汽密切相关，在气候变化和天气预报中起着极其重要的作用[2-3].因此，研究水汽的时空特征有助于了解水汽的循环过程，为探究极端天气事件的产生及变化规律提供科学参考，同时水汽信息可用于暴雨、台风等强对流天气的监测和预报，对研究全球气候变化具有重要的科学和现实意义[4].

随着全球卫星导航系统(GNSS) 的不断成熟，GNSS 探测技术成为一种获取高精度水汽信息的新手段[5-9].该技术与传统大气水汽探测技术相比，如无线电探空仪、水汽辐射计、太阳光度计和卫星遥感等[10-11]，具有成本低、时空分辨率高、无仪器偏差和可实现全天候稳定观测等优点.近年来，地基GNSS技术已经被广泛应用于大气水汽的反演，文献[12]研究了Galileo 观测的数据实时反演可降水量(PWV)的精度，结果表明，利用精密单点定位(PPP)方法解算的方案得到的实时对流层天顶延迟(ZTD)与GPS 后处理得到的ZTD 吻合较好，伽利略反演的PWV 与利用欧洲中期气象预报中心(ECMWF)获得的PWV 具有良好的一致性.文献[13]对北斗三号卫星导航系统(BDS-3)的水汽探测性能进行了初步分析，结果表明，BDS-3 性能明显优于北斗二号卫星导航系统(BDS-2)，与GPS、ERA5 再分析数据具有很好的一致性.文献[14]利用56 个GNSS 测站反演的PWV，分析了厄尔尼诺现象对PWV 变化的影响，结果表明，海水温度每增加1 K，所有站点的PWV 就会增加11%.文献[15]通过GNSS 反演得到的PWV 建立了7 个预报因子的异常百分位阈值，建立的新模型对强降水正确探测率可达97.6%，平均提前时间为4.13 h.与现有模型相比，新模型的季节性虚警率降低了13.4%.

本文采用MGEX (Multi-GNSS Experiment)观测数据和武汉大学发布的WUM 最终精密星历，利用GAMIT 软件分别解算GPS、BDS、GLONASS 和Galileo 的观测数据，其中，BDS 同时包含BDS-2 和BDS-3 的观测数据.将4 个卫星系统估计的ZTD 与IGS 发布的对流层延迟产品对比，并将反演得到的PWV 分别与美国怀俄明州立大学的无线电探空(RS)数据及ECMWF 的ERA5 再分析数据计算的PWV 进行对比，评估GPS、BDS、GLONASS 和Galileo的水汽探测精度和可靠性.

1 地基GNSS 水汽探测原理

GNSS 信号在穿过大气层时受大气折射影响产生延迟，这一延迟按产生来源可分为两个部分：一是由电离层折射引起的电离层延迟，该延迟可通过组合不同频率的观测值得到很好地消除；二是由中性大气折射引起的延迟，主要由对流层引起，故一般称为对流层延迟.

1.1 ZTD

对流层延迟信息是GNSS 气象学中的主要研究对象.在GNSS 数据处理中，为了避免秩亏问题，通常将沿信号斜路径的对流层延迟映射到天顶方向[16]，即ZTD.ZTD 包含两部分：第一部分是由大气流体静力作用引起的延迟，称为天顶对流层静力学延迟(ZHD)；另外一部分是由大气中的水汽引起的延迟，即天顶对流层湿延迟(ZWD).ZTD、ZHD 和ZWD 的数学关系表达为

1.2 ZHD 和ZWD 的计算

ZHD 可由Saastamonien 模型[17]、Hopfield 模型[18]、Black 模型[19]估算.本文使用精度较高的Saastamonien模型计算ZHD，数学模型可表示为

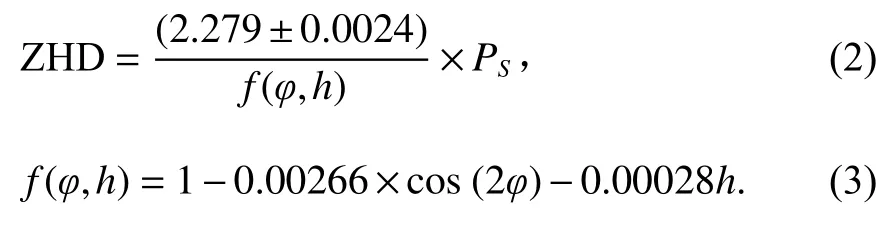
式中：PS为测站地面气压，单位为hPa；h为测站高程，单位为km；φ为测站地理纬度.

ZWD 主要是由大气中的水汽引起，难以对其进行准确建模.在GNSS 气象学中，通常从估算的ZTD 中减去ZHD 来获取ZWD，如式(4)所示：

1.3 GNSS-PWV 的计算

计算得到的ZWD 可由水汽转换系数转换为PWV，如式(5)所示：

式中，Π 为水汽转换系数，由式(6)计算.

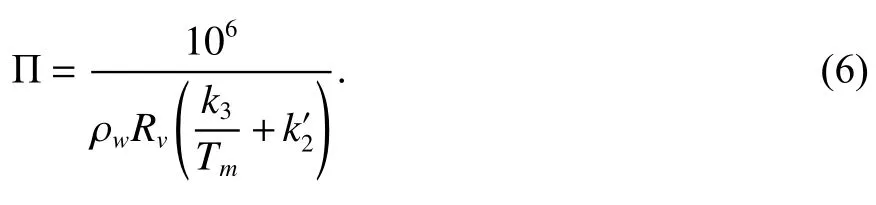
式中：Tm为加权平均温度，单位为K；ρw为液态水密度，取值为1 03kg/m3；Rv为水汽的气体常数，取值为461.518 J/(kg·K) ；、k3为大气折射率实验常数，分别为16.52 K/hPa、3.776×105K2/hPa.

1.4 探空、ERA5 数据计算PWV

由探空、ERA5 数据计算PWV 公式为

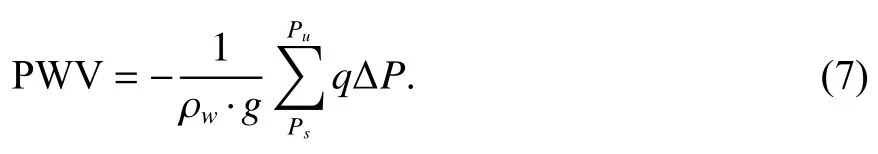
式中：g为重力加速度，近似取值为9.806 665 m/s2；q为比湿，单位为g/kg；ΔP为相邻两高度层之间的气压差；Ps、Pu分别为探空、ERA5 资料中记录的最低层与最高层的气压.

2 实验数据处理及分析

2.1 数据来源

为研究不同的卫星导航系统，国际GNSS 服务(IGS)建立了多模GNSS 实验跟踪网MGEX 用来跟踪、收集和分析来自GPS、BDS、Galileo以及GLONASS等多个卫星系统信号.

本文选取MGEX 中BRST、BRUX、CUSV、GRAC、IISC、JFNG、KIT3、OBE4、POL2、POTS、TASH、ULAB、URUM、WTZZ 及WUH2 共15 个站点的观测数据(下载地址：ftp://igs.gnsswhu.cn/pub/gps/data/daily)，时间范围为2021 年年积日第274—334 天，共61 天，其测站位置分布如图1 所示.

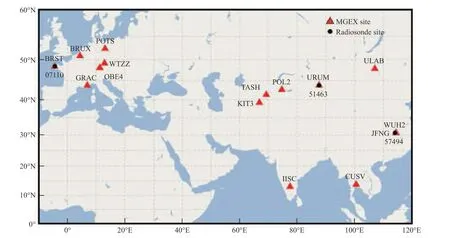
图1 MGEX 测站与探空站分布图

2.2 GNSS 数据解算策略

本文使用GNSS 高精度数据处理软件GAMIT，版本为10.75，采用双频无电离层组合方式，解算选取的15 个MGEX 站点的观测数据.对流层参数估计采用Saastamoninen 模型提供ZTD 先验值，并采用VMF1 映射函数模型.卫星星历采用武汉大学IGS 数据中心发布的时间分辨率为15 min 的WUM 最终精密星历文件(下载地址：ftp://igs.gnsswhu.cn/ pub/gnss/products/mgex/).GAMIT 软件解算时采用的解算策略具体参数设置如表1 所示.

表1 数据解算参数设置

2.3 探空数据获取

RS 法是目前公认较为可靠的PWV 测量方法之一，通过探空气球携带无线电探空仪的方式采集气球上升路径各个高度的温度、气压和比湿等实测数据[20].无线电探空仪计算的PWV 精度在毫米级，时间分辨率为12 h，可作为验证GPS、BDS、Galileo 和GLONASS探测水汽精度的外部基准.本研究使用美国怀俄明州立大学网站(http://weather.uwyo.edu/upperair/bufrraob.shtml)提供的编号为07110、51463 及57494 共3 个测站2021 年10 月至11 月的RS 站数据.

2.4 ERA5 气象再分析数据

气象再分析资料采用ECMWF 发布的第五代数据产品(1959 至今基于气压分层的ERA5)逐小时数据(下载地址：https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-press-ure-levels).ERA5 是ECMWF 使用最新的预测模型和数据同化系统对多源气象信息经重新分析得到的描述大气、陆地和海洋的全球气象数据集.与上一代ERA-Interim 产品相比，ERA5 具有更高的时间分辨率，时间分辨率最高可达1 h，其数据同化模型也有所改进.ERA5 数据详细描述如表2 所示.

表2 1959 至今基于气压分层ERA5 逐小时数据描述

3 ZTD 精度分析

3.1 截止高度角对ZTD 解算精度影响

在选取高度角时需要考虑多方面因素，过高的截止高度角会导致共视卫星数量减少，也会导致接收机与多颗卫星的高度角十分相似使得空间几何构型不稳定，影响解算精度.相反，截止高度角过小，信号在传播的过程中将更容易受到多路径效应的影响，对流层折射误差也会增大[21].过高或过低的截止高度角都会在不同程度上影响ZTD 的解算精度，选取合适的截止高度角对获取高精度的ZTD 至关重要.

为分析截止高度角对ZTD 解算精度的影响，利用2021 年年积日第305—334 天，共30 天的MGEX网中CUSV、IISC、JFNG、KIT3、POL2、TASH、ULAB、URUM、WUH2 共9 个测站GPS 的观测数据，将截止高度角分别设置为0°、5°、10°、15°、20°和25°.将IGS 分析中心提供的时间分辨率为5 min、精度为4 mm 的ZTD 产品作为参考值，对比不同截止高度角解算ZTD 的精度，IGS 中心发布的ZTD 记为ZPD.图2 为不同截止高度角解算得到的ZTD 与IGS 发布的ZTD 差值散点图，图2 显示截止高度角设置为20°和25° 时，IISC、JFNG、POL2、TASH、ULAB和URUM 6 个测站解算得到的ZTD 与IGS 发布的ZTD 差值离散度较大.

图2 不同截止高度角解算的GPS-ZTD 与IGS 发布ZTD 差值散点图

由表3 可知，截止高度角设置为5°时，利用GPS 观测数据解算出9 个测站ZTD 的bias 和RMS的平均值最小分别为0.21 mm 和5.72 mm，因此在后续分别解算GPS、BDS、Galileo 和GLONASS 观测数据时，均将截止高度角设置为5°.

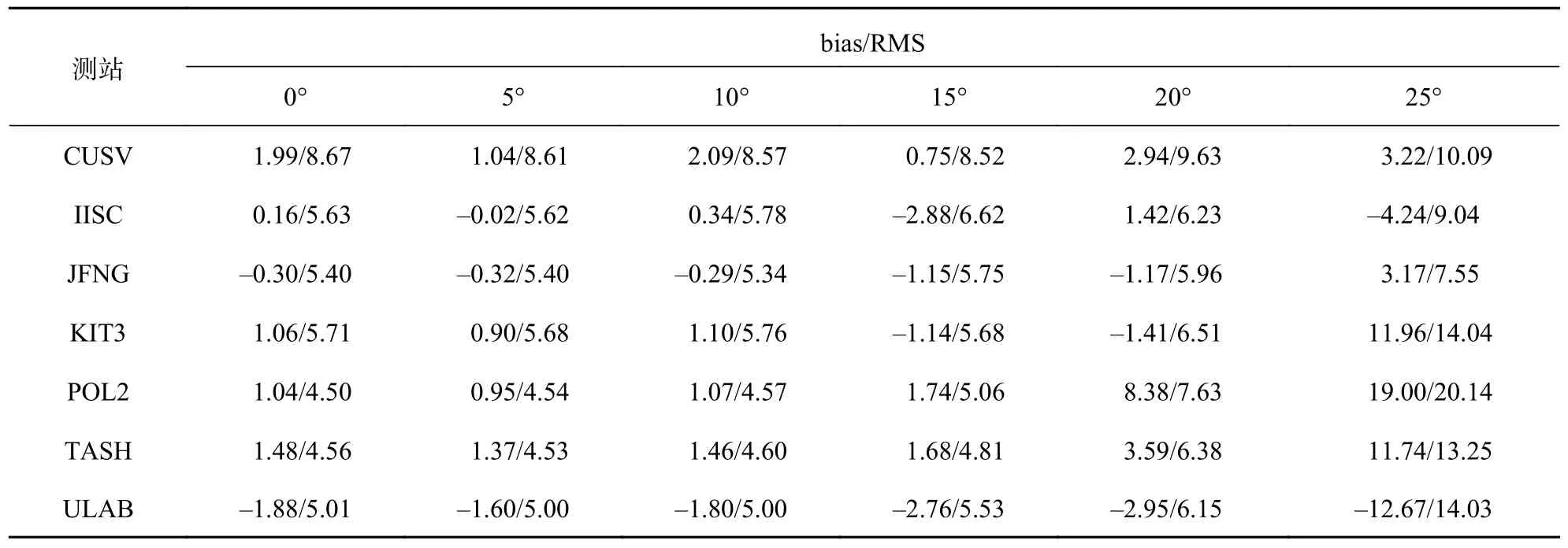
表3 不同截止高度角解算的GPS-ZTD 的bias 和RMS mm

表3（续）

3.2 ZTD 精度对比分析

图3 给出了BRST、BRUX、GRAC、POL2、POTS及TASH 6 个测站2021 年10 月1 日至11 月30 日ZTD 变化时序图.由图3 可知，GPS、BDS、Galileo和GLONASS 4 个卫星系统在BRUX、GRAC 及POTS 3 个测站估计的ZTD 与IGS 发布的ZTD 参考值符合均较好，且变化趋势基本一致，无明显系统bias.BDS 与GLONASS 在POL2 和TASH 测站估计的ZTD 与IGS 发布的ZTD 的一致性稍差.

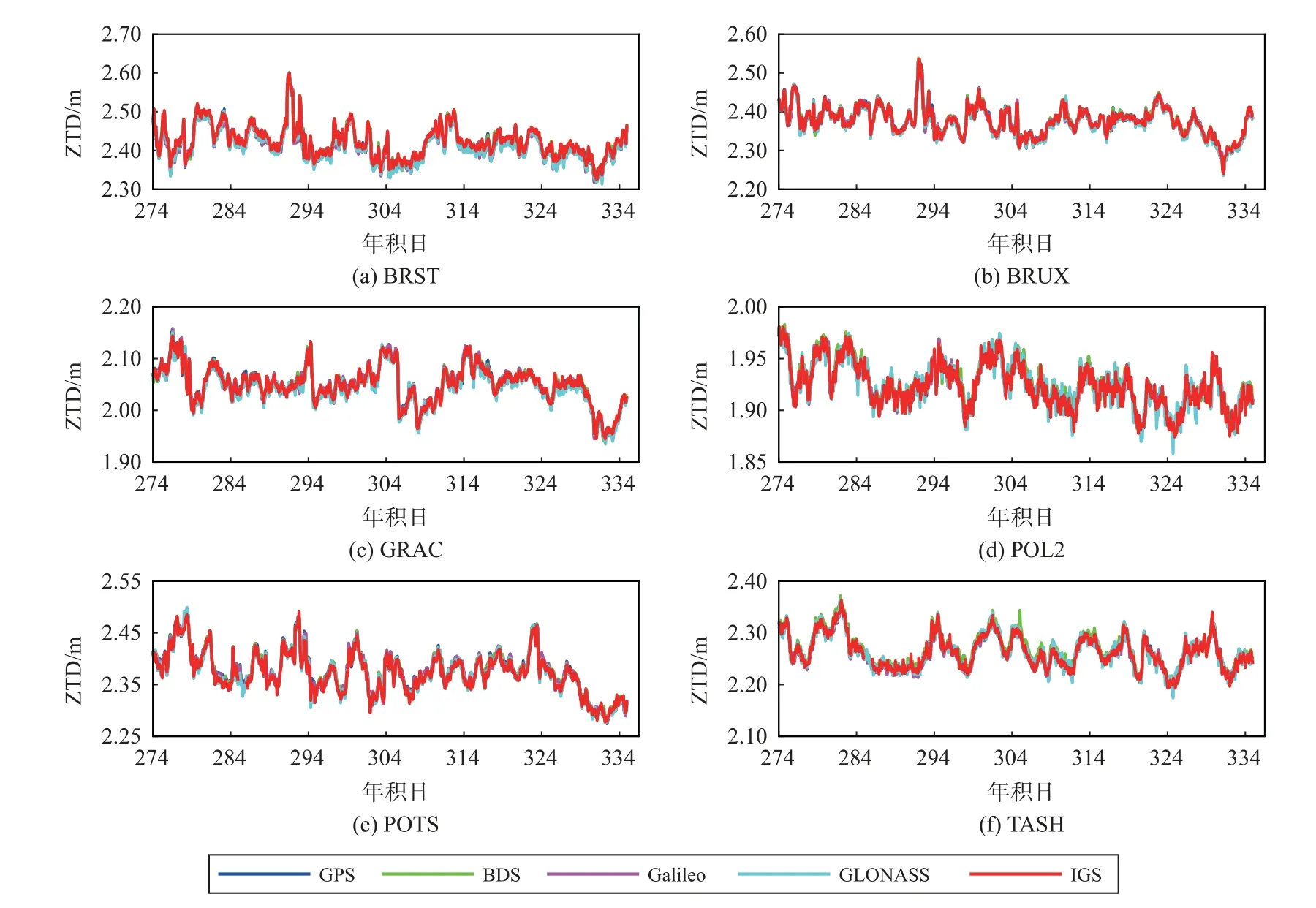
图3 ZTD 时间序列

图4 为4 个卫星系统在BRUX 和GRAC 测站估计的ZTD 与IGS 发布的ZTD 的线性相关性，GPS、BDS、Galileo 和GLONASS 估计的ZTD 分别记为GPS-ZTD、BDS-ZTD、Galileo-ZTD 和GLONASSZTD，IGS 发布的ZTD 记为IGS-ZTD.GPS-ZTD 与IGS-ZTD 符合最好，相关系数分别为0.990 和0.988，BDS-ZTD、Galileo-ZTD 和GLONASS-ZTD 与IGSZTD 相关性次之，相关系数分别为0.989 和0.986、0.987 和0.984、0.988 和0.979.

图4 GPS、BDS、Galileo 和GLONASS 解算ZTD 与IGS 发布的ZTD 相关性分析

图5 和图6 分别给出了GPS、BDS、Galileo 和GLONASS 在15 个测站处估计ZTD 的bias 和RMS，GPS-ZTD、BDS-ZTD、Galileo-ZTD 和GLONASSZTD 的bias 平均值分别为0.74 mm、1.06 mm、-0.15 mm 和-1.23 mm；RMS 平均值分别为5.81 mm、7.72 mm、6.85 mm 和8.66 mm.可以看出，在BRUX、GRAC、JFNG、OBE4、POL2、POTS、TASH、ULAB、URUM 和WTZZ 测站上，GPS、BDS、Galileo 和GLONASS 估计ZTD 的bias 的绝对值均小于3 mm，RMS 均小于10 mm.4 个卫星系统在BRST 和CUSV测站估计ZTD 的bias 和RMS 与其他测站相比其值较大，主要原因可能为BRST 和CUSV 测站邻近海域，导致ZTD 解算误差增大.

图5 各测站GPS、BDS、Galileo 和GLONASS 解算ZTD 的bias

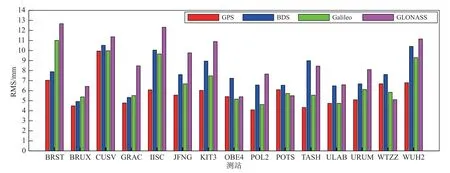
图6 各测站GPS、BDS、Galileo 和GLONASS 解算ZTD 的RMS

图7 为GPS、BDS、Galileo 和GLONASS 估计ZTD 的bias 和RMS 箱线图，对于单一箱线，从上到下各条水平横线依次表示上边缘、上四分位数、中位数、下四分位数和下边缘，箱线外部的符号为异常值.GPS-ZTD、BDS-ZTD、Galileo-ZTD 和GLONASSZTD 的bias 的中位数分别为0.48 mm、1.15 mm、-0.69 mm、-0.87 mm；RMS 的中位数分别为5.56 mm、7.60 mm、5.84 mm、8.45 mm.由图7 可知，GPS 估计ZTD 的精度最高，其次是Galileo，BDS 估计ZTD 的精度低于GPS 和Galileo，但精度高于GLONASS.

图7 GPS、BDS、Galileo 和GLONASS 解算ZTD 的bias 和RMS

4 PWV 精度对比分析

4.1 GNSS 反演PWV 与探空数据精度对比

将探空数据计算得到的PWV 作为参考值，记为RS-PWV，GPS、BDS、Galileo 和GLONASS 反演得到的PWV 分别记为GPS-PWV、BDS-PWV、Galileo-PWV 和GLONASS-PWV.图8 给出了4 个卫星系统在BRST、JFNG、URUM 及WUH2 测站反演PWV的bias 与RMS.GPS-PWV、BDS-PWV、Galileo-PWV和GLONASS-PWV 的bias 平均值分别为0.36 mm、0.19 mm、0.05 mm、0.26 mm；RMS 平均值分别为2.25 mm、2.46 mm、2.52 mm、2.84 mm.4 个卫星系统反演PWV 的bias 的绝对值均小于2 mm，RMS 平均值均小于3 mm.探空站点与GNSS 站点水平距离小于30 km 时，可认为探空站与GNSS 站点共址.由于BRST、URUM 站与各自邻近探空站点水平距离均小于30 km，反演的PWV 精度较高.4 个卫星系统在JFNG、WUH2 测站反演的PWV 精度低于BRST 和URUM 测站，主要原因为JFNG 与WUH2 测站与邻近57494 探空站点的水平距离大于30 km，导致反演得到的PWV 与RS-PWV 存在一定的系统bias.

图8 4 个卫星系统在测站BRST、JFNG、URUM 和WUH2 反演PWV 的bias 与RMS

4.2 GNSS 反演PWV 与ERA5 数据精度对比

RS 法探测水汽的精度虽然很高，但其时空分辨率较低，将ERA5 数据计算得到的PWV 作为参考值，记为ERA5-PWV，用于评估实验中的所有MGEX站点解算的PWV 精度.图9 给出了BRST、BRUX、GRAC、POL2、POTS 及TASH 6个测站2021 年10 月1 日至11 月30 日PWV 变化时序图，由图9 可知，GPS-PWV、BDS-PWV、Galileo-PWV 和GLONASSPWV 与ERA5-PWV 在BRST、BRUX 和POTS 测站一致性均较好，而在GRAC、POL2 和TASH 测站稍差.4 个卫星系统在6 个测站反演得到的PWV 的变化趋势与图3 中6 个测站ZTD 变化趋势几乎一致，表明PWV 与ZTD 具有很强的相关性.BRST、BRUX、GRAC 及POTS 4 个测站上空的PWV 含量与POL2、TASH 两个测站相比其值较大，主要原因可能为BRST、BRUX、GRAC 及POTS 4 个测站邻近海域，测站上空的水汽含量多于分布在内陆地区的POL2、TASH 两个测站.

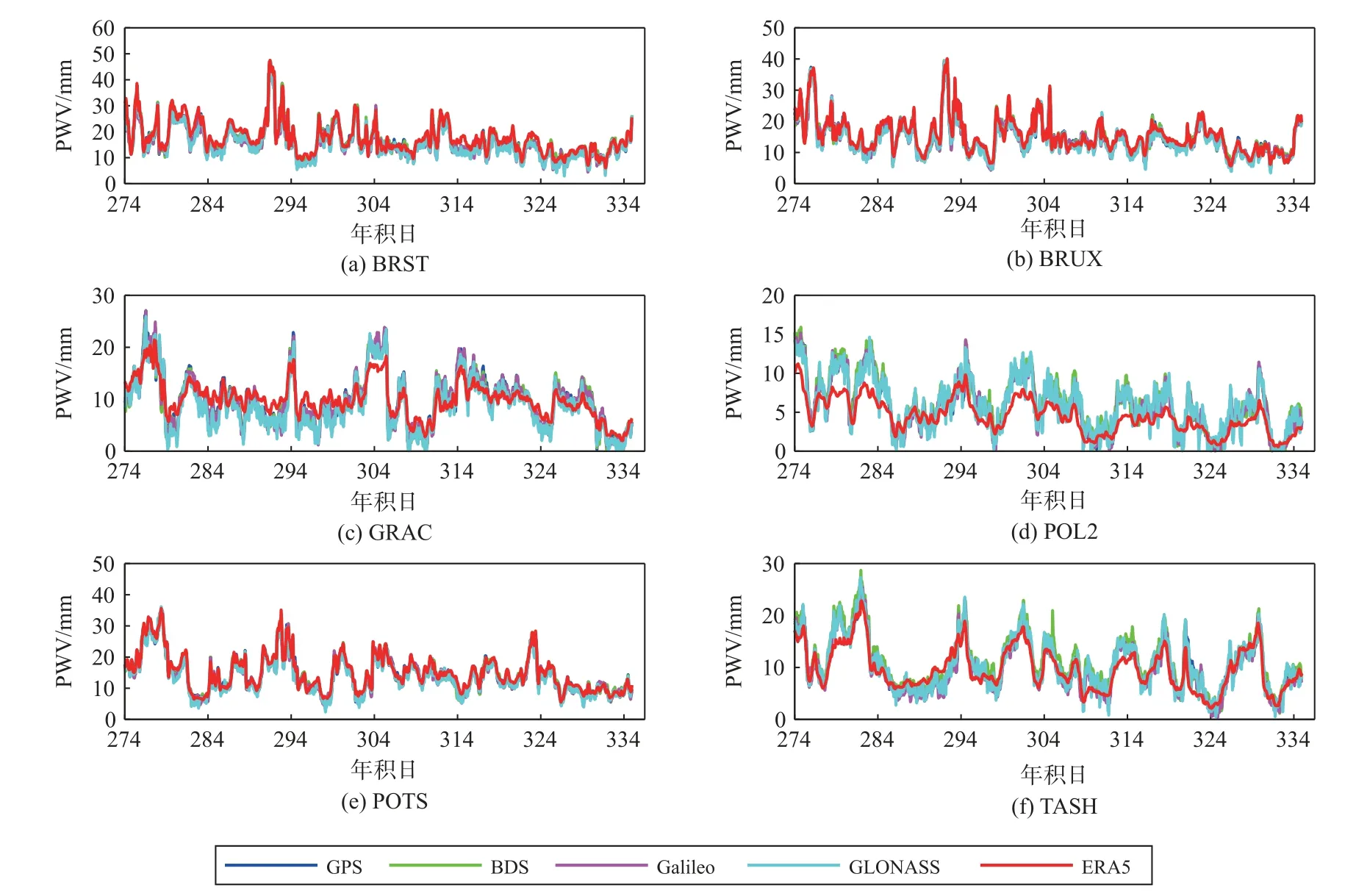
图9 PWV 时间序列

图10 为4 个卫星系统在BRUX 和GRAC 测站反演得到的PWV 与ERA5 数据计算得到的PWV 的线性相关性，在BRUX 测站，BDS-PWV 与ERA5-PWV 相关性最强，相关系数为0.962，GPS-PWV、Galileo-PWV、GLONASS-PWV 与ERA5-PWV 的相关系数分别为0.961、0.959 和0.958；在GRAC 测站，GPS-PWV 与ERA5-PWV 相关性最强，相关系数为0.905，BDS-PWV、Galileo-PWV、GLONASS-PWV 与ERA5-PWV 的相关系数分别为0.898、0.893 和0.886.

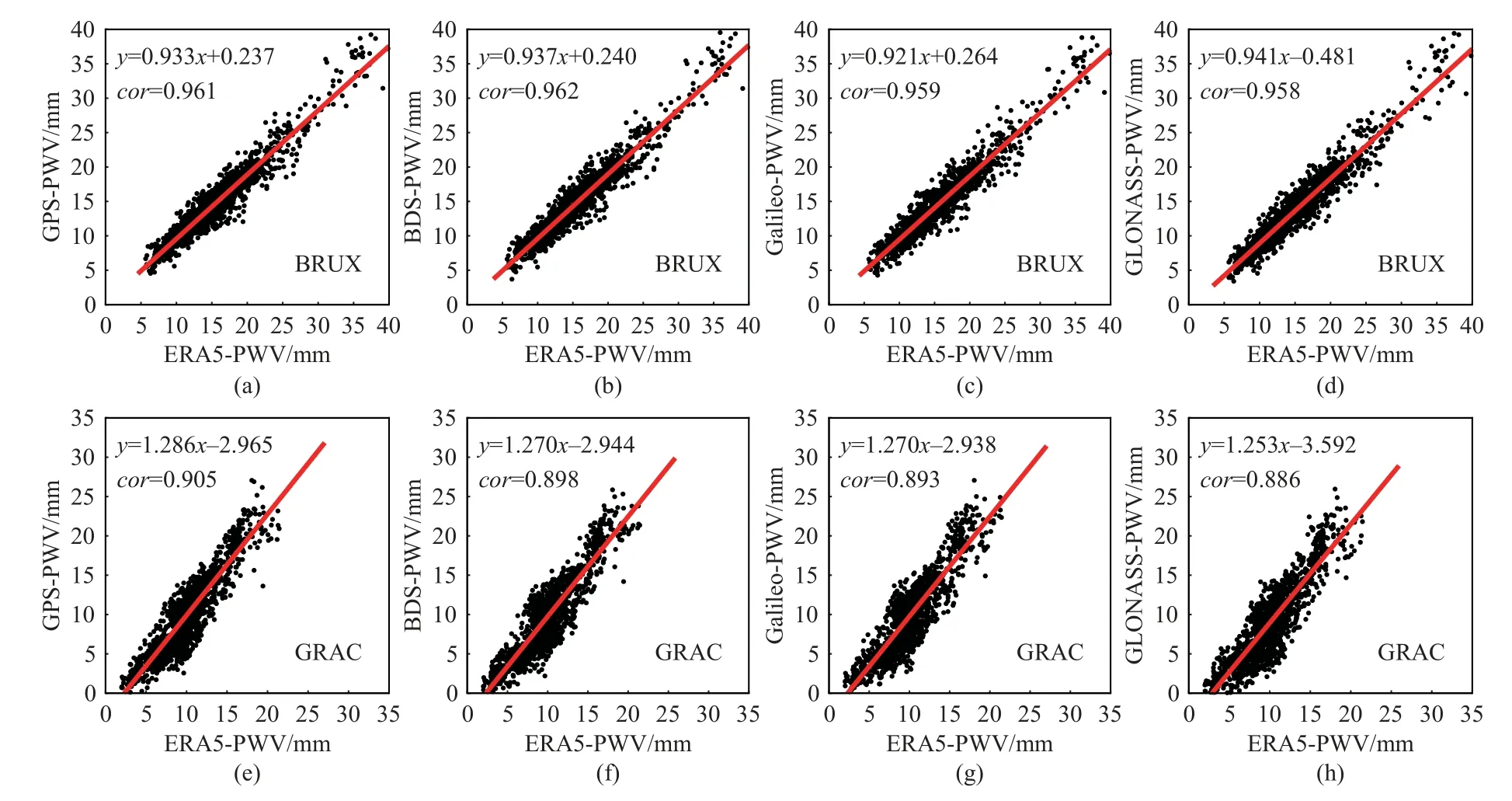
图10 GPS、BDS、Galileo 和GLONASS 反演PWV 与ERA5-PWV 相关性分析

图11 和图12 分别给出了以ERA5-PWV 作为参考值时，4 个卫星系统在15 个测站反演PWV 的bias和 RMS.GPS-PWV、BDS-PWV、Galileo-PWV 和GLONASS-PWV 的bias 平均值分别为0.33 mm、0.39 mm、0.22 mm、0.12 mm；RMS 平均值分别为1.63 mm、1.86 mm、1.76 mm、1.99 mm.4 个卫星系统反演PWV 的bias 的绝对值均小于2.06 mm，RMS 平均值均小于2 mm.由图可知，GPS-PWV、BDSPWV、Galileo-PWV 和GLONASS-PWV 的bias 的绝对值在大多数测站均小于1.5 mm，RMS 均小于2.5 mm.由 于GPS、BDS、Galileo 和GLONASS 在BRST 和CUSV 2 个测站估计ZTD 的bias 和RMS较大，因此反演得到的PWV 的bias 和RMS 也较大.

图11 各测站GPS、BDS、Galileo 和GLONASS 反演PWV 的bias

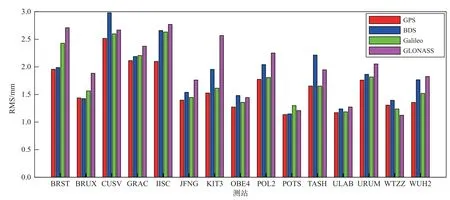
图12 各测站GPS、BDS、Galileo 和GLONASS 反演PWV 的RMS

图13 是GPS、BDS、Galileo 和GLONASS 4 个卫星系统反演大气可降水量PWV 的bias 和RMS 箱线图，GPS-PWV、BDS-PWV、Galileo-PWV 和GLONASSPWV 的bias 的中位数分别为0.51 mm、0.55 mm、0.29 mm、0.52 mm；RMS 的中位数分别为1.52 mm、1.87 mm、1.61 mm、1.95 mm.由图13 可知，GPS 反演PWV 的精度最高，其次是Galileo，BDS 反演PWV低于GPS 和Galileo，但精度高于GLONASS.

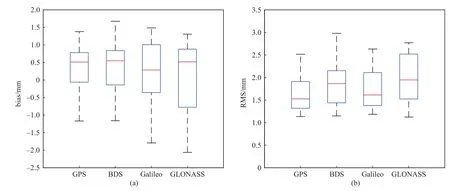
图13 GPS、BDS、Galileo 和GLONASS 解算PWV 的bias 和RMS

5 结束语

本文选取15 个MGEX 测站2021 年年积日274—334 天共61 天的观测数据，分析了GPS、BDS、Galileo和GLONASS 估计ZTD 与反演PWV 的精度，结果表明：

1) 在设置截止高度角为0°、5°、10°、15°、20°和25°的6 种实验方案中，截止高度角设置为5°时，可得到最优的ZTD 估计值.

2) 将IGS 发布的ZTD 作为参考值时，GPS-ZTD、BDS-ZTD、Galileo-ZTD 和GLONASS-ZTD 的bias 平均值分别为0.74 mm、1.06 mm、-0.15 mm 和-1.23 mm；RMS 平均值分别为5.81 mm、7.72 mm、6.85 mm 和8.66 mm.GPS估计ZTD 的精度最高，BDS 估计ZTD 的精度低于GPS 和Galileo，高于GLONASS.

3) 将探空数据计算得到的PWV 作为参考值时，GPS-PWV、BDS-PWV、Galileo-PWV 和GLONASSPWV 的bias 平均值分别为0.36 mm、0.19 mm、0.05 mm、0.26 mm；RMS 平均值分别为2.25 mm、2.46 mm、2.52 mm、2.84mm.4 个卫星系统反演PWV的bias 的绝对值均小于2 mm，RMS 平均值均小于3 mm.将ERA5 数据计算得到的PWV 作为参考值时，GPS-PWV、BDS-PWV、Galileo-PWV和GLONASSPWV 的bias 平均值分别为0.33 mm、0.39 mm、0.22 mm、0.12 mm；RMS 平均值分别为1.63 mm、1.86 mm、1.76 mm、1.99 mm.4 个卫星系统反演PWV的bias 的绝对值均小于2.06 mm，RMS 平均值均小于2 mm.GPS 反演PWV 的精度最高，BDS 反演PWV 的精度低于GPS 和Galileo，高于GLONASS，均满足气象学应用需求.