一种拟合三维复杂螺旋刀具轨迹NURBS插值逼近方法

2022-11-05邓华波王玮琪梁务宇刘思远

沈阳建筑大学学报（自然科学版） 2022年5期

邓华波，王玮琪，梁务宇，刘思远

(沈阳建筑大学机械工程学院，辽宁沈阳 110168)

航空、航天、航海领域中所用的叶轮叶片的加工要求加工精度高、加工表面光顺等特点以实现设备行驶过程中的噪声减小[1-2]，但由于此类零件形状通过空气动力学等复杂公式计算得到，零件表面极为复杂，一旦其数控加工刀具路径规划不合理，将导致机床加工出的零件误差较大、表面不光滑。因此，很多学者在上位机进行数控加工轨迹的规划及刀具速度、刀轴矢量的优化[3-4]，然后后处理生成G代码或采用NURBS插补器加工，进而解决加工时的加工精度和表面光顺问题。也有学者通过对曲面拟合的方式求解复杂曲面数控加工的刀具路径规划问题，在曲面造型中拟合精度要求较高[5-6]，精加工叶片时生成的刀具路径是的空间螺旋曲线，加工时无退刀、无抬刀、省时[7]。以往学者大多在平面上进行曲线拟合[8-10]，而空间复杂螺旋曲线投影至平面会产生变形导致拟合结果较差，从而影响刀具路径规划效果。故笔者在数控加工路径规划中直接对复杂空间螺旋曲线进行三维空间拟合。

空间曲线拟合方法中一般通过最小二乘法[11-13]选择部分数据点经过插值反求得到拟合曲线并计算拟合误差，若拟合精度没达到要求，则增加数据点的数量重新插值并计算拟合误差，直到达到拟合误差要求为止。很多学者采用遗传算法、粒子群算法等对曲线最小二乘法逼近拟合进行优化[14-15]，但在空间中，逼近算法容易陷入局部最优解，导致运算量庞大[16-17]。S.Tulsyan等[18]提出了一种拼接方法，将相邻的线性导轨段之间插值同步的五次B样条用来平滑刀轴矢量位置和方向。该方法中，公式参数的连续性对曲线的连续性有很大的影响，拼接后需要降阶，并且五次B样条的公式过于复杂，计算基函数时计算量大，且B样条在描述非抛物线时会产生一定的误差。SHEN Liyong等[19]给出了一种利用三次Bezier样条曲线在给定参数区间逼近的方法，由于Bezier样条灵活特性，改动一个控制点，全部控制点会发生变化，会导致在误差计算时的计算量大，效率低。NURBS技术是目前国际标准组织(ISO)规定的表示自由型曲线曲面的唯一国际标准。工程中一般使用C2连续的三次NURBS曲线进行拟合，拟合结果光顺、计算量小、计算快、精度高。但C2连续的三次样条曲线在光顺时使一些数据点程度不同的偏离原始位置，有时会出现超出规定的误差[20]。LIU Jiyuan[21]采用调整权因子的方式来改变局部曲线形状，但在空间复杂螺旋曲线插值拟合过程中误差较大点处调整的效果不明显，并且权因子的调整要通过计算拟合曲线与原始数据点的最短距离，计算量庞大，且权因子的调节规律性不强。全局插值法虽然使拟合后的曲线尽可能穿过原始数据点，但仍有部分拟合误差较大。由于全局逼近或其他方法拟合后的曲线穿过原始数据点的数量不如全局插值拟合方法多，但全局插值在部分点的拟合误差较大无法达到工况要求的拟合精度。由于NURBS曲线的局部可调性，笔者提出一种基于非均匀有理B样条拟合的空间螺旋刀具路径整体插值逼近方法，通过插入虚拟数据点，并计算插入数据点后的曲线扎人合误差，拟合后的曲线仅用一个公式对空间复杂螺旋轨迹进行表达，为优化刀具的进给速度或刀轴矢量提供数学表达式，拟合误差能达到精加工的要求、误差变化幅度明显减小情况下，计算量较小。

1 空间螺旋刀具路径的三次NURBS曲线拟合

1.1 NURBS曲线表示与节点计算

三维空间的NURBS曲线定义为对于给定的控制点di=[xiyizi]及其权因子ωi(i=0,1，…,n)，其带权控制点Di=[ωidiωi]=[ωixiωiyiωiziωi],定义一条四维的k次非有理B样条曲线P(u)，取它在第四坐标ω=1的超平面上的中心投影，能够得到三维空间的一条k次NURBS曲线p(u)。步骤如下：

(1)确定所给控制顶点di=[xiyizi]的带权控制点Di=[ωidiωi]=[ωixiωiyi

ωiziωi]。

(2)定义一条四维k次非有理B样条曲线。

(1)

(3)将其投影到ω=1超平面上并获得一条k次NURBS曲线p(u)。

(2)

其中，Ni,k(u)为由节点矢量。

U=[u0,u1,…,un+k,un+k+1],为按de Boor-Cox递推公式决定的k次规范B样条基函数。

当k=0时，

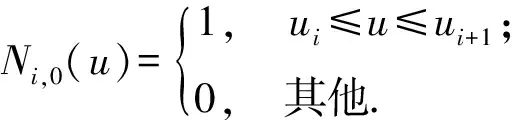
(3)

当k∈[1,+∞)时，

(4)

通过对型值点的参数化得到节点矢量。NURBS曲线一般采用弦长参数化法效果较好，其中福利参数化法下生成的插值曲线显现出最好的光顺性，拟合误差较小。其计算公式为

(5)

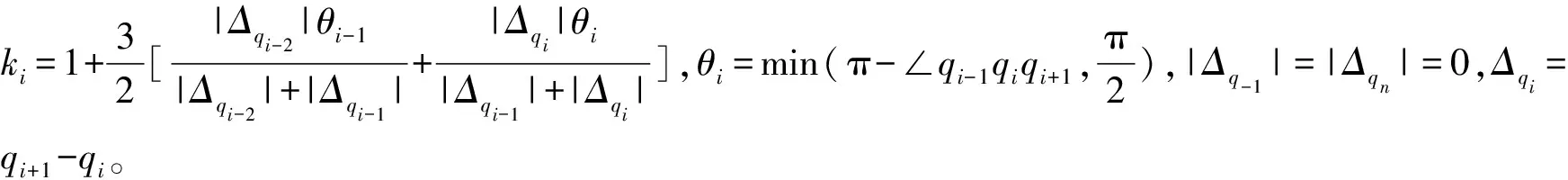
规范化使节点矢量在[0，1]内，进而得到(u0=…=uk=0,uk+1,…,un+k=…=un+2k=1)节点矢量。

1.2 边界条件定义

由于节点矢量中存在重复的节点[19]，会导致首(末)顶点和首(末)数据点重合，首末端点处的条件不足。因此，需要增加由边界条件确定的附加方程求出带权控制顶点Di，然后将带权控制顶点在ω=1的超平面上进行投影，得到待求控制顶点di。当ωi(i=0,1，…,n)都为1时，非均匀有理B样条曲线就转化为非均匀B样条曲线。因此只要定义非均匀B样条的边界条件亦可求出非均匀有理B样条曲线的边界条件方程。采用连续的C2三次NURBS曲线对空间螺旋曲线进行拟合，要求曲率均匀变化，首末端点采用抛物线条件，有二阶导且为实数。

首端点抛物条件：

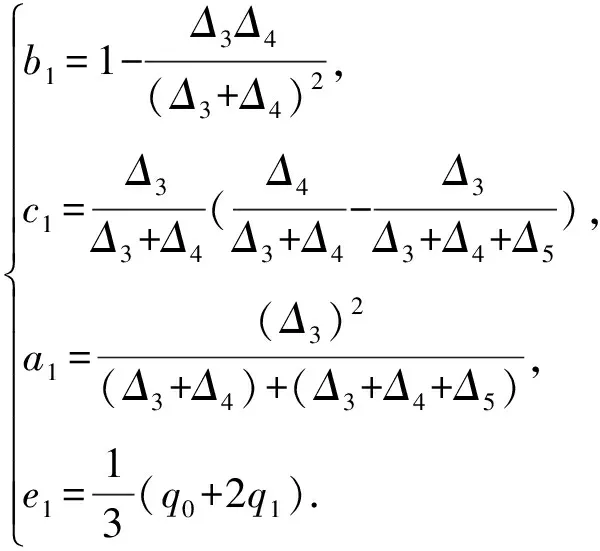
(6)

末端点抛物条件：

(7)

1.3 控制顶点求解

通过式(1)对3次非有理B样条曲线的定义，可知当ωi都为1时，NURBS曲线即为3次非均匀B样条曲线。

根据反算C2连续的三次B样条插值曲线的控制顶点矩阵方程：

(8)

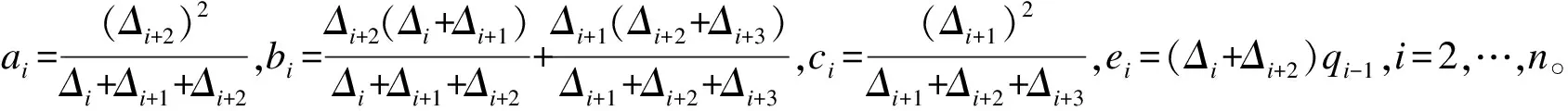
曲线首端点与第一个型值点重合，末端点与最后一个型值点重合q0=d0，qn=dn+2。矩阵方程(8)中首行的元素b1、c1、a1与e1表示首端点边界条件。末行的bn+1、cn+1、an+1与en+1表示末端点边界条件。

采用追赶法解方程(8)，求出全部控制顶点di，对于非均匀有理B样条，只需将方程(8)中的di改成带权的控制顶点Di=[ωidiωi]，再投影到ω=1超平面上，即用ωidi除以ωi就得到控制顶点di。

1.4 拟合误差计算

原数据点到空间曲线的最短距离为曲线拟合误差，通过设定允许误差界ε，若得到的拟合曲线最大误差在允许的误差界ε内，则可作为最终曲线使用。求解曲线的最大拟合误差，一般通过曲线p(u)到型值点qi的距离，取得qi到曲线点最短距离。豪斯多夫距离是曲线拟合偏差检查通常检查最大范数距离，其公式：

(9)

其中，qi为原始型值点；p(u)为拟合得到的曲线上的点。实际拟合过程中，型值点qi到拟合曲线p(u)的最短距离可通过二分法快速得到一个允许误差范围的近似解。

2 插值逼近拟合方法的求解

2.1 拟合方法的求解流程

笔者综合运用插值、逼近算法实现曲线拟合算式的求解，插值逼近拟合方法的算法流程如图1所示。通过导入数据点即原始数据点，选择曲线曲率变化较大处的特征点qm。确定特征的位置点qm和要插入的虚拟数据点的数量和位置。插入虚拟数据点后，对所有点进行NURBS全局插值，对u在区间[m+2-r,m+4+r]的曲线采用式(9)进行拟合误差计算，采用二分法计算。当计算得到的拟合误差大于指定误差时，停止对剩余曲线误差的计算，进入下一步增加虚拟数据点的插入数量。

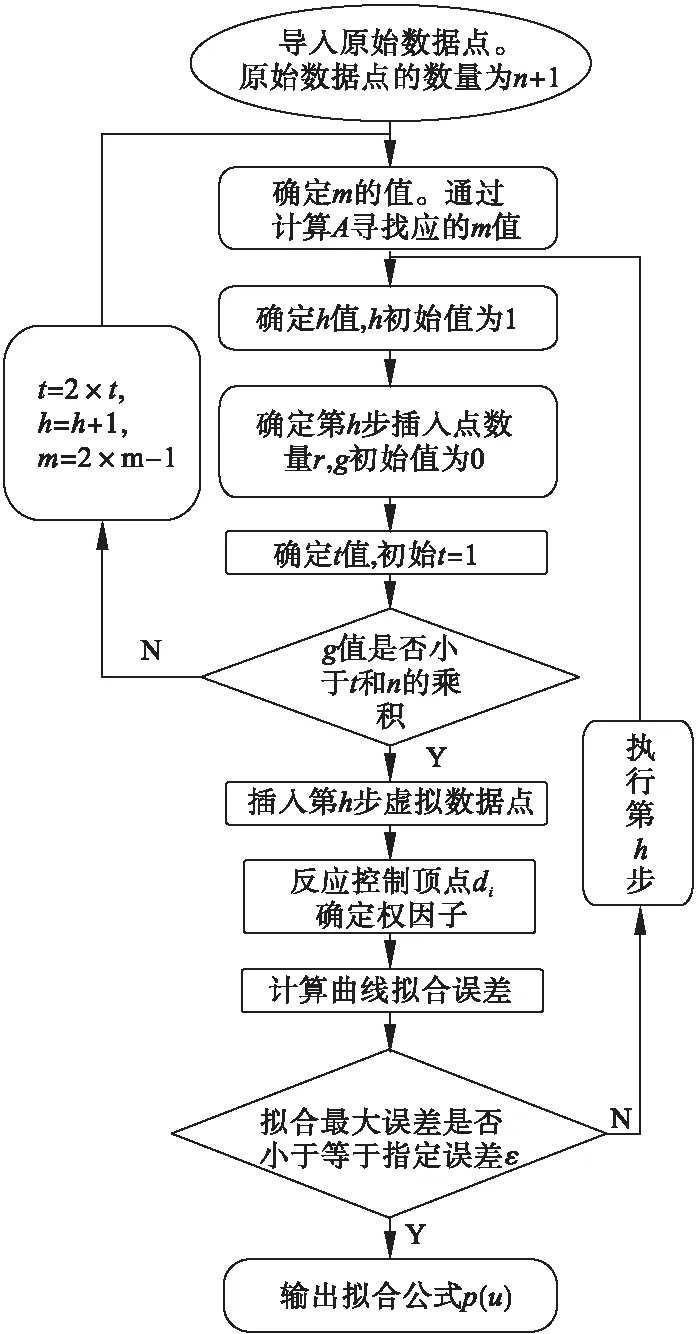
图1 插值逼近方法求解流程Fig.1 The flow of interpolation approximation

插入虚拟数据点后，再对所有点进行NURBS全局插值，对u在区间(其中r为特征点两侧各选取的原始型值点数量)，曲线采用式(8)进行拟合误差计算，采用二分法或牛顿迭代法计算。当计算得到的拟合误差大于指定误差时，停止对剩余曲线误差的计算，继续增加虚拟数据点的插入数量g。然后重复计算过程，直至计算得到的拟合误差全者小于指定误差为止。

2.2 寻找特征点

在复杂曲面刀具路径生成过程中，常采用导入原始型值点，同时考虑曲线的挠率和曲率。为避免计算时受空间维度限制，曲线可看成由连续原始数据点qi、qi-1、qi+1所在平面上的弧线组成，根据圆弧估算法求离散曲率κi的公式[16]：

(10)

其中,夹角∠qi-1qiqi+1的区间为[90°,180°]，|qi-1qi+1|为弧线的弦长。

Am+1=‖qi+1qi+3|-|qiqi+2‖×|∠qi+1qi+2qi+3-∠qiqi+1qi+2|.

(11)

图2 A与m值的关系图Fig.2 The relationship between A and m

2.3 虚拟数据点插入

将虚拟型值点添加在相邻两个原始型值点之间的直线上，在特征点qm两侧各选取原始型值点数为r。在特征点qm前后先各加0个虚拟型值点。通过计算分析当特征点两侧所选择的原始型值点的数量小于等于3时，插入虚拟型值点的位置在相邻两原始型值点线段上，距离前一点的5/8处拟合误差较小，如图3中qm-1与qm之间线段上距离qm点5/8处的点J。当添加虚拟型值点前后各添加点数大于3时，根据计算在相邻两原始型值点线段中点位置添加虚拟数据点，拟合后的最大误差相较其他位置最小。

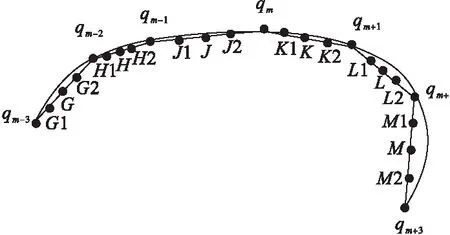
图3 虚拟数据点添加位置Fig.3 The add location for virtual data point

若拟合误差小于指定误差，则确定NURBS曲线公式符合工况要求。若大于指定误差，则将添加型值点的个数前后各增加1，在原始型值点qm前后先各插入1个虚拟型值点，图3中J点和K点。若大于指定误差，插入图3中的H、L点。本次添加的虚拟型值点位置在图3中的H、J、K、L点，拟合后计算与原始型值点的最短距离中的最大值与指定误差比较，若大于指定误差则继续增加型值点个数，即图3中的G、H、J、K、L、M。当添加虚拟型值点前后各添加点数大于3时，根据计算在相邻两点线段中点位置添加型值点，拟合后的最大误差相较其他位置最小。因此，当添加虚拟型值点前后各添加点数大于3时，添加型值点的位置变为相邻两点线段中点位置。通过不断添加虚拟型值点，并计算相应的拟合误差。以上为插入虚拟型值点总数g小于n时的情况。

当曲线最大拟合误差大于指定误差ε且插入虚拟型值点总数g等于n×t时，h值增加1，当本次拟合误差大于指定误差时，执行步数为h+1步，重复上述过程，并以此类推。

2.4 拟合误差计算

根据式(9)得到拟合误差计算公式:

(12)

其中，ε为指定误差。通过二分法或牛顿迭代法快速计算插入虚拟型值点部分的曲线u的范围为[m+2-r，m+4+r]上的拟合点与原始型值点之间的最短直线距离得到一个允许误差范围的近似解，m按从小到大的顺序取，只要有一个m所在区间的拟合误差值大于指定误差C2就停止拟合误差的计算，进入下一步。若区间上所有曲线最大拟合误差小于或等于指定误差ε，则得到所求NURBS曲线公式。

3 局部逼近拟合方法算法算例

3.1 插值逼近方法算例

算例采用如图4所示的叶片模型，其工件坐标系下刀具路径的刀位点为笔者算例的数据点。叶轮毛坯直径为100 mm，选用球头铣刀，采用叶片精加工驱动方法，切削模式选用螺旋铣削模式。行距参数采用等高残留法并设置0.2 mm的残留高度，设置加工时内外公差均为0.02 mm，通过UG软件实现刀具路径的初步规划如图4所示。

图4 刀具路径Fig.4 The tool path

将工件坐标系下的刀具路径导出，文件格式为CLS。刀具路径文件数据中，前三列为刀位点数据，分别对应工件坐标系X、Y、Z轴。算例生成的刀具路径共2 637个数据点。精加工叶轮叶片允许误差设为0.02 mm，拟合误差为加工误差的1/5时对叶轮叶片加工影响较小，故算例设定NURBS拟合最大误差为 4 μm。

导入数据点，通过式(11)计算乘积A值，m为刀具路径文件中的刀位点序列号。A与m关系如图5所示。计算乘积A的平均值，并找出大于乘积A平均值的对应点分别为第m个。

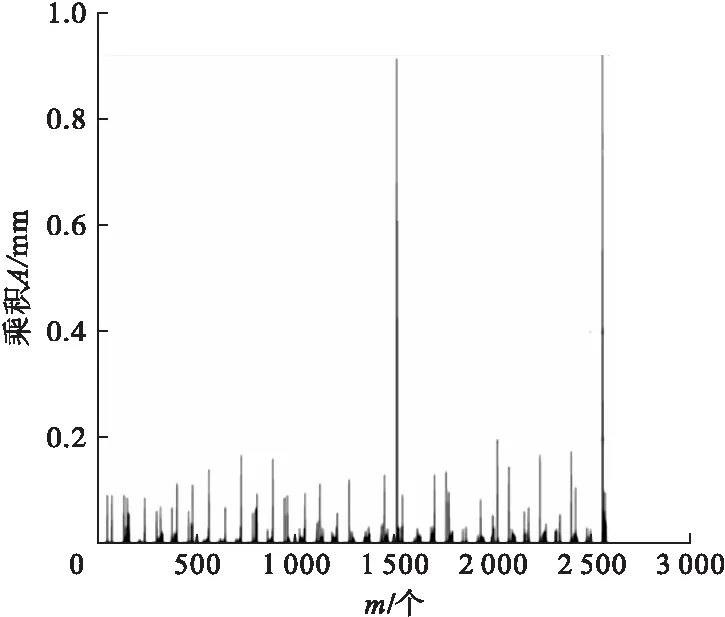
图5 算例中A与m值的关系图Fig.5 The relationship between A and m

超过A平均值所对应的m值有343个。按局部逼近拟合方法步骤在qm前后各插入0个虚拟型值点，此时为全局插值拟合，此时计算通过式(9)计算曲线拟合误差，可得到最大拟合误差为0.025 0 mm，拟合误差大于4 μm，则根据插值逼近法流程添加插入虚拟型值点的个数并根据式(11)计算相应曲线段的拟合误差。当r为3时得到刀具路径曲线拟合误差，如图6所示。

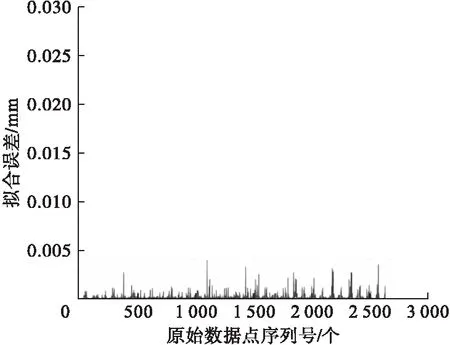
图6 插值逼近法拟合误差Fig.6 The fitting error of interpolation approximation

3.2 两种方法拟合误差参数对比

通过全局插值方法拟合曲线，并采用式(9)计算得到2 637个数据点拟合后误差，全局插值方法拟合误差如图7所示。

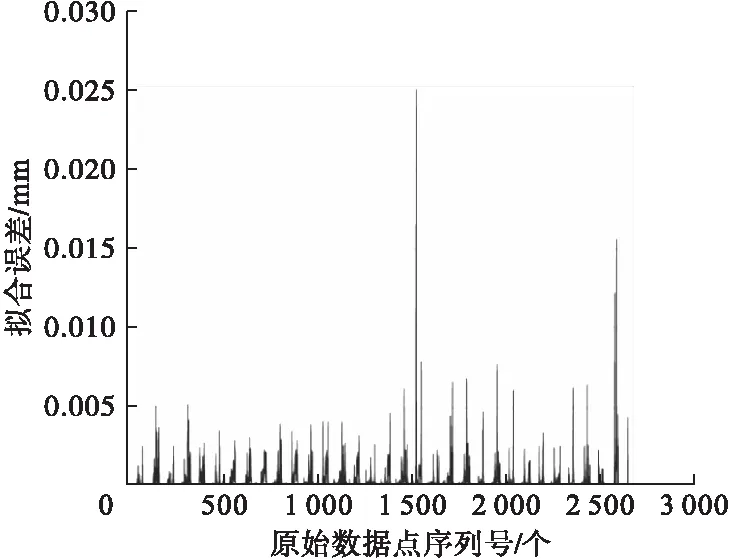
图7 全局插值拟合方法拟合误差Fig.7 The fitting error of global interpolation fitting method

将插值逼近的拟合误差结果如图6所示，对比两种拟合方法的最大误差、控制顶点以及方差(见表1)。

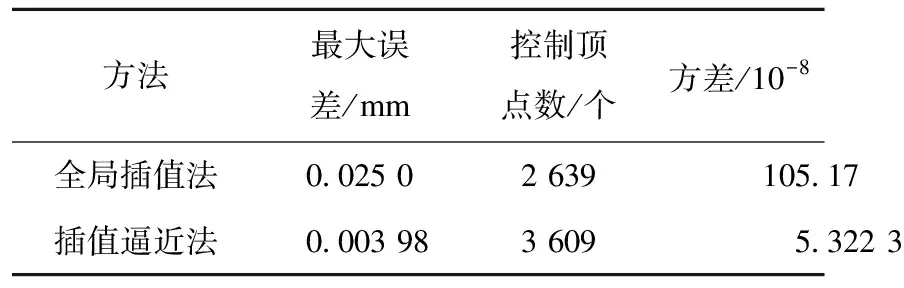
表1 两种方法拟合2 637个数据点后曲线参数对比Table 1 Comparison of curve parameters after fitting 2 637 data points by two methods

对两种方法拟合后的误差、控制顶点数以及方差进行比较，在提供数据点相同的情况下，笔者方法的最大误差和方差远小于全局插值方法。当要求最大拟合误差达到4 μm以下时，采用最小二乘法在拟合时需要重复计算整段曲线的拟合误差，而笔者方法仅需重复计算部分曲线段的拟合误差，且需要计算拟合误差的曲线段长度小于整体曲线段的36.7%，并且拟合得到的曲线穿过大部分的型值点，在C2参数连续的情况下，能够更准确的表达刀具路径的特点。