基于DIC的预应力节段拼装桥墩变形成分分析

2022-11-05王东升李俭涛付建宇

沈阳建筑大学学报（自然科学版） 2022年5期

王东升，陈贺，李俭涛，付建宇，葛笑

(1.河北工业大学土木与交通学院，天津 300401；2.河北工业大学土木工程技术研究中心，天津 300401)

节段拼装桥墩近年来在国内外桥梁建设中被关注，具有施工方便、节能环保和便于维护等优点[1-4]。考虑建设地域的广泛适用性，其在地震作用下的力学性能及变形特点被国内外学者所关注[5-6]，近年来发展了以配置耗能钢筋消耗能量和通过预应力筋提供一定自复位能力的无黏结预应力节段拼装桥墩。抗震变形能力是桥墩重要的抗震性能评价指标，传统(现浇)桥墩在地震荷载作用下会产生弯曲变形、剪切变形和滑移变形(纵筋拔出)，节段拼装桥墩因(干)接缝的存在，除上述外还存在接缝张开造成的变形影响，导致该类桥墩变形成分组成及占比与现浇桥墩有较大不同。

目前国内外学者对现浇桥墩整体变形成分研究表明[7-10]，现浇桥墩发生弯曲破坏时，弯曲变形对墩顶位移贡献平均可达50%以上，滑移变形平均25%～40%左右，剪切变形通常不足5%。尽管国内外对预制节段拼装桥墩的抗震性能研究较多，但对其整体地震变形成分的定量性研究涉及较少。王志强等[11]通过拟静力试验证明，预制拼装桥墩损伤主要集中于承台与桥墩间接缝处。葛继平等[12]认为节段拼装桥墩主要变形集中于接缝附近。高婧等[13]通过试验证明节段拼装桥墩墩身曲率主要集中于墩底接缝处。Z.Y.Bu等[14]试验证明在位移角达到7%时，节段拼装桥墩接缝处转动变形对墩顶位移贡献平均可达60%以上。传统的桥墩变形测量方法是采用位移计方式，位移计布置数量受到试验空间制约，且操作繁琐在试验过程中易被扰动，从而影响测量结果。数字图像相关法(Digital Image Correlation，DIC)采用无接触的测量形式，可有效避免传统接触式传感器测点少、布置难和采集困难等问题[15]。学者们在金属材料断裂和混凝土构件开裂等试验中验证了DIC技术的准确性[16-18]。笔者在无黏结预应力节段拼装桥墩拟静力试验过程中采用DIC方法，测量了水平加载过程中桥墩的空间变形及应变分布情况，进而研究桥墩各变形成分及整体变形组成，通过对桥墩整体变形分析明确了底部接缝转动等不同变形分量对墩顶水平位移的贡献。

1 试验

1.1 试件设计

4根矩形空心桥墩试件截面宽×高为450 mm×450 mm，壁厚110 mm，净保护层20 mm，每根桥墩试件由4个节段和加载端拼装而成，桥墩试件加载高度2 000 mm。试件主要参数见表1，试件尺寸和截面参数如图1所示。桥墩试件预应力筋均配置8根公称直径15.2 mm的7股钢绞线，分四孔对称布置，每孔两根。其中不锈钢钢筋试件的耗能钢筋、纵筋和箍筋均采用B1.4362不锈钢钢筋配置；普通钢筋试件的耗能钢筋和纵筋均采用HRB500E钢筋配置，箍筋采用HRB400E钢筋配置。材料力学参数见表2。

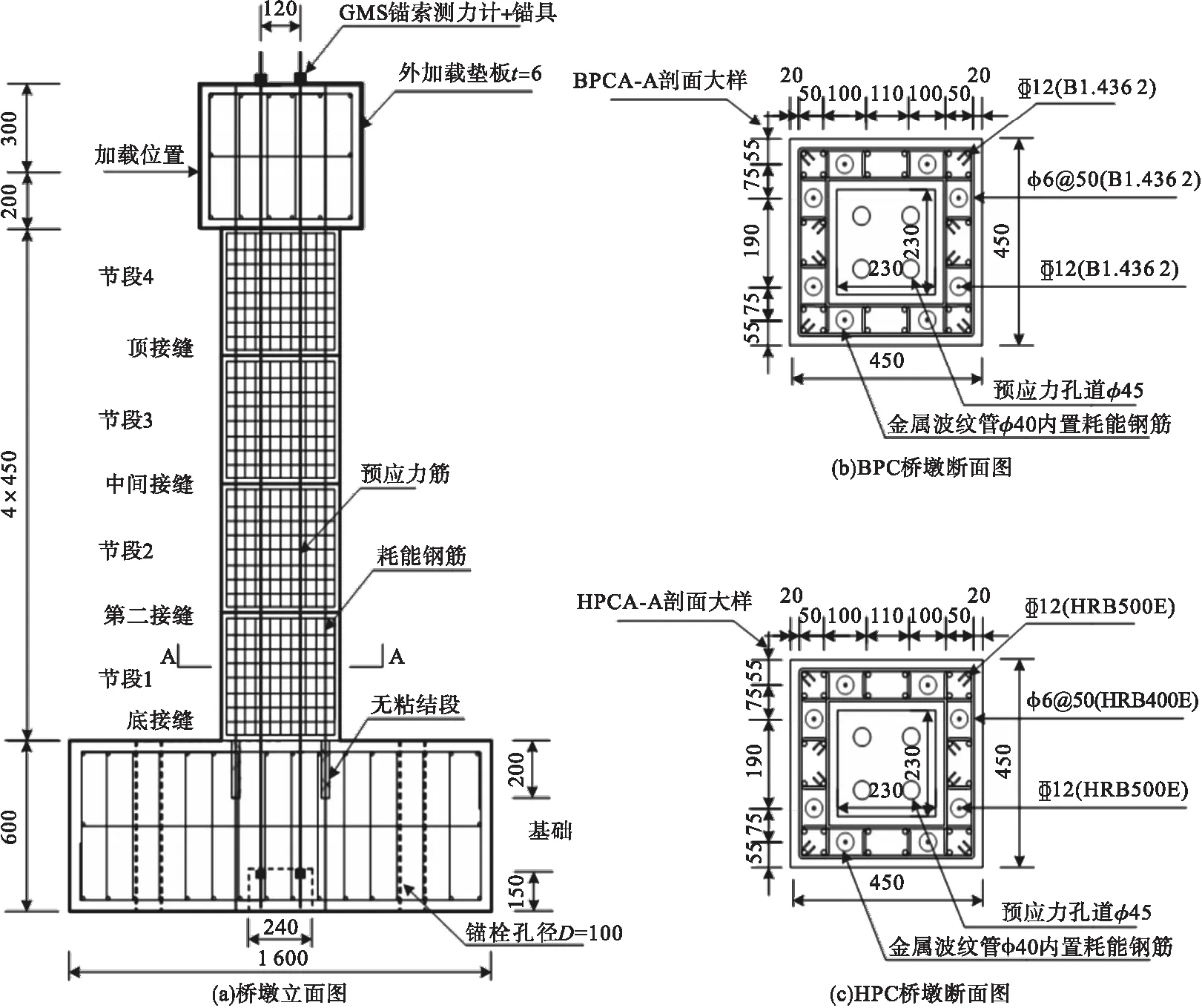
图1 试件尺寸设计Fig.1 Design size of test specimens

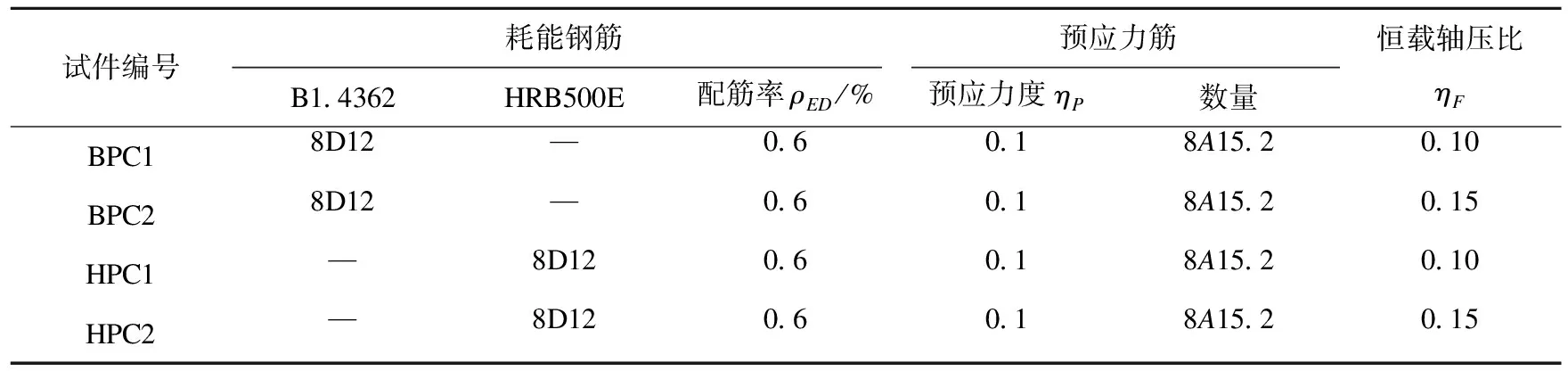
表1 试件参数Table 1 Parameters of test specimens

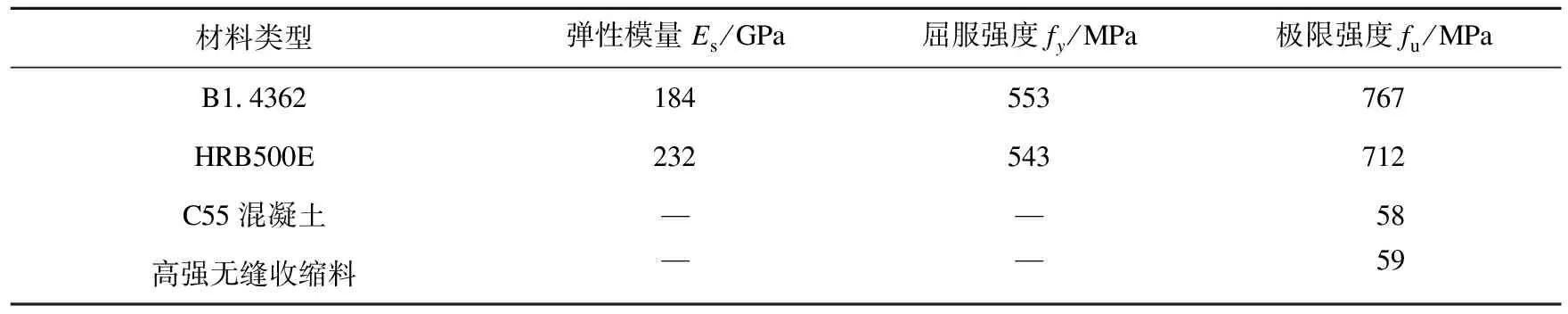
表2 材料力学性能Table 2 Mechanical properties of materials

1.2 DIC测点布设

DIC通过光照射在被检测区域的油漆散斑点图案，将其在试件加载过程中拍摄的动态图像绘制成各位置随连续帧数间变化的情况，从而观察检测区域的变形状态，其原理如图2(a)所示。本次试验中DIC测点布设见图2(b)，各标识点用于分析数据使用，标识点间距为50 mm，分布高度和分布宽度分别为600 mm和450 mm。其中分析时选取P0、P36及P72用作底接缝转动变形和墩底滑移变形分析；P7和P10、P43和P45以及P79和P81用作第二接缝转动变形和滑移变形分析，以防第二接缝处标识点由于接缝张开等无法识别及影响数据采集精度；选取P0～P11(扣除P8和P9)、P36～P47(扣除P44和P45)及P72～P83(扣除P80和P81)用作桥墩节段的弯曲变形分析；选取P37、P39及P43用作桥墩节段的剪切变形分析。

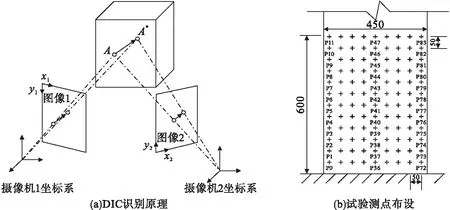
图2 DIC原理及测点布设Fig.2 Principle of DIC and layout of measuring points

1.3 试验加载制度

试验采用位移控制进行低周往复加载，每级循环3次，加载位移角依次为0.10%、0.25%、0.50%、0.75%、1.00%、1.50%、2.00%、3.00%，之后每级增加1.00%，直到试件承载力降为最大承载力85%以下。加载历程见图3。

图3 试验加载历程Fig.3 Loading displacements of specimens

2 试验结果

根据加载位移和加载端传感器记录的数据绘制各试件的力-位移关系曲线(见图4)。同时基于OpenSees建立桥墩数值模型与试验结果相佐证，模型中混凝土采用Concrete01本构模型，接缝混凝土采用ENT材料本构模型，不锈钢钢筋及预应力钢绞线采用Steel02本构模型，普通钢筋采用Reinforcing Steel本构模型。从图4可以看出，数值模拟结果与试验结果基本吻合。试件滞回曲线显示无黏结预应力节段拼装桥墩滞回曲线有较明显的捏缩现象。试件在加载初期(位移角小于1%)处于准弹性状态，没有明显的耗能和残余位移；随加载位移增大，钢筋屈服，达到试件最大承载力，试件的耗能增大，残余位移逐级增大；在位移角达到3%～4%左右，随着墩身混凝土剥落，承载力逐渐下降，预应力筋提供的自复位能力减弱。从配置的不同耗能钢筋来看，不锈钢耗能钢筋的提升了试件的最大承载力，但增大了残余位移。各试件承载力至最大承载力85%时，试件变形均能达到5%位移角。

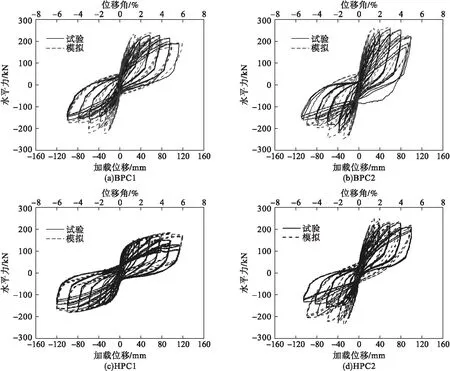
图4 试件滞回曲线Fig.4 Hysteretic curves of specimens

3 桥墩变形结果及分析

3.1 变形成分及计算原理

现浇桥墩变形成分主要以弯曲、剪切和滑移变形为主，而对于节段拼装桥墩，其接缝处张开将是主要变形成分。使用DIC测量了试件第一节段和部分第二节段在每级加载幅值处的空间变位及应变情况，图5给出了试件BPC1在位移角5%时，墩身两侧竖向应变的分布作为参考。笔者测得4根试件在加载过程中的位移及应变数据，根据数据结果对节段拼装桥墩主要变形成分进行计算。

3.1.1 接缝转动变形

接缝转动变形是指接缝张开后因截面转动引起的墩顶位移，DIC数据测得接缝数据主要以接缝竖向位移(张开高度)和压缩位移为主，接缝处截面变形计算过程见式(1)～式(3)，原理如图6所示。

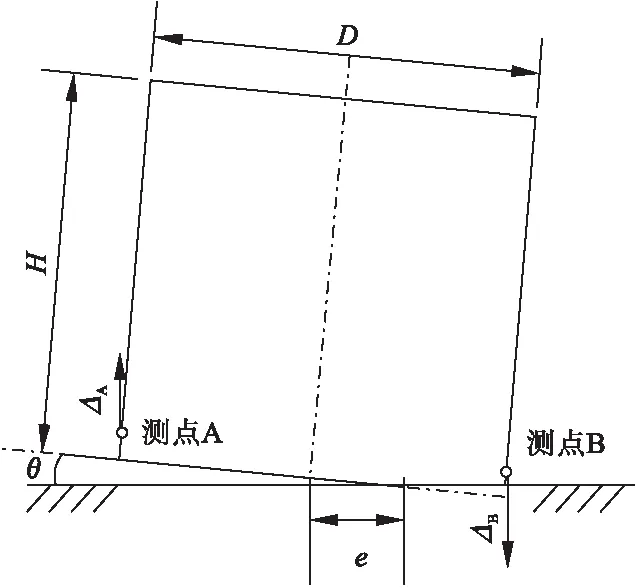
图6 接缝转动引起墩顶位移计算原理Fig.6 Calculation principle of pier top displacement by joint rotation

(1)

ΔJ=tanθ×H.

(2)

(3)

式中：ΔA和ΔB分别为测点A和测点B的竖向位移；D和H分别为截面宽度和接缝截面至墩顶高度；θ和ΔJ分别为截面转角(接缝转动)及其引起的墩顶位移；e为受压偏心距。

3.1.2 节段弯曲变形

试件的弯曲变形计算主要利用垂直试件加载方向的平面边缘及平面中轴三列标识点间的竖向切应变数据，然后计算曲率变化平均值，计算过程中要将底接缝及第二接缝处应变数据不连续的影响除去。曲率和桥墩弯曲变形计算见式(4)、式(5)，计算原理如图7所示。

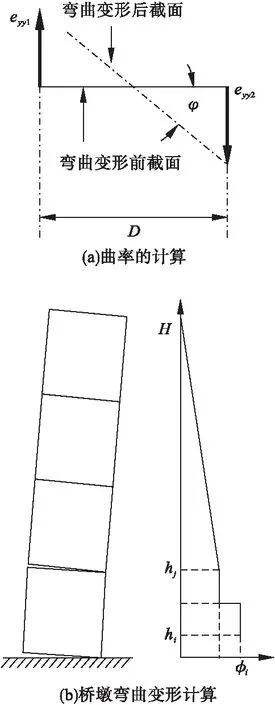
图7 曲率和桥墩弯曲变形计算原理Fig.7 Calculation principle of curvature and pier bending deformation

(4)

式中：eyy1和eyy2分别为桥墩试件受压侧和受拉侧平面标识点处的竖向应变；φ为墩身节段的曲率。

获得曲率沿桥墩高度的分布后，就可利用虚位移原理计算桥墩因弯曲引起的墩顶位移：

(5)

式中：φi为hi到hi+1区间内墩身曲率；hi和H分别为区间划分点至墩底高度和墩身高度；ΔBend为弯曲变形计算值。

3.1.3 节段剪切变形

剪切变形需要以区域内对角线长度变化所确定，DIC数据虽然能够准确地反应区域内各点位移状态，但在计算剪切变形时需要将其所含的水平和垂直拉伸(微膨胀)所产生的变形量所消除，剪切变形计算见式(6)，计算原理如图8所示。

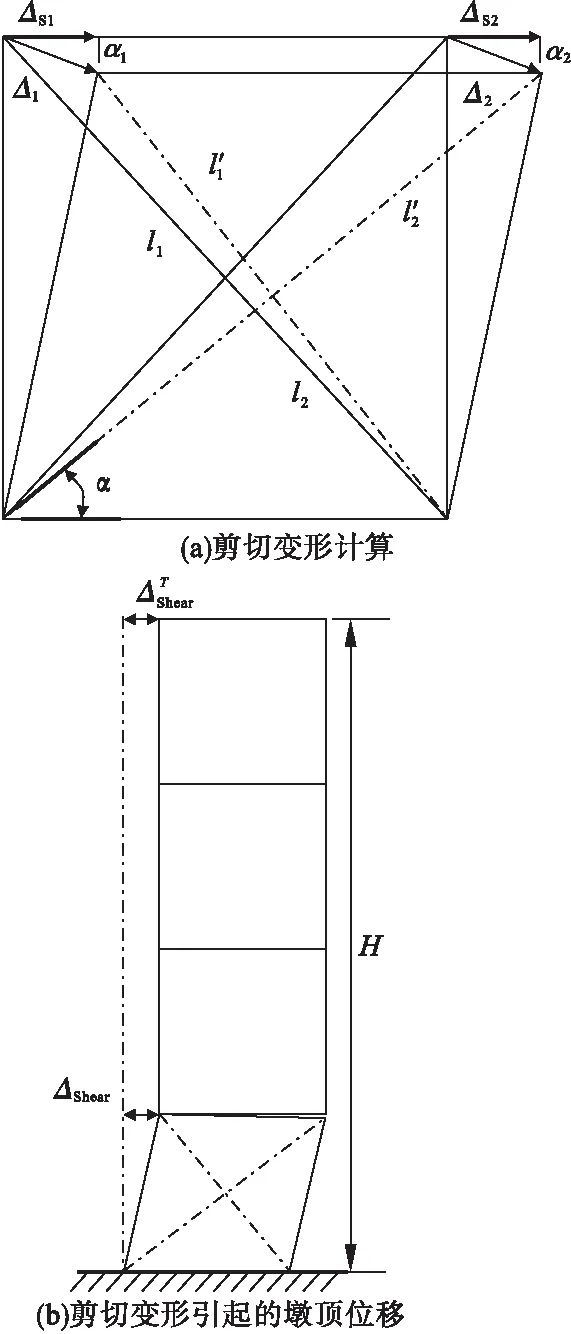
图8 剪切变形及剪切引起墩顶位移计算Fig.8 Calculation principle of shear deformation and pier top displacement by shear

(6)

剪切变形对桥墩墩顶位移的影响如图8(b)所示，由于α1与α2角度近乎为0得：

(7)

3.1.4 接缝滑移变形

接缝的滑移变形计算原理如图9所示。以底接缝为例，通过与底接缝最近的桥墩上的标示点，在加载方向上的位移的平均，减去基础的移位(采用位移计)计算得到。接缝滑移位移也等于其引起的墩顶位移。

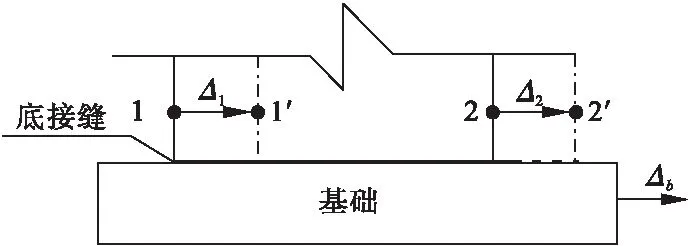
图9 滑移变形计算原理Fig.9 Calculation principle of slip deformation

滑移变形计算见式(8)：

(8)

式中：Δ1和Δ2分别为点1和点2的滑移(沿着加载方向的位移)；Δb和ΔSlip分别为基础位移计测得滑移和修正后接缝滑移变形。

上述计算都是针对底接缝描述的，当涉及的第二接缝处变形计算时，只需去除接缝下桥墩上对应最近的标示点对应的(刚体)位移即可。

3.2 预制拼装桥墩变形成分分析

依据上述算法，图10给出了各试件在加载位移水平下的接缝转动变形、桥墩节段变形(弯曲变形和剪切变形)及底接缝引起的滑移变形在总位移中的贡献率。从图中可以看出，配置不锈钢耗能钢筋试件和配置普通耗能钢筋试件在桥墩整体变形成分上没有明显差别，各变形分量占比基本一致。各试件底接缝转动变形从小位移下占比40%左右，至大位移下(位移角5%)平均占比约85%；第二接缝转动变形则会随着底接缝贡献率提升略有减小；试件的弯曲变形对于总位移贡献随位移角增大而减小，平均占比范围为5%至15%；底接缝滑移变形占比在加载前期可到10%，加载后期平均占比约5%；剪切变形则仅在试件开始加载时有3%左右的位移贡献，随位移角增大其位移贡献率不足1%。以上分析说明了节段拼装桥墩的接缝转动变形占据总位移的主要部分。节段拼装桥墩的剪切变形影响很小，这可能与试件剪跨比有关。

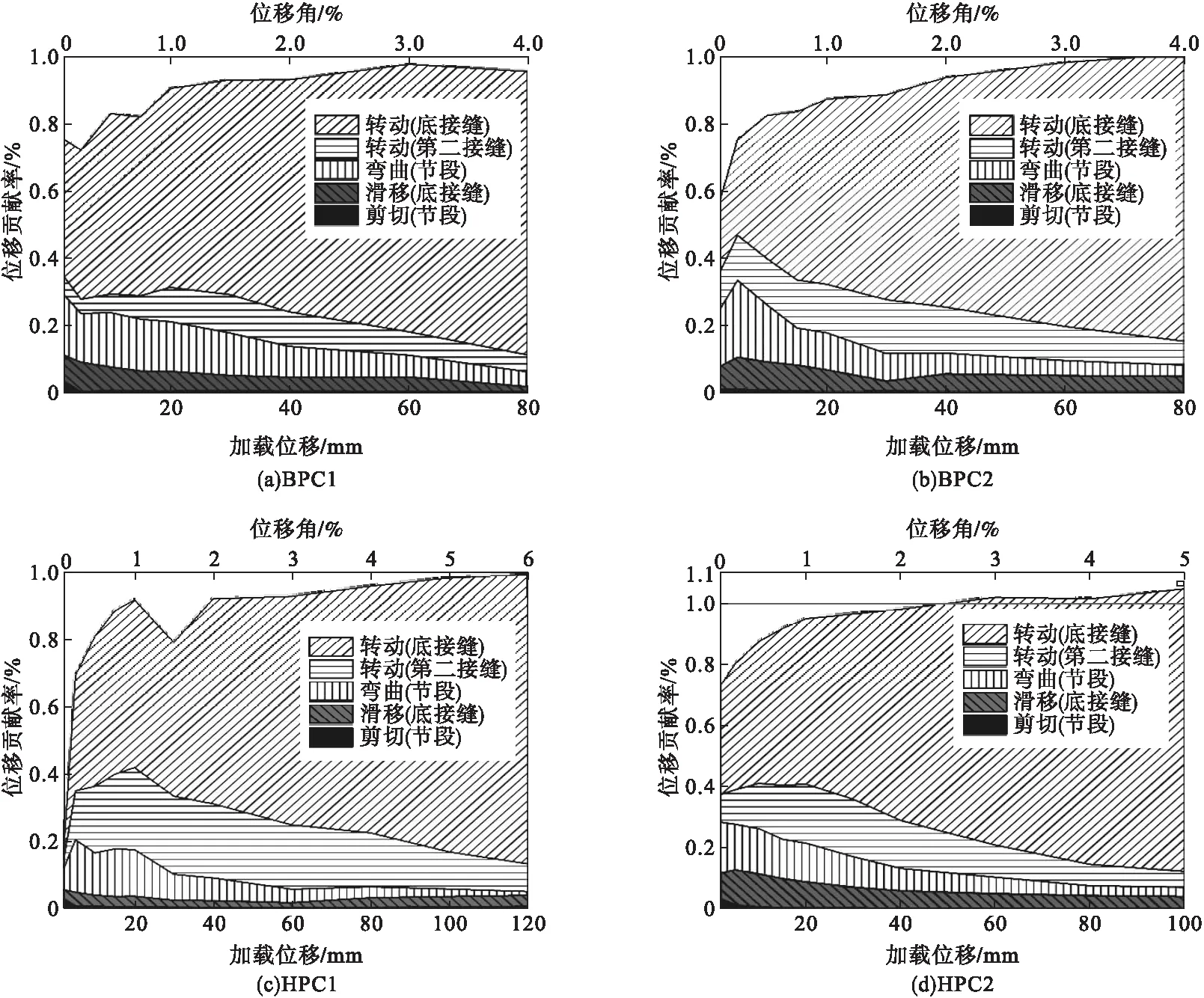
图10 桥墩整体变形Fig.10 The integral deformation of piers

由图10可以看出，桥墩整体位移和各个分项位移的计算存在少许误差，在墩顶位移角大于2%后，各变形分量对于总位移的贡献率之和接近100%(个别桥墩略大于100%，如试件HPC2)，说明DIC数据采集和变形成分计算方法是可信的。在墩顶位移较小的时候(如小于15 mm或0.75%极限位移角时)，平均误差在15%左右，原因可能是计算时更关注DIC标识区变形的影响，此时上部桥墩(节段)的弹性变形也有很大的占比，而后随着墩顶位移增长，误差最后稳定在5%～10%，甚至于更小，说明上述变形成分分析在大的变形下，可靠性更高。