新型自复位混合摇摆柱可恢复功能性能分析
2022-11-05孙祥磊
阎 石,王 涛,苏 醒,孙祥磊
(沈阳建筑大学土木工程学院,辽宁 沈阳 110168)
随着科技的发展,因地震导致房屋倒塌和人员伤亡的现象逐渐减弱,一定程度上保证了人们的生产和生活。然而,地震造成的破坏依然对国民经济和人民生活产生严重的影响。这是由于震后多数房屋自身的破坏,已经无法满足正常使用功能,且修复困难或修复经济和时间成本过高,从而导致受损房屋需要推倒重建。因此,如何解决房屋震后快速恢复功能问题意义重大。
可恢复功能结构(ERS)[1]是指在多遇地震作用或罕遇地震作用下,结构不需修复或轻微修复,即可快速恢复其使用功能。目前,ERS形式上主要包括:摇摆结构[2]、自复位结构[3]、可更换构件结构[4-5]、复合自复位结构[6]等。G.W.Housner[7]在1962年首次提出摇摆结构的概念及摇摆刚体经典模型,证明该结构具有优良的抗震性能。H.Roh[8-9]在2007年提出摇摆柱,并利用试验证明减少摇摆柱的约束可以有效降低地震加速度响应。美、日地震工程第二阶段合作研究计划会议上提出地震工程合作方向-“可恢复功能城市”[10]。美国太平洋地震工程研究中心年会[11]、第16届世界地震大会[12]等会议也都围绕“可恢复性”作为主题。由此可见,ERS已经成为地震工程研究的重点。
在摇摆-自复位结构混合体系中,毛晨曦等[13-14]提出了较多构件连接形式。其中,耗能能力较高的连接方式存在自复位能力不足的问题;而自复位能力较好的连接方式,往往耗能能力偏弱。为解决该矛盾,笔者提出了一种带有可更换软钢耗能器的新型自复位混合摇摆柱(Resilient Rocking Column with Replaceable Hysteretic Dampers,RHD-RRC),以满足“耗能高、自复位能力强、抗侧刚度适中”的目标要求。为了研究RHD-RRC的地震可恢复功能性能(Earthquake Resilient Performances,ERPs),笔者以一个高2.39 m的可恢复摇摆柱试验为例,验证了所建立的有限元模型的有效性;然后通过ABAQUS建立了RHD-RRC有限元模型,对其分别进行单调加载和低周循环往复加载,分析轴压比、耗能器厚度、预应力初始值等因素对RHD-RRC耗能能力和自复位能力的影响。通过RHD-RRC与普通摇摆柱有限元模拟结果对比分析可知,RHD-RRC的滞回曲线呈“旗帜形”,具有良好的可恢复功能能力。
1 RHD-RRC连接构造与工作原理
RHD-RRC的节点示意图如图1所示。在预制钢筋混凝土柱和基础接触面处均设有保护钢板,防止RHD-RRC在“摇摆”过程中造成混凝土压碎等现象;预留预应力筋孔道并在截面上两两对角布置,采用后张法施加预应力;耗能器通过柱和基础的预埋螺栓连接,预埋螺栓端部进行局部处理,保证“摇摆”过程中螺栓不会破坏。根据摇摆机制及地震作用下保证结构无损伤的性能指标,允许RHD-RRC产生柱脚摆动或抬升现象,然后通过耗能器耗能和柱的“摇摆”以及预应力钢筋的弹性恢复力,使RHD-RRC在地震作用下满足可恢复的目标。
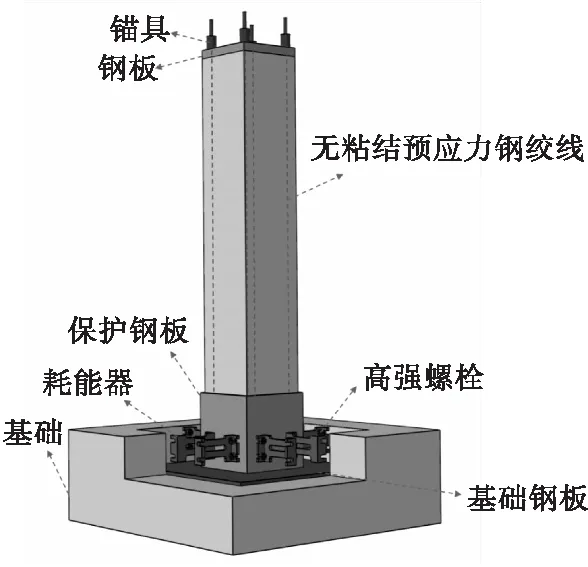
图1 RHD-RRC节点示意图Fig.1 The schematic in details of RHD-RRC joint
普通摇摆柱是通过混凝土开裂及钢筋与混凝土之间产生滑移进行耗能,耗能能力弱。RHD-RRC通过在发生大变形的柱脚部位设置耗能装置,将地震能量主要集中在耗能器上,主体结构则分担少量,以达到损伤集中、可控和保护主体结构的目的。在不影响主体结构使用功能的前提下,耗能器实现“可拆卸、可更换、易安装、快速恢复使用”的目标。通过预应力筋提供弹性恢复力,最终实现结构功能快速恢复。
RHD-RRC摇摆过程示意图如图2所示。初始状态时,柱底面接触应力分布均匀。顶部施加水平荷载后,受拉侧接触面压应力开始减小并逐渐趋向于0,受压侧压应力逐渐增大。随着水平荷载逐渐增大,柱底接触面开始减小,接触应力向受压侧集中,当全接触面达到屈服应力时,柱底最大弯矩为Mmax,RHD-RRC达到摇摆临界状态。继续增大水平荷载,RHD-RRC将会发生摇摆行为,此时摇摆柱仍然保持一定的抗倾覆能力。当重力作用线通过支撑点O′时,RHD-RRC达到临界倾覆状态[15],当变形超过这一状态,结构将发生倾覆破坏。
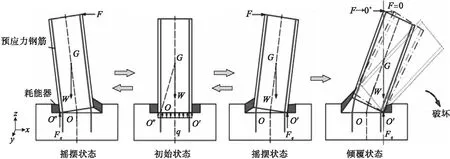
图2 RHD-RRC摇摆过程示意图Fig.2 The schematics of rocking process for an RHD-RRC
预应力钢筋为RHD-RRC提供弹性恢复力且保证其在摇摆过程中始终处于弹性状态。RHD-RRC的耗能能力由耗能器决定。笔者利用ABAQUS软件,分析轴压比、预应力初始值大小、预应力钢筋截面面积及耗能器厚度等因素对RHD-RRC抗震性能的影响。
2 有限元分析
为了验证新型自复位混合摇摆柱的可恢复功能性能,利用已有的摇摆柱试验进行有限元模型验证。然后建立一个升级的RHD-RRC有限元模型,对其进行低周循环往复加载数值模拟,分析不同参数对其可恢复功能性能的影响。
2.1 模型验证
为了验证所建立的有限元模型准确性,选用Y.Liu等[14]完成的新型可恢复摇摆柱的工况S20-5.5-0.1-AR试验结果进行对比。材料参数见表1,模拟结果如图3和图4所示。图中,F为构件的水平承载力;Δ为柱顶位移;θ为不同柱顶位移对应的转角。
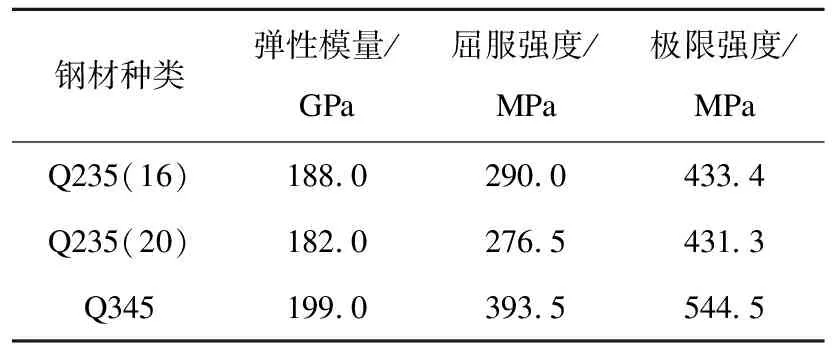
表1 材料性能试验结果Table 1 Test results of material properties
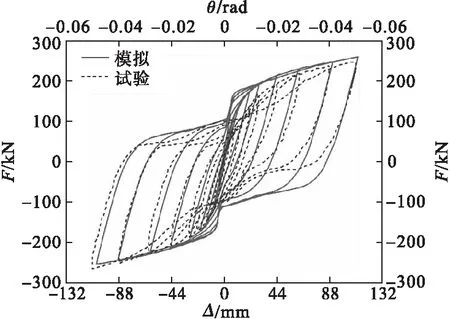
图3 试验-模拟滞回曲线对比Fig.3 Comparison of experimental and simulated hysteretic curves
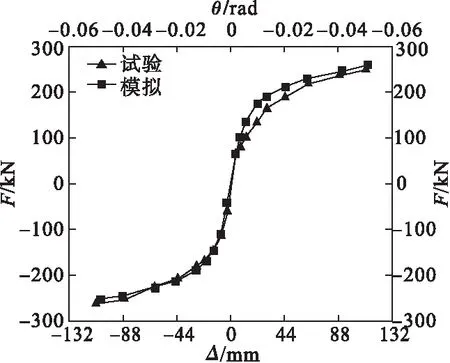
图4 试验-模拟骨架曲线对比Fig.4 Experimental-simulated skeleton curve comparison
从图3、图4可以看出,该摇摆柱具有足够的耗能能力,但自复位能力差,具有较大的残余变形。由于构件的各个接触面在加载过程中均考虑了相对滑移,数值模拟结果与试验数据吻合良好,两者且均出现“捏缩”现象。由于数值模拟中的材料参数、加载方式、边界条件相对试验更加理想化,因此滞回曲线相对更加饱满。模拟结果和试验结果吻合度高,整体趋势基本相同,可以正确反映试验工况对应的水平承载力以及耗能能力等力学性能,验证了有限元模型的准确性。
2.2 RHD-RRC有限元模型的建立
在ABAQUS中,对新型自复位混合摇摆柱进行拟静力加载下的滞回性能分析。摇摆柱长×宽×高为400 mm×400 mm×1 600 mm,基础长×宽×高为1 600 mm×1 600 mm×500 mm,混凝土强度等级为C30,混凝土采用文献[16]附录C中本构关系。预应力钢筋简化为理想的弹性材料。其他钢筋及钢材的本构关系均采用两折线随动强化模型。
2.3 加载模式
根据轴压比、预应力初始值大小、预应力钢筋截面面积及耗能器厚度的不同,共设计5种工况(见表2)。采用转角(位移)控制加载方案,加载制度见图5。
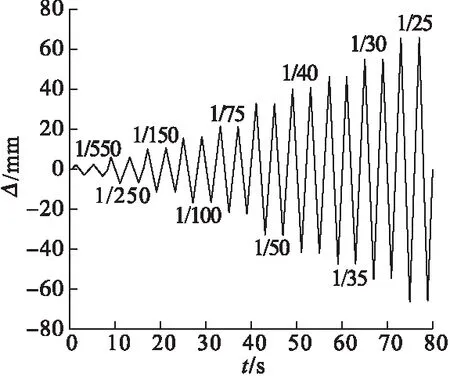
图5 水平往复荷载位移控制制度Fig.5 The displacement control scheme of horizontal reciprocating loading

表2 数值模拟工况设计Table 2 The design of numerical simulation cases
3 模拟结果分析
3.1 三种摇摆柱模拟结果对比
自复位混合摇摆柱与普通摇摆柱相比,其工作过程存在四种机制:摇摆机制、自复位机制、集中耗能机制、可更换构件机制[6]。而普通摇摆柱仅存在其中一种或多种机制。
对于摇摆机制,自复位混合摇摆柱与普通摇摆柱均改变了上部结构与基础之间的约束,并由弯剪变形模式改为整体抬升的摇摆模式,从而避免了构件的损伤,使结构具有一定的可恢复能力。对于自复位机制,自复位混合摇摆柱具有良好的自复位能力,而文献[14]中设计的性能可恢复摇摆柱,具有良好耗能能力的同时,其自复位效果不理想,在地震作用下,无法满足结构自复位的目标。对于集中耗能机制,是可恢复功能结构的核心机制之一。自复位混合摇摆柱将地震能量集中于柱脚的耗能器中,因此,主体结构可以达到无损伤的设计目的。对于普通框架柱和普通摇摆柱,其耗能主要是混凝土开裂进行耗能,后期修复困难。对于可更换构件机制,是可恢复功能结构的另外一个核心机制。自复位混合摇摆柱通过更换柱脚处的耗能器,降低了影响结构正常使用功能时间,实现“可拆卸、可更换、易安装、快速恢复使用”的目标。
为进一步研究预应力钢筋与软钢耗能器对摇摆柱耗能与自复位性能的影响,采用三种类型的摇摆柱进行对比分析。第一种为普通摇摆柱(RRC),摇摆界面处仅设有预应力筋,其他参数均与RHD-RRC相同;第二种仅设有耗能器的摇摆柱(RHD),不设置预应力钢筋,其他参数均与RHD-RRC均相同;第三种为RHD-RRC。通过各个滞回曲线面积下的累积耗能系数及等效黏滞阻尼系数hc[17]来表示其耗能能力。
三种摇摆柱的塑性变形主要发生在摇摆截面处,其他部位均处于弹性状态,摇摆柱本身未出现损伤情况。三种摇摆柱的滞回曲线、骨架曲线、等效黏滞阻尼系数hc及累积滞回耗能系数ξ对比结果如图6~图9所示。
从图6~图9可以看出,对于耗能能力,RRC无残余变形,耗能主要依靠混凝土塑性变形。RHD-RRC和RHD滞回曲线表明,耗能软钢发挥了很好的耗能能力。随着荷载幅值的增加,RHD-RRC和RHD的滞回环面积不断增大,耗能能力进一步提高。当达到峰值荷载后,RRC和RHD-RRC均出现了强度退化现象,RRC退化速度更快,承载力较低。三种摇摆柱的hc-θ曲线走势基本相同,呈现平稳上升的趋势,随着θ增大,摇摆柱塑性变形越大,耗散地震能量越多。当θ<0.005时,三种摇摆柱的累积耗能曲线基本保持重合状态,随着θ增大,三条曲线开始分离,耗能器的有无对三种摇摆柱的累计耗能影响逐渐增大。
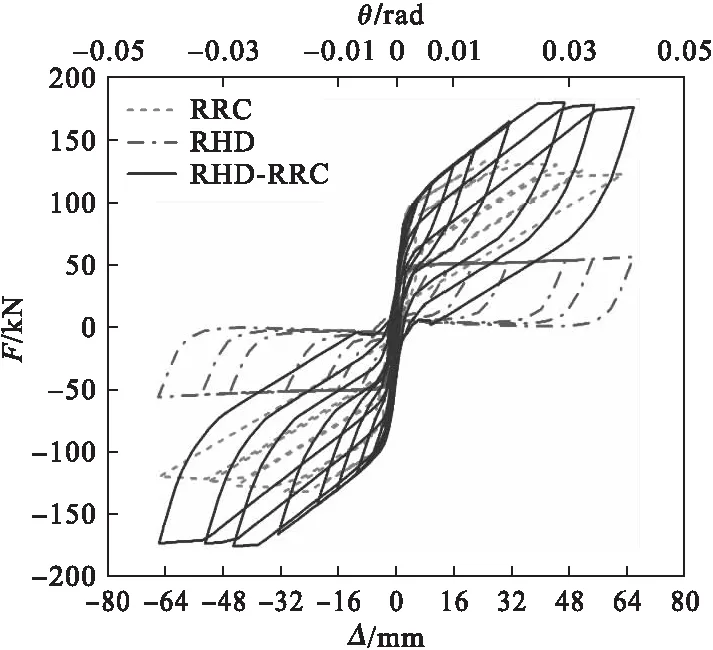
图6 滞回曲线对比Fig.6 Comparison of hysteretic curves

图7 骨架曲线对比Fig.7 Correlation of skeleton curve of RRC,RHD and RHD-RRC

图8 等效黏滞阻尼系数hc对比Fig.8 Equivalent viscous damping coefficients hcof RRC,RHD and RHD-RRC
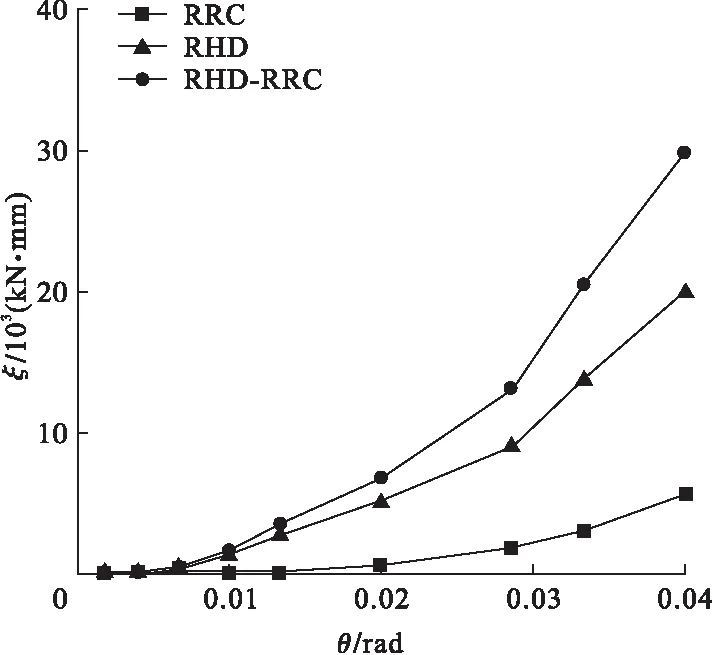
图9 累积耗能系数ξ对比Fig.9 Cumulative energy dissipation coefficient ξof RRC,RHD and RHD-RRC
RHD-RRC相比于RRC和RHD而言,具有良好的耗能能力及自复位能力,强度退化和刚度退化速度较慢,具有RRC和RHD的优点,性能指标最好。
3.2 不同参数对RHD-RRC抗震性能的影响
3.2.1 预应力筋截面面积
笔者以工况1和工况2为例,研究预应力筋截面面积对RHD-RRC的可恢复功能性能影响。滞回曲线、骨架曲线、累积滞回耗能系数ξ曲线如图10~图12所示。
从图10~图12可以看出,在其他参数相同的前提下,增大预应力筋截面面积,两种工况下的滞回曲线都比较饱满,RHD-RRC抵抗水平荷载的能力进一步提高,有刚度退化现象。
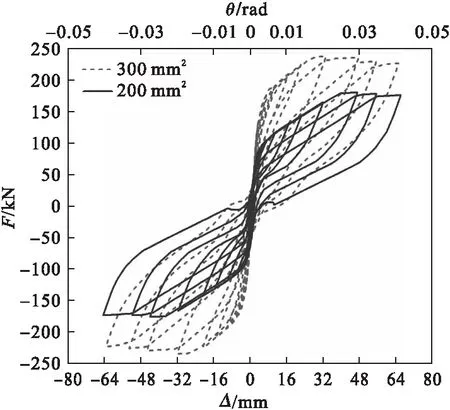
图10 预应力筋截面积对滞回曲线的影响Fig.10 Influence of prestressed rebar cross-sectional areas on hysteretic curves
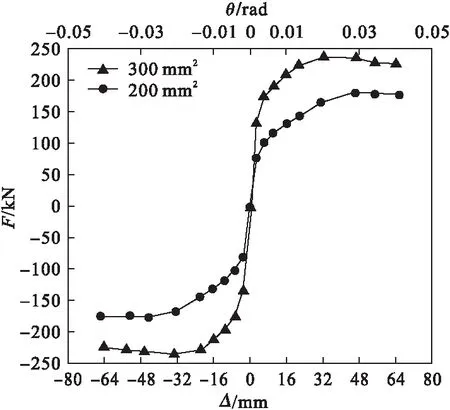
图11 预应力筋截面积对骨架曲线的影响Fig.11 Influence of prestressed rebar cross-sectional areas on skeleton curves
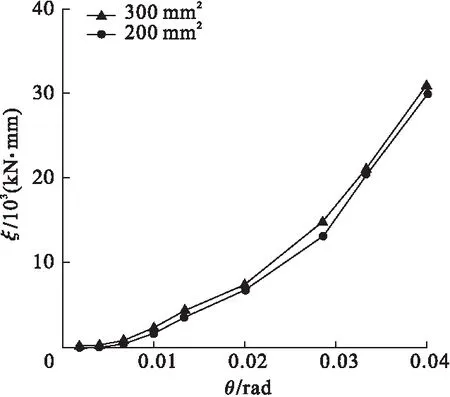
图12 预应力筋截面积对累积耗能系数的影响Fig.12 Influence of prestressed rebar cross-sectional areas on cumulative energy consumption coefficient
由于在初始预应力相同的条件下,不同截面面积的预应力筋提供的弹性恢复力随着θ的增大而增大,混凝土开裂产生的耗能降低。由于耗能器的参数均相同,因此两种工况的累积耗能基本相同。
3.2.2 预应力初始值
笔者以工况1和工况3为例,研究预应力初始值对RHD-RRC可恢复功能性能的影响。滞回曲线、骨架曲线、累积耗能系数ξ曲线如图13~图15所示。
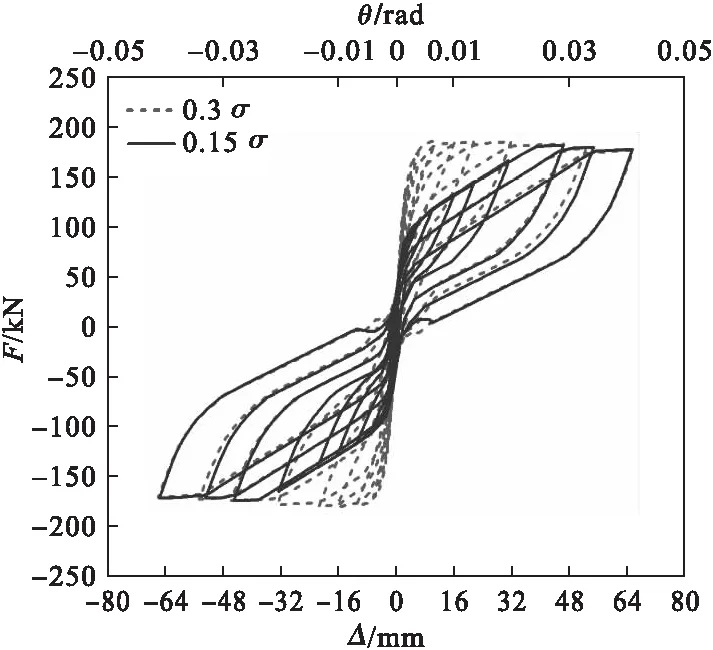
图13 预应力初始值对滞回曲线的影响Fig.13 Influence of different initial prestress levels on hysteretic curves
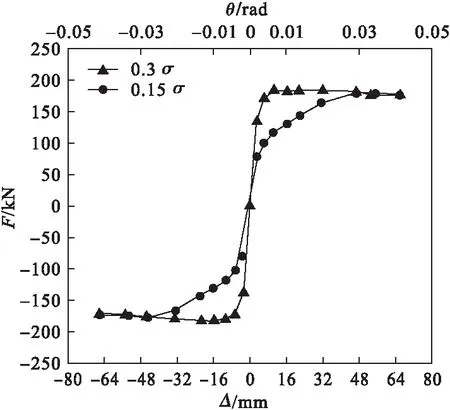
图14 预应力初始值对骨架曲线的影响Fig.14 Influence of different initial prestress levels on skeleton curves
从图13~图15可以看出,在其他参数均相同的前提下,提高预应力初始值,可以有效提高RHD-RRC的前期抗侧能力和一定的自复位能力,且滞回环比较饱满。随着θ的增大,两种工况的水平抗侧能力逐渐趋于一致,刚度退化几乎相同。当预应力钢筋在弹性段时,预应力初始值较小时的摇摆柱具有更好的耗能能力,分析原因是预应力初始值较大会限制混凝土的开裂的缘故。当钢筋到达塑性段时,两种工况下RHD-RRC的耗能能力趋向于相同。由于耗能器的参数均相同,因此两种工况的累积耗能能力基本相同。

图15 预应力初始值对累积耗能系数的影响Fig.15 Influence of different initial prestress levels on cumulative energy consumption coefficient
3.2.3 轴压比和不同耗能器厚度
文献[14]中对性能可恢复摇摆柱的轴压比和不同耗能器厚度的影响进行了相关研究,笔者在此基础上,研究轴压比和不同耗能器厚度对RHD-RRC自复位能力和耗能能力的影响。滞回曲线和骨架曲线如图16~图19所示。
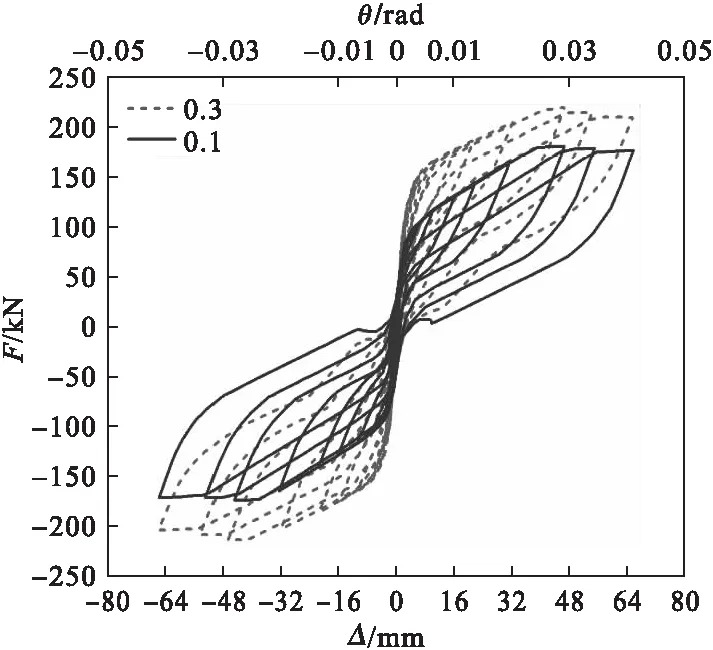
图16 轴压比对滞回曲线的影响Fig.16 Influence of axial compression ratio on hysteretic curves
从图16和图17可以看出,两种轴压比下RHD-RRC的滞回曲线都很饱满,都具有较好的耗能能力。随着轴压比的增大,RHD-RRC的水平抗侧能力提高,即轴压比和RHD-RRC的整体刚度呈正比关系,刚度退化能力降低。两种工况下骨架曲线走势基本相同,呈现平稳上升的趋势。增大轴压比,导致混凝土柱受压开裂,此时耗能能力由耗能器和混凝土开裂共同组成。两种工况下累积耗能差别不大,是因为耗能主要集中在耗能器中,与轴压比有一定的相关性。
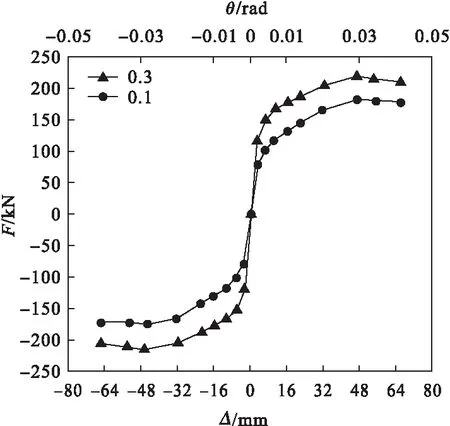
图17 轴压比对骨架曲线的影响Fig.17 Influence of axial compression ratio on skeleton curves
从图18和图19可以看出,两种工况下RHD-RRC在双向加载过程中都有弹性阶段和塑性阶段。滞回曲线的走势具有一致性,且滞回环比较饱满,具有较好的耗能能力。随着耗能器厚度的增加及θ的增大,RHD-RRC的水平抗侧能力增大,自复位能力降低,刚度退化速度降低,且耗能能力与耗能器厚度呈正比例关系。等效黏滞阻尼系数及累积耗能系数均与阻尼厚度呈正比例关系。
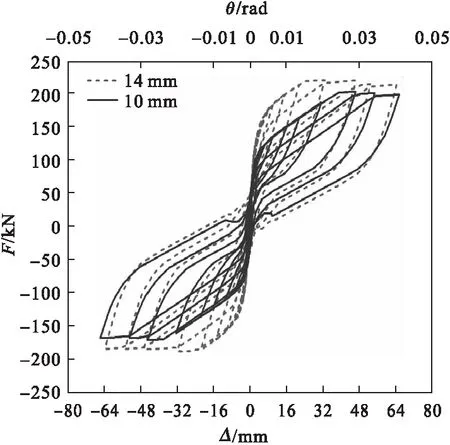
图18 耗能器厚度对滞回曲线的影响Fig.18 Influence of energy dissipator thickness on hysteretic curves
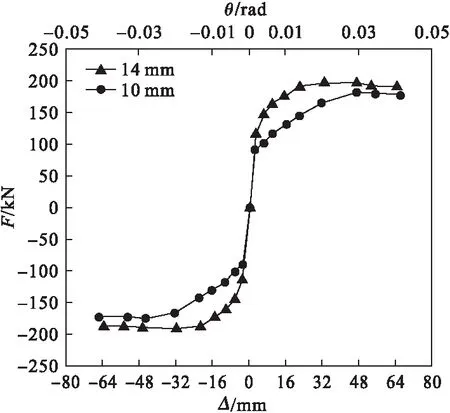
图19 耗能器厚度对骨架曲线的影响Fig.19 Influence of energy dissipator thickness on skeleton curves
4 结 论
(1)RHD-RRC连接构造设计简单且分工明确。预应力钢筋提供弹性恢复力,耗能器高效耗能,可以实现“可拆卸、可更换、易安装、快速恢复使用”的目标。
(2)RRC无残余变形,耗能主要依靠混凝土塑性变形;RHD的滞回曲线形状具有高度的一致性,饱满且平滑,耗能能力更高;HRD-RRC同时具有良好的自复位能力和耗能能力,耗能主要集中在耗能器中,避免了混凝土构件的损伤。
(3)RHD-RRC的自复位能力及耗能能力主要由预应力筋和耗能器决定,轴压比也有一定的影响。提高初始预应力或增大预应力筋截面面积,会提高RHD-RRC的自复位能力,不同耗能器厚度对RHD-RRC的耗能能力也呈正相关。在设计或使用时,应考虑耗能器的厚度及预应力大小的匹配问题。
