浅埋盾构掘进诱发土体剪胀对地表变形的影响分析

叶友林，路志旺,孙雅珍，商诗健,钱子杰

(1.沈阳建筑大学土木工程学院，辽宁 沈阳 100168；2.沈阳建筑大学交通与测绘工程学院，辽宁 沈阳 100168)

近年来，为充分利用城市地下空间，浅地层盾构开挖已日趋普遍。盾构施工不可避免会对隧道周围土体产生扰动，特别是在黏聚力微弱的砂土地层，稍有不慎就会发生地表沉降。因此，有必要探究施工和土体参数机制对地表变形的影响。R.B.Peck[1]基于大量监测数据发现，地表横向沉降槽与高斯曲线具有高度相似性，给出了预测地表横向沉降槽的经验公式。P.B.Attewell 等[2]在R.B.Peck研究的基础上，提出了纵向沉降槽的估算应以高斯累积分布的形式进行。然而传统经验公式的计算存在过多简化，忽略了盾构和土体参数因素对地表变形的影响。后续学者借助室内模型试验[3-6]和数值模拟[7]探究了砂土地层各参数间的影响，并对传统经验公式进行了修正。

实际盾构掘进过程中，隧道周围土体会发生剪切破坏，而这种破坏表现为土体的剪胀或剪缩。隧道周围及地表以下土体受剪胀作用的影响发生不同程度的体积变化，进而影响地表变形。大量研究表明，剪胀角在调控塑性区体积应变大小方面发挥显著作用。杨小礼等[8]假定在塑性屈服过程中剪胀角恒定，基于数值模拟，探讨了土体剪胀对隧道围岩塑性区的分布以及最大剪切应变速率的影响。P.F.Li等[9]基于非关联流动准则(剪胀角小于内摩擦角)分析了砂土地层土体剪胀对隧道开挖面极限支护压力的影响。孙田[10]则从细观角度分析了盾构掘进过程中砂土剪胀对盾构推力的影响。

上述关于土体剪胀的研究主要集中于隧道面稳定方面，而对于地表变形的研究相对局限。基于此，笔者利用三维数值模拟软件FLAC3D建立了以沈阳地铁一号线某段隧道为例的有限差分模型，探讨了盾构掘进过程中，砂土剪胀作用下工作面支护压力、隧道埋深对地表变形的影响，并采用无量纲参数对最大地表沉降进行了修正。将有限差分模型预测结果、经验公式修正值、现场实测数据进行对比分析，揭示了砂土地层浅埋盾构隧道施工地表沉降的变化规律。

1 基本原理

1.1 地表横向沉降的经验预测法

早期人们利用大量经验法和半经验法来预测地表变形，其中最著名的是peck经验法。通过大量实测数据分析，得出地表的横向变形满足高斯曲线分布(见图1)，计算如下：

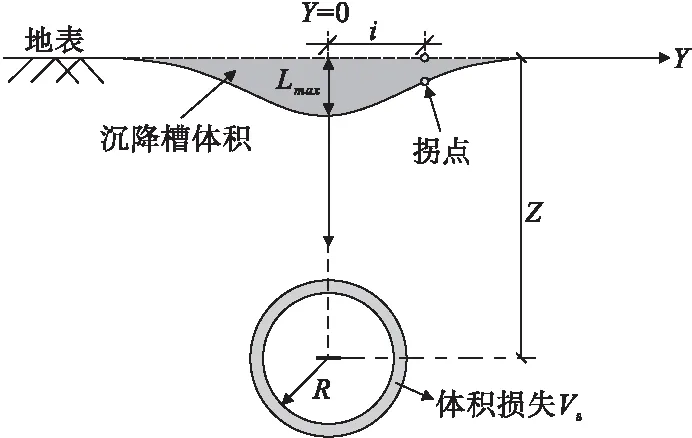
图1 地表横向沉降槽示意图Fig.1 Schematic diagram of a lateral surface settlement trough

(1)

(2)

VS=4V1πR2.

(3)

(4)

式中：Y为距隧道轴线的水平间距；L(Y)为距隧道轴线Y处的地表变形值；Lmax为隧道轴线处的地表变形值；i为地表沉降槽的宽度(隧道中轴线到曲线拐点的距离)；V1为地面体积损失率；Vs为隧道单位长度的土体体积损失量；φ为土体内摩擦角；Z为隧道中轴线处的埋深。

M.P.O′Reilly等[11]从隧道埋深的角度，提出了沉降槽宽度与隧道埋深以及地层条件之间的关系式：

i=KZ.

(5)

式中：K为考虑地层条件的经验常数，对于砂土，取值为0.2～0.3，对于黏性土，取值为0.5～0.6。

1.2 非关联流动准则

砂土在受剪屈服过程中，其体积的变化受土体剪胀角ψ的调控，所以在分析地表变形问题中，剪胀角对地层稳定存在一定的影响。当土体剪胀角等于摩擦角时则土体服从相关联流动准则，否则服从非关联流动准则。定义剪胀系数η=ψ/φ，其中φ为土体内摩擦角。当0≤η<1且土体服从Mohr-Coulomb屈服准则时需对土体强度参数c*和φ*进行修正[12]：

(6)

(7)

式中：c为土体黏聚力。

2 数值模型的建立

2.1 工程背景

笔者以沈阳地铁1号线重工街—启工街某段圆形隧道盾构施工为背景，建立考虑盾构掘进的三维数值模型。盾构外径为6.2 m，盾构区间采用标准的衬砌管片，衬砌外径为6 m，内径为5.3 m，环宽1.2 m，区间覆土厚度为7.86～13.723 m。盾构掘进地层主要有粉砂、中沙、粗砂和砾砂。掘进地质断面如图2所示。

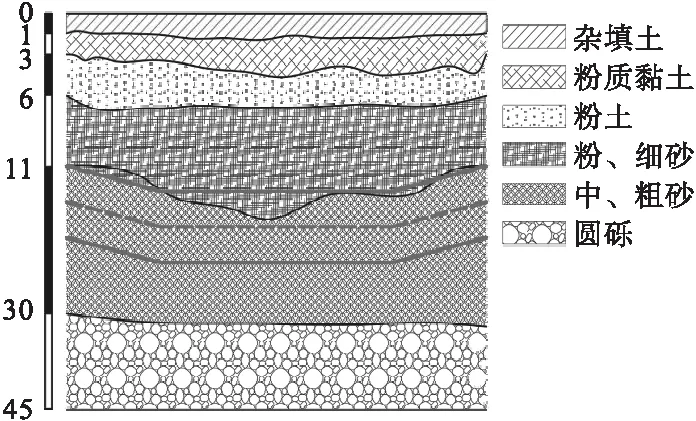
图2 地质断面图Fig.2 Geological cross-sections

2.2 模型的建立与边界条件的确定

基于三维显式有限差分程序FLAC3D进行数值模拟，不考虑地面附加荷载和地下水的影响，通过逐步开挖的方式模拟盾构掘进。模型边界依据应力释放后围岩土体的应力与位移的变化在3D(D表示隧道直径)以外约小于5%，5D以外约小于1%进行确定[13]，故本模型横向边界距隧道轴线近似取为5D，模型的底面在X、Y、Z三个方向上都是固定的。垂面在X方向上是固定的，前后侧平面Y方向固定，模型顶面X、Y方向均为自由面(见图3)。

图3 模型建立及网格划分Fig.3 Modeling and mesh generation

2.3 模型材料及参数

土层材料假定为各向同性，并服从摩尔-库伦准则的弹塑性行为和非关联流动规律，数值分析中所采用的土体参数见表1。混凝土衬砌采用具有弹性行为的实体单元，盾尾空洞注浆和由于超挖导致的地层损失统一考虑为均质等厚的圆形截面区域并定义其为等效层[14]，等效层的厚度取值直接定为盾构外径与隧道衬砌外径的间距，不考虑盾构姿态调整产生的土体损失。其材料属性也具有连续均质的弹性行为，弹性模量取2 MPa。盾构机的模拟采用壳单元进行模拟，材料为具有各向同性的线弹性材料，具体参数见表2[15]。

表1 土层参数Table 1 Parameters of soils

表2 衬砌、注浆及盾构机参数Table 2 Parameters of lining,grouting and shield machine

3 地表变形分析

3.1 砂土剪胀对地表变形的影响

笔者采用剪胀系数η进行分析，取值分别为0、0.5和1。并设定掌子面支护压力为Pu，其计算式如下：

Pu=k0σz.

(8)

k0=1-sinφ.

(9)

式中：k0为土体侧压力系数；σz为开挖面中心点处土体重力。

图4为隧道埋深比为1、掌子面支护压力为Pu时，三种剪胀系数下的地表纵向变形曲线。由图4可知，土体剪胀对掌子面后方地表变形影响较大，且当剪胀系数大于0.5时，对地表变形的影响逐渐减小。图5为隧道埋深比为1、掌子面支护压力为Pu时，三种剪胀系数下的地表横向变形曲线。由图5可知，相比于隧道轴线处的最大地表沉降，剪胀系数的增大，对横向沉降槽的宽度以及隧道轴线两侧地表变形的影响并不是很大。故在实际工况中，考虑土体剪胀对地表变形的影响时，应重点关注隧道轴线处的地表最大沉降。

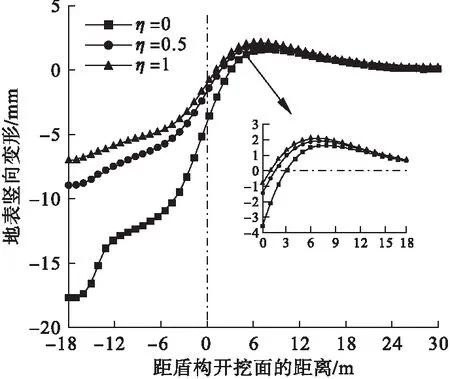
图4 不同剪胀系数下纵向地表变形曲线Fig.4 Longitudinal surface deformation curves for different dilatation factors

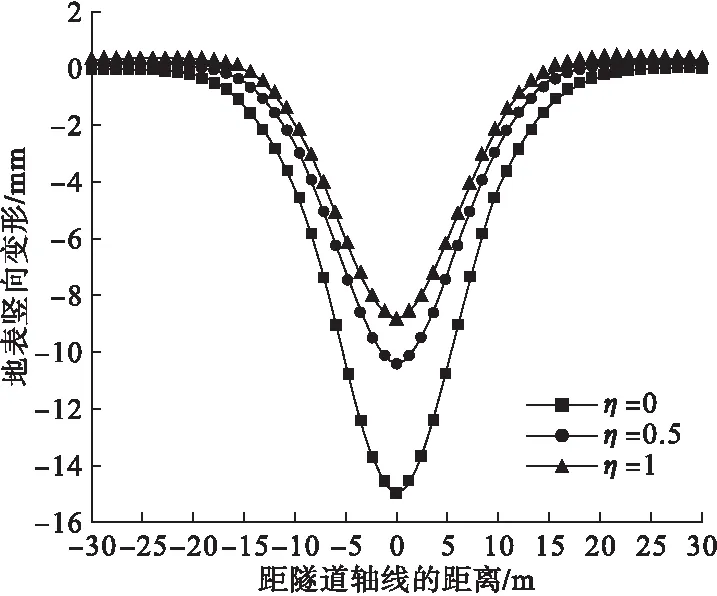
图5 不同剪胀系数下横向地表变形曲线Fig.5 Transverse surface deformation curves for different dilatation factors

3.2 考虑剪胀作用下掌子面支护压力对地表变形的影响

定义λ=P/Pu，其中P为盾构掘进时施加在掌子面的支护压力，λ为支护压力比。分别取λ为0.4、0.7、1、1.5和2.5进行分析。

图6为隧道埋深比为0.5时，五种支护压力比下的地表横向变形曲线。由图6可知，随着支护压力的增加，地表最大沉降量增加。图7为不同支护压力比下，剪胀系数分别为0、0.5、1时的地表最大沉降柱状图，图中给出了三种剪胀系数下的拟合曲线。由图7可知，当λ≤1时，三种剪胀系数之间相对差值基本一致；当λ>1时，随着支护压力比的增大，相对差值逐渐增大，且三种剪胀系数下的拟合曲线均表现为随支护压力比的增大而增长的趋势，地表最大沉降受剪胀作用的影响随支护压力比的增大而逐渐增加。所以在实际工况中应合理设定支护压力比，减小因土体剪胀而对地表变形产生的影响。

图6 不同支护压力比下横向地表变形曲线Fig.6 Transverse surface deformation curves for different support pressure ratios

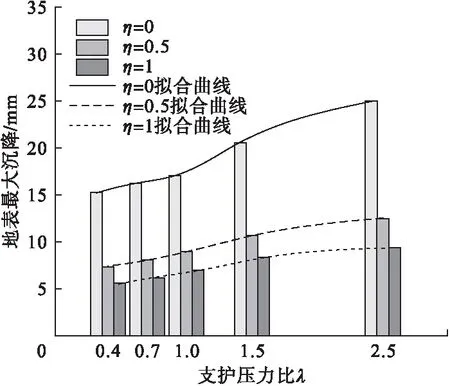
图7 地表沉降-支护压力比柱状图Fig.7 Histogram of surface settlement-support pressure ratio

3.3 考虑剪胀作用下隧道埋深对地表变形的影响

笔者以埋深比(H/D)分别为0.5、1、1.5和2为工况，研究掌子面支护压力为Pu，其他条件不变的情况下，砂土剪胀作用下隧道埋深对横向地表变形的影响。图8为隧道在不同埋深下的横向地表沉降曲线。由图可知，地表的最大沉降发生在隧道轴线处，且向两边逐渐减小。随着隧道埋深比的增加，地表最大沉降逐渐减小，沉降槽的宽度逐渐增大，形状从窄而深渐渐转化为宽而浅。但当左右距离隧道中轴线为D时，地表沉降规律发生突变，随着隧道埋深的增加，地表沉降逐渐增大。

图8 不同埋深比下横向地表变形曲线Fig.8 Transverse surface deformation curves at different burial depth ratios

图9为不同埋深比下，剪胀系数分别为0、0.5、1时的地表最大沉降柱状图。由图可知，同一埋深下，砂土剪胀作用抑制了最大地表沉降的增长。随着隧道埋深比的增加，土体剪胀作用对地表沉降的影响逐渐减小。

图9 地表沉降—埋深比柱状图Fig.9 Histogram of surface settlement-depth of burial ratios

图10为H/D为0.5、1、1.5和2时，三种剪胀系数所对应的土体体积应变增量云图。由图可知，当H/D=0.5、η=0时，体积应变增量的变化主要发生在隧道拱顶至地表的区段，并延伸到了地表，隧道拱腰处的体积应变增量的变化并不明显。H/D=0.5、η=0.5时，最大体积应变增量的变化区域由隧道拱顶转移到了隧道的拱腰处，但拱顶至地表区段仍存在体积应变增量的变化区，且该区段逐渐趋近于隧道的中轴线位置处，在靠近地表区段以尖角的形式出现，说明剪胀系数的增大，对隧道轴线处的地表最大沉降有较大影响。当H/D=0.5、η=1时，最大体积应变增量的变化区仍在隧道的拱腰处，拱顶处的体积应变增量的变化区域被截留到了隧道的周围，并未延伸到地表。表明当剪胀系数过大时，高估了土体的自稳定性。随着隧道埋深的增加，体积应变增量变化区对地表的影响逐渐减小。当H/D≥2时，无论考不考虑土体剪胀作用，隧道掘进土体体积应变增量的变化区均集中到了隧道拱腰处，拱顶处并未发生变化，这可能是因为土体埋深比达到一定值后，由于隧道拱顶以上土体的自重，土体颗粒更加密实，拱顶以上区段受土体剪胀作用的影响几乎可以忽略。

图10 土体体积应变增量云图Fig.10 Contour plots of soil volume strain increment

3.4 横向地表沉降经验公式的修正

基于数值模拟的预测可以得到砂土剪胀作用影响地表土体体积的变化，且直观反应为隧道轴线处的最大地表沉降。剪胀系数在取值大于0.5时，对地表变形的影响较小，结合文献[16]对剪胀角取值的论述，将剪胀系数η的取值设定为0～0.5。采用无量纲参数β对纵横向地表沉降经验公式进行修正，考虑到β的取值受剪胀系数的影响，将β的取值初步拟定为0～0.5。

对于横向沉降公式的修正，笔者仍按照经典的peck曲线进行预测，但考虑到地表沉降受土体剪胀效应的影响，将掘进稳定后的最大沉降以无量纲参数β进行修正，计算如下：

(10)

式中：β为无量纲参数。

4 工程验证

笔者基于沈阳地铁1号线工程实测数据，对隧道埋深为11.5 m(小于2D)和13.4 m(大于2D)的地表横向沉降进行分析，基于文献[7]中对不同地质条件下的地层损失进行的论述，取地层损失率V1=1%，经验常数K为0.2～0.3。将数值结果与实测数据进行对比，结果如图11所示。监测点的布置以及详细的测量数据参考文献[17]。考虑到隧道监测断面的设置距离在20～50 m，无法形成完整的数据对比，故不在此进行地表纵向变形的讨论。

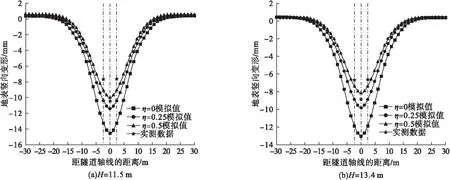
图11 横向地表变形曲线Fig.11 Transverse surface deformation curves

由图11可知，随着隧道埋深的增加，实测地表沉降逐渐减小，但变化量并不是很大，这也验证了文中所得结论正确。通过实测值与模拟值对比可以看出，在不考虑剪胀作用的情况下，模拟值明显大于实测值；当考虑剪胀作用时，随着剪胀系数的增大，二者的差值表现为先减小后增大。这也说明了过大的剪胀系数会高估地表的稳定性。但两隧道埋深下，隧道轴线处的实测值均处于剪胀系数η=0.25和η=0.5之间，只是随着隧道埋深的增加，实测值逐步靠近η=0.25处。可以说明，随着隧道埋深的增加，剪胀对地表变形的影响逐渐减小。

基于两种工况下的最大地表沉降的实测值，采用式(8)进行反算，求取了两种工况下修正系数β的取值范围，结果见表3。由表3可以得出，随着隧道埋深的增加，修正系数β的取值范围逐渐减小，也进一步验证了隧道深埋增加的情况下，土体剪胀对地表变形影响较小这一结论。且修正系数β的取值均在0～0.5，所得规律与剪胀系数之间具有良好的一致性。

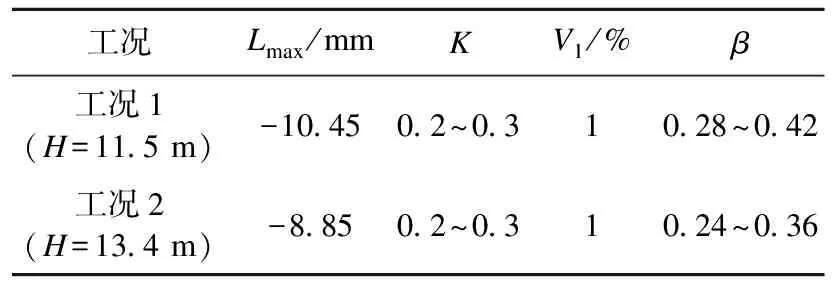
表3 两种工况下修正系数β的取值范围Table 3 The range of values of the correction factor β for the two operating conditions

5 结 论

(1)剪胀角对隧道轴线正上方最大地表沉降有显著影响，最大地表沉降随着剪胀系数的增加而减小。

(2)采用相关联流动准则和非关联流动准则所得到的最大地表沉降的差值随着支护力的增大而增大。

(3)随着隧道埋深比的增加，土体剪胀作用对地表沉降的影响逐渐减小。H/D<2时，随着剪胀系数的增大，塑性体积应变增量变化区段由隧道拱顶转移到拱要处。当H/D≥2时无论采用非关联性流动准则还是关联性流动准则，隧道掘进土体体积应变增量的变化区均集中到了隧道拱腰处，拱顶处并未发生变化。因此，盾构浅埋地段分析地表变形时，应慎重考虑剪胀角的选取。

(4)基于数值模拟、实测数据以及经验公式三者间的对比我们发现，修正系数β与剪胀系数η在预测土体剪胀对地表变形规律方面具有良好的一致性。