平列式公铁两用钢桁梁桥节点动力响应及冲击系数研究

王佐才，董婷婷，孙晓彤,2

(1.合肥工业大学土木与水利工程学院，安徽 合肥 230009；2.安徽省基础设施安全检测与监测工程实验室，安徽 合肥 230009；3.土木工程防灾减灾安徽省工程技术研究中心，安徽 合肥 230009)

桥梁在交通运输中发挥着重要作用，钢桁梁公铁两用桥建筑高度小、空间利用率高，能满足日渐增长的交通量需要，同时其自重轻、刚度大的优势使结构具备较强的承载能力[1]。随着我国交通运输向重载化、高速化发展，公铁两用桥在我国的桥梁建设中获得了广阔的应用。

国内对桥梁结构车桥耦合振动分析已相对较为成熟，在车桥耦合振动分析中，一般采用简化的弹簧质量模型、多轴二系悬挂平面或者空间模型来建立车辆模型[2-3]，然后再开展移动车辆荷载作用下的车桥耦合振动研究[4-5]。由于桥梁实际运营所承受的是车流荷载，近年来学者开始关注车流荷载对结构的动力响应[6-9]。根据桥梁车桥耦合效应可以进一步开展桥梁动力冲击系数研究，进而探明移动车辆荷载作用下的动力放大效应[10]。桥梁的整体冲击系数一般以结构整体动力响应为依据。然而近年来研究表明，桥梁整体冲击系数与局部冲击系数计算结果存在差异[11]，一些构件的冲击效应和桥梁局部动力响应关联性更强。因此，通过分析桥梁不同位置的局部冲击系数不均匀性以及影响冲击系数的因素[12-14]，可以获悉桥梁受动力荷载作用影响显著的关键部位。

公铁两用钢桁梁桥的节点连接主桁和桥面板，受力复杂，是结构的薄弱构件[15]，目前针对钢桁梁节点冲击效应，考虑列车和汽车同时作用下的动力冲击效应研究相对较少[16]。基于此，笔者以某平列式公铁两用钢桁梁桥为例，依托多体动力学建立桥梁柔性体子系统和列车、汽车多刚体子系统模型，采用Hertz接触模型模拟轮轨相对变形关系，通过Craig-Bampton法获得桥梁结构的动力响应。在此基础上，研究列车作用和汽车作用下的钢桁梁节点的应力冲击系数，探讨冲击系数随车速、载重、不平整度变化的规律，并将以数值方法得到的冲击系数值与参照不同规范计算的值进行比较。研究结果表明，相较仅列车作用，考虑列车和汽车同时作用时节点应力冲击系数计算值增大了10.31%，节点应力冲击系数随车速、载重增加不呈单一变化趋势，而随平整度变差迅速增大。研究结果对动载作用下的平列式公铁两用钢桁梁桥动力响应特性和冲击系数选取具有较强的参考价值。

1 基于Craig-Bampton法的车桥耦合振动方程求解

(1)

式中：Kα、Mα、Kβ、Mβ分别表示子系统α、子系统β的刚度、质量矩阵。

首先通过式(2)求解固定界面低阶主模态：

(2)

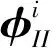
由式(3)可得子系统全部界面坐标的约束模态：

(3)

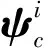
(4)

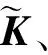
(5)

(6)

(7)

(8)

式中：T表示考虑几何协调条件的坐标变换矩阵。

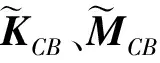
(9)

(10)

式中：ωCB表示系统整体广义坐标对应的圆频率。

笔者依据上述方法，建立桥梁柔性体子系统和车辆多刚体子系统，桥梁子系统中考虑轨道，采用Hertz接触模型模拟轮轨相对变形关系。组合多个子系统及其模态信息，形成车桥整体系统并求解车桥耦合振动方程。

(11)

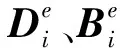
2 工程算例

2.1 工程概况

笔者以某平列式公铁两用钢桁梁桥为算例，桥梁主跨128 m，公铁线路采用非对称平列式布置形式(见图1)，单线铁路与双线公路位于同一水平面，同时铁路线路偏离纵向中心线，靠近桥面一侧布置。桥梁主桁桁高16 m，上、下弦杆分别为1.45 m、1.6 m高的箱形截面，桥面系为正交异性板，板厚16 mm，设U肋和板肋加劲，铁路轨道下方设有两道倒T肋纵梁；桥面系每间距3 200 mm设一道横隔板。建立的有限元模型如图2所示。

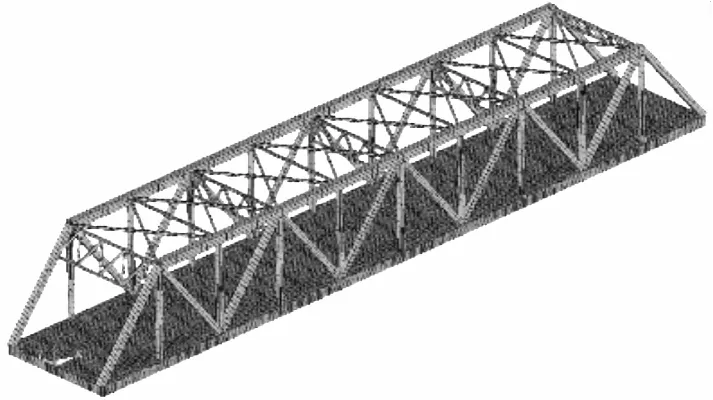
图2 钢桁梁桥有限元模型Fig.2 The finite element model of the steel truss bridge

其中桥面板、横隔板和加劲肋均用壳单元模拟，上、下弦杆、腹杆及横纵联结系用梁单元模拟，腹杆与桥面板间设刚性连接，所采用钢材的弹性模量、泊松比分别为2.06×1011Pa和0.3。通过有限元分析获取桥梁模态信息，并作为柔性体子系统导入整体车桥系统，桥梁前三阶模态频率及振型见表1。

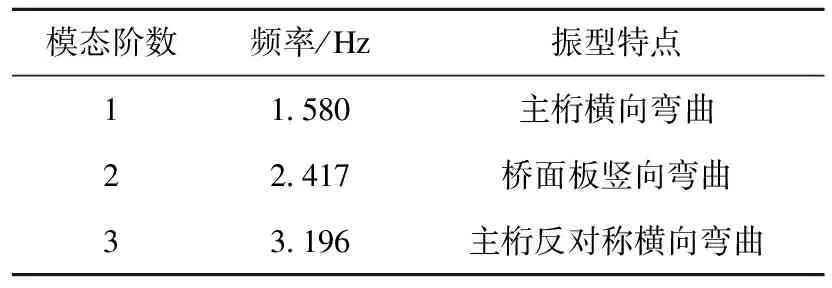
表1 桥梁动力特性Table 1 Dynamic characteristics of the steel truss bridge

2.2 车辆多刚体模型

车辆由多个刚体组成，每个刚体有绕x轴、y轴、z轴3个平动自由度和3个转动自由度。选取符合实际的列车及汽车二系悬挂系统刚度、阻尼参数，通过一系列不同自由度铰和力元连接各个刚体，建立车辆多刚体模型。获取多刚体模态信息，作为子系统导入整体车桥系统。

为模拟桥梁运营期内交通状况，以同路线路段动态称重系统采集的公路交通流数据为依据，统计分析一定时间内过往车辆的车型、车速、车重及车间距等参数分布特征，采用Monte-Carlo算法生成桥梁随机车流荷载模型，作为本算例的汽车荷载模型。同时选取符合实际运营状态的列车编组建立列车模型。建立列车和不同类型汽车的多刚体模型如图3所示。

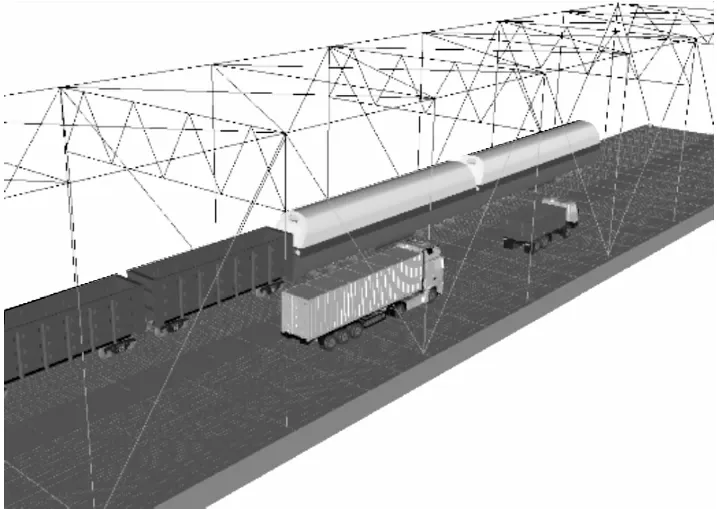
图3 车辆多刚体模型Fig.3 The multi-body models of train and vehicle

3 节点动力响应分析

通过车桥耦合振动计算，车辆过桥引起钢桁梁跨中节点动力响应较大，图1所示跨中腹杆与桥面板交接处两侧节点1和节点2因列车上桥引起的动挠度差值为2.45 mm，约占单侧节点动挠度值的11.84%，铁路侧节点的下挠程度明显高于公路侧，本节重点研究铁路侧节点1的动力响应，加载工况：工况一为仅汽车作用；工况二为仅列车作用；工况三为列车和汽车同时作用。

图4为列车以80 km/h速度过桥，钢桁梁跨中节点1的加速度响应时程。由图可知，车辆激励下节点1竖向加速度值明显高于横向，结构竖向平稳性相对于横向较差。汽车引起节点1的加速度响应值较小，列车与汽车同时作用下节点竖向加速度响应略高于仅列车作用，其最大值增大约3.47%。

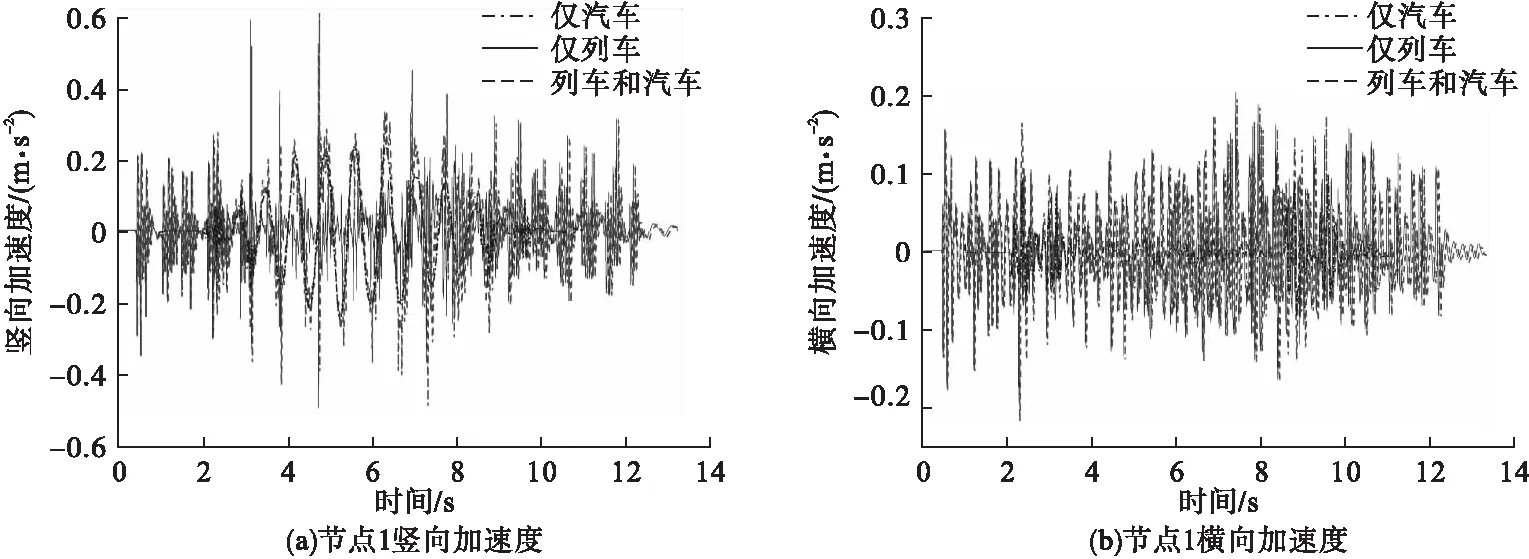
图4 跨中节点1加速度响应时程Fig.4 The acceleration of the joint 1 at mid-span

图5为节点1位移响应时程。由图可知，车辆过桥引起的节点竖向位移响应远大于横向，列车与汽车同时作用下，节点1竖向位移绝对值峰值达到33.79 mm，远高于横向1.35 mm；同时，汽车引起的节点竖向位移与列车相比较小，横向位移的方向与列车作用相反。相对仅列车作用，列车与汽车共同作用时节点1横向位移响应有略微减小，而竖向位移响应增大显著，其最大值增加了27.61%。

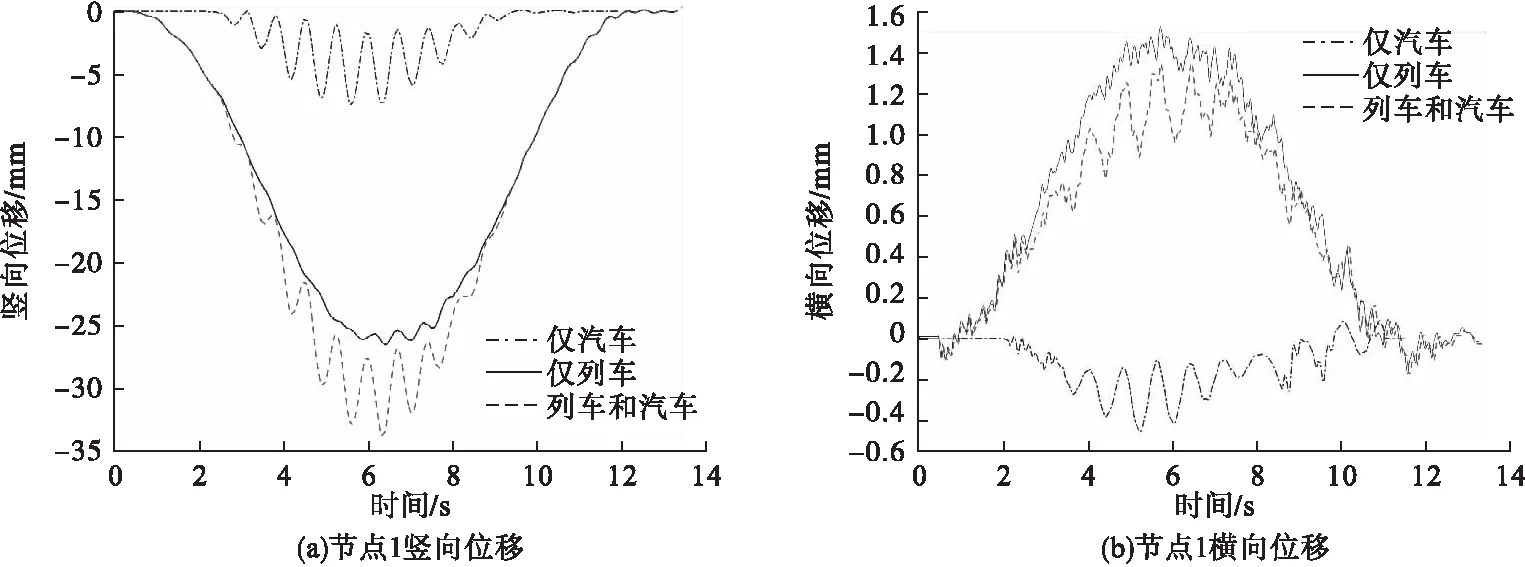
图5 跨中节点1位移响应时程Fig.5 The displacement of the joint 1 at mid-span

图6为节点1最大主应力时程。由图可知，汽车荷载引起的应力水平较小，相对于仅列车作用，列车与汽车同时作用对应力增大效果显著，主应力峰值由仅列车作用下17.40 MPa增至22.89 MPa，提高了31.54%。此外，列车与汽车同时作用时应力时程振幅明显增大，可见汽车的加载一定程度上加剧了对节点的冲击作用。

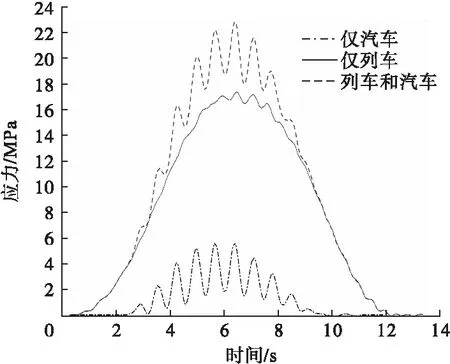
图6 跨中节点1应力响应时程Fig.6 The stress of the joint 1 at mid-span

4 冲击系数

车桥耦合分析中以冲击系数作为衡量车桥动力效应放大程度，冲击系数(1+μ)可表示为

(12)

式中：Rdyn和Rsta分别表示移动车辆荷载作用下桥梁测点位置的最大动、静响应。

4.1 冲击系数规范取值

《铁路桥涵设计规范》(TB 10002—2017)[17]中取冲击系数(1+μ)为跨度L的函数，对于简支钢桥跨结构：

(13)

《公路桥涵设计通用规范》(JTG D60—2015)[18]中取μ为桥梁基频f的函数：

(14)

参照上述规范，按结构基频计算得到该钢桁梁公铁两用桥节点的冲击系数值为1.065，按桥梁跨度L计算得到的值为1.167，可以看出，以跨度计算的冲击系数值更保守。当列车以设计时速80 km/h行驶，采用应力指标，按式(12)计算仅列车作用下节点1的应力冲击系数为1.018，列车和汽车共同作用时应力冲击系数为1.123，计算结果增大了10.31%。

4.2 节点冲击系数随列车车速变化规律

由于平列式钢桁梁桥存在横向受力不均匀，因此本节研究钢桁梁跨中截面，列车侧节点1和公路侧节点2的应力冲击系数。以采用Monte-Carlo算法生成的桥梁随机车流荷载模型作为所研究桥梁的汽车荷载，计算得到节点1和节点2的动力冲击系数分别为1.26和1.34，显然靠近公路侧的节点2受汽车作用影响更大。由于计算仅汽车作用下的冲击系数综合考虑了车速、车重和车距的影响，计算结果为常数，后续冲击系数的影响因素研究就不再单独考虑仅汽车作用这一工况。

为探讨列车行驶速度对冲击系数的影响，以10 km/h为间隔，取50～100 km/h六组车速，不同工况下各节点的冲击系数值如图7所示。

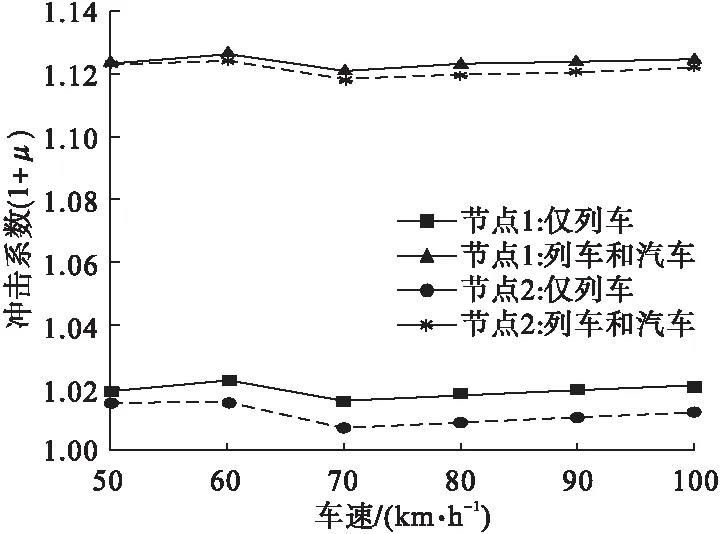
图7 列车不同车速作用下计算的冲击系数Fig.7 The impact factors with various train speeds

由图7可知，冲击系数值随车速增加变化幅度较小，且不呈单一变化趋势。由于货运列车重量大导致结构具有较大静力响应，仅列车作用计算的冲击系数要低于铁路规范建议以L计算的值，列车与汽车同时作用时节点冲击系数值明显提高，冲击系数均在车速为60 km/h时达到峰值，节点在该车速下，受到的冲击效应更明显。仅列车作用或者列车和汽车共同作用时，列车行驶侧的节点1的冲击系数值都高于汽车行驶侧的节2，列车行驶侧的节点动力冲击效应比汽车行驶侧的节点动力冲击效应更为显著。

4.3 节点冲击系数随列车载重变化规律

本节考虑两节货运机车+8节敞车的列车编组形式，设置车厢载重以10 t为间隔，从50～90 t递增，五组载重对应各节点的冲击系数如图8所示。

由图8可知，仅列车作用工况对应的冲击系数值整体较小，随着载重增加变化的范围不大；列车和汽车共同作用时，节点冲击系数值呈现随载重增加而减小的规律。仅列车作用时，节点1、节点2冲击系数的差值相对明显，这表明列车靠近单侧行驶对节点1冲击作用更大；而列车与汽车共同作用时，两节点的冲击系数比较接近。

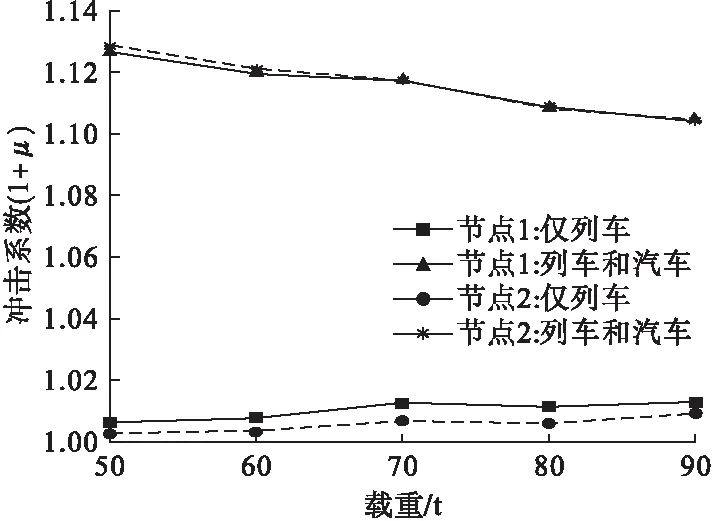
图8 不同列车载重作用下计算的冲击系数Fig.8 The impact factors with various train weights

4.4 节点冲击系数随不平整度变化规律

本节采用美国ARR标准轨道谱一至六级的轨道不平顺度，其中一级代表不平顺度最差，六级表示不平顺度最好。参照《车辆振动输入路面平度表示方法》(GB/T 7031—1986)建议的功率谱密度函数，选取合适平整度系数，生成公路不平整度“非常好”、“好”、“一般”、“差”、“非常差”五个等级。

组合公路路面不平整度与铁路轨道不平顺度，将桥面总路况划为五个等级，组合形式见表2。

表2 路况组合形式Table 2 Unevenness combination of the railway and the highway

不同路况对应的各节点冲击系数值如图9所示。由图可知，两工况下节点冲击系数值均随着路面平整度变差迅速增大，当路况等级为“非常差”时，列车与汽车共同作用工况对应的冲击系数值甚至超过了《铁路桥涵设计规范》(TB 10002—2017)建议的取值。列车和汽车共同作用时，计算的节点1和节点2的冲击系数值均远高于仅列车作用的冲击系数值。此外，仅列车作用工况对应的冲击系数计算结果与按式(14)用基频的计算值更接近，而列车和汽车共同作用工况对应的冲击系数计算结果与按式(13)用跨度的计算值更接近。

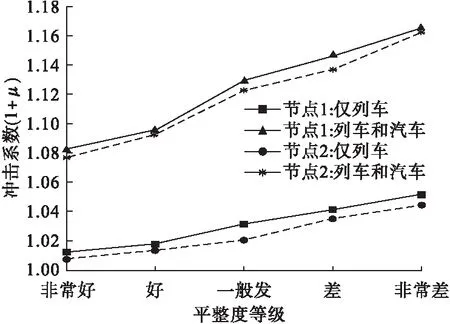
图9 不同路况下计算的冲击系数Fig.9 The impact factors with various unevenness levels

5 结 论

(1)仅汽车作用下钢桁梁节点动力响应相对较小，列车和汽车同时作用时，钢桁梁节点竖向加速度、竖向位移和应力响应最大值较仅列车作用分别增大了3.47%、27.61%和31.54%。

(2)相较仅列车作用，列车和汽车同时作用时应力冲击系数计算结果显著增大，增大幅度为10.31%。

(3)钢桁梁节点应力冲击系数值随列车车速或载重增加变化幅值较小，而随路况变差迅速增大。

(4)仅列车作用时跨中列车行驶侧节点1所受的冲击效应更大，列车和汽车同时作用时两节点所受的冲击效应相对更为均衡。