变截面UHPC-波形钢腹板组合箱梁扭转效应试验研究

郭绍昌 李立峰，2 冯威 杨深

1.湖南大学土木工程学院，长沙 410082；2.风工程与桥梁工程湖南省重点实验室，长沙 410082；3.西安公路研究院有限公司，西安 710065

我国桥梁以混凝土桥梁为主，为响应国家环保、节能、可持续发展的理念，钢-混组合结构、高性能材料等［1］开始在国内大量使用。其中，波形钢腹板PC（Prestressed Concrete）组合梁桥作为一种受力明确、节约材料、施工方便且能避免腹板开裂的钢-混组合结构，已开始广泛应用［2-3］。截至2021年，国内已建及在建的波形钢腹板桥梁约有150座。然而传统预应力混凝土波形钢腹板组合桥梁中的普通混凝土顶底板抗拉强度较低，在结构受拉区易开裂，可能会直接影响结构防水性、耐久性、承载力等性能。超高性能混凝土（Ultra-High Performance Concrete，UHPC）是近年来逐渐被广泛应用的工程材料，具有高强度、高韧性、超强耐久性等优点［4］，用UHPC代替传统波形钢腹板组合桥梁中的NC（Normal Concrete）顶底板［5］，可减轻结构自重，充分发挥新型材料优越力学性能，使结构更加符合绿色、轻型、合理受力的设计理念。由于UHPC具有超高的强度，在满足承载力的要求下，UHPC结构的尺寸远小于普通混凝土结构。因此采用UHPC材料后的波形钢腹板桥梁，箱梁顶底板尺寸将会减小［6］，势必削弱截面抗扭刚度，导致结构扭转性能降低。出于结构安全性、适用性考虑，该新型结构的扭转问题必须重点关注。

国内外学者对于波形钢腹板PC组合梁桥扭转性能已有了较多探索与研究。文献［7-8］中最先应用软化桁架模型理论，提出了波形钢腹板PC组合箱梁抗扭承载力的计算公式；文献［9］通过有限元模型对Mo的理论进行了验证，结果吻合良好；文献［10］对Mo提出的软化桁架理论改进后，能较好预测加载全过程的扭矩-扭率曲线；文献［11］推导了该类桥梁的扭转微分方程，并结合初参数法得到了较为准确的约束扭转应力；文献［12］对波形钢腹板组合箱梁的刚性扭转和畸变性能进行了有限元模拟、理论推导和试验研究；文献［13-17］对波形钢腹板PC组合箱梁扭转性能进行了理论、试验及有限元分析。

基于上述研究及应用现状，本文对变截面UHPC-波形钢腹板组合箱梁扭转性能进行研究。参考巴江河大桥结构尺寸设计制作大比例组合箱梁，在简支、悬臂条件下，对正载、偏载工况时结构的变形、应力进行测试研究，并与ABAQUS计算结果进行对比，分析该新型结构扭转效应并提出在偏载作用下的扭转偏载系数，以期对日后的应用提供参考。

1 试验方案设计

1.1 模型设计

结合调研数据，试验梁采用与巴江河大桥相同的顶底板宽度比例，梁高按比例缩小并微调，按二次抛物线变化。为了便于制作，顶底板及波形钢腹板均采用等厚度的形式。过渡段内箱梁顶底板均采用UHPC，厚度保持50 mm不变。试验梁构造见图1。

波形钢腹板所用材料为Q345C钢，波长12 cm，波高3 cm，厚3 mm，水平折叠角度45°。钢腹板上下端分别设置厚4 mm、宽80 mm的盖板，通过抗剪栓钉将波形钢腹板和顶底板进行刚性连接，波形钢腹板规格及钢-混连接方式参见图1（d）。此外，模型梁共布置8束规格为ϕs15.2 mm的1 860级体外预应力钢绞线，张拉控制应力为1 339 MPa。

图1 试验梁构造（单位：mm）

1.2 试件加工

按波形钢腹板制作、顶底板模板安装、浇筑顶底板UHPC、蒸养、模型就位、预应力张拉的顺序进行试件加工。具体步骤为：在冷轧弯曲后的波形钢腹板上下端分别焊上钢盖板，盖板上均匀布置抗剪栓钉作为剪力连接件；依次安装底板模板、端模板，绑扎底板及端部位置普通钢筋，设置预应力孔道，浇筑底板UHPC及端部C50混凝土；以波形钢腹板为支撑，安装顶板模板，绑扎钢筋后进行浇筑，待构件终凝后拆模，在试验室内采用高温（90±2）℃蒸汽养护72 h后自然养护28 d，单端张拉预应力。浇筑模型梁的同时制作相应的立方体、棱柱体等材性试验所需试块。制作完成的试验梁见图2。通过后续试验测得UHPC弹性模量为51.25 GPa，抗压强度为156 MPa，C50混凝土抗压强度为54.2 MPa。

图2 试验梁

1.3 试验工况及加载方式

根据组合箱梁在施工、使用中可能出现的受力状况，设计了4个试验加载工况：悬臂正载、悬臂偏载、简支正载、简支偏载。偏载工况时施加集中力P，在正载工况时将其均分并对称施加于结构横截面。其中，悬臂工况的纵向加载位置为悬臂梁端部（图1中的A截面处）；简支工况在简支梁跨中位置进行加载，为保护应变计，在纵向距梁端2.234 m处加载。各试验工况对应的纵向、横向加载位置如图3所示。

图3 试验梁各工况加载位置

采用反力架和千斤顶施加荷载。在悬臂偏载工况中，为保证受扭时悬臂边界的可靠性，预先将中支座处的两个千斤顶加载至300 kN，起到预压的作用。在模型梁根部用精轧螺纹钢筋将其锚固于地槽以确保悬臂扭转试验的顺利进行。

1.4 测量方案

使用标定后的力传感器采集荷载。共选取模型梁上4个截面，分别在顶板左右两侧放置百分表，侧向设置1个千分表用以检测箱梁变形情况，在支座及固定端底部左右两侧分别布置百分表，顶部设置1个侧向千分表测量试验过程中的支座变形，百分表编号为L1—L14，千分表编号为L15—L20，见图4（a）；沿箱梁纵向共选取了9个截面测量顶底板的应变，每个截面分别布置9个顶板应变片和5个底板应变片，见图4（b）。

图4 百分表、应变计布置（单位：mm）

2 有限元模型建立

为验证本文模型尺寸的合理性，在尺寸设计阶段建立了ABAQUS有限元模型预先展开计算并合理调节模型梁各参数。采用四节点四面体单元（C3D4）模拟UHPC材料，弹性模量为51.25 GPa；用四节点四边形单元（S4R）模拟波形钢腹板，弹性模量为206 GPa；用两节点线性桁架单元模拟预应力钢束，弹性模量为195 GPa。将UHPC与波形钢腹板接触方式设置为完全弹性连接；混凝土与预应力钢束采用MPC（Multi Point Constraints）多点约束；加载位置设边长为9 cm的正方形加载块与加载点绑定，在加载点施加各工况荷载。对有限元模型进行网格划分，见图5。

图5 试验梁有限元模型

3 试验及有限元结果分析

3.1 简支工况

3.1.1 试件变形

将位移测量的4个截面由端部至根部分别编号为截面Ⅰ—截面Ⅳ，测得简支正载（P=77 kN）、简支偏载（P=57 kN）下的位移。考虑由两端支座变形引起的刚体位移后，得到简支工况试件各截面的变形量，见表1。可知：各截面试验值与有限元计算值误差较小，截面Ⅱ变形量最大，且在施加大小相同的荷载时，偏载工况下荷载作用一侧的变形量比正载工况更大。

表1 简支工况试件各截面变形量 mm

3.1.2 顶底板正应力

简支正载工况下，试验梁顶底板正应力纵向分布见图6。其中，受压为正，受拉为负。可知：①除跨中加载截面底板位置外，试验值与有限元计算值误差均较小；②除了9#截面，其余测量截面顶板均受压，压应力最大值为-4.6 MPa，底板均受拉，拉应力最大值为7.1 MPa，符合简支梁的规律。③应力由离加载点最近的5#截面向两侧递减，且靠近试验梁根部一侧的变化率稍大；④9#截面作为变截面，其左右位置顶底板尺寸差异较大，截面刚度出现突变，导致两侧变形不协调，这可能是该截面出现反向应力的原因之一。

图6 简支正载工况顶底板正应力纵向分布

对于简支偏载工况，从9个截面中选取3个具有代表性的截面（1#、5#、8#）进行分析，顶底板正应力横向分布见图7。图中，受压为正，受拉为负。可知：①5#截面荷载作用一侧应力有明显增大趋势，顶板压应力最大值、最小值分别为5.0、1.4 MPa；底板拉应力最大值、最小值分别为7.4、3.0 MPa。②由跨中至两侧，应力沿横截面的分布规律出现渐变，两侧支承位置附近顶底板正应力的横向分布规律与跨中相反，且底板的应力变化趋势更加明显。

图7 简支偏载工况顶底板正应力横向分布

3.2 悬臂工况

3.2.1 试件变形

测得P=80 kN时截面Ⅰ—截面Ⅳ悬臂正载、悬臂偏载下的位移，考虑由支座变形引起的刚体位移后，得到悬臂工况下试件各截面的变形量，见表2。可知：试验梁在悬臂端部荷载作用下，最大变形量为6.94 mm，并由端部向根部递减，符合悬臂梁受力规律；偏载状态下，离加载位置最近的截面Ⅰ两侧变形量差值最大，其值为2.03 mm，靠近根部的截面Ⅳ顶板两侧变形量差值仅有0.13 mm；相同荷载作用时，偏载工况下的变形量比正载工况增加约30%。

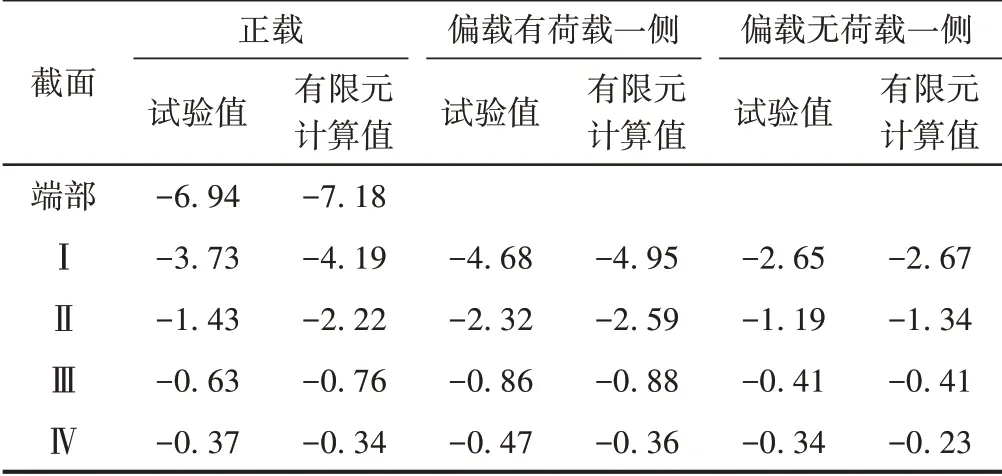
表2 悬臂工况下试件各截面变形量 mm

3.2.2 顶底板正应力

悬臂正载工况下，试验梁顶底板正应力沿梁纵向分布见图8。其中，受拉为正，受压为负。可知，悬臂正载时试验测得的顶底板正应力及其变化规律与有限元计算值接近，顶板纯受拉，底板纯受压，正应力由悬臂端部开始逐渐增大，7#截面顶板、8#截面底板出现峰值后又开始减小，且在悬臂根部附近底板的正应力变化幅度较大。

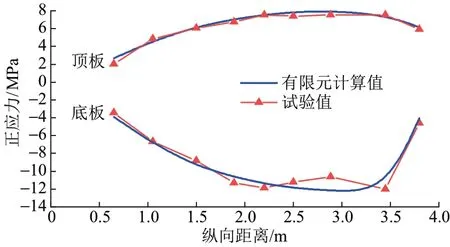
图8 悬臂正载工况顶底板正应力纵向分布

选取1#、5#、8#截面对偏载条件下顶底板正应力进行分析，其横向分布见图9。可知：1#截面应力较小，由于靠近荷载作用位置，导致应力沿横截面变化幅度较大；从悬臂端部至根部，应力呈先增大再减小的变化趋势，且靠近试验梁根部附近的正应力沿横向分布规律与其他位置相反。

图9 悬臂偏载工况顶底板正应力横向分布

3.3 UHPC-波形钢腹板组合箱梁悬臂偏载系数

通过对相同荷载作用下UHPC-波形钢腹板组合箱梁悬臂正载及悬臂偏载时的顶底板正应力进行测试及分析，除去悬臂根部应力复杂的变截面，将每个测试截面偏载时的最大应力与正载时应力的比值定义为偏载应力增大系数η，并得出顶底板偏载系数沿试验梁纵向变化规律，见图10。

图10 悬臂偏载应力增大系数

由图10可知：1#截面上η值达到最大，通过试验得出的顶板ηmax=1.38，底板ηmax=1.20；其他截面处，η值有明显减小趋势，顶板η值的变化范围为0.94～1.11，底板η值的变化范围为0.95～1.16。因此，出于安全考虑，在实际悬臂施工过程中，UHPC-波形钢腹板组合箱梁悬臂偏载应力增大系数的取值不宜低于1.25。

与文献［18］提出的波形钢腹板组合箱梁偏载应力增大系数1.156相比，本文得出的偏载应力增大系数偏高，可见引入了UHPC的新型波形钢腹板结构在一定程度上减小了截面尺寸，导致结构抗扭刚度下降，扭转时的应力增幅比传统波形钢腹板结构有一定提升，实际应用时需要重点关注结构的扭转问题。

4 结论

1）与正载工况相比，偏载工况会使UHPC-波形钢腹板组合箱梁变形量增大约30%，且离荷载作用位置越近，截面两侧横向变形量差值越大。

2）在试验梁根部，截面变化导致中支座两侧截面刚度差值较大，由于变形不协调而出现了应力反向的情况。偏载工况下，应力大小沿横截面出现不均匀分布（底板更明显），且沿梁纵向渐变，荷载作用在支承处的顶底板应力分布规律则呈相反变化趋势。

3）偏载工况下UHPC-波形钢腹板组合箱梁的应力明显增大，应进行深入研究，偏载应力增大系数的取值不宜低于1.25，实际工程中可根据合力偏心距大小适当调整。