客货共线32 m简支梁桥上无缝线路纵向力研究
2022-11-05徐浩刘浩田春香谢铠泽
徐浩 刘浩 田春香 谢铠泽
1.中铁二院工程集团有限责任公司,成都 610031;2.中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081;3.石家庄铁道大学安全工程与应急管理学院,石家庄 050043
桥上无缝线路能改善桥梁与轨道的运营状况,减少养护维修工作量,延长桥梁与轨道结构的使用寿命。相关学者对桥上无缝线路进行了大量研究,形成了系统的桥上无缝线路设计理论。文献[1]介绍了桥上无缝线路的基本原理、设计原则和纵向力的计算方法。文献[2]介绍了高速铁路有砟、无砟轨道简支梁、连续梁等普通桥梁和斜拉桥、拱桥等特殊桥的桥上无缝线路的设计理论。文献[3]验证并介绍了一种桥上无缝线路计算软件的正确性。文献[4]介绍了桥上无缝线路附加力的计算模型。文献[5]研究了桥上无缝线路附加力的计算方法。文献[6]研究了长大简支梁桥上有砟轨道无缝线路的纵向、横垂向变形。
客货共线铁路桥上铺设无缝线路日渐频繁,早期铺设的京九铁路等客货共线铁路也逐步进行了无缝线路改造。另外,2016年客货共线设计活载采用ZKH荷载图式代替中-活载,且客货共线铁路货运特征达到重载铁路标准时应选用ZH荷载图式。因此,有必要研究客货共线铁路桥上梁轨相互作用。文献[7]提出客货共线铁路(40+64+40)m连续梁桥每线墩顶的纵向水平线刚度限值不宜小于1 000 kN∕cm。文献[8]给出了客货共线大跨度简支钢桁梁桥上无缝线路纵向力分布规律。文献[9]研究了客货共线铁路列车荷载图式对桥上无缝线路纵向力的影响。
上述研究均未系统地研究客货共线铁路简支梁桥上梁轨相互作用规律。本文以客货共线32 m跨度简支梁桥为例,基于有限元理论,考虑桥梁与轨道的非线性相互作用,建立客货共线铁路线-桥-墩计算模型,研究客货共线简支梁桥上无缝线路纵向力规律。
1 力学模型及参数
1.1 计算模型
采用有限元软件建立客货共线铁路线-桥-墩计算模型[1-2,10],见图1。客货共线铁路一般采用有砟轨道,鉴于有砟轨道扣件阻力远大于道床阻力,模型中不考虑轨枕结构。用非线性弹簧模拟道床的非线性阻力,桥墩纵向水平线刚度采用线性弹簧模拟。

图1 线-桥-墩一体化计算模型
1.2 计算荷载及参数
选取一客货共线铁路上5×32 m混凝土简支T梁上无缝线路的相关参数进行计算。轨道结构为有砟轨道,采用Ⅲ型混凝土轨枕、CHN60钢轨。桥跨及支座布置见图2。线路纵向阻力采用双线性模型,根据TB 10015—2012《铁路无缝线路设计规范》进行取值,见表1。其中,u为轨枕纵向位移。计算中为消除边界效应,桥梁左右两侧路基长度取120 m[11]。客货共线铁路双线32 m简支T梁的典型横截面见图3。

图2 桥梁布置

表1 铺设Ⅲ型混凝土轨枕时线路纵向阻力

图3 32m简支T梁截面示意(单位:mm)
桥梁温度变化为15℃,且不考虑温度的交替变化。列车荷载图示按ZKH计算,制动时考虑双线制动,制动长度为400 m,轮轨黏着系数取0.164,加载起始位置为0#桥台。桥台及桥墩纵向水平刚度按TB 10015—2012规定的最小限值取值,即桥台的纵向水平线刚度(双线)取3 000 kN∕cm,32 m客货共线铁路桥梁的桥墩纵向水平线刚度(双线)取350 kN∕cm。
2 计算结果及分析
计算荷载作用下客货共线铁路钢轨纵向力,结果见图4。可知:桥梁升温时,客货共线铁路桥上无缝线路伸缩力最大值为108.40 kN,出现在左桥台活动支座附近;挠曲力最大值为49.03 kN(压力),出现在桥梁跨中附近;制动力最大值为387.41 kN,位于左桥台附近。可见,客货共线铁路桥上梁轨相互作用规律与高速铁路一致[2]。

图4 钢轨纵向力变化曲线
下文计算不同桥梁跨数、线路纵向阻力、桥墩纵向水平刚度、列车荷载下的钢轨纵向力,取最大值,研究各参数对桥上无缝线路纵向力的影响。
2.1 桥梁跨数对桥上无缝线路纵向力的影响
仅改变桥梁跨数,分别取2、5、8、10、12、15跨,计算得到不同桥梁跨数下钢轨伸缩力、挠曲力和制动力的变化曲线,见图5。可知,客货共线铁路桥上无缝线路纵向力随桥梁跨数增加而增大,且趋于稳定。这是由于温度作用下简支梁均向活动支座方向伸缩,带动钢轨伸缩,随着桥梁跨数增加,钢轨伸缩力不断积累,但由于线路纵向阻力的传递作用有限,最终趋于稳定。对于挠曲力和制动力,由于列车荷载相同,因此桥梁跨数的影响不大,超过10跨时桥上无缝线路纵向力基本不变。因此,为提高计算效率,客货共线铁路简支梁桥上无缝线路检算取10跨为宜。
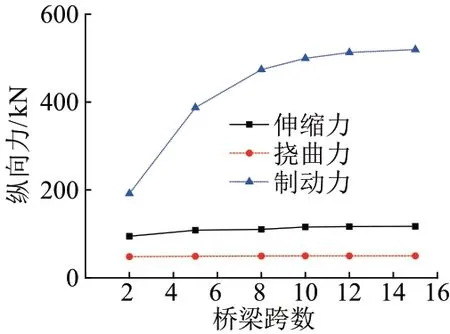
图5 钢轨纵向力随桥梁跨数的变化曲线
2.2 线路纵向阻力对桥上无缝线路纵向力的影响
选取铺设Ⅱ型混凝土轨枕的线路进行对比分析。根据TB 10015—2012,铺设Ⅱ型混凝土轨枕时线路纵向阻力取值见表2。显然,其线路纵向阻力明显小于铺设Ⅲ型混凝土轨枕对应的阻力(参见表1)。取简支梁为10跨,计算不同线路纵向阻力下桥上无缝线路纵向力和梁轨相对位移,结果见表3和图6。可知,随着线路纵向阻力增大,钢轨伸缩力、挠曲力和制动力均有所增大,但制动荷载下梁轨相对位移减小。这是由于线路纵向阻力越大,则梁轨相互作用越强,桥梁变形的约束作用也越强,因此钢轨伸缩力、挠曲力和制动力均随之增大,同时变形约束增强必然导致梁轨相互作用减小。因此,客货共线铁路桥上有砟轨道轨枕选型应综合考虑桥上无缝线路受力、梁轨相对位移等因素。

表2 铺设Ⅱ型混凝土轨枕时线路纵向阻力

表3 不同线路纵向阻力下桥上无缝线路纵向力

图6 不同线路纵向阻力下梁轨相对位移
线路铺设Ⅱ型混凝土轨枕时梁轨相对位移最大值达到4.98 mm,不满足梁轨相对位移4.00 mm限值要求[9],因此需要增大墩台纵向水平刚度(双线),建议不小于500 kN∕cm。
2.3 桥墩纵向水平刚度对桥上无缝线路纵向力的影响
计算不同桥墩纵向水平刚度下客货共线铁路桥上无缝线路纵向力,结果见图7。可知,随着桥墩纵向水平刚度增大,钢轨伸缩力和挠曲力增大,钢轨制动力减小。这是由于桥梁墩台纵向水平刚度越大,桥梁整体位移所受约束越强。对于伸缩工况,梁轨位移相等点越靠近固定支座,钢轨承受的纵向力越大;对于挠曲工况,墩台纵向水平刚度增大,活动支座处桥梁变形增大,导致挠曲力随之增大;对于制动工况,制动荷载一定时,墩台纵向水平刚度增大,桥墩承受的荷载增大,钢轨承受的荷载减小。钢轨制动力减小幅度远高于伸缩力增加幅度,因此增大桥墩纵向水平刚度对钢轨受力有利,但会造成桥墩工程造价增高。

图7 无缝线路纵向力随桥墩纵向水平刚度的变化曲线
铺设Ⅲ型混凝土轨枕时,梁轨相对位移随桥墩纵向水平刚度的变化曲线见图8。可知,随着桥墩纵向水平刚度增大,梁轨相对位移逐渐减小;梁轨相对位移最大值为3.70 mm,小于限值4.00 mm。因此,线路铺设Ⅲ型混凝土轨枕时,客货共线铁路简支桥梁的桥墩纵向水平刚度(双线)不应小于350 kN∕cm。
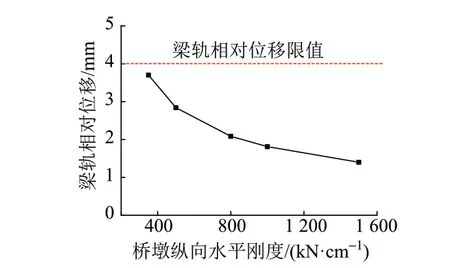
图8 梁轨相对位移随桥墩纵向水平刚度的变化曲线
2.4 列车荷载图式对桥上无缝线路纵向力的影响
列车荷载主要影响挠曲力和制动力,因此主要分析ZKH荷载、ZH荷载(荷载系数为1.1)和中-活载下梁轨相互作用规律。列车荷载根据TB∕T 3466—2016《铁路列车荷载图式》取值。不同列车荷载图式下挠曲力、制动力和梁轨相对位移见表4。
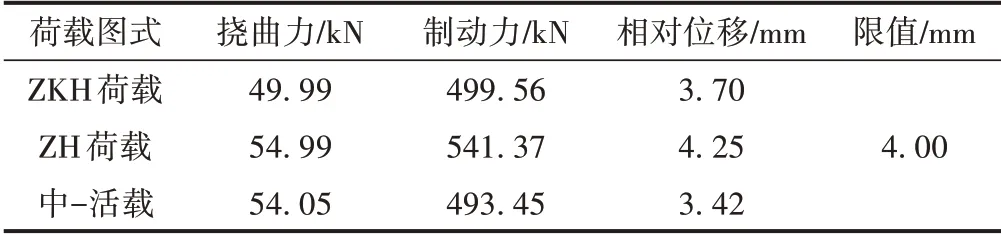
表4 不同荷载图式下无缝线路受力和变形
由表4可知,ZH荷载下钢轨挠曲力、制动力和梁轨相对位移均大于ZKH荷载和中-活载,ZKH荷载与中活载下钢轨挠曲力、制动力和梁轨相对位移相当。可见,当客货共线铁路货运量达到重载铁路等级时,桥上无缝线路纵向力显著增大,且梁轨相对位移达到4.25 mm,这是列车作用荷载显著增大所致。因此,重载铁路桥上无缝线路设计时应增大桥墩纵向水平刚度,以减小钢轨制动力和梁轨相对位移。经计算,列车荷载图示为ZH荷载(荷载系数为1.1)时,为满足梁轨相对位移4.00 mm限值要求,桥墩纵向水平刚度(双线)应达到400 kN∕m,此时梁轨相对位移为3.78 mm。
3 结论
1)客货共线铁路简支梁桥上无缝线路纵向力随桥梁跨数的增加而增大。当简支梁桥达到10跨时,桥上无缝线路纵向力趋于稳定。建议客货共线铁路多跨简支梁桥上无缝线路检算时按10跨简化。
2)钢轨伸缩力、挠曲力和制动力均随线路纵向阻力的增大而增大,但梁轨相对位移减小,因此客货共线铁路桥上有砟轨道轨枕选型应综合考虑桥上无缝线路受力、梁轨相对位移等因素。
3)随着桥墩纵向水平刚度增大,钢轨伸缩力、挠曲力增大,制动力和梁轨相对位移减小。综合考虑梁轨相对位移和桥墩工程造价,建议客货共线铁路简支梁桥的桥墩纵向水平刚度(双线)不小于350 kN∕cm。
4)桥上无缝线路纵向力随列车荷载图式竖向荷载的增大而增大。当客货共线铁路货运量达到重载铁路等级时,需要增大桥墩纵向水平刚度。
