高速铁路道岔区几何不平顺动态管理限值研究

杨爱红 杨飞 孙加林 刁洪宝 徐井芒 李红艳 常文浩

1.中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081；2.中国铁道科学研究院研究生部，北京 100081；3.西南交通大学土木工程学院，成都 610031；4.中国国家铁路集团有限公司铁路基础设施检测中心，北京 100844；5.北京交通大学土木建筑工程学院，北京 100044

道岔结构的几何平顺性一直是道岔设计及养护维修的重点。由于道岔区存在尖轨及心轨断面降低值、轨件密贴间隙等结构不平顺，相较于正线，车辆通过道岔时轮轨接触关系更为复杂。道岔区结构的固有不平顺与轨道随机不平顺产生叠加作用，当叠加效应超出一定范围时，轮对在道岔区的不稳定运动可能会直接影响行车舒适性及安全性。

国内外学者在道岔区动力学行为等方面进行了大量研究，主要是通过仿真建模分析来反映道岔区轮轨接触关系的变化特征。Schupp等［1］研究了在多体动力学仿真中道岔区轮轨多点接触的实现方法。Kassa等［2］研究了关键参数随机输入条件下车辆-道岔系统的动态响应。吴安伟［3］研究了动车组过岔时的动力响应、车轮踏面以及道岔相关参数对车辆振动的影响。朱剑月等［4］分析了道岔尖轨的轨下刚度对轮轨动力特性的影响。全顺喜［5］研究了几何不平顺对道岔区轮轨接触几何关系和车辆-轨道耦合振动特性的影响。司道林等［6］对高速列车通过辙叉区时的动力响应进行了研究，发现设置合理的翼轨抬高值可降低轮轨动力作用。杨东升［7］对高速道岔辙叉结构和平顺性进行了优化。蔡小培等［8］研究得出不同藏尖结构和车轮踏面的轮轨接触不平顺规律。王树国等［9］利用动力学软件建立了高速道岔模型，研究表明尖轨降低值会影响高速道岔转辙器平顺性。

上述研究成果大多集中在道岔区轮轨关系、道岔结构优化设计等方面，较少涉及运营阶段道岔区不平顺的空间几何特征和不平顺管理限值。我国目前对道岔区动态几何状态的评判标准与正线一致，但实际运营过程中道岔区晃车、抖车等现象时有发生，且其成因较为复杂，并非仅受轨道几何状态单因素的影响，尚未明确结构固有不平顺变化、轮轨匹配不良等因素的耦合作用对车辆运行的影响程度。因此，有必要对道岔区轨道不平顺及其管理标准开展研究，深入分析道岔区轨道几何不平顺对车辆动态响应的影响规律，为减少道岔区车辆响应超限提供技术支撑。本文基于动态检测数据，对正线和道岔区的几何不平顺和轮轨力的差异进行分析；基于有限元和多体动力学方法，建立车辆-道岔耦合动力学模型，研究道岔区几何不平顺对车辆动力学性能的影响规律，进而确定道岔区轨道几何不平顺高速控制限值标准。

1 正线与道岔区检测数据统计及对比

1.1 正线与道岔区的轨道几何不平顺差异

基于统计学相关方法，选取京广高速铁路正线及18号道岔区轨检数据，分析其几何不平顺差异。正态性检验［10］结果表明：在0.05的显著水平下，高低、轨向、轨距、水平和三角坑不平顺均不服从正态分布。因此，采用均值及四分位数对其统计特征进行描述，统计结果见表1。在统计数值上存在显著差异的是轨距和轨向。道岔区轨距均值为0.570 mm，比正线的0.148 mm高了285%；道岔区的轨向最小值小于正线，而最大值大于正线，这说明相较于正线，道岔区的轨向分布范围更大。

表1 正线区及道岔区几何不平顺统计数值 mm

轨道质量指数（Track Quality Index，TQI）是7项轨道几何不平顺在200 m区段的标准差之和。正线及道岔区的TQI值统计结果见表2。可知：除高低外，道岔区其他单项几何不平顺的TQI值均显著大于正线，其中轨距差异尤为突出，达0.37 mm；道岔区TQI总值比正线大1.00 mm。

表2 正线及道岔区TQI值 mm

综上，相对于正线，道岔区的轨道几何状态更为恶劣，线路的平顺性相对较差；道岔区采用和正线相同的不平顺管理限值标准是不合理的，不能准确指导道岔区养护维修作业工作，亟待开展道岔区不平顺管理限值的研究。

1.2 正线与道岔区轮轨相互作用差异

选取京哈高速铁路的轮轨力检测数据进行统计分析，得到正线与道岔区轮轨力累计分布上90.0%、95.0%、97.5%、99.5%百分位数处的轮轨垂向力和横向力的统计值，见表3。可知：正线与道岔区轮轨垂向力均在70～83 kN内，道岔区的轮轨垂向力比正线大2～6 kN，轮轨横向力比正线大2～4 kN。

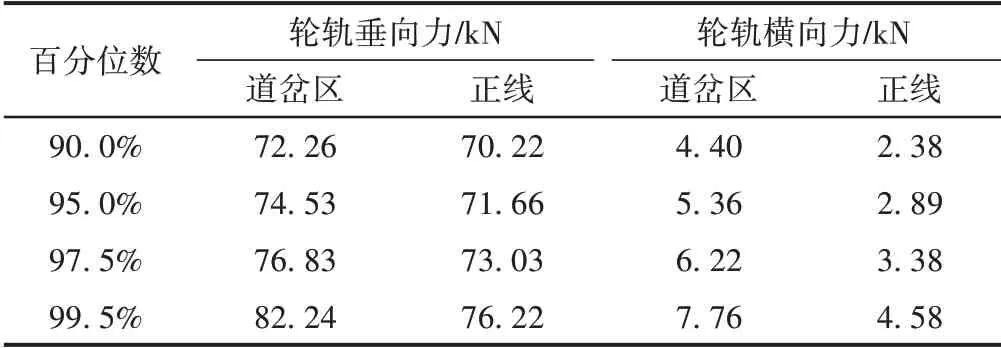
表3 正线与道岔区轮轨垂向力与横向力

2 车辆-道岔刚柔耦合动力学模型

针对我国常用的CRH2C型高速动车组以及18号高速道岔，基于多体动力学软件SIMPACK以及有限元软件ANSYS，建立车辆-道岔刚柔耦合动力学模型。

2.1 车辆模型

在CRH2C型高速动车组多体动力学模型中，车体通过空气弹簧与2个构架进行连接，每个构架通过钢弹簧与4个轮对进行连接；模型中充分考虑了车辆结构的悬挂非线性特性。图1为车辆模型拓扑图。

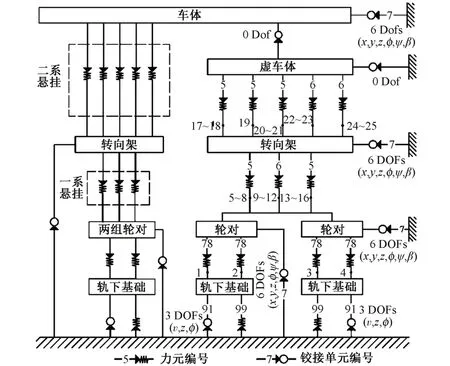
图1 CRH2C型高速动车组建模拓补图

2.2 道岔模型

针对客专07（009）-18号高速道岔，在ANSYS软件中采用beam188单元来建立钢轨模型，考虑道岔区钢轨的柔性变形，且能反映梁模型的纵向变截面特性。选取多个道岔典型截面划分平面单元，将道岔截面的形心作为梁单元的节点，插值形成变截面梁单元。同时，在转辙器和辙叉部分每隔半跨岔枕选取一个钢轨主节点，并在道岔连接部分每隔一跨岔枕选取一个主节点，柔性体变形与车辆子系统通过铰接、约束和力单元进行连接，充分反映变截面梁的高阶弯曲变形特点。道岔直股用钢轨有限元模型见图2。

图2 道岔直股用钢轨有限元模型

模型中扣件垂向刚度取25 kN∕mm；沿道岔纵向模拟了岔枕的变枕距。为减小模型边界效应，在尖轨尖端前和辙叉跟端后设置12跨岔枕长的直线段，模型总长度为73.8 m，自由度数为2 466。

2.3 轮轨接触模型

基于STRIPES条带理论，车轮和道岔钢轨廓形被分割为宽1 mm的系列纵向条带。在每个条带中搜索可能发生接触的椭圆纵轴范围，通过HERTZ和FASTSIM两种算法分别计算轮轨法向和切向接触应力。

2.4 模型验证

为了验证仿真模型的可靠性，计算仿真模型中列车直向通过时安全性指标最大值，并与京沈客运专线（车速v=350 km∕h）18号无砟道岔动力学性能试验结果进行对比，见表4。可知，各项安全性指标仿真计算与试验结果大致相当，且随行车速度、过岔方向变化规律相同；由于道岔制造组装误差、铺设实际状态不同等，二者未完全吻合。应用本仿真模型评估道岔的安全性与动力性能是可信的。

表4 直向过岔时安全性指标的试验与仿真结果对比

3 几何不平顺动态管理限值

3.1 道岔区不平顺工况模拟

基于MATLAB数值计算软件与多体动力学商用软件SIMPACK，参考250 km∕h速度等级（200 km∕h≤v≤250 km∕h）、350 km∕h速度等级（250 km∕h＜v≤350 km∕h）线路轨道几何状态局部峰值动态管理值标准，构造高低、轨距、轨向、水平、三角坑5种类型的谐波不平顺。国内外高速铁路对轨道不平顺以一定弦长下或波长范围内的幅值进行管理。本文参考中国铁道科学研究院集团有限公司在指定既有线铁路轨道不平顺管理值时的方法［11］，采用10 m波长的单一简谐波不平顺，这也与静态检测中10 m弦测波长保持了一致。高低、轨距、轨向、水平谐波波长为10 m；三角坑基长为3 m，在转辙器区前端轨缝外延60 m、岔后轨缝后延60 m，共计189 m范围内。

为模拟车辆真实的过岔状态，得到准确的车辆响应，还需考虑随机不平顺的影响。利用高速铁路无砟轨道不平顺谱生成50个随机样本，分别与上述各单项谐波不平顺相叠加。

基于车辆-道岔系统耦合动力学模型，研究列车直逆向过岔时各单项不平顺幅值变化对运行安全性、平稳性的影响规律，统计50个某单项不平顺样本不同幅值作用下的安全性和平稳性指标的平均值，进而探究道岔区几何不平顺高速分级管理限值控制标准。

3.2 350 km/h速度等级高速道岔动态不平顺管理限值

列车以350 km∕h直逆向过岔时，对高低、轨向、轨距、水平、三角坑5种单项不平顺进行仿真计算，分析其幅值变化对运行安全性、平稳性的影响规律。参照TG∕GW 115—2012《高速铁路无砟轨道线路维修规则（试行）》以及GB∕T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》中有关安全性、平稳性指标分级管理限值的规定，对于单项不平顺，当有一项安全性或平稳性指标达到某级别限值时，提取所对应的该项不平顺幅值作为道岔区几何分级管理限值标准。

对计算结果进行分析，发现除水平不平顺外，高低、轨向、轨距和三角坑不平顺各偏差等级限值均可沿用动态运营管理值标准。

对于水平不平顺，其动力学指标随不平顺幅值的变化曲线见图3。可知，脱轨系数和轮重减载率最大值均随水平不平顺幅值增大而增大；水平不平顺对车体横向振动加速度的影响显著大于垂向振动加速度，其变化幅度达到1.10 m∕s2。水平不平顺幅值为3 mm时，横向加速度最大值达到0.65 m∕s2；幅值为5 mm时，横向加速度最大值为0.92 m∕s2；幅值进一步增大到6 mm，横向加速度最大值为0.95 m∕s2，此时轮重减载率增至1.0。因此，在水平不平顺下，建议偏差等级Ⅰ—Ⅲ级分别取3、5、6 mm，偏差等级Ⅳ级沿用动态运营管理值标准。

图3 动力学指标随水平不平顺幅值的变化曲线

综上，得出350 km∕h速度等级道岔区轨道几何状态局部峰值动态管理建议值，见表5。

表5 350 km·h-1速度等级道岔区轨道几何状态局部峰值动态管理建议值

3.3 250 km/h速度等级高速道岔动态不平顺管理限值

采用与350 km∕h速度等级相同的方法，对高低、轨向、轨距、水平、三角坑5种单项不平顺进行仿真计算，分析其幅值变化对运行安全性、平稳性的影响规律。根据计算结果，高低、轨距和三角坑不平顺各偏差等级限值均可沿用动态运营管理值标准。对于轨向不平顺，当其幅值为6、7、9、10 mm时，车体横向加速度最大值分别达到0.61、1.00、1.68、2.03 m∕s2。因此，在轨向不平顺激励下，建议偏差等级Ⅰ—Ⅳ级分别取5、6、8、9 mm。对于水平不平顺，当其幅值为4、6、10、14 mm时，车体横向加速度最大值分别达到0.71、0.95、1.50、2.09 m∕s2。因此，在轨向不平顺激励下，建议偏差等级Ⅰ—Ⅳ级分别取3、5、9、13 mm。得出250 km∕h速度等级道岔区轨道几何状态局部峰值动态管理建议值，见表6。

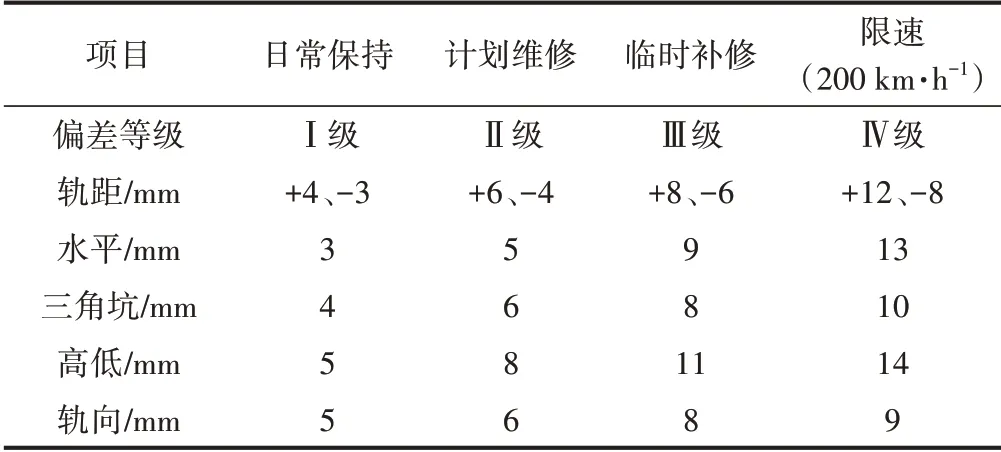
表6 250 km·h-1速度等级道岔区几何状态局部峰值动态管理建议值

4 结论

1）道岔区与正线在轨距、轨向及TQI值方面存在显著差异，道岔区几何状态比正线恶劣。道岔区轨距均值比正线高285%，轨向分布范围比正线大；除高低外，道岔区各单项几何不平顺的TQI值均显著大于正线，其中轨距差异尤为突出，达0.37 mm；道岔区TQI总值比正线大1.00 mm。道岔区与正线在轨道几何管理控制标准方面理应有所差异。

2）对于350 km∕h速度等级18号高速道岔，高低、轨距、轨向、三角坑不平顺可沿用既有350 km∕h速度等级线路轨道几何状态局部峰值动态运营管理值标准；水平标准建议严于正线，偏差等级Ⅰ—Ⅳ级对应限值建议调整为3、5、6、8 mm。

3）对于250 km∕h速度等级18号高速道岔，高低、轨距、扭曲不平顺可沿用既有250 km∕h速度等级线路轨道几何状态局部峰值动态运营管理值标准；轨向标准建议严于正线，偏差等级Ⅰ—Ⅳ级对应限值建议调整为5、6、8、9 mm；水平标准建议严于正线，偏差等级Ⅰ—Ⅳ级对应限值建议调整为3、5、9、13 mm。