基于GABP神经网络的供应链合作伙伴评价方法

李 蕊

（烟台理工学院，山东 烟台 264000）

0 引言

随着全球经济的不断发展，企业之间的竞争逐渐转变为产业供应链间的竞争，供应链的管理成为了竞争的重要环节与手段。我国著名学者马士华，等[1]给出的供应链定义中指出，供应链是围绕核心企业，通过对信息流、物流、资金流的控制从采购原材料开始制成半成品以及最终产品，最后由销售网络把产品送到消费者手中的供应商、制造商、分销商、零售商、直到最终用户连成一个整体的功能网链结构模式。供应链中的核心企业是整个功能网链的中轴，是供应链资金流以及商品流的综合分转核心，以制造企业为例，其供应链中合作伙伴的合理选择是建立高效供应链、赢得最大利益的重要环节，因此，供应链合作伙伴的选择方法成为了该领域研究的重要方向。目前，国内外在供应链合作伙伴评价方法的研究方面有很多成果[2-5]，可归纳为经济分析法、专家评价法、层次分析法（AHP）、模糊综合评价法、灰色关联分析法、数理统计法以及以BP（Back Propagation）神经网络方法等。根据供应链合作伙伴关系的特点，在进行选择过程中需建立科学合理的评价指标体系，这些指标特性的关系往往是非线性的关系，利用专家评价、层次分析法、模糊数学和灰色系统等方法很难反映这种非线性关系，而且这些方法在人的参与过程中，存在主观上的随意性、思维上的不定性，比如，评价指标权重的确定存在较大的主观性，会给评价结果带来较大的影响。神经网络的方法可以很好地解决上述问题，神经网络具有较好的学习能力和泛化能力。神经网络可利用典型的案例集合，通过学习其内部的规则和非线性关系来训练网络内部结构，并可将典型系统中的知识、经验以及对重要性的权衡等信息应用于新的系统，从而得到合理的评价结果，神经网络可以很好地处理这些复杂的非线性问题[6-7]。BP神经网络是一种信息正向传播但是误差逆向传播的神经网络，该网络因其具有较多优点被广泛的应用[8-10]，包括非线性的映射能力、联想记忆能力、自学习能力、自适应能力、泛化能力、容错能力等。然而BP神经网络的使用需要解决几个问题。一般情况下，BP神经网络结构采用三层，即输入层、隐层以及输出层，输入层和输出层节点个数根据任务确定，重要的是隐层节点个数的确定。过多的隐层节点数会使新的输入集难以适应该网络，而过少的隐层节点数会使网络的精度受到影响，因此合理选择隐层节点数是BP神经网络应用必须解决的问题之一。文献[11]中提出设置隐层节点数为ab，其中a、b为输入和输出的节点个数。但是固定的隐层节点数会降低神经网络的自适应性。另一方面，BP神经网络可将网络误差逆向传输从而优化节点间的权重和阈值，直到误差满足要求为止。因此应力求通过最少的训练步数找到最优权重和阈值使网络误差满足要求，从而使BP神经网络具有更好的性能。

本文采用基于遗传算法（GA，Genetic Algorithm）优化的BP神经网络方法进行供应链合作伙伴的评价，其中遗传算法用于寻找BP神经网络的最优权值和阈值。本文，先利用公式ab计算隐层节点数，利用计算得到的值选取一个范围，利用Matlab仿真软件进行仿真论证，找到最优隐层节点数。最后结合供应链合作伙伴评价的实例，验证GABP神经网络方法的有效性。

1 GABP神经网络方法

二十世纪七十年代，美国著名教授霍兰德（J.H.Holland）首次提出遗传算法的思想，将自然界生物遗传与进化思想应用到解决复杂程序中，将“遗传”与“进化”思想应用到人工智能系统中，并且在多个自动化程序设计中得到了较好的应用，遗传算法正在受到人们极大的关注[12]，遗传算法的基本工作流程图如图1所示[13]。

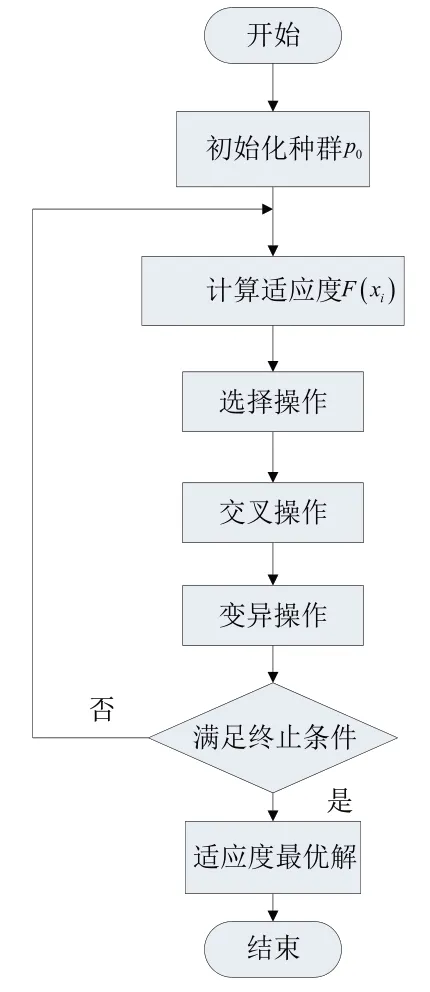
图1 遗传算法流程框图

实际问题中的各个变量映射为一个个染色体，染色体种群经过一系列选择、交叉及变异产生新的个体，构成新的种群，经过自适应度的计算及筛选，得到较优解或最优解[14]。具体的操作如下：

（1）选择。选择操作能够保持染色体的多样性，但是适应度较高的个体也有可能被淘汰，从而使得结果的偏差。

（2）交叉。交叉时两个染色体的部分片段相互交换，从而产生新的染色体。

（3）变异。变异是染色体存在一定的概率变化操作，具体表现为遗传因子的部分片段替换成为与其对立的编码，通过这种方法引入染色体的多样性变化[15]。

BP神经网络的基本结构如图2所示。

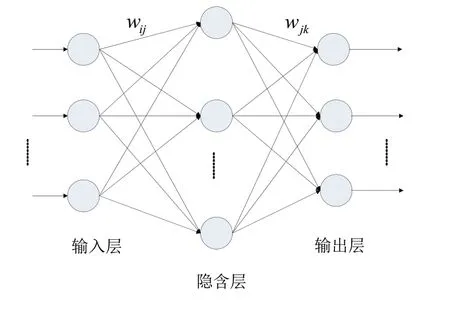
图2 BP神经网络基本结构

利用遗传算法优化的BP神经网络基本工作流程如图3所示。

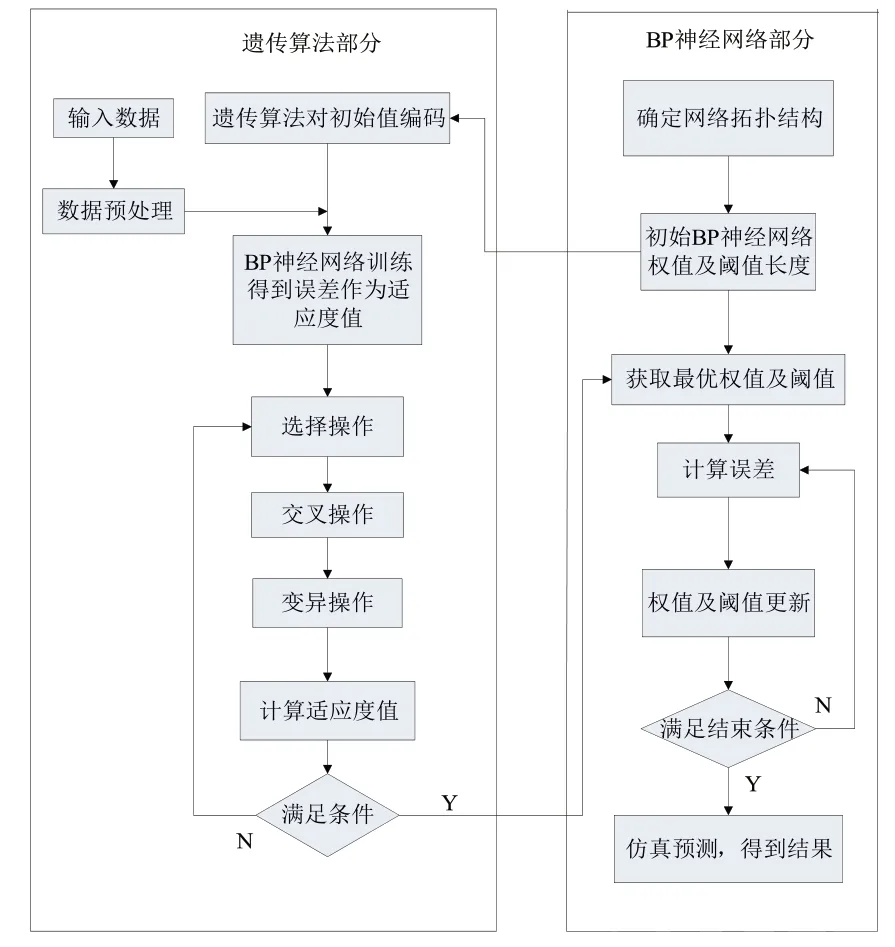
图3 GABP工作流程框图

2 GABP神经网络供应链合作伙伴评价

2.1 评价指标体系

利用GABP神经网络进行供应链合作伙伴的评价，以文献[16]中的实例作为研究对象，即Simplex系统咨询公司为福特汽车全球采购中心寻找机油滤清器供应商的评估结果，对文中13家供应商中前8家的数据进行研究。首先，建立评价的指标体系，为方便比较评价方法的优劣，采用文献[16]中的评价指标体系，见表1，包括四大类评价准则，共27个评价指标。

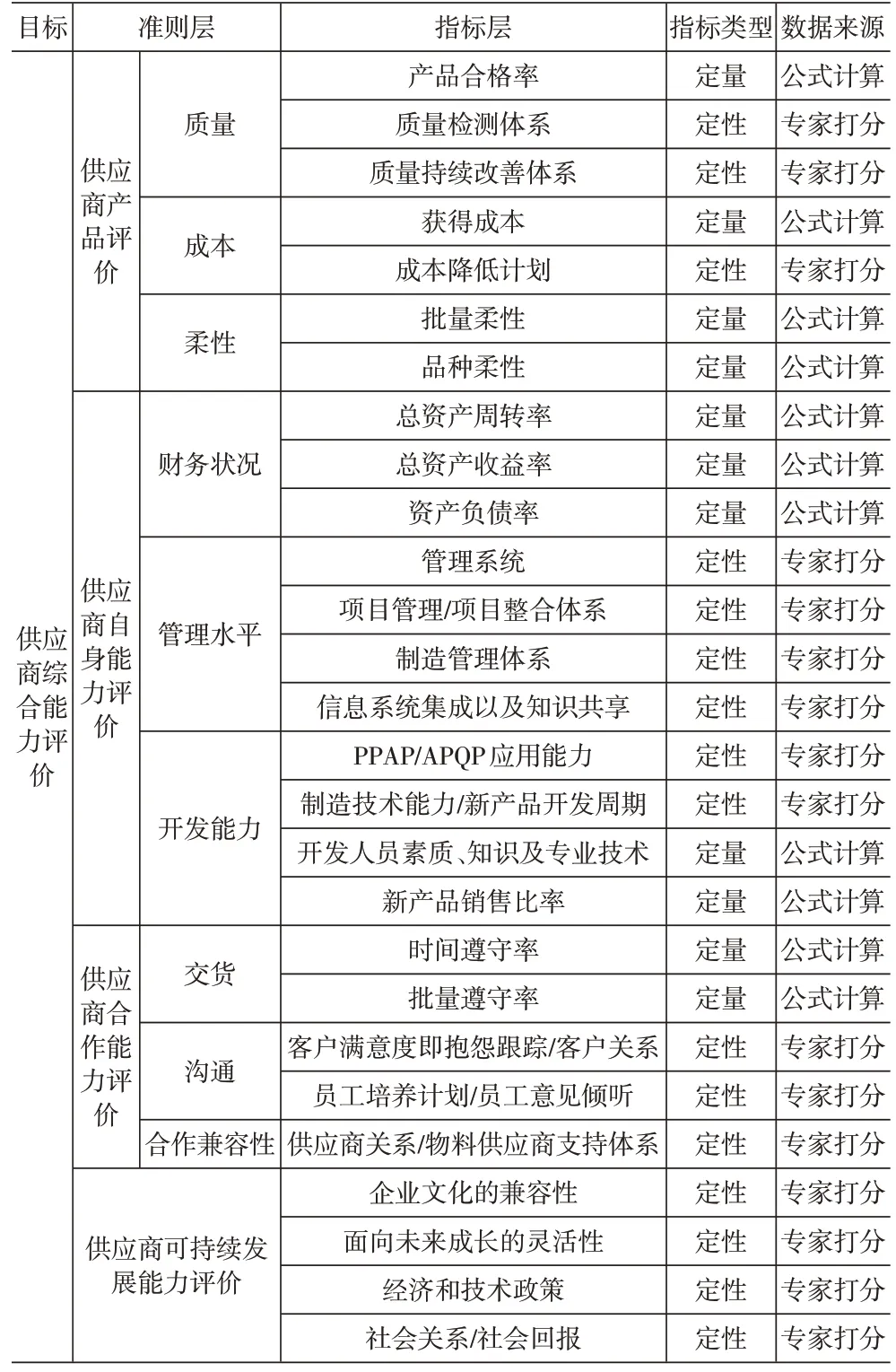
表1 供应商评价指标体系

Simplex系统咨询公司在供应链合作伙伴选择和评价方面有着丰富的成功实践经验，同时具备资深的咨询专家队伍，专家评分具备权威性。借鉴文献[17]的数据，见表2列出的8家候选企业的评分。

表2中A1～A27为27个评价指标，S1-S8为8个候选企业，文献[16]给出了理想目标值，即专家利用加权法得到评价值见表3。将候选企业S1～S5的数据和评价值作为GABP神经网络的训练样本集，将候选企业S6～S7的数据和评价值作为测试样本集。利用网络训练样本集对GABP神经网络进行训练学习，使网络对训练样本集中的规则、知识和认知进行学习，而后将测试样本集中候选企业S6～S7的指标数据作为网络的输入，得到网络评价输出，测试样本集中的评价值进行比较分析，验证GABP神经网络评价方法的有效性。

表3 供应商评价理想目标值

2.2 GABP神经网络评价的Matlab实现

表2中的评价指标数据具有不同的量纲和属性，要使用Matlab软件进行GABP神经网络评价必须将表2中的数据进行归一化处理，根据文献[16]给出的方法，可利用如下的Matlab程序进行归一化：

表2 供应商评价数据

for:i=1:8;

p(i,:)=(p(i,:)-min(p(i,:)))/(max(p(i,:))-min(p(i,:)));

p(i,:);

end;

其中p(i,:)为需要进行归一化的数据，min(p(i,:))、max(p(i,:))分别为其对应的最小值、最大值。归一化后的数据成为[0,1]范围内的数据，见表4。

表4 供应商评价归一化数据

考虑到对候选企业的评价指标有27个，因此GABP神经网络的输入层节点个数设为27个，输出层反映的是评价值，因此输出层节点数设为1个。隐层节点数先利用公式ab进行计算，即为5左右，选择区间设为[5,15]，根据网络训练情况进行调整选定。具体选定过程如下：

P为GABP神经网络的训练样本集的输入向量，选取候选企业S1～S5的评价数据。

t=[0.684,0.554,0.416,0.637,0.667]。t为 训 练样本集的输出向量，为候选企业S1～S5的理想目标值。

tshold=[0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1；0,1]。tshold为输入向量各元素的取值范围。

Y=[5,6,7,8,9,10,11,12,13,14,15]，Y是待选的隐层节点数，通过仿真论证选取最优值。

BP神经网络隐层节点论证程序如下：

for i=1:11

net=newff(tshold,[Y(i),1],{‘tansig’,‘logsig’},‘traingdx’);

net.trainParam.epochs=1 000;

net.trainParam.goal=0.000 001;

net=train(net,p,t);

end

net.trainParam.epochs为仿真步数，net.trainParam.goal为设置的网络目标误差，tansig、logsig分别为输入层到隐层、隐层到输出层的传递函数，traingdx为神经网络的训练函数。若只使用BP神经网络进行训练上述程序即可完成，本文采用遗传算法对BP神经网络的权值和阈值进行寻优。使用遗传算法进行寻优，需要在Matlab软件中调用GAOT工具箱，目标函数定义为gabpEval，即遗传算法的适应度函数，具体程序如下：

net.IW{1,1}=W1；W1为输入层到隐含层的权重矩阵，net.LW{2,1}=W2；W2为隐含层到输出层的权重矩阵，net.b{1}=B1；B1为隐含层的阈值向量，net.b{2}=B2；B2为输出结点的阈值向量。利用遗传算法进行寻优后，再利用BP神经网络进行训练，即执行net=train(net,p,t)，执行结果如图4-图14所示。

图4 隐层节点数为5时训练结果

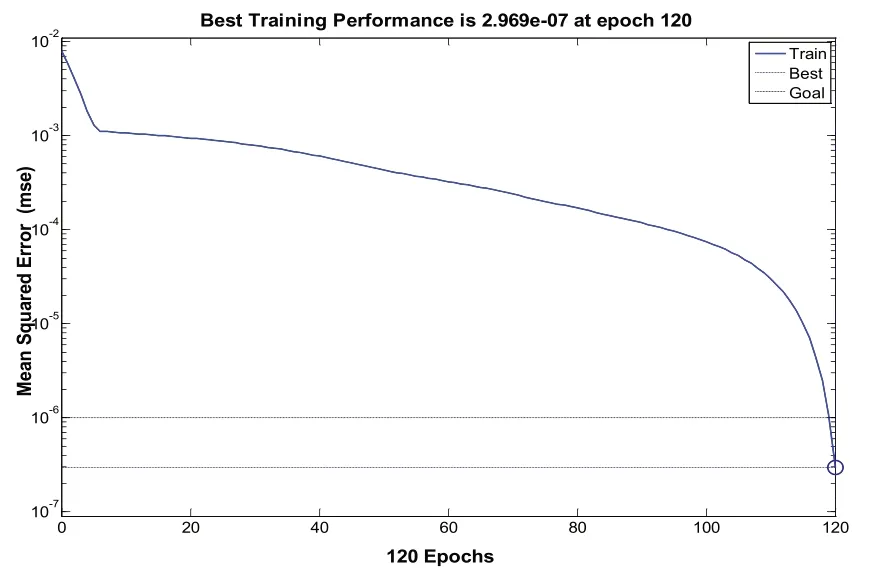
图5 隐层节点数为6时训练结果

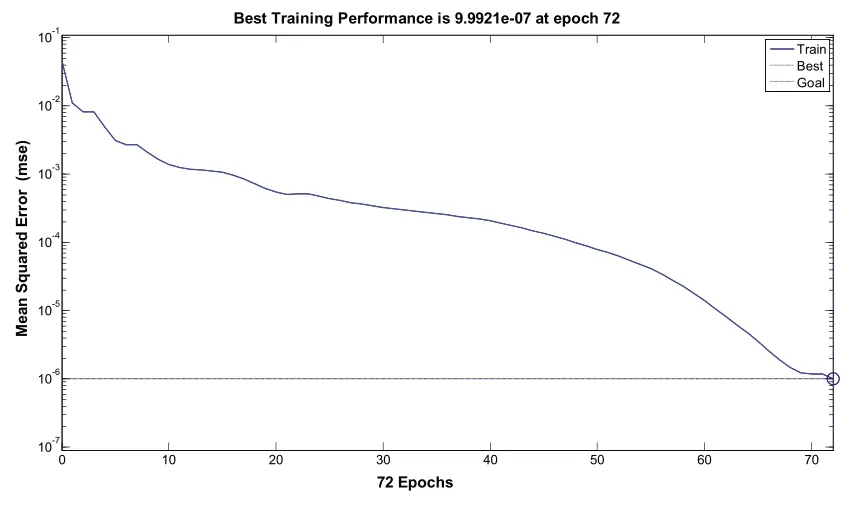
图14 隐层节点数为15时训练结果

通过网络训练结果可以得到训练步数和隐层节点数关系，见表5。

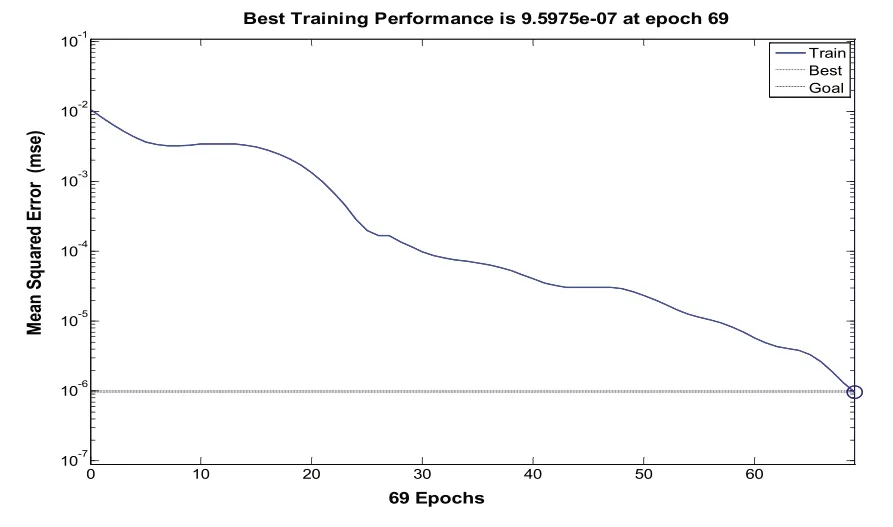
图6 隐层节点数为7时训练结果

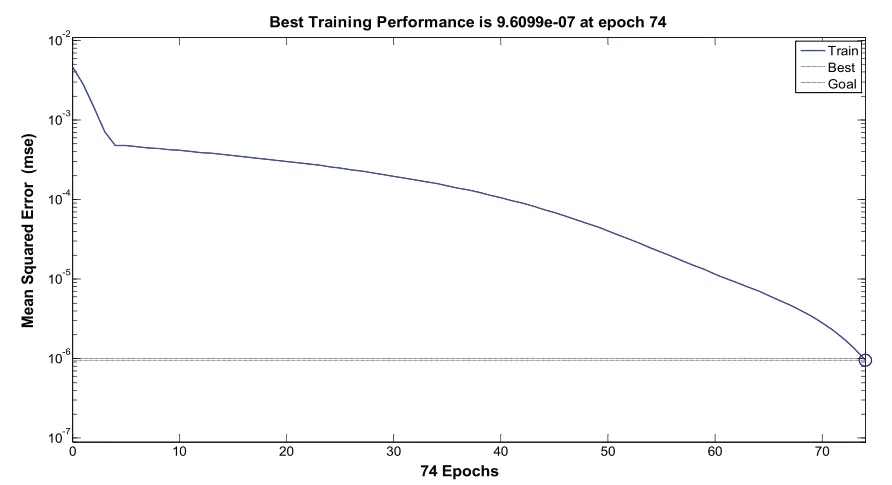
图7 隐层节点数为8时训练结果

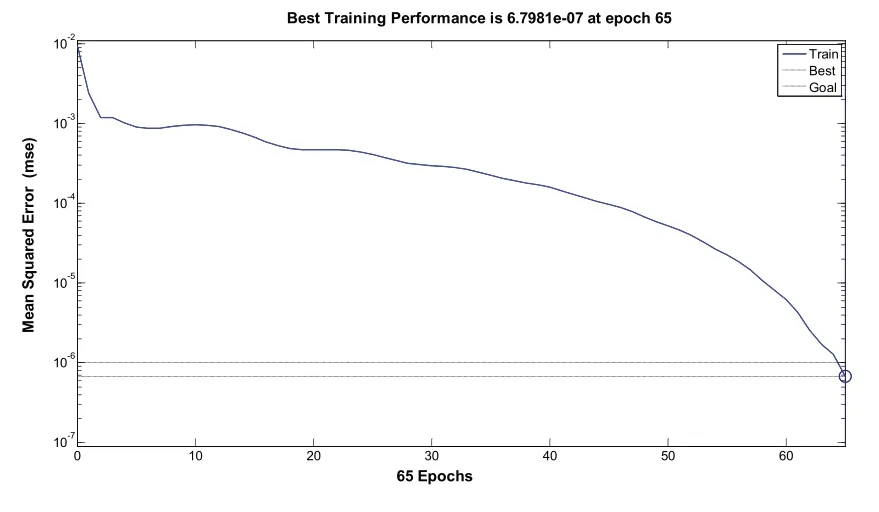
图8 隐层节点数为9时训练结果

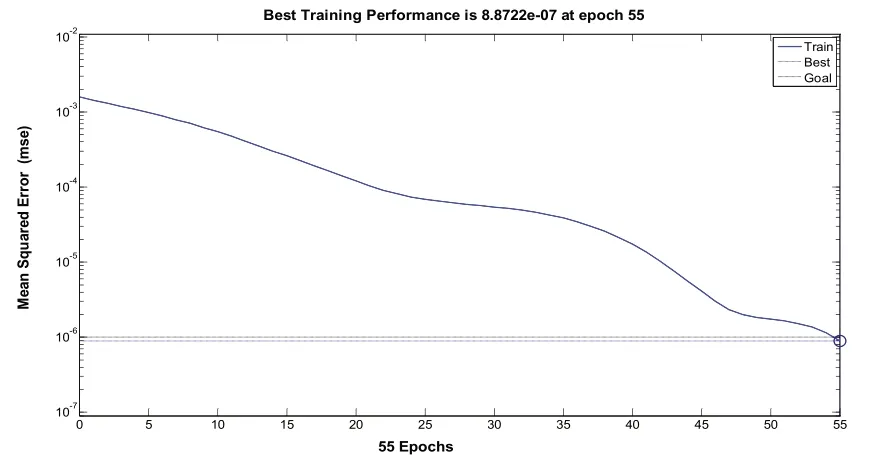
图9 隐层节点数为10时训练结果

通过训练结果图4-14以及表5中的关系，可以很直观地观察到，在隐层节点数为5、6时，网络需要训练100步以上才能达到目标误差要求，在隐层节点数为10时，训练步数为55，然而随着节点数的增加训练步数也随着增加，同时也并不能明显改善网络性能，相反增加了节点数增加了网络负担。因此，隐层节点数选择为10比较合适。

表5 隐层节点数与训练步数关系表

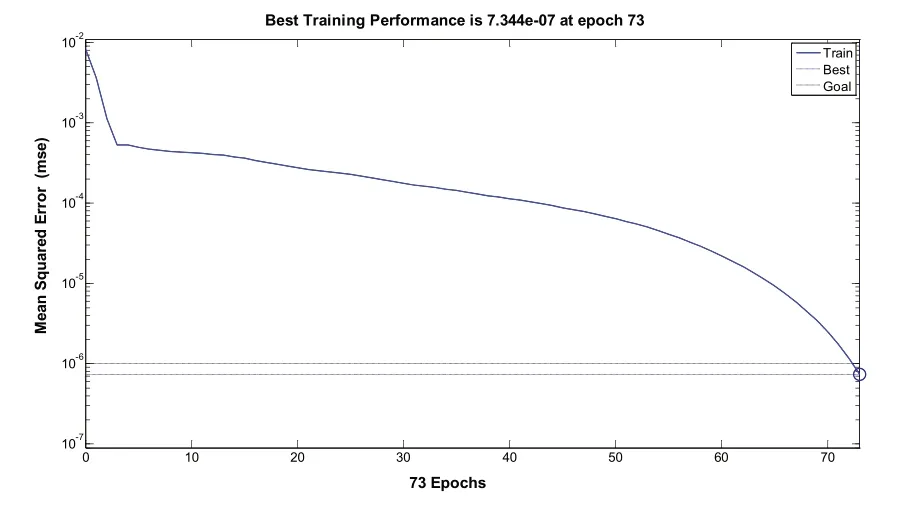
图10 隐层节点数为11时训练结果

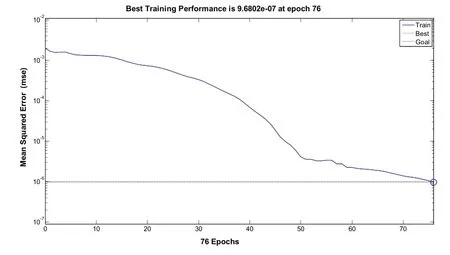
图11 隐层节点数为12时训练结果

图12 隐层节点数为13时训练结果

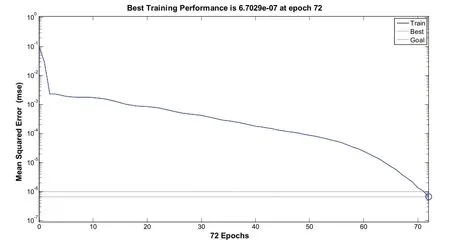
图13 隐层节点数为14时训练结果

隐层节点数设定为10后，完成GABP神经网络的学习训练，即可对测试样本集进行测试。测试样本集的输入量为S6～S8的评价数据，即

测试样本集的目标输出量为t1=[0.375,0.661,0.54]，利用训练完成的GABP网络对测试样本集进行仿真，得到t_test=[0.425 7，0.663 7,0.519 2]，见表6。

表6 GABP评价值与目标值对比表

根据表6中数据的对比可知，利用GABP神经网络的评价值与目标值基本接近，而且排序一致，说明利用GABP神经网络进行供应链合作伙伴的评价方法是有效的。

2.3 对比分析

上文中的结果证明了GABP神经网络对供应链合作伙伴进行评价的方法是有效的。在此基础上，与BP神经网络进行比较分析。

选用相同的训练样本集以及测试样本集，隐层节点数均设为10，图15为BP神经网络训练结果，网络误差达到0.000 001需要经过111步。图16为GABP神经网络训练结果，网络误差达到0.000 001需要经过65步，通过对比可以看出经过遗传算法优化的BP神经网络具有更好的性能。

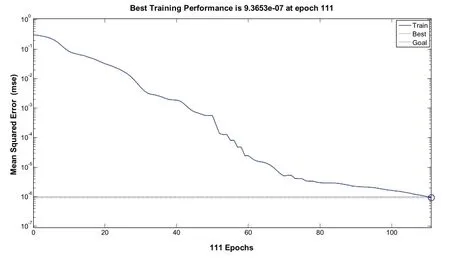
图15 BP神经网络网络训练结果

图16 GABP神经网络训练结果

表7中将BP神经网络评价、GABP神经网络评价与目标值进行比对，可以发现BP神经网络的评价值与目标值相比排序一致，但是评价值与目标值间有着较大的误差，这说明GABP神经网络与BP神经网络在供应链合作伙伴评价方法具有更大的优势。

表7 GABP评价值与BP评价值对比表

3 结语

利用基于遗传算法优化的BP神经网络对供应链合作伙伴进行评价，是一种科学、合理的评价方法。

（1）利用GABP神经网络进行评价，可以尽量减少主观性对评价结果的影响，同时使评价过程更加便捷、准确；

（2）不同于以往的BP神经网络评价方法，利用了遗传算法对BP神经网络的权重和阈值进行寻优，实际上BP神经网络自身的运行机制需要对权重和阈值进行寻优从而降低网络误差，利用遗传算法优化BP神经网络的本质是缩短BP网络对权重和阈值的寻优过程，为网络减小压力，使网络性能更强。与BP神经网络评价方法进行比较可以看出，GABP方法的步数不需100步即可实现0.000 001的网络误差要求，这说明了遗传算法对BP神经网络优化的优势；

（3）在利用GABP神经网络评价过程中，隐层节点数的设置没有比较有绝对优势的确定方法，本文中利用训练样本集对隐层节点数进行训练论证，通过分析最后确定比较合理的隐层节点数，该方法值得推广。