改进共旋坐标法的Timoshenko 梁单元非线性分析

2022-11-05李东升高严培

工程力学 2022年11期

李东升，高严培，郭鑫

(1. 汕头大学土木与环境工程系，广东省结构安全与监测工程技术研究中心，汕头 515063；2. 大连理工大学海岸及近海工程国家重点实验室，大连 116024)

随着科学技术的不断进步，现代工程结构正在向大型化、复杂化和智能化方向发展，如大跨度桥梁、高层建筑和大型风力机等。大型化将导致结构更加趋于柔性，基于传统小变形假设的有限元分析方法有时已不能满足计算需求，因此对结构进行几何非线性分析成为近年研究的热点问题，也是难点问题。关于几何非线性的有限元分析方法，最常用的是以结构变形前为参考建立平衡方程的完全Lagrange 列式法(TL 列式)和以结构变形后为参考建立平衡方程的更新Lagrange 列式法(UL 列式)[1]。其中，TL 列式法在求解大转动问题时，会因参考系的转动引起不可忽略的误差，甚至出现错误的解，而UL 列式法虽然可以求解大转角问题，但非线性应变关系的计算非常复杂，导致计算量也随之偏大[2]。近些年发展起来的共旋坐标法是对上述两种方法的一种改进，它具有建模简单，意义明确，并且能借用现有的有限元理论，求解效率和精度相对较高[3]等特点，成为几何非线性研究的热点。

共旋坐标法的概念最早由WEMPNER 等[4]提出，即通过剔除结构的刚体位移来得到单元节点的真实位移。CRISFIELD[5]使用共旋坐标法求解各种单元的几何非线性，提出了一致的单元平衡方程计算方法。AREIAS 等[6]将共旋坐标法用于分析材料失效破坏及断裂，证明共旋坐标法可以对更复杂的问题进行研究。STÄBLEIN 等[7]基于共旋坐标法，提出了各向异性的Timoshenko 梁单元用于梁单元的几何非线性分析。邓继华等[8]基于共旋坐标法和稳定函数提出了一种几何非线性平面梁单元，杨浩文等[9]将能量守恒和共旋坐标法相结合对二维Timoshenko 梁单元进行动力学分析，杜柯等[10]利用共旋坐标法模拟框架结构的连续倒塌，ZIYUN 等[11]简化并开发了一种新的共旋分析框架，来避免非线性投影矩阵的复杂推导。在共旋坐标法中，材料非线性和结构纯变形等位于局部坐标系内，因此局部坐标系的选取对于精度的计算有显著的影响。通常梁单元局部坐标系的选择有以下几种方法：RANKIN 法[12]、BATTINI法[13]、CRISFIELD 法[14]和HSIAO 法[15]。前三种方法都是通过左右两端总转角值线性插值构造刚体旋转矩阵，当变形较小时，计算结果较为精确；而当变形较大时，会产生较大的虚假应变。对于HSIAO 法，可以得到比前面几种方法精确的刚体旋转矩阵，但对于大应变和大转动问题的误差仍然较大，并且计算更加复杂。同时Timoshenko梁单元的剪切自锁现象也会使得部分变形被放大，从而导致虚假的刚体转动被放大，误差较大。

为了解决上述方法中存在计算精度和效率较低的问题，需对现有的共旋坐标法进行改进。因此，本文在共旋坐标法的框架上，基于改进的空间Timoshenko 梁单元[16]，使用逆向运动方法，剔除结构刚体运动部分，再结合梁单元形函数和截面刚度矩阵得到整体坐标系下的单元切线刚度矩阵。最后，通过多种类型的算例对本文提出的方法和程序进行了较全面和严格的检验。

1 空间梁单元

使用共旋坐标法求解非线性问题时，首先需要求解单元的线刚度矩阵，分析时通常采用插值形函数法构造梁单元，但这些插值函数大多为位移的近似方程，计算往往存在截断误差，导致精度较低。本文采用一种改进的空间Timoshenko 梁单元[16]求解单元线刚度矩阵，具体推导过程如下。

1.1 梁单元横向位移的形函数

对于空间Timoshenko 梁，截面横向位移包含弯曲位移和剪切位移两部分，可以表示为：

式中：v、w分别为梁两个方向总的横向位移；下标b为弯曲变形产生的位移；下标s为剪切变形产生的位移。

对式(1)求一阶导，可得：

式中：E为弹性模量；Iy为截面关于y轴的惯性矩；G为材料剪切模量；A为截面面积；kz为z方向的截面不均匀系数。

将式(3)对x求一阶导，化简之后可得：

由式(5)可知，满足弯曲位移wb的解析解为三次多项式，同理可得到满足vb的解析解也为三次多项式。

1.2 梁单元刚度矩阵

与传统Timoshenko 梁单元一样，梁轴方向的位移u及转角 θx的形函数假设为线性插值，而弯曲位移的插值函数为三次多项式，表达式如下：

通常，Timoshenko 梁单元的应变矢量可以表示为：

根据空间梁单元在x=0,L上的边界条件，可以得到形函数的系数与节点位移之间的关系，其矩阵表达式为：

式中：E(x)为形函数系数向量的系数矩阵；d为节点位移，其表达式为：

把式(13)代入式(10)和式(11)，可得：

最后通过对梁长L的数值积分，得到Timoshenko梁单元的单元刚度矩阵Ke的表达式为：

式中：K11=EA,K22=kyGA，其余参数具体物理意义在HODGES 等[17]和GIAVOTTO 等[18]论文中做出了具体解释。

2 改进共旋坐标法

共旋坐标法的独特之处在于从总体位移中提取弹性变形位移来预先定义投影关系。将梁单元运动从初始状态到最终变形状态分解为刚体运动部分和纯变形部分，其中刚体运动部分包括局部参考坐标系的刚体平移和旋转。因此共旋坐标法的核心问题就是处理不同坐标之间的转换，从而建立纯变形与整体变形之间关系。

对于经典共旋坐标法，一般通过线性插值构造刚体旋转矩阵[19]，当变形较小时，计算结果较为精确，但考虑大应变和大转动问题时则不可忽略计算产生的虚假刚体转动，本文通过使用逆向运动改进共旋坐标法从而减小这一部分所产生的误差。

2.1 空间梁单元的参考坐标系定义与转换

首先定义梁单元相关参考坐标系。

将梁单元的逆向运动分解为两步：一是刚体旋转前后梁单元轴线的转动；二是刚体旋转前后绕着梁轴线的定轴转动。首先求得刚体旋转前后梁的轴向坐标：

2.2 局部坐标系与整体坐标系之间位移向量的转化

定义梁单元整体位移向量为Pgg，去除刚体变形后局部坐标系下位移向量为Pl。通过2.1 节中介绍的旋转框架，从总位移Pgg中剔除刚体位移来计算局部位移Pl。通过两者的转换关系计算局部坐标系下的内力向量fl和切线刚度矩阵Kl，而内力向量在整体坐标系Fg中的表达式，可以通过平衡整体与局部系统中的内部虚功来得到：

式中，r1、r2、r3和 δr1都容易求得，对于 δr3，由式(36)可知与 δq有关。对于共旋法，其辅助向量的定义假设了小的纯变形及其变化且认为辅助向量和r1、r2在同一个平面内，但在求解过程中使用了简单的线性插值函数来求得q。在使用逆向运动求解辅助向量后，辅助向量和r1、r2在同一个平面，求得的刚体转换矩阵更加精确，并且这里不假设小的纯变形，仅仅假设纯变形的增量较小，从而可以求得辅助向量的变化：e

利用求得的切线刚度矩阵计算整体力向量的差值，通过迭代使结果逐渐收敛于精确解，计算流程图如图3 所示。

3 数值算例

为检验本文所提方法的合理性，本文使用MATLAB 软件，编制相应的有限元程序。通过算例1 验证该方法计算平面梁单元所得结果与解析解相比足够接近；算例2 验证该方法可以用于计算不考虑耦合效应的空间梁单元非线性分析；算例3 验证该方法可以用于计算空间耦合梁单元非线性分析；算例4 验证该方法可以用于空间预弯梁单元非线性分析。

3.1 算例1

如图4 所示，悬臂梁在自由端受到横向集中力P的作用，将梁划分成10 个单元，迭代容许误差设定为 10-6，表1 给出了本文的计算竖直位移w、水平位移u及转角 θ0的结果与文献[21]的解析解对比。

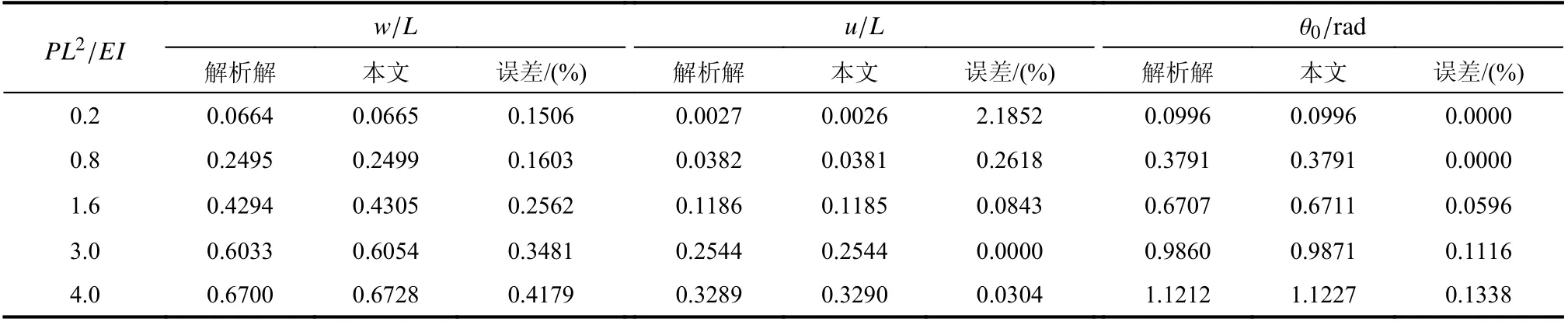
表1 悬臂梁承受集中荷载时的大挠度变形Table 1 Cantilever's large deformation under concentrated load

从表1 结果对比可知，采用改进共旋坐标法计算所得结果与解析解的结果相比，误差基本都小于0.5%，能较为精确的计算悬臂梁在集中荷载作用下的大挠度变形。验证了该方法用于计算平面梁单元非线性分析的正确性。

3.2 算例2

如图5 所示的空间悬臂梁，弯矩M2作用在自由端，大小为：

式中：参数k在0 到2 之间取值。将悬臂梁划分为10 个单元，梁端水平位移为u，竖向位移为v。所得不同弯矩大小作用下图5 所示悬臂梁的变形结果示于图6；表2 给出了本文算法计算的梁端水平位移和竖向位移结果，与解析解[22-24]和文献[25]中HAWC2 方法计算结果进行对比。

从表2 可知，对于悬臂梁承受弯矩作用发生大变形，当k取值从0.4 变化到2.0(即弯矩逐渐变大)，改进共旋坐标法的水平位移计算误差均在0.20%之内，竖直位移计算误差均在1.10%之内，而HAWC2-30 水平位移计算误差多数超过了1.0%，竖直位移计算误差最大达到了22.7%，HAWC2-50 水平位移计算误差多数超过0.4%，竖直位移计算误差最大达到了9.7%，说明本文方法与HAWC2 软件计算结果相比，尤其是大变形情况的位移转角计算，本文方法要更加精确，验证了该方法适用于计算不考虑耦合效应的空间梁单元大转动变形。

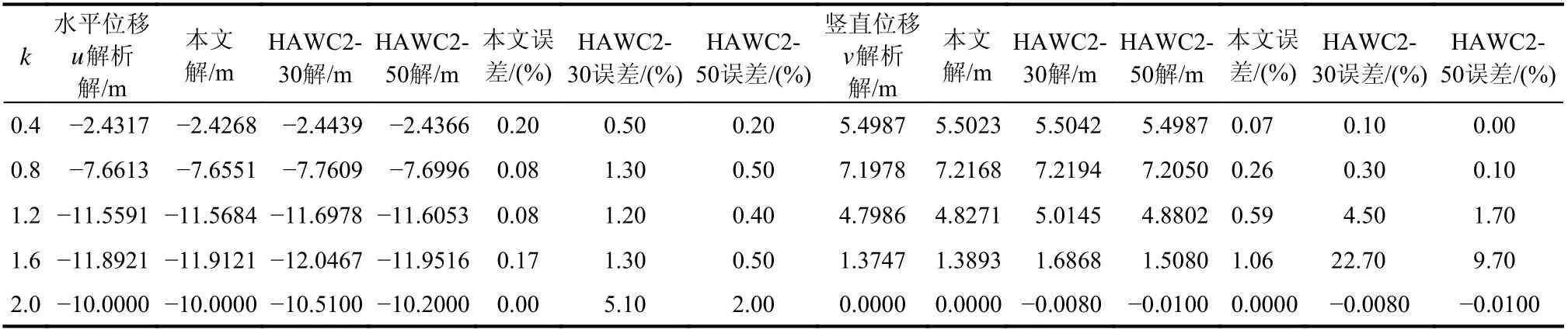
表2 悬臂梁承受弯矩作用的大变形Table 2 Cantilever’s large deformation under bending moment

3.3 算例3

考虑耦合效应的悬臂梁结构如图7 所示，在自由端作用一集中荷载F3=150 N，其耦合的截面刚度矩阵参数详见文献[23]。同样将梁划分为10 个单元，图8 给出了沿梁轴的每个节点的位移和转角所得计算结果。表3 列出了自由端3 个方向的位移和转角与参考文献[7]经典共旋坐标法和HAWC2[25]方法计算结果的对比。

从图8 可知，当耦合梁单元作用一面内荷载时，本文方法能计算出其他方向因耦合作用产生的位移和旋转。从表3 可知，对于考虑耦合效应的空间Timoshenko 梁单元，改进共旋坐标法的计算结果与经典共旋坐标法和HAWC2 软件计算结果相比，误差均有所减小。尤其是对于经典共旋坐标法在计算时因虚假刚体转动产生的较大误差(如本算例中的y方向位移和z方向转角)，使用改进共旋坐标法后这一部分的误差分别减小了2.4%和4.5%，与HAWC2 计算结果相比除z轴误差扩大了0.36%外，其他位移和转角结果均较好，尤其是HAWC2 方法计算误差较大的y方向位移和x方向转角，误差分别减小了约3.6%和2.3%，验证了该方法适用于计算考虑耦合效应的空间Timoshenko 梁单元的变形。

表3 自由端位移和转角参数比较Table 3 Comparison of tip displacements and rotations

3.4 算例4

如图9 所示，一个 45°的悬臂圆弧梁，圆弧半径R=100 m，在自由端受到竖向集中荷载F=600 N的作用，截面刚度矩阵详细参数见文献[26]所示，表4 列出了本文计算的梁自由端三个方向位移x、y、z计算结果与解析解[26]、经典共旋坐标法的计算结果[7]以及商用软件HAWC2[25]的计算结果的对比分析。

从表4 可知，对于预弯的空间Timoshenko梁，改进共旋坐标法的计算结果与经典共旋坐标法相比，三个方向位移的误差分别减小了0.2%、0.9%、0.1%，与HAWC2 计算误差较小的结果相比本文方法也能较为精确的求得，而HAWC2 计算误差较大的x和y方向位移，本文方法误差分别减小了1.9%和1.8%，验证了该方法适用于计算预弯式悬臂梁的大变形，也为后续研究预弯风力机叶片结构提供了研究基础。