网格箍筋约束混凝土柱轴压受力性能试验研究

万宇通，郑文忠，王 英

(1. 哈尔滨工业大学结构工程灾变与控制教育部重点实验室，哈尔滨 150090；2. 哈尔滨工业大学土木工程智能防灾减灾工信部重点实验室，哈尔滨 150090)

人们对约束混凝土的研究已有一百多年，其中RICHART 等[1]提出以相对侧向约束应力来表征约束混凝土峰值压应力和峰值压应变的方法，SHEIKH 等[2]提出由“拱作用”确定有效约束应力的方法，为后续对约束混凝土受压性能的研究奠定了重要基础。国内外学者结合理论和经验提出了许多不同形式的约束混凝土受压应力-应变模型：MANDER 等[3]提出了上升段和下降段方程形式统一的模型；RAZVI 等[4]完善了包括抛物线上升段、直线下降段和水平残余应力段的三段式模型；BOUSALEM 等[5]弱化混凝土强度影响，改进三段式模型应用于矩形箍筋约束混凝土。张秀琴等[6]将素混凝土应力-应变曲线方程形式用于约束混凝土；赵作周等[7]对已有模型进行改进得到了ZSA模型；赵宪忠等[8]基于Mander 模型建立了钢骨混凝土不同约束区域的应力-应变模型，并通过有限元分析进行了对比验证。但各种模型由于试验测量方法不同[9]、方程形式不同、适用范围不同等原因，往往存在较大差异，且存在考虑影响因素不全面、模型曲线不平滑等问题。

随着混凝土强度提高，人们对约束混凝土的研究中使用的箍筋强度也在不断增加，箍筋的形式也越来越复杂。根据史庆轩等[10-11]的研究：体积配箍率、箍筋屈服强度和形式对高强箍筋约束混凝土的性能有重要影响；在体积配箍率相近情况下，复合箍筋的约束效果比单箍好。现如今，网格箍筋已经成为工程中主要应用的箍筋形式，而《混凝土结构设计规范》(GB50010-2010)[12]中仅考虑了配置螺旋式或焊接环式间接钢筋的钢筋混凝土受压构件中箍筋约束对正截面受压承载力的提高，没有考虑网格箍筋的约束作用。因此，本文根据39 个网格箍筋约束混凝土方柱的试验数据，考察了混凝土轴心抗压强度、箍筋屈服强度、体积配箍率等参数对网格箍筋约束混凝土的峰值压应力、峰值压应变以及受压应力-应变曲线的影响，获得了网格箍筋约束混凝土峰值压应力、峰值压应变及受压应力-应变曲线的数学表达，提出了极限压应变计算方法，为网格箍筋约束混凝土柱的设计与非线性分析提供参考。

1 试验概况

本文设计制作了39 个网格箍筋约束混凝土方柱，见图1，主要设计参数见表1。试件箍筋保护层厚10 mm；纵筋根据箍筋形式选用8 根或12 根直径10 mm 的HRB400 钢筋；试件中部试验区段高500 mm；为避免试件端部先发生局部破坏，在柱顶部和底部分别设置高400 mm，箍筋间距40 mm的箍筋加密区。

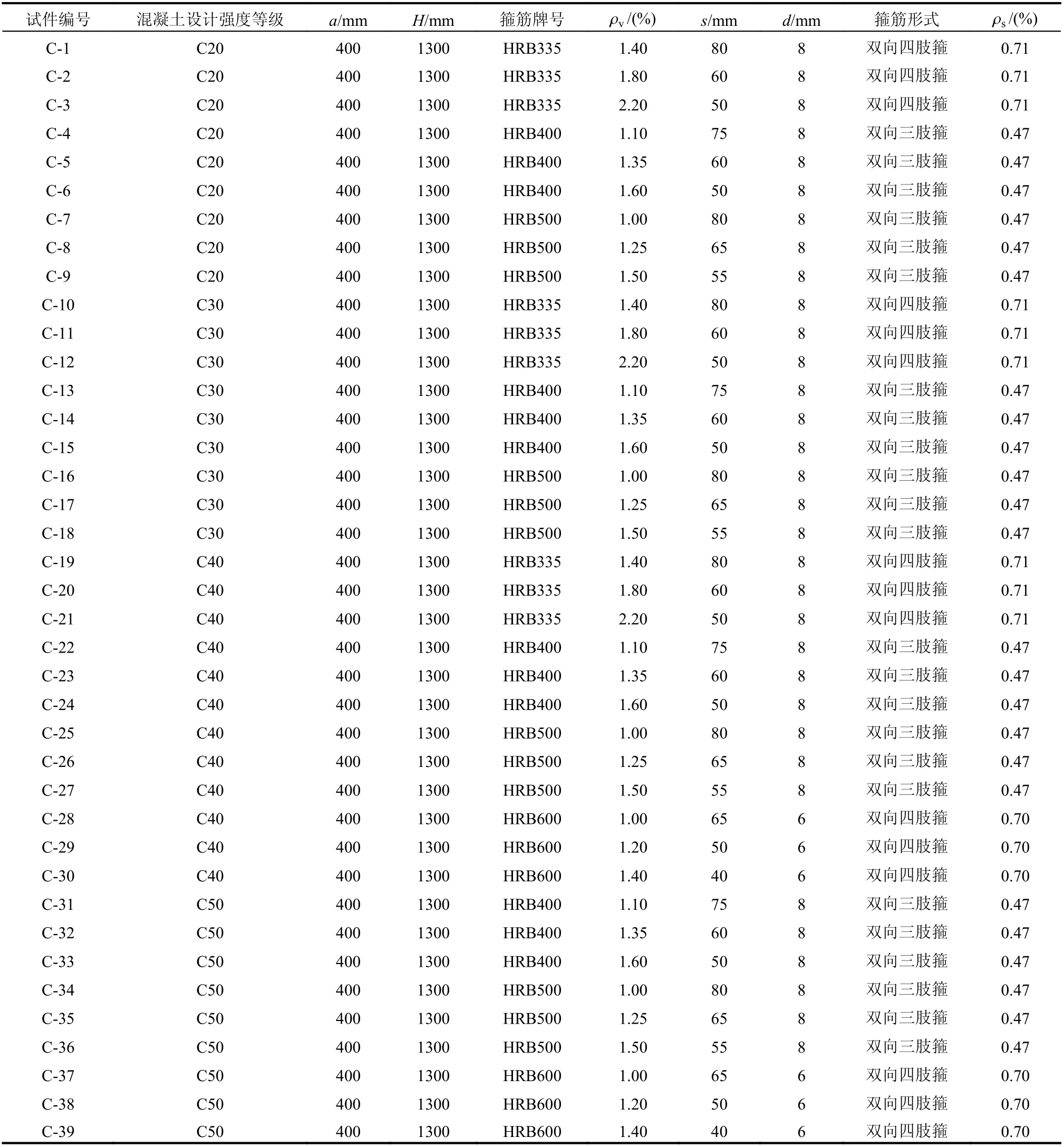
表1 试件设计参数Table 1 Design parameters of specimens

试验使用的混凝土基本力学性能见表2，热轧钢筋的基本力学性能见表3。

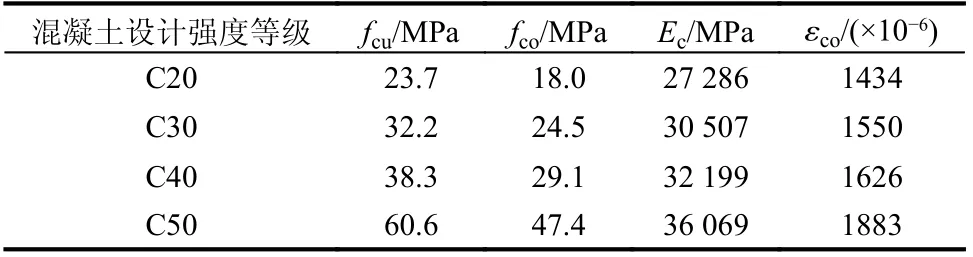
表2 混凝土基本力学性能Table 2 Basic mechanical properties of concrete

表3 钢筋基本力学性能Table 3 Basic mechanical properties of steel bars

为测量网格箍筋应变，混凝土浇筑前，在试件非加密区中部的相邻4 圈箍筋表面粘贴钢筋应变片，每圈在箍筋形成的其中一个网格中布置4 个，共16 个，标记为1～16，钢筋应变片均布置于箍筋近边端如图2 所示。

在哈尔滨工业大学交通学院结构试验大厅的YAW-10000J 试验机上进行加载。加载前，为测量约束混凝土轴向压应变，在试件相对的两个侧面中部试验区段沿轴向粘贴混凝土应变片，并在四个侧面分别布置标距为250 mm 的自制应变引伸计。自制应变引伸计由支座和电阻式位移计组成：通过植筋的方式安装支座(植入深度50 mm)，将带有接长杆的电阻式位移计固定在支座上。为防止试件端部先于试验区段破坏而在试件上下端部加设方形钢套箍。为保证试件受力均匀且轴心受压，对试件底面及顶面使用石英砂找平，并在柱顶与试验机上压板之间设置球铰。加载装置见图3 和图4。

2 试验现象与结果

各试件试验现象基本一致：加载初期，未出现明显现象，试件表现出线弹性；当荷载增大至80%～100%峰值荷载时，试件表面出现细小竖向裂缝；当荷载达到峰值荷载附近时，试件表面裂缝发展连通，棱部裂缝较宽，可听到因混凝土开裂产生的“噼啪”声，如图5(a)所示；当荷载下降至100%～70%峰值荷载时，试件表面有混凝土碎粒沿裂缝剥落，如图5(b)所示；当荷载下降至70%～50%峰值荷载时，保护层酥碎，暴露出箍筋、纵筋和核心混凝土，如图5(c)所示；随着变形继续发展，纵筋发生屈曲，部分试件有箍筋在纵筋屈曲处附近被拉断，荷载急剧下降；加载结束后，观察到试件中部破坏段的箍筋被撑圆，如图5(d)所示。

约束混凝土柱所承受的轴向荷载由核心约束混凝土、核心外非约束混凝土和纵向钢筋三部分分担。假定纵筋与混凝土粘结良好，没有相对滑移，即纵筋压应变与约束混凝土压应变保持一致，则核心约束混凝土承担的轴向荷载可按照式(1)进行计算。

式中：Fcor为核心约束混凝土分担的压力；N为试件承担的总压力；As为纵筋总截面面积；σs为纵筋的压应力；A为试件全截面面积；Acor为试件核心截面面积；σco为核心外非约束混凝土的压应力。

其中纵筋的应力-应变关系按照《混凝土结构设计规范》(GB 50010-2010)[12]中建议的钢筋本构关系简化为三段式。核心外非约束混凝土的应力-应变关系参考MANDER 等[3]的假设：核心区域外混凝土应力-应变曲线在压应变小于2 倍素混凝土峰值压应变时，与素混凝土单轴受压应力-应变曲线相同；在压应变大于2 倍素混凝土峰值压应变时为一条直线；在压应变达到剥落应变后为零。

根据式(2)计算各试件核心约束混凝土压应变为εcc时的压应力σcc(εcc)，分别绘制受压应力-应变曲线，见图6。

各试件参数和试验结果统计见表4，其中约束程度的划分依据文献[13]：有效约束应力与素混凝土轴心抗压强度之比小于等于5%时为低约束，大于5%且小于等于20%时为中约束，大于20%时为高约束；按国家现行规范要求的最小配箍特征值计算得到的约束程度主要为低约束和中约束。

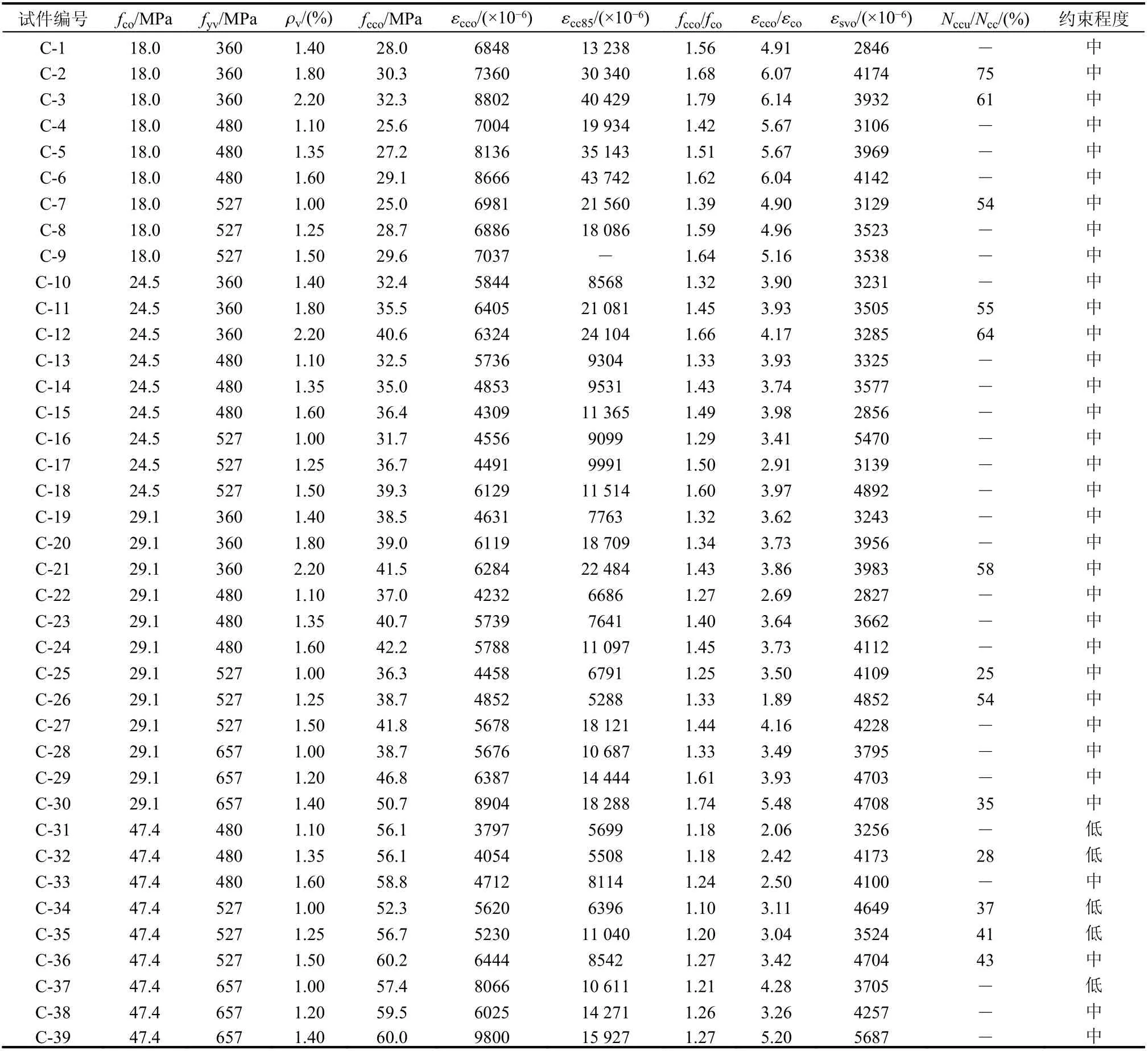
表4 试件参数及试验结果Table 4 Parameters and test results of specimens

3 约束混凝土受压应力-应变模型

3.1 关键因素对约束混凝土轴心受压性能的影响

对箍筋屈服强度均为480 MPa、体积配箍率均为1.1%，而素混凝土轴心抗压强度分别为18.0 MPa、24.5 MPa、 29.1 MPa、 47.4 MPa 的4 个 试 件(C-4、C-13、C-22、C-31)的试验结果进行分析，如图7 所示。其余参数相同时，随着素混凝土轴心抗压强度fco的提高，峰值应力提高幅度fcco/fco降低，峰值应变提高幅度εcco/εco降低，应力-应变曲线下降段变陡。主要原因是：箍筋约束作为被动约束方式发挥约束作用依赖于混凝土的横向变形。而混凝土强度越高，轴向受压时轴向压应变和横向拉应变都相对越小；且一定轴向压应力水平下，轴向与横向的塑性变形也随混凝土强度提高而相对减小。因此，素混凝土轴心抗压强度越高，箍筋约束作用相对越弱。

对素混凝土轴心抗压强度均为18.0 MPa、箍筋屈服强度均为370 MPa，而体积配箍率分别为1.4%、1.8%、2.2%的3 个试件(C-1、C-2、C-3)的试验结果进行分析，如图8 所示。其余参数相同时，随着体积配箍率ρv增大，fcco/fco和εcco/εco增大，约束混凝土受压应力-应变曲线下降段变缓。主要原因是：体积配箍率越大，则箍筋数量越多，间距越小，提供的有效侧向约束应力越大，约束作用越强[14,15]。

对素混凝土轴心抗压强度均为29.1 MPa、体积配箍率均为1.4%而箍筋屈服强度分别为370 MPa、661 MPa 的2 个试件(C-19、C-30)的试验结果进行分析，如图9 所示。其余参数相同时，对于约束混凝土达到峰值应力时箍筋拉应力达到屈服强度的试件，随着箍筋屈服强度fyv提高，fcco/fco和εcco/εco增大，约束混凝土受压应力-应变曲线下降段变缓。主要原因是：箍筋强度得到充分发挥时，其屈服强度越高，提供的有效侧向约束应力越大，约束作用越强。

综上所述，随着配箍特征值增大，网格箍筋约束混凝土峰值压应力和峰值压应变提高幅度增大，受压应力-应变关系曲线下降段变缓。

3.2 峰值压应力和峰值压应变计算公式

根据力学分析，约束混凝土在箍筋拉应力为σsv时受到的约束应力可按式(3)计算。

式中：σl为侧向约束应力；σsv为箍筋拉应力。

引入有效约束系数ke(有效约束区最小截面面积与核心截面面积之比)[3]，综合考虑箍筋间距、箍筋肢距和截面尺寸对网格箍筋约束效果的影响，将式(3)得到的约束应力折减。箍筋提供的有效约束应力σle和有效约束系数ke可分别按式(4)和式(5)计算。

式中：bi为纵筋净间距；s′为箍筋净间距；acor为核心截面边长。

若约束混凝土峰值压应力下箍筋拉应力达到其屈服强度，将fyv代入式(4)，此时箍筋提供的有效约束应力fle可按式(6)计算。

许多学者基于不同的混凝土破坏准则建立了约束混凝土峰值压应力计算公式：Mohr-Coulomb强度准则[1]、William-Warnke 五参数破坏准则[3,16]、Ottossen 四参数破坏准则[17]、双剪统一强度理论[18]等。其中Mohr-Coulomb 强度准则和双剪统一强度理论的子午线为直线，与实际情况不符，但形式简单，应用方便，在一定范围内计算结果与试验结果保持良好一致。考虑到本文试验中静水压力水平不高，约束混凝土峰值压应力与有效约束应力表现出良好的线性关系，因此采用RICHART 等[1]提出的公式形式，对本文39 组试验数据进行统计分析(如图10 所示)，得到网格箍筋约束混凝土的峰值压应力fcco、峰值压应变εcco计算公式：

式(7)、式(8)回归分析的R2分别为0.99 和0.97。

3.3 下降段参数计算公式

使用与3.2 中类似的方法，对本文39 组试验数据进行统计分析，得到网格箍筋约束混凝土压应力下降至85%峰值应力对应的压应变εcc85和50%峰值应力对应的压应变εcc50计算公式：

式中，εc85为素混凝土压应力降至0.85fco对应的压应变。

该计算公式的回归分析的R2为0.90。

3.4 约束混凝土应力-应变曲线方程

根据本文试验所得39 条实测曲线，建立网格箍筋约束混凝土受压应力-应变模型。上升段形式选择Popovics 模型[19]，下降段形式选择过镇海模型[20]，则该模型的曲线方程为：

3.5 极限压应变

约束混凝土的极限压应变对确定其受压应力-应变曲线的有效段具有重要意义[21]，但其仍未有统一的定义。

纵筋屈曲后分担的荷载下降，易造成核心混凝土被压溃，使构件承载力迅速下降，是钢筋混凝土构件的一种后果严重且难以修复的破坏现象。因此，本文将把纵筋屈曲作为确定约束混凝土极限压应变的考虑因素。

试验过程中保护层混凝土与约束混凝土发生分离后不会立即脱落，纵筋发生屈曲时刻难以准确记录，所以引入DHAKAL 等[22]提出的D-M 钢筋屈曲模型(该模型将发生屈曲的钢筋视为相应的单轴材料，适用于单轴加载，与本文试验情况相符)中间点的钢筋平均压应变，等效为考虑纵筋屈曲的约束混凝土极限压应变εccu1，表达式见式(15)。

式中：ε*为D-M 钢筋屈曲模型中间点的钢筋平均压应变；fy为纵筋屈服强度；s为箍筋间距；d为纵筋直径；εy为纵筋屈服应变。

对于素混凝土强度较高而受到箍筋约束作用较弱的试件，约束混凝土压应力达到峰值后退化相对较快，考虑纵筋屈曲的极限压应变则不适用。因此将约束混凝土压应力降至0.5fcco时的压应变定义为εccu2，由受压应力-应变曲线方程，即式(10)～式(13)可得：

综上所述，可将网格箍筋约束混凝土极限压应变εccu定义为：

使用式(17)对本文设计制作的39 个试件进行计算，得到的极限压应变范围为1.8%～7.2%。

由本文试验结果可知，39 个试件中有7 个试件(配箍特征值为0.23～0.45)的箍筋发生破断时，试件承担的轴向荷载高于50%峰值荷载，此时约束混凝土的压应变介于3.2%～15.7%，均远大于计算所得的极限压应变。

3.6 约束混凝土应力-应变曲线的比较

为了验证本文模型能否合理反映网格箍筋约束混凝土应力-应变关系特征，选择Mander 模型[3]、Saatcioglu 模型[23]、钱稼茹模型[24]等三种具有代表性的箍筋约束普通强度混凝土应力-应变关系模型以及本文模型分别对本文设计制作的网格箍筋约束混凝土试件进行计算，可得四种模型曲线与试验曲线的比较，部分如图11 所示。

经对比可知，本文模型曲线上升段与实测曲线基本吻合，大部分试件的下降段与实测曲线也吻合较好，对网格箍筋约束混凝土受压应力-应变关系的反映明显优于其他三种模型。

4 结论

通过39 个网格箍筋约束混凝土方柱的轴心受压试验研究其轴压受力性能，基于试验结果得出以下结论：

(1) 约束混凝土压应力达到峰值时，受压试件的约束箍筋屈服；随着配箍特征值增大，网格箍筋约束混凝土fcco/fco和εcco/εco提高，受压应力-应变曲线下降段变缓。

(2) 拟合得到了适用于混凝土轴心抗压强度为18.0 MPa～47.4 MPa，箍筋屈服强度为370 MPa～661 MPa，体积配箍率为1.0%～2.2%的网格箍筋约束混凝土的峰值压应力、峰值压应变计算公式，建立了相应的受压应力-应变关系模型；提出了综合考虑纵筋屈曲和约束混凝土压应力退化的约束混凝土极限压应变计算方法。