一种抗震性能化设计方法及在防屈曲支撑钢框架结构中的应用
2022-11-05邱灿星杜修力
邱灿星,杜修力
(北京工业大学城市与工程安全减灾教育部重点实验室,北京 100124)
防屈曲支撑(BRB)拥有出色的消能能力和稳定的拉压滞回行为,自问世以来持续吸引着各国学者的研究兴趣[1],并在我国和世界上其他地震多发区均有广泛的实际工程应用[2]。在开展抗震分析和试验研究的同时,学者们也在积极发展抗震设计方法。尤其是在基于性能的地震工程[3]这一范畴下,设计方法更加聚焦于结构的性能,这使得性能化设计方法的研究成为地震工程界的学术热点。尽管规范中仍然普遍采用基于力的设计方法,但是基于位移的设计方法往往更为高效,因为设计时以结构的位移为出发点,直接考虑了结构主体和非结构成分的损伤与位移需求之间的联系,从而能够减少设计过程的迭代验算次数。因此,基于位移的设计方法成为抗震性能化设计方法的研究趋势[4]。
在抗震性能化设计方法的发展历程中,PRIESTLEY 等[5]提出了直接基于位移的抗震设计(Direct displacement based design, DDBD),该方法给出了等效刚度和等效阻尼比的计算公式,具有较好的普适性而被广泛应用于各类结构的抗震设计中。例如,李钢和李宏男[6]将该方法引入到消能减震结构中。杨博雅和吕西林[7]使用该方法设计了预应力预制混凝土剪力墙结构。简斌等[8]将该方法设计了预应力混凝土框架结构。徐龙河和杨雪飞[9]采用该方法对自复位支撑钢框架结构进行了参数设计和分析。
与此同时,学术界还基于不同的理论提出了多种抗震性能化设计方法。例如,李国强和冯健[10]研究了支撑钢框架在罕遇地震下的弹塑性位移增大系数,提出了抗震设计时进行罕遇地震下弹塑性位移验算的实用计算数表。王伟等[11]假设结构的层间位移是均匀的,为支撑钢框架提出了简化抗震设计方法。LIU 等[12]回归了强度系数与非线性位移比的函数关系,并用以设计自复位支撑钢框架。QIU 和ZHU[13]为自复位支撑钢框架提出了塑性设计方法和能量设计方法[14]。
具体到BRB 结构,相关的抗震性能化设计方法同样是国内外学者们长期以来的研究课题。例如,TERAN-GILMORE 和VIRTO-CAMBRAY[15]结合位移反应谱提出了一种基于位移的设计方法。白久林等[16]和潘毅等[17]分别提出了基于能量平衡的抗震塑性设计方法和基于剪力比的抗震设计方法,二者均以BRB 钢筋混凝土框架为例进行了验证。贾明明等[18]、SAHOO 和CHAO[19]分别提出了基于延性的设计方法和塑性设计方法,二者均以BRB 钢框架为例予以了论证。
综合上述抗震设计方法,它们存在的共同问题有:1)性能目标单一,大都仅以峰值层间位移角(θp)为设计目标,鲜有文献探索如何将残余层间位移角(θr)纳入设计目标[20];2)同时考虑θp和峰值楼面加速度(PFA)的设计方法也不多。事实上,结构主体和非结构成分的损伤与θp、θr和PFA均有直接联系。因此,结构的抗震性能目标应该是多元的。在某种程度上,抗震性能化设计在本质上可以理解为设法将结构的θp、θr和PFA 同时控制在目标范围以内。
为此,本文借鉴文献[21]的思路,先通过单自由度(SDOF)体系的弹塑性时程分析总结BRB结构的地震响应规律,然后以结构动力学为理论基础,将基于SDOF 的结果推广至多自由度(MDOF)体系,即本文中的多层BRB 框架结构。在建立设计方法时,将θp、θr和PFA 这三项地震响应均选为性能目标,并结合规范和文献定义合理的目标值,从而为BRB 结构发展出一种新的抗震性能化设计方法。为了演示和论证该设计方法,本文选取了一栋六层BRB 钢框架结构地基准模型,为之开展了抗震设计和性能评估。本文的方法对于其他各类结构的抗震性能化设计也有一定的借鉴价值。
1 BRB
如图1 所示,典型的BRB 一般包括提供屈曲约束效果的外包钢管和侧向变形受限制的低屈服点核心钢构件。为了减轻摩擦,通常在砂浆等填充材料与核心钢构件之间使用无粘结材料。在轴向压力作用下,外围的钢管可为核心钢构件提供可靠的约束效果而避免内芯出现侧向屈曲失稳。通过该受力机制,BRB 在拉压荷载作用下都可呈现出稳定的承载力和耗能能力,从而显著提高了构件的抗震性能。BRB 的研究和应用可参见有关综述[1-2],本文不作过多赘述。如果假设支撑的连接方式可靠且连接段的刚度较大,则BRB 构件的抗震设计可以等同为确定核心钢构件的工作段长度L和横截面积A,如图1 所示。
2 SDOF 体系
为了初步掌握BRB 钢框架的地震响应规律,本节针对等效SDOF 体系开展了弹塑性时程分析。基于SDOF 体系所得到的结果将推广至MDOF 体系,并用于发展抗震性能化设计方法。图2(a)所示为BRB 结构的SDOF 体系;图2(b)包括了弹性体系和弹塑性体系的荷载-位移曲线以及设计谱。为衡量弹塑性体系的屈服力,采用强度折减系数R[22]关联其与相应弹性体系最大地震力的关系,定义如下:
式中:Fel为弹性体系的最大地震力;Fy为弹塑性体系的屈服力;m为体系的质量;Sa为对应于结构固有周期的谱加速度,该值可从设计谱上直接读取。
以下是BRB 结构SDOF 体系的结构动力学方程:
式中:x为体系与地面的相对位移;x¨g(t)为地震动的加速度时程;ζ 为阻尼比;ωn为固有频率;k为初始刚度;f(x)描述了体系的滞回行为,在本文中简化为双线性弹塑性本构模型。在SDOF 体系的分析中,变化的参数包括固有周期T(T= 2π/ωn)和R;其中T值的范围为0.1 s~2 s,以0.1 s 为间隔;综合考虑以往文献[13 - 14]中采用的R值,本文中的R值取为4、6、8 和10。
在SDOF 体系的分析中,关注的地震响应包括峰值位移(xp)、峰值加速度(Ap)、残余位移(xr)和延性系数(μ)。其中:xp与结构主体和非结构成分的损伤有直接联系;Ap主要与加速度敏感型的非结构成分的损伤程度有关;xr则直接衡量了结构震后修复的难易程度;μ将用于估计PFA 的大小。上述四项指标的定义如下:
式中:tD为弹塑性时程分析的总时间;为准确计算xr,在每条原始地震动后添加持时为10 s 的零加速度序列;xy为结构的屈服位移。
3 地震动
本文假设结构位于美国加州洛杉矶地区,因而选取了文献[23]给出的地震动。这些地震动将被用于SDOF 体系和BRB 框架结构的弹塑性时程分析。该组地震动总共有20 条,对应于该地区50年内超越概率约为10%的地震烈度。根据文献[23]的报道,该组地震动由10 条历史地震记录通过调整频率成分和调整PGA 幅值而生成。
图3 绘制了SDOF 体系的单条反应谱、该组地震动的平均反应谱和对应于该地区场地条件的设计谱。需要说明的是,根据《建筑抗震设计规范》(GB 50011-2010)[24]的规定,钢结构在罕遇地震下的弹塑性分析,体系的阻尼比可取为5%。可以看到,尽管各条地震动之间存在着显著的差异,但是平均反应谱与设计谱吻合良好。因此,鉴于地震响应的高度离散性,下文的分析中将着重关注结构的平均响应。
4 SDOF 体系的计算结果
SDOF 体系的弹塑性时程分析在抗震分析开源平台OpenSees[25]中进行。图4 给出了SDOF 体系在20 条地震动作用下各响应的平均值及其随T和R的变化规律。
图4(a)所示为xp的计算结果。xp随着T的变长和R的增大而增大,这主要是因为长周期的结构变形较大,并且R越大意味着体系的屈服强度越低,体系更容易屈服而呈现出更大的位移需求。
图4(b)显示了μ随着T和R变化的规律。当T<0.5 s 时,μ随T的减小而迅速增大,这是因为在短周期范围内,弹塑性结构的屈服位移非常小。例如,假设结构的R=8,当T=0.3 s 时,弹塑性结构的屈服位移为0.0038 m,尽管峰值位移的平均值仅为0.08 m,但是结构的延性需求却高达21。当R增大时,结构的xp增大,而xy减小,二者的共同效应使得μ增大。
图4(c)为xr的计算结果。可以看到,与xp和μ相比,xr表现出更为显著的不确定性。当T<0.8 s时,xr随T的变长而近似于线性增加,但是几乎不受R值变化的影响;当T在0.8 s~1.5 s 时,xr随T的增大而轻微减小,但是随R的增大而减小;当T在1.5 s~2.0 s 时,xr随T的增大而增大,但R的影响则较为随机。综合以上观察,可以归咎为残余位移自身就是高度不确定的地震响应,这在前人的研究中亦多次观察到类似的现象[20-21]。
图4(d)为Ap的计算结果。可以看到,长周期结构的加速度较小;当R增大时,Ap在整个周期范围内都稳定地减小,这是因为Ap与体系的屈服强度相关。
5 设计步骤
第4 节通过SDOF 体系的弹塑性时程分析得到了BRB 结构的地震响应规律。本节详细介绍抗震性能化设计方法。对于本文的中心支撑钢框架结构,BRB 是其核心抗震元件。借鉴文献[26]做出的假设,本文同样假设BRB 为结构体系提供所有地抗侧力和消能能力;同时,结构主体的梁和柱仅承受竖向荷载和BRB 的反力,并通过能力设计的原则保持弹性。因此,该支撑框架结构的抗震设计落脚于确定各个层楼中BRB 核心钢构件的A和L。该抗震设计方法的具体过程参考了文献[21]的思路,其各个步骤阐述如下:
1)获取结构信息。在设计阶段的初期可以获得:第i层的楼层质量mi和层高hi。结构的总质量M和总高度Hn计算如下:式中,n为楼层总数。
2)确定BRB 核心钢构件的屈服应力σy和弹性模量E。该步骤可由查阅文献或试验测试完成。
3)估计结构的基本周期。由于本文假设结构位于美国洛杉矶地区,因此,采用标准[27]给出的周期估计公式:
式中:Ct= 0.0731 和x= 0.75 为标准[27]给BRB 钢框架结构定义的取值。需要注意的是,根据式(9)估计的周期与实际周期可能有误差。
4)开展SDOF 体系的弹塑性时程分析。通过参数分析建立R-T-xp、R-T-μ、R-T-xr和R-T-Ap的关系。图4 所示即为相应结果。
5)确定设计目标的取值。设计目标包括θp、θr和PFA。在基于性能的地震工程范畴下,性能目标可根据设计人员、甲方或业主等的意愿合理取值。在本文中,根据标准[27]的规定,定义θp=1.5%;根据文献[28]定义的修复极限,定义θr=0.5%;根据文献[13]的建议,定义PFA=1.0g。
6)估算结构的整体地震响应。假设结构在一组地震动作用下的平均地震响应沿建筑高度方向呈均匀分布,且结构在地震作用下的振动由一阶振型控制并保持不变,则有以下各式:
式中:θp_r和θp_s分别为屋顶和楼层的峰值位移角;θr_r和θr_s分别为屋顶和楼层的残余位移角;μs和μb分别为结构和支撑的延性需求;PFAmax为所有楼层中峰值楼面加速度的最大值。
7)建立SDOF 体系与MDOF 体系(即BRB 结构)之间的联系。根据结构动力学理论[29],有如下关系式:
式中: Γ1为一阶模态的振型参与系数; φr1为一阶振型在结构顶层的分量,其计算方式来源于标准[27];wi和wn分别为第i层和第n层的楼层重量;Hi和Hn分别为第i层和第n层距离地面的高度;k为与结构周期相关的指数。通过式(14)可以反推出SDOF体系的xp。
同样的,假设结构的平均残余层间位移角沿楼层高度均匀分布,则有如下关系式:
通过式(16)可以反推出SDOF 体系的xr。
至于楼面加速度的估计,SDOF 体系和MDOF体系之间的关系无法按照式(14)和式(16)直接建立。为此,本文采纳文献[30]给出的计算公式:
式中:Teff为考虑了结构非线性的有效周期;Tmax为有效周期的最大值;α 为屈服后刚度。文献[30]中的研究对象为抗弯钢框架,定义Tmax=2.5 s;本文考虑到BRB 钢框架的延性更高,故假设Tmax=3.0 s。比值z/Hn为楼层的正则化高度。根据式(18)不难得知,文献[30]认为结构的最大楼面加速度将出现在顶层,其值为:
通过式(17)~式(19)可以反推出SDOF 体系的μ。
8)确定R和μ。步骤7)已经反推出SDOF 体系的地震响应,而结构的T可由式(9)估算,再根据图4 即可找出同时满足xp、xr和Ap的R值和μ值。
9)计算基底剪力(V)。当R确定后,结构的设计基底剪力计算如下:式中,Sa根据预估的T从设计谱直接取值。
10)计算各楼层的水平地震作用(Fx)。本文根据标准[27]的方法,将基底剪力沿高度方向分配于各个楼层:
式中:wx为第x层的楼层重量;Hx为第x层距离地面的高度。
11)计算第i层BRB 的横截面积(Ai)。假设结构体系的抗侧向承载力和消能能力完全由支撑提供[25]。因此,由式(21)计算所得的层间剪力将完全由支撑抵抗。本文中的支撑为“人”字形布置,那么,第i层支撑所需的Ai可按照式(23)计算所得:
式中,θi为第i层的支撑与水平面的夹角。
12)计算第i层BRB 的工作段长度(Li)。由于假定了结构的变形沿楼层高度均匀分布,因此各层支撑也应该同时屈服。因此,第i层支撑的Li可按下式计算所得:
13)检查设计结果。开展结构在地震作用下的弹塑性时程分析和抗震性能评估,并检验实际地震响应的均值是否与性能目标相吻合。
14)若实际地震响应的均值与设计目标差别较大,则根据误差的正负和大小调整支撑的尺寸,直到满足设计要求。
6 结构原型
为了演示和验证提出的设计方法,本文根据场地信息选取了一栋六层BRB 钢框架结构的基准模型[31]。图5 展示了该结构模型的平面布置和立面。可以看到,结构具有对称的平面布置,在两个正交方向各有6 榀支撑框架。每跨的跨度为9.14 m,结构首层的层高为5.49 m,其他层的层高为3.96 m。原模型的梁柱节点为刚节点,本文改为铰节点,目的是提高节点的转动能力,同时释放了节点对支撑的转动约束,反过来也减轻了节点区域的损伤。柱底和地面固定连结,可以形成二道防线,进一步提高体系的抗震性能。
按照本文的设计方法,当设计目标确定后,即θp、θr和PFA 为已知值,根据式(14)~式(19)反推出SDOF 体系的xp、xr、μ和Ap;当SDOF 体系的地震响应确定后,再根据图4 找出能够同时满足要求的R和μ。在本文所选的例子中,结构的设计参数最终确定为:R= 8 和μ= 14.8。表1 列出了各层BRB 的力学性能,包括屈服强度和轴向刚度。待BRB 设计完成后,结构的梁和柱根据能力设计的原则确定尺寸。需要说明的是,由于本文的设计方法与文献[31]不同,这使得支撑和梁柱构件的尺寸有所变化。图5(b)给出了框架梁柱构件的信息,为了和标准[27]统一,采用了美标[32]宽翼缘工字钢。
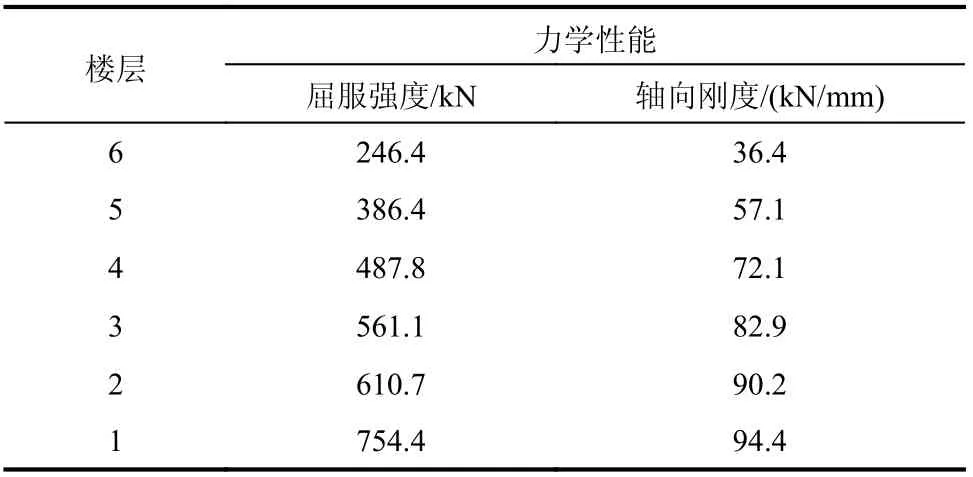
表1 BRB 的力学性能Table 1 Mechanical properties of BRB
与SDOF 体系的计算一样,BRB 钢框架结构的弹塑性时程分析也在OpenSees[25]中进行。图5(b)所示为结构的数值模型。由于结构是对称的且地震只在X方向输入,因此,建模时无须考虑结构的扭转变形。数值模型包括BRB 框架和重力柱两部分,其中重力柱的功能在于产生惯性力和模拟P-Δ效应。在地震动输入方向共有6 榀支撑框架,因此,该数值模型承担1/6 的楼层质量。
梁和柱的铰节点以及支撑与框架的铰接,均通过耦合两个在空间上重合的节点位移来实现。假定楼板为刚性,这通过耦合梁两端的节点位移来实现。与SDOF 体系的分析一致,结构的前两阶瑞利阻尼比设置为5%。梁和柱均由一个force BeamColumn 单元模拟,并赋予Steel02 的材料,其屈服应力和屈服后刚度比分别为345 MPa 和0.3%。BRB 只受轴力作用,采用Truss 单元模拟,并赋予Steel01 的材料,其屈服应力和屈服后刚度比分别为235 MPa 和1%。
7 抗震性能评估
7.1 非线性静力分析
为掌握结构体系的基本力学行为,在进行弹塑性时程分析之前,本节对BRB 结构先进行非线性静力分析,即推覆分析。推覆前先获取结构的一阶模态,然后沿楼层高度方向施加与结构一阶模态相吻合的侧向力,并在推覆过程中保持不变。推覆时,以屋顶的水平位移为控制点,当屋顶的水平位移角达到4%时,推覆过程结束。
图6 所示为推覆结果,可以清晰地观察到结构从弹性发展至显著塑性的完整过程。图6(a)是屋顶位移角与基底剪力/结构自重的关系曲线。随着推覆位移的不断增大,结构在屋顶位移角约为0.18%时屈服;推覆曲线整体上表现出双线性行为,这与BRB 自身的力学行为一致。图6(b)则是当屋顶位移角达到4%时结构的侧向变形,该图也反映了不同楼层的相对变形。通过该图可以知道,与其他层相比,第2 层~第4 层的变形增长量较大,这意味着这三层可能是潜在的薄弱层,有待于弹塑性时程分析予以验证。
7.2 非线性动力分析
本节开展结构的非线性动力分析,即弹塑性时程分析。如前所述,本文所关注的地震响应为θp、θr和PFA。当结构受到如图3 所示的地震动作用后,地震响应的超越概率分布如图7 所示。由图7 可知,三项响应均呈现出较好的对数正态分布规律。在设计时已经提及,θp、θr和PFA 的目标值分别为1.50%、0.5%和1.0g;根据拟合曲线(图7 中的黑色实线),三者的实际均值分别为1.56%、0.6%和0.58g。由此可知,θp和θr各自均与性能目标值非常接近;然而,PFA 却与性能目标值有一定的差距,偏于安全。因此,本文的设计方法可较好地使结构同时满足θp和θr这两项性能目标的要求;但是结构的PFA 偏于保守,这可能是楼面加速度的估算方法不适用于本结构,即式(17)~式(19)带来了误差,需要在以后的工作中进一步研究。
图8 绘制了地震响应沿楼层高度的分布,这有助于观察地震响应在各层之间的离散性。图8中给出了结构在所有地震动下的结果,可以看到各条地震动对应的响应之间存在着显著的差异。因此,检验设计结果时仅将响应的均值与性能目标值进行对比。
图8(a)表明结构的θp有在第2 层~第3 层集中的倾向,这与推覆分析中观察到的现象较为一致。最大的θp出现在第2 层,约为1.55%,比性能目标高出约3%。层间变形集中的现象可以归咎为BRB的屈服后刚度较小,一旦某层的支撑屈服,等效地震力难以在其他层进一步传递,从而容易引起变形集中的现象,这和大量既有文献[33]中所观察到的结果一致。同时,这也说明该设计方法未能充分考虑BRB 的这一力学特性,需要在未来的工作中加以改进。
图8(b)是θr的结果,呈现出和θp类似的分布规律。整体来看,θr集中出现在第2 层~第4 层,最大的θr出现在第3 层,约为0.53%,比设计目标高出约6%。这说明θr的实际均值和性能目标吻合良好。
图8(c)是PFA 的结果,其最大值出现在底层,约为0.5g,与性能目标相比有较大的安全裕度,这与图7(c)所观察的现象一致。PFA 的结果表明:式(17)~式(19)并不能准确估计加速度响应的大小,也未能较好地预测加速度的分布模式。
8 结论
本文为BRB 结构提出了一种新的抗震性能化设计方法,并选取了一栋六层BRB 钢框架的基准模型进行演示和论证。该方法的关键步骤在于,基于等效SDOF 体系的分析结果,建立起地震响应与结构周期(T)和强度折减系数(R)之间的关系。本文得到的主要结论总结如下:
(1) 不同地震响应对T和R的变化具有不同的敏感性。具体来说,峰值位移随着T的变长和R的增大而增大;延性在T<0.5 s 的范围内随T的变短而急剧上升,在整个周期范围内都随着R的增大而增大;残余位移总体上随着T的变长而增大,但是对R的变化则表现出不确定性;峰值加速度随着T的变长和R的增大而稳定地降低。
(2) BRB 钢框架的抗震性能评估结果表明:本文提出的设计方法可以使结构有效的同时满足峰值层间位移角和残余层间位移角的性能目标,误差约为5%;与此同时,结构的峰值楼面加速度与性能目标之间有一定的安全裕度。因此,本文建立的抗震性能化设计方法可以较好地预测结构的位移要求,对加速度需求的预测则有待于改进。
(3) 由于BRB 的屈服后刚度较小,结构容易出现峰值层间位移角和残余层间位移角在某些层集中的不利现象,这值得在以后的工作中进一步研究;另外,本文仅研究了一幢六层结构,对于层数更多或者高度更高的结构,其潜在的高阶模态效应还需进一步检验。
(4) 本文提出的抗震设计方法假定结构的变形沿建筑高度是均匀的且以一阶振型为主;但是,当结构在部分地震动作用下产生严重塑性损伤甚至濒临倒塌时,该方法的适用性还需进一步考察,同时,结构的真实响应与设计目标之间的差距也需定量评估。
