基于博弈论组合赋权的TOPSIS电能质量综合评估

刘康康，杨 超，薛仰孝，杜刃刃

（1 贵州大学 电气工程学院，贵阳 550025；2 国网渭南供电公司，陕西 渭南 714000；3 贵州电网有限责任公司贵安供电局，贵阳 550000）

0 引言

现代电力系统中存在大量的非线性和冲击负荷，同时新能源发电的并网渗透率逐年增高，这对电网的安全运行、用户的用电体验有着巨大的影响，从而电能质量问题关乎电网的安全经济运行以及用户的生产生活，成为减少经济损失所必须考虑的关键点。实现对电能质量进行科学有效的综合评估，对目前电力市场改革背景下进行电能质量的全面考核、依质定价和电能质量管控模型研究具有重要意义。

在电能质量评估中常使用层次分析法，为提高权重的准确性，研究者对传统的层次分析法进行改进。文献［4］引入模糊数学领域的模糊隶属度，将各指标以同种量纲加以规范化，提高AHP构建判断矩阵的一致性。考虑电能质量各指标间的复杂性和非线性特点，文献［5］采用三标度法（重要、同等重要、不重要）对层次分析法进行改进，使得对传统AHP判断矩阵的一致性有显著提高。考虑指标间的关联性，文献［6］提出将网络层次分析法（ANP）中由AHP计算部分替换为最优最劣网络法（BWM）计算电能质量指标的主观权重，基本避免了一致性检验无法通过的情况。根据指标间存在差异性与关联性，文献［7］采用CRITIC赋权法求取各指标的权重，并在理想解法中使用相对距离替代贴近度，提高其实用性，实现了对电能质量的综合性评估。考虑到SVM参数设置对评估模型的影响较大，利用粒子群算法（PSO）易实现全局优化能力对数据进行优化，提出PSO-SVM的电能质量综合评估。针对现有的评估方法对电能质量监测系统所监测的海量数据缺乏挖掘，对长时间周期情况下电网电能质量的整体情况难以判断，文献［9］在模糊综合评估基础上，引入数据包络分析（data envelopment analysis，DEA），实现某变电站母线监测点一年的电能质量综合评估。针对监测数据存在缺失、异常、偏移等数据质量问题，文献［10］根据电能质量数据特点提出相应的数据修复方法，研究质量问题中数据质量的良好程度对电能质量综合评估结果的影响，但研究中使用每天监测数据的95%概率值进行评估，这只能对应于大部分情况，如此只能对全年的电能质量进行大致评估，其中的少量数据尚未进行分析，这是否会对全年的电能质量有影响，也亟待更进一步的探讨与评判。

基于上述研究论述，本文提出基于博弈论组合赋权的TOPSIS电能质量综合评估方法。通过引入三标法对传统AHP进行改进，构建一致性矩阵提高一致性；其次，利用博弈论思想将主客观权重进行组合，使得最终权重合乎实际；最后，通过改进的TOPSIS模型进行电能质量的综合评估，并经算例验证了方法的可行性。

1 电能质量评价指标

图1 电能质量评估指标体系Fig.1 Index system of power quality evaluation

2 权重的确定

2.1 改进层次分析

层次分析法（AHP）是在进行主观赋权时常用的一种数学方法，但传统AHP构建的判断矩阵往往需要对一致性进行检验。由于受主观意见的干扰导致在构建判断矩阵时往往达不到工程实际的需要，得加以多次的调整。为了提高判断矩阵的一致性，引入三标法对传统的AHP进行改进。其流程如下：

（1）引入最优矩阵。利用三标法（-101）构建判断矩阵（a），其中矩阵（a）元素a含义如下：

根据专家意见得到各个评价指标的重要程度，得到判断矩阵（a），显然是主对角线为0的一个实数矩阵，若满足a＝-a，矩阵则为反对称矩阵。

如果反对称矩阵元素满足a＝a＋a，那么矩阵有传递性。当传递矩阵与矩阵满足下式：

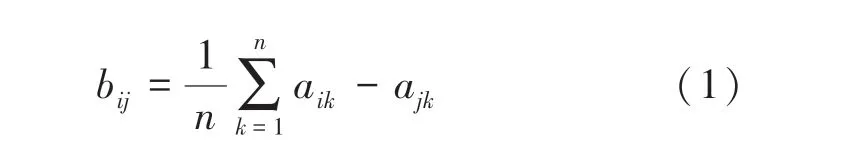
此时，矩阵称为的最优矩阵。

（2）引入一致性矩阵。当为最优矩阵且满足＝e，则矩阵是的一致性矩阵。的数学定义可写为如下形式：

（3）求取矩阵的最大特征向量，并对其进行归一化处理，最终结果为指标的主观权重｀。

2.2 博弈论组合赋权法

利用熵权法确定各评价指标的客观权重。在评价过程中，确定指标的权重时，单独使用主观赋权法，导致得到的权重主观性太强，受到决策者的个人意愿影响，缺乏客观性；而使用客观赋权法可以充分挖掘数据，但不会体现专家对各指标的重视程度。因此使用组合赋权法来确定指标的权重，使之包含主、客观因素，从而更加真实有效。本文采用博弈论思想将主、客观权重进行组合，得到指标的最终权重。其过程如下：

（1）将使用改进AHP得到的权重和熵权法得到权重，进行线性组合求取组合权重，表达式如下：

其中，，分别表示主观权重和客观权重的线性系数。

（2）利用博弈论思想求取权重纳什均衡点，即：

（3）对式（4）进行一阶求导，其最优解即是主、客观权重利用博弈论思想得到的最优权重组合，导数条件如下：

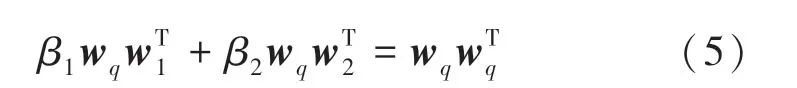
（4）根据式（5）求得权重系数，，并对其按下式进行归一化处理：

（5）确定最终组合权重，其值可由如下数学公式求出：

3 TOPSIS模型的电能质量综合评估

TOPSIS是一种通过计算各评价对象的指标数据与理想指标数据的欧式距离对评价对象进行优劣排序的综合评价方法。为消除评价指标间可能存在一定的线性关联，本文对传统的TOPSIS做出改进。现给出基本步骤分述如下：

（1）设评估对象为，评估指标为，为电能质量等级。将评估数据和标准数据组合得到样本矩阵，即（x）。这里在矩阵中，第1行是电能质量指标的等级样本，第（1）（）行是评估对象测量样本。

（2）数据归一化处理。本文所选取的指标皆为逆向指标，采用下式进行数据处理：

（3）构建加权样本矩阵（y），此处需用到的数学公式为：

其中。w为组合权重。

（4）确定正理想解A和负理想解A，利用夹角余弦分别求解第个待评价方案到理想解的距离。研究中推得的数学公式可分别表示为：

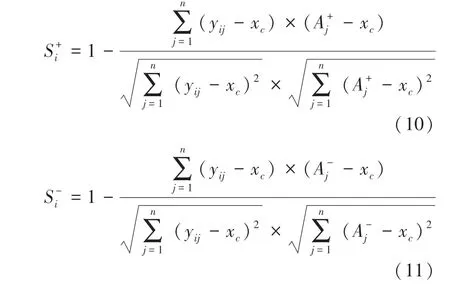
（5）计算各待评价对象的相对接近度C，数学定义公式见如下：

计算C值得到样本数据的优劣次序，结果值越大，表明其质量越接近正理想方案，即质量越好。本文基于博弈论组合赋权的TOPSIS电能质量综合评估流程如图2所示。

图2 基于博弈论组合赋权的TOPSIS电能质量评估Fig.2 TOPSIS power quality evaluation based on combination weighting of game theory

4 实例验证

本文选取0.38 kV线路的5个不同的观测点所采集的实测数据作为实例验证数据，实测数据见表1。根据专家意见，结合三标度法得到判断矩阵：

根据公式（1）求得的最优矩阵为：

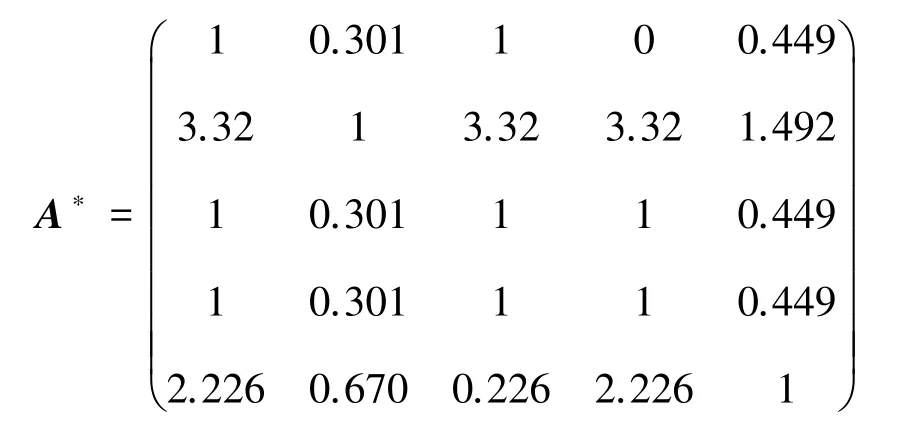
根据关系式＝e求得的一致性矩阵为：由于一致性矩阵具有一致性要求，不需要再次进行验证，直接求取其最大的特征向量，并进行归一化，得到的结果即为指标的主观权重：

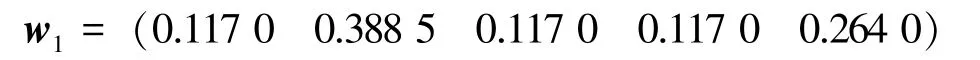
利用熵权法对实测数据处理得到评估指标的客观权重：

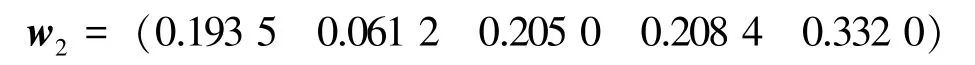
将、代入公式（3）可以解得：

根据公式（4）～（7）可以得到评估指标的组合权重：

将指标的实测数据与国际标准构建样本矩阵，根据公式（8）（9）建立样本加权矩阵：

根据公式（10）～（12）得到各个监测点与理想解间的贴近度，即：

由表1的计算结果得到5个监测点的电能质量优劣次序为：点1、点3、点4、点5、点2。文献［12］采用遗传投影寻踪插值模型对电能质量进行综合评估，5个监测点的电能质量优劣排序与本文一致，实例结果验证了本文方法的可行性。

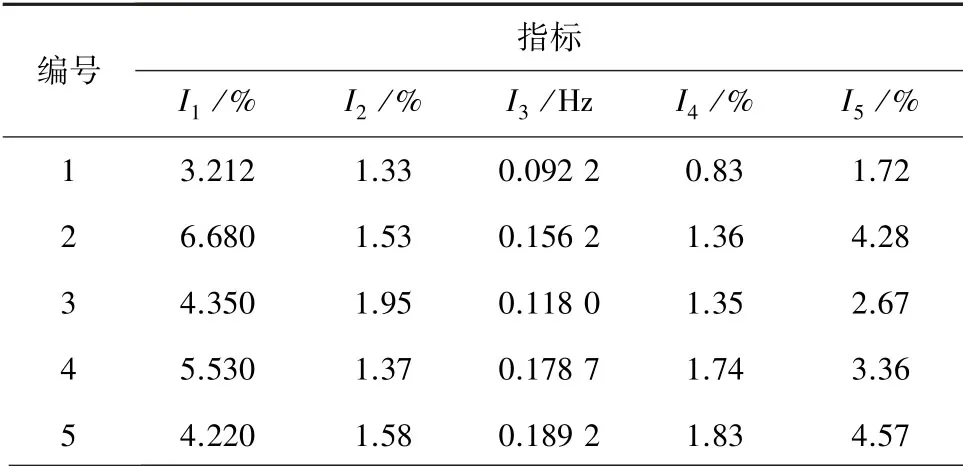
表1 实测数据Tab.1 Measurement data

5 结束语

针对运用AHP确定主观权重需要进行一致性检验，为提高一致性引入三标法对AHP进行改进，通过构建一致性矩阵提高一致性，使得主观权重更加实际。研究中，采用博弈论思想将主、客观权重进行组合，再使用改进的TOPSIS模型进行最终的评估，使得组合权重更加合理。因此本文提出基于博弈论组合赋权的TOPSIS电能质量综合评估法。算例结果表明本文提出的方法是一种可行的电能质量综合评估方法。