基于沥青混合料均匀性分析的有限元劈裂(IDT)仿真研究
2022-11-05吕悦晶张沪生程军勤
吕悦晶,张沪生,汤 文,樊 宇,程军勤
(1 武汉科技大学 汽车与交通工程学院,武汉 430065;2 青海省公路局,西宁 810001;3 青海省交通规划设计研究院有限公司,西宁 810001)
0 引言
沥青混合料均匀性直接影响沥青路面的的力学性能和使用寿命,同时也是导致沥青路面早期损坏的主要因素之一。
目前,国内外学者针对沥青混合料均匀性评价的研究已经取得了大量的成果。彭勇等人一直致力于从集料均匀性角度研究沥青混合料均匀性的量化表征问题,通过考虑二维截面上集料的分布数量、分布位置、面积比和转动惯量等方面提出了相关均匀性评价指标。郭乃胜等人采用CT识别技术,识别混合料试件内部结构,并以粗集料、沥青胶浆和空隙各组分的密度和面积为主要特征参数,建立了沥青混合料单一截面和单一试件的均匀性评价方法。李雪莲等人采用等面积环形分割法评价了就地热再生沥青混合料的均匀性。
然而,到目前为止国内外学者对于均匀性与力学性能之间关系的研究仍然处于探索阶段,且常规的试验方法很难用来研究二者之间的联系。因此,本次研究从细观结构出发,以沥青混合料粗集料(>2.36 mm)为主要特征参数,建立了一种沥青混合料均匀性评价指标。然后在此基础上,开展沥青混合料虚拟IDT试验数值模拟,通过加载不同方向的沥青混合料截面来模拟沥青混合料均匀性对IDT试验的影响,同时结合沥青混合料截面均匀性评价指标,建立沥青混合料均匀性与沥青混合料低温抗裂性能之间的联系。
1 混合料试件制备及图像处理
1.1 试件制备
本文采用马歇尔试验设计方法,根据《公路沥青路面施工技术规范》(JTG F40-2004)推荐的级配范围进行沥青混合料配合比设计,制作了2种级配类型的芯样(AC-13和AC-16)。制成试件之后在相同的CT设备参数下扫描沥青混合料试件,得到图像精度为1024×1024的扫描图,沥青混合料级配组成见表1。

表1 不同级配沥青混合料的级配曲线Tab.1 Gradation curve of asphalt mixture with different gradation
1.2 图像处理
为了更好地提取粗集料信息,需要对原始图像进行处理。对获取CT图像进行特征分析发现图像质量主要受亮度和噪声的影响。本文采用降噪+灰度均衡+分水岭分割的策略提取粗集料信息。图像处理过程如图1所示。
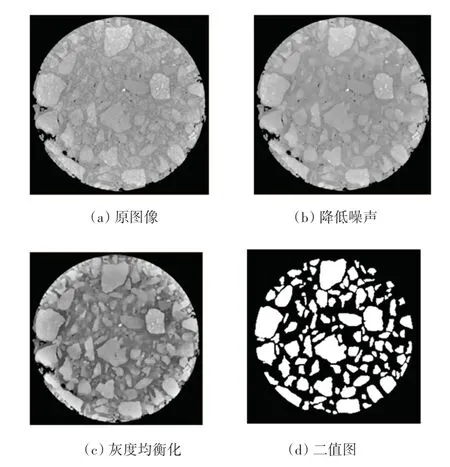
图1 图像处理示意图Fig.1 Schematic diagram of images processing
2 截面均匀性评价方法及指标
在沥青混合料均匀性研究中,粗集料的分布状态决定了其他组成成分的分布状态。因此,本文在获取CT图像粗集料信息后,以最邻近指数理论和沥青混合料颗粒分级理论为基础,建立了一种沥青混合料均匀性评价方法。
2.1 相邻集料位置分布
在沥青混合料均匀性研究中,不同粒径的集料颗粒在混合料中发挥的作用并不相同,因此在研究相邻集料位置分布前对沥青混合料中的颗粒进行分级。根据邢超研究结果,本文将粗集料分为2种类型:较粗的部分为主骨架颗粒,较细的部分为干涉颗粒,颗粒之间的粒径划分见表2。
由表2可知,AC-13和AC-16的颗粒分级临界筛孔都是4.75 mm,因此,以上文图像处理后得到的沥青混合料CT二值化图为基础,以4.75 mm作为临界值进行颗粒分级,分别得到主骨架颗粒图和干涉颗粒图,颗粒分级结果如图2所示。

表2 粒径分级范围划分表 Tab.2 Classification of particles size classification range mm

图2 颗粒分级示意图Fig.2 Schematic diagram of particles classification
最邻近指数理论是通过测度最邻近点的距离分析点的空间模式的一种常用的方法。具体定义如下:对于面积大小为的区域内随机分布点集,计算点集中任意一点与其最邻近点的距离,取这些最邻近距离的均值作为评价区域内点模式分布的指标,进而计算最邻近指数、即实际观测模式和完全随机模式(CSR)之间的比值来分析点的分布,该值可由如下公式计算得出:
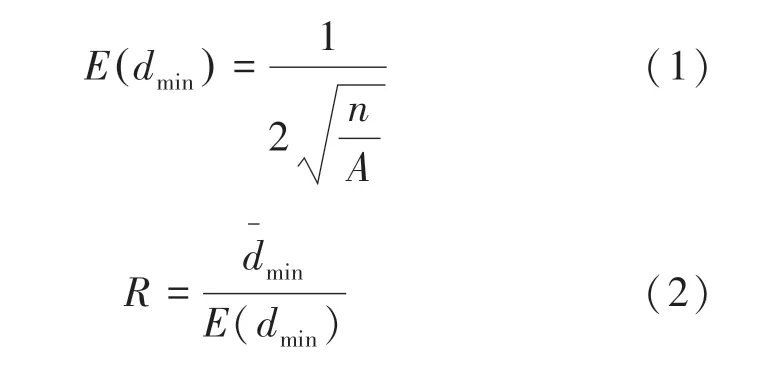
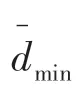
根据最邻近指数,可对点模式进行推断,依据如下:
(1)若1,点模式来自于CSR,属于随机分布。
(2)若1,点模式不来自于CSR,随机点在空间上相互接近,属于空间聚集模式,值越小,则越聚集。
(3)若1,点模式不来自于CSR,由于点之间的最邻近距离大于CSR过程的最邻近距离,空间点是相互排斥地,趋向于均匀分布,且值越大,越均匀。
各级颗粒相邻位置分布通过该级颗粒的加权最邻近指数来衡量。即以粗集料的质心点作为不规则随机点集,考虑集料大小因素,运用最邻近指数理论对粗集料的规则量化,建立离散点之间的联系。此处需用到的系列公式为:

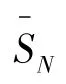
2.2 各级颗粒总质心分布
沥青混合料截面各级颗粒总质心分布状态通过该级粗集料的质心与截面几何中心的距离偏差率来衡量。公式为:
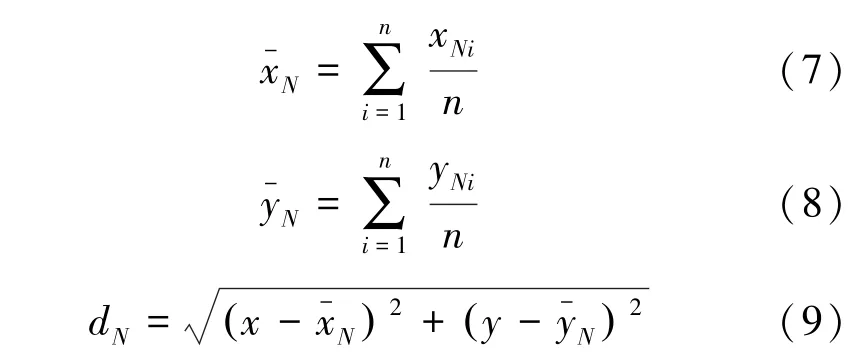
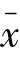
为了除去量纲的影响,将距离偏差d转化为量纲为1的距离偏差率r。公式为:

其中,表示截面几何中心至截面边缘的距离;r表示截面上第级颗粒集料质心与截面几何中心偏差率。
2.3 沥青混合料单截面均匀性评价及指标
提出U作为评价截面均匀性的指标,其定义如下:
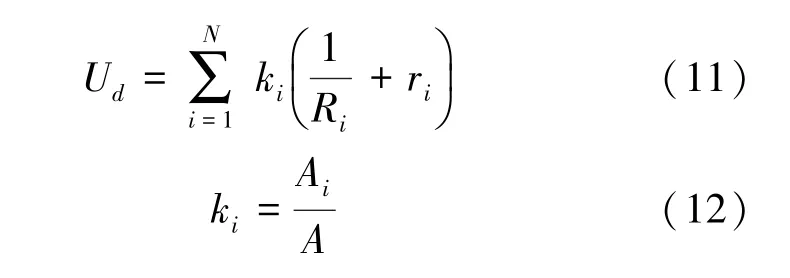
其中,U表示沥青混合料单一截面均匀性评价指标;k表示沥青混合料截面第级颗粒粗集料颗粒面积比;A表示沥青混合料截面第级颗粒粗集料总面积;表示沥青混合料截面内所有粗集料面积总和;R表示沥青混合料截面第级粗集料分布加权最邻近指数;r表示沥青混合料截面第级粗集料质心与截面几何中心偏差率。U值越小,则沥青混合料截面越均匀。
3 IDT试验有限元模型的建立
自编程序提取集料颗粒边界坐标信息,实现与有限元软件接口互通,采用三角形自由网格划分,设定沥青网格等级为6,集料网格等级为9。加载方式采用位移加载,加载速率为50 mm/min,底部约束,实验温度-10℃。底部通过encastre边界条件在每个自由度上固定。
文中采用广义Max-well模型,并根据文献[7]中在-10℃下的动态模量试验结果推导Prony级数系数,详见表3。
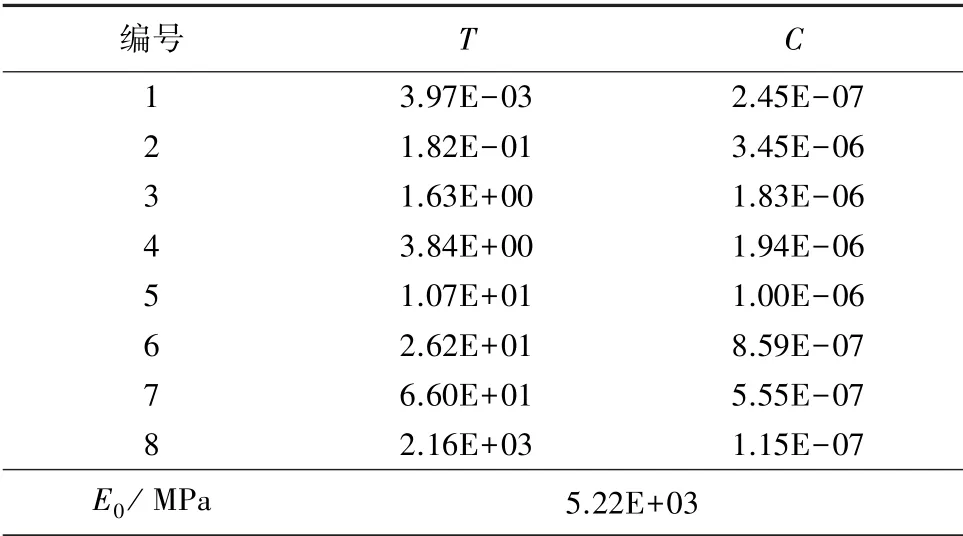
表3 广义Maxwell模型的Prony级数系数Tab.3 Prony series coefficients of generalized Maxwell model
假定沥青砂浆以及砂浆与集料之间的界面发生断裂,断裂在法线方向和切向方向相同。断裂能由Ding等人在不同温度下三点弯曲试验的基础上确定。将沥青砂浆-集料界面的抗拉强度设置为低于整体抗拉强度,-10℃温度下CZM模型参数见表4。
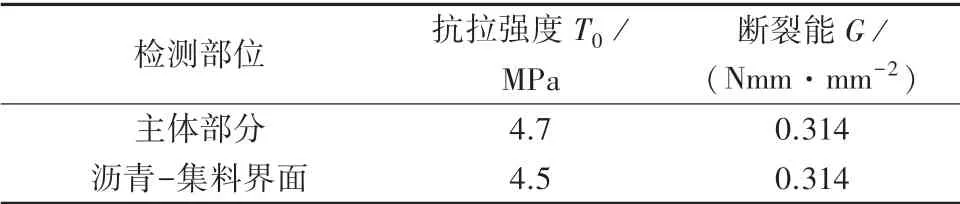
表4 不同温度下CZM模型参数Tab.4 CZM model parameters at different temperatures
为验证模型的合理性,通过仿真劈裂实验与室内劈裂实验进行比较。底部约束,顶部加载,加载速度50 mm/min,实验温度-10℃,采用8组细观模型进行劈裂试验仿真模拟,计算分析得到实验的最大反力平均值,并与文献[8]的实际劈裂实验结果进行了比较,如图3所示。对比结果表明该模型能够较好地模拟-10℃温度下沥青混合料的断裂行为。
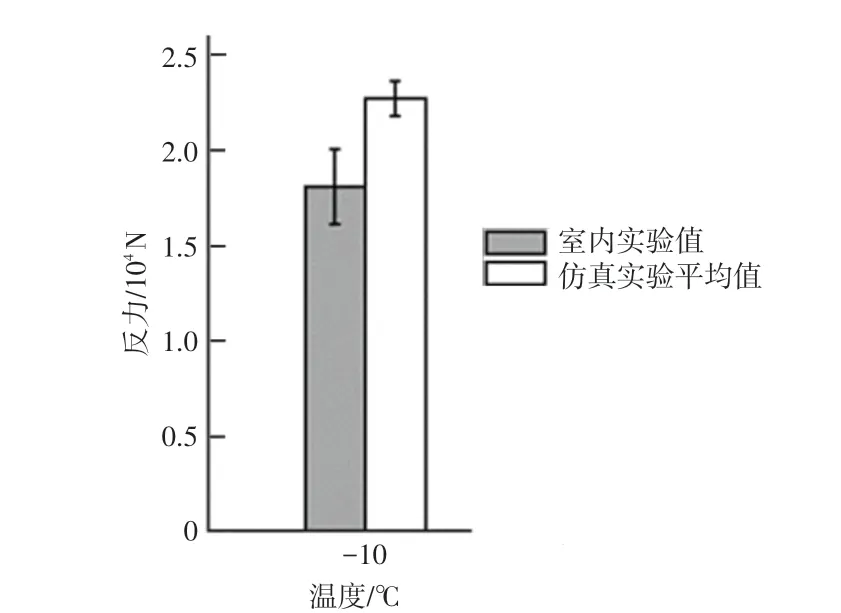
图3 -10℃下模拟和实验室劈裂实验的最大反作用力Fig.3 Maximum reaction force of simulation and laboratory splitting test at-10℃
4 沥青混合料均匀性对劈裂试验的影响分析
沥青混合料为非均质、各向异性的颗粒复合材料,劈裂试验中不同的加载方向影响到试件内部结构特征间的力学响应。为研究沥青混合料均匀性对劈裂性能的影响机理,本文对成型的AC-13、AC-16沥青混合料标准马歇尔试件进行断层扫描,间隔0.1 mm,剔除上、下部分的无效截面,保留320张CT断面图。由于断面图像数量众多,以同一间距分别在2组试件中选取8张典型截面进行后续研究,并根据定义,采用Matlab软件自编程序计算所取CT图像的沥青混合料截面均匀性指标,见表5。

表5 -10℃下IDT试验中劈裂强度的模拟结果Tab.5 Simulation results of splitting strength in IDT test at-10℃
采用Ansys软件,自编程序对沥青试件二维截面进行不同方向加载,相同骨料分布的不同试件分别用试件断面水平夹角0°、30°、60°、90°、120°、150°模拟代替。采用劈裂强度RT作为宏观力学指标并与截面均匀性指标进行对比分析,其中加载示意图如图4所示。
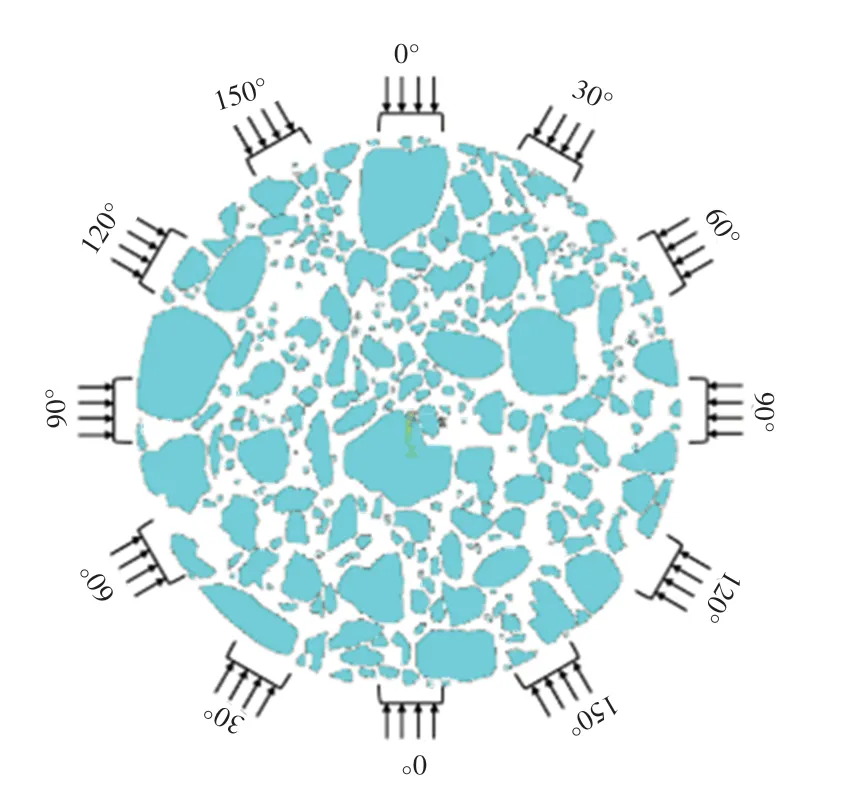
图4 不同加载方向与分析点位示意图Fig.4 Schematic diagram of different loading directions and analysis points
按照上述步骤运行后,水平截面各次旋转之后的反力-时间曲线如图5所示(以图1展示的截面为例)。
由图5反力-时间曲线发现,不同加载方向对沥青混合料劈裂试验有一定程度的影响,但总体来说曲线之间的行为又具有相似性,且模拟得到的曲线与实际实验记录的曲线接近。
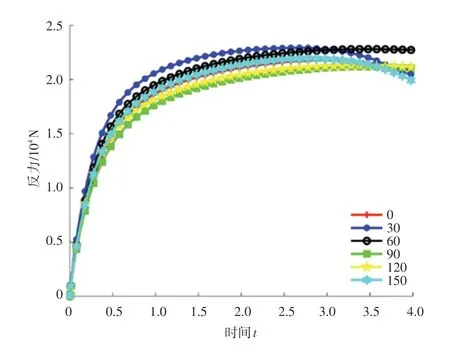
图5 劈裂试验力-时间曲线Fig.5 Force-time curve of splitting test
由表5中劈裂试验数值模拟结果与截面均匀性指标分析后可以发现:
(1)劈裂强度的变异性系数与均匀性评价指标间具有较好的一致性。
以劈裂强度变异性系数为纵坐标,以均匀性指标为横坐标画散点图,对其进行回归,如图6所示。
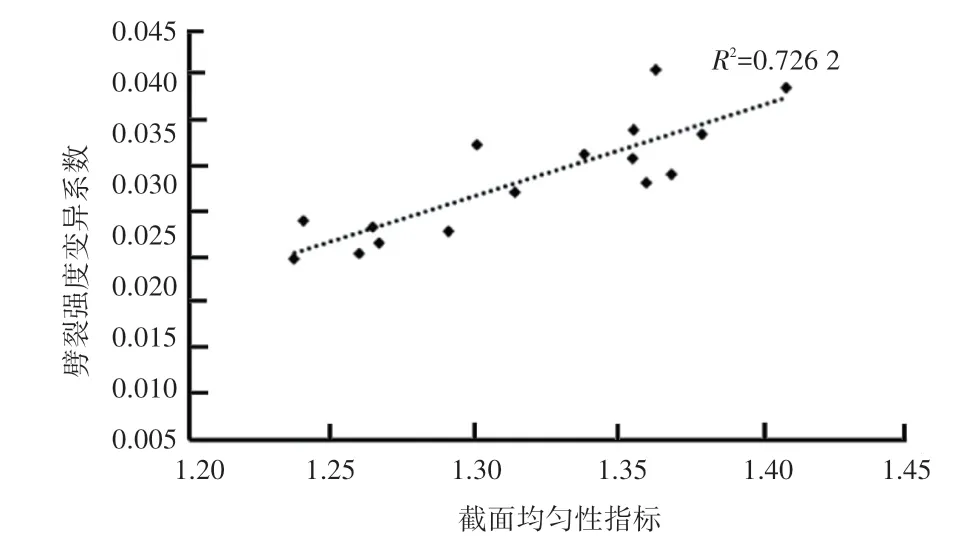
图6 劈裂强度变异系数与均匀性指标回归图Fig.6 Regression diagram of variation coefficients of splitting strength and uniformity index
结合表5和图6知,劈裂强度变异系数和均匀性指标之间在总体趋势上呈现为劈裂强度变异系数越大,均匀性评价指标U越大。即在总体趋势上,沥青混合料截面均匀性越好,对应的劈裂强度变化越小;而截面均匀性越差,劈裂强度的变化越大。但并不是严格意义上的一致,也会存在劈裂强度变异系数较大,而均匀性评价指标较小的情况。例如AC-13试件中截面1和截面2,截面1的均匀性指标为1.3134,相较于截面2的均匀性指标1.3004更大,均匀性更差,但是截面劈裂强度的变异系数却小于截面2。沥青混合料均匀性并不是影响劈裂强度变异系数的唯一因素,集料的形状、大小以及级配组成都影响劈裂强度的变异系数大小。
以所取截面均匀性评价指标的均值代替试件整体均匀性,结果见表6。

表6 沥青混合料试件整体均匀性指标Tab.6 Overall uniformity index of asphalt mixture specimen
同时,以8组截面计算所得的劈裂强度变异系数均值代替沥青混合料试件整体劈裂强度变异系数,如图7所示。
由表6和图7可知,AC-13试件的均匀性整体上要优于AC-16,同时,AC-13试件整体劈裂强度在变异系数上也小于AC-16。
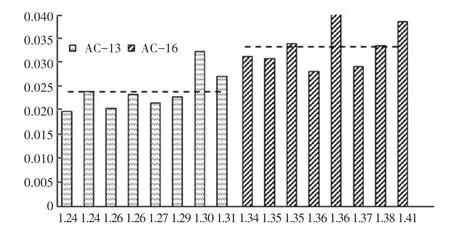
图7 各级配均匀性指标与劈裂强度变异系数直方图Fig.7 Histogram of distribution uniformity index and splitting strength variation coefficients at all levels
5 结束语
(1)基于CT扫描及数字图像处理技术建立了一种沥青混合料二维截面均匀性评价方法,提出了二维截面均匀性评价指标U。
(2)自编程序构建了二维沥青混合料有限元模型,并验证有限元方法的准确性和合理性。
(3)沥青混合料均匀性指标与劈裂强度变异性系数之间相关性显著。均匀性越好,劈裂强度变异系数越小;均匀性越差,劈裂强度变异性系数越大。为进一步研究均匀性与力学性能之间关系,提供了有益参考。
