垂直泊车路径跟踪控制研究

徐远征，吴长水

（上海工程技术大学 机械与汽车工程学院，上海 201620）

0 引言

城市停车位紧张、车位空间往往较小，泊车时所造成的剐蹭事故则不可避免地会时有发生。为提高泊车过程的安全性，自动泊车系统已成为了当前车企及研究机构的研究重点。一套完整的自动泊车系统可分为感知、规划以及运动控制三部分，而运动控制的好坏将直接决定最终的泊车效果及成功率，因此对其展开研究就有着较高的应用价值。通常来说，运动控制主要分为2部分：纵向控制以及横向控制。其中，纵向控制主要为针对车速的控制，稳定的车速对于泊车过程至关重要。横向控制则主要通过方向盘控制车身的横向运动，其控制精度将对路径跟踪效果产生较大影响。

目前，已有多位学者对自动泊车运动控制算法进行了研究。张家旭等人针对水平泊车，设计了一种基于滑模控制的泊车路径跟踪控制方法，仿真结果证明了所提出方法相较于传统的PID控制方法具有更好的抗干扰性及控制精度。黄晓峰综合考虑泊车过程中的各性能指标，分别采用前馈加反馈控制以及模糊控制方式，对方向盘转角和车速进行跟踪控制，在确保泊车控制稳定的基础上保证了一定程度的舒适性。Petrov等人则就泊车过程中转角连续抖动问题，针对不同的泊车工况，提出了一种基于饱和控制反馈的泊车控制方法，并通过仿真验证了所提出方法的可行性。

本文以垂直泊车为研究对象，提出了一种基于模糊PID和 模型预测控制（Model Predict Control，MPC）算法的车辆联合控制跟踪算法，并通过Simulink与Carsim进行联合仿真，验证了所提出算法的有效性。

1 泊车运动学模型及路径规划

1.1 车辆运动学建模

自动泊车运动过程中车速较低，此时可以忽略轮胎的侧向滑移，整个车身结构可视为刚体，因此本文将车辆简化为矩形，选用车辆运动学模型进行建模。车辆运动学模型如图1所示。

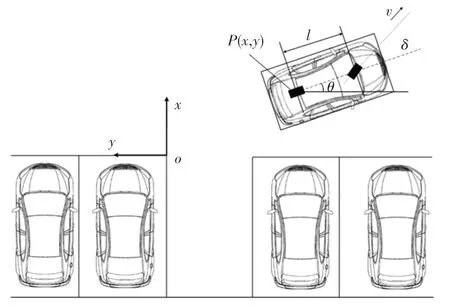
图1 车辆运动学模型Fig.1 Vehicles kinematics model

由图1可知，本文以垂直车位左上角点为原点建立全局坐标系，此时车辆位置坐标由车辆后轴中心在全局坐标系下的坐标（，）确定，车身的角度由车辆在全局坐标系下的航向角确定。本文建立的车辆运动学模型如式（1）所示：

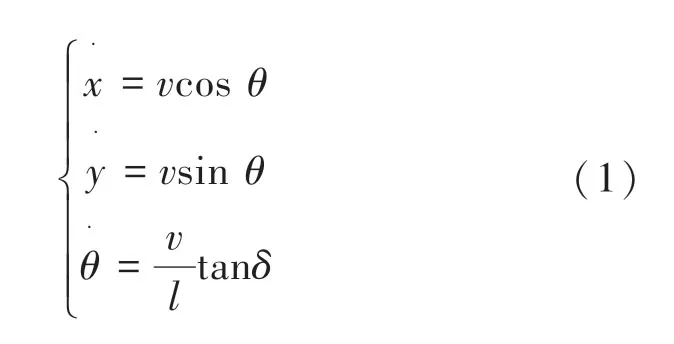
其中，为车速；为轴距；为车辆前轮等效转向角。研究可知只需输入车辆速度及前轮的等效转向角，便可求得当前车辆在全局坐标系下的位姿（，，）。

1.2 垂直泊车路径规划

本文使用快速探索随机树（Rapidly-exploring Randomized Tree，RRT）算法进行垂直泊车路径规划，RRT算法是一种使用增长树的搜索算法，其优势在于无需对泊车空间进行几何划分，算法灵活性较高。RRT算法伪代码详见如下。

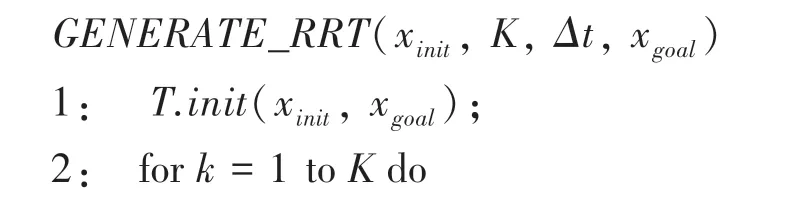
路径规划的具体步骤为：

（1）根据起始点x、目标点x、循环次数、拓展步长以及环境等变量初始化各项参数。

（2）在环境中生成随机采样点x，然后遍历树上已有的节点，通过_函数选择离其最近的树节点作为扩展节点x。

（3）通过拓展函数_生成新节点x，并将其索引、边界添加到树中。

（4）判断树是否拓展到距离x的某一范围内，若是，则结束拓展、并输出路径，否则进行下一轮循环。

路径规划结束后，往往由于路径不够平滑，无法满足车辆运动学约束。本文使用（）曲线进行路径优化。曲线是在曲线上的一种改进、即假定车辆转向时始终按照最小转弯半径进行转向，且曲线中的各段路径均为圆弧及直线的组合。RRT路径优化过程如图2所示。优化方法为：从起始点开始，从小到大遍历RRT树上点的索引，若2个点间存在无碰撞的路径，则用曲线替换原有的路径，而后再以当前点为起始点进行新一轮的优化，直到优化结束。

图2 RRT路径优化Fig.2 RRT path optimization

2 基于模糊PID算法的车辆纵向控制

2.1 模糊PID算法架构

模糊PID控制算法将传统的PID控制算法和模糊算法相结合，可通过经验化的模糊规则实时调整PID算法的参数，以此弥补传统PID算法不适用于非线性系统的不足，本文设计的模糊PID算法框图如图3所示。由图3可知，模糊控制算法的输入为目标车速以及车辆模型返回的实际车速，输出为车辆模型所需的加速度。算法运行时，可循环比较目标车速与实际车速之间的的差值以及差值的变化率E，通过模糊控制算法求得K、K、K的补偿值更新PID控制器的参数，再由PID控制算法计算出期望加速度，进而控制车辆运动。

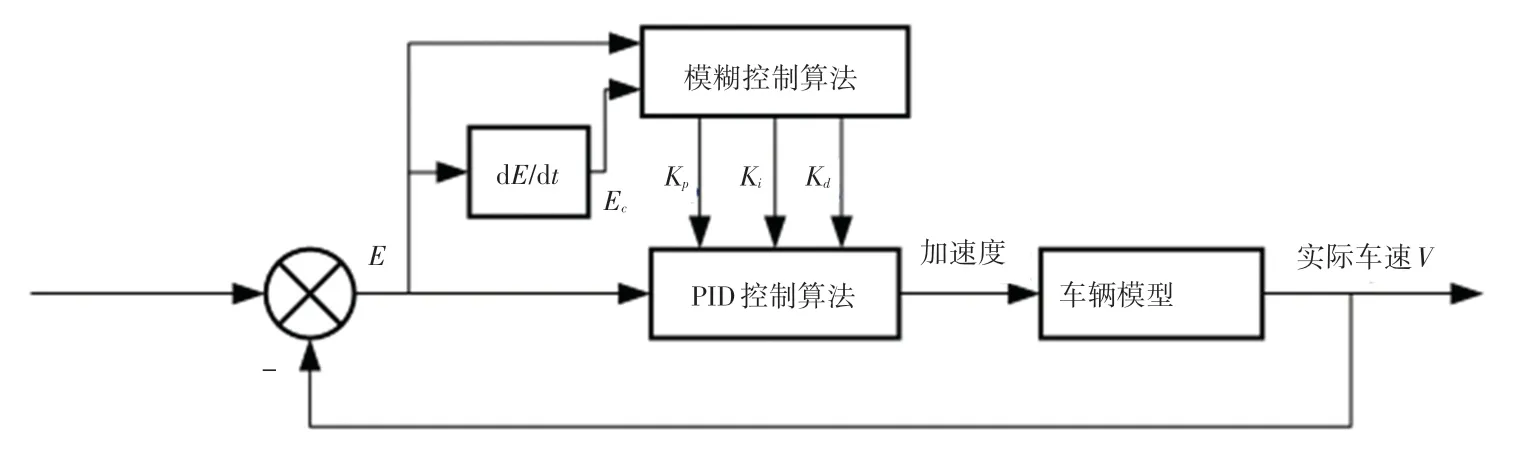
图3 模糊PID算法框图Fig.3 Block diagram of fuzzy PID algorithm

2.2 模糊控制算法

模糊控制器主要由模糊化、模糊推理以及清晰化三个模块组成，如图4所示。图4中，模糊化模块通过输入隶属度函数将清晰的论域转化为模糊集合；模糊推理模块是通过设定的模糊规则推理出输出变量的隶属度；清晰化模块则根据输出变量的隶属度函数及论域进行反模糊化，计算得到输出变量的精确值。

图4 模糊控制算法框图Fig.4 Block diagram of fuzzy control algorithm

2.3 模糊化

本文将各参数的模糊子集定义为：｛负大，负中，负小，零，正小，正中，正大｝，对应符号为｛NB，NM，NS，Z，PS，PM，PB｝。参考实际调试过程中各参数的实际变化范围，对于输入参数，本文设定输出值与参考值之间的误差值的论域为［-1，1］，误差值变化率E的论域为［15，15］。对于输出值，本文设定输出的K的论域为［03，03］，K的论域为［006，006］，K的论域为［3，3］。若上述参数的实际值超过变化范围，则取边界值进行计算。

常用的隶属度函数有：三角形函数、梯形函数、高斯分布函数等。参考文献［9］的方法以及实际调试效果，本文将各变量中间的隶属度函数设定为三角形函数，两侧的隶属度函数设定为高斯分布函数，如图5所示。

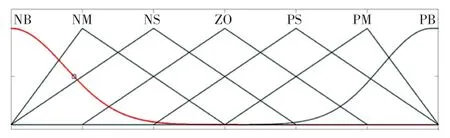
图5 各变量隶属度函数设置Fig.5 Membership function setting of each variable

2.4 清晰化

本文根据泊车过程的工程实践经验分别对K、K、K设置了相应的模糊规则表，根据误差及误差的变化率即可推理得到K、K、K的隶属度。

常用的清晰化方法有：最大隶属度法、重心法以及加权平均法，综合考虑计算复杂度以及实际控制效果，本文采用加权平均法进行清晰化。各个输出参数的输出曲面如图6所示。

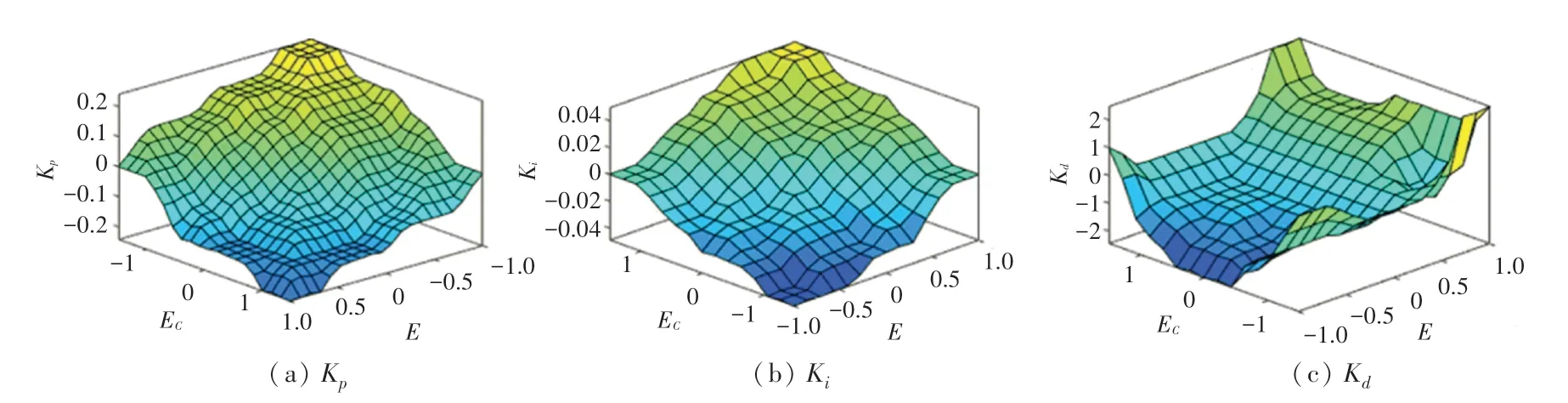
图6 输出参数曲面图Fig.6 Output parameters surface diagrams

3 基于MPC算法的车辆横向控制

3.1 MPC算法架构

模型预测控制算法通常可分为预测模型、滚动优化以及反馈校正三部分。本文根据垂直泊车的横向控制需求，设计得到的MPC算法架构如图7所示。图7中，输入为车辆当前的位姿以及车速，输出为目标车速以及方向盘转角的控制信号，其中目标车速作为模糊PID算法的参考值。

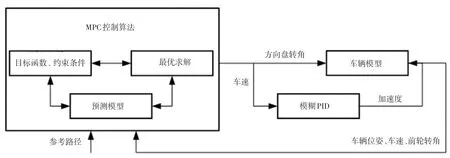
图7 MPC算法架构Fig.7 MPC algorithm architecture

3.2 预测模型

低速状态下轮胎滑移量可忽略，本文使用车辆低速运动学模型作为预测模型。由于上文建立的低速车辆运动学模型为非线性时变系统，无法确保控制系统的实时性，因此本文对其进行线性化处理。

在控制车辆横向运动时需跟踪车辆的实时位姿，本文选取系统的输入为（，），将系统的状态变量用（，，）表示。根据路径规划的任意参考点的参考状态χ（x，y，θ）以及对应的参考输入u（v，δ），推导可得到以为采样时间的离散化误差模型，推导得到的该模型的数学表述见式（2）：

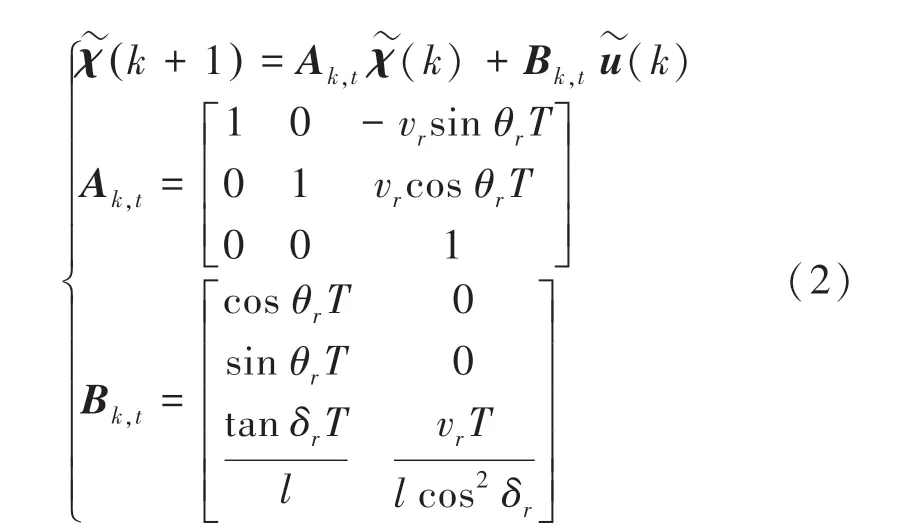
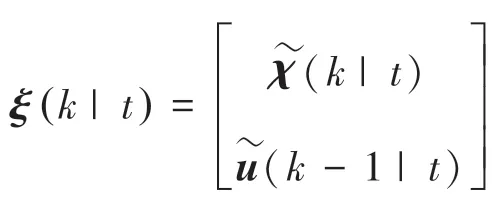
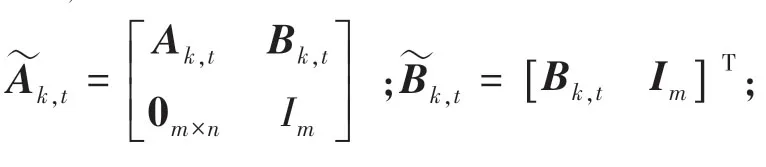
为提高模型效率，令A＝A，B＝B，得到的预测模型可根据时刻的系统状态以及N各时域的预测输入预测N各时域内的输出。此时推得的数学公式为：

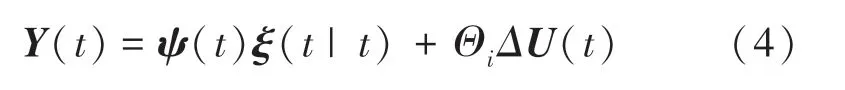
其中，

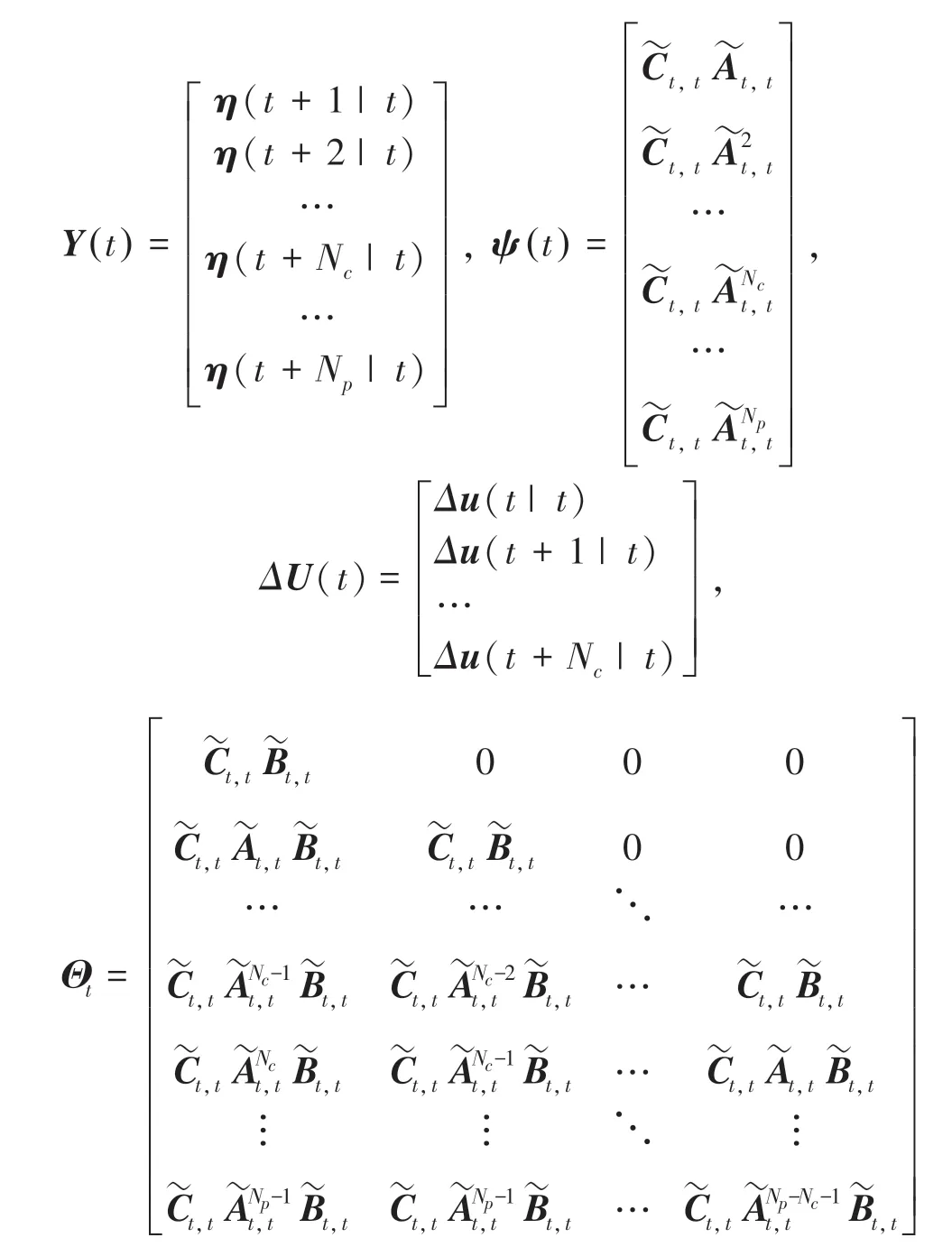
3.3 目标函数及约束条件

为使控制过程更为平稳，本文使用目标函数为：

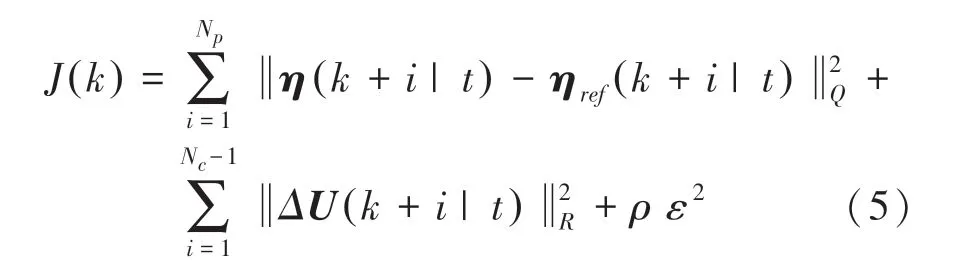
其中，N为预测步长；N为控制步长；为权重系数；为松弛因子；和分别为状态量和控制量的权重。

设定采样时间0.02 s，为了使泊车期间车辆速度及航向角变化平稳，本文设定的速度及前轮转角的控制量及控制增量约束如式（6）所示：

4 仿真验证

4.1 仿真参数设置

本文在Matlab／Simulink搭建相应的算法，并在Carsim中配置相应的车辆参数，实现Carsim与Simulink的联合仿真。本文搭建的仿真环境如图8所示，所用的仿真参数见表1。

图8 联合仿真模型Fig.8 Co-simulation model

表1 仿真参数Tab.1 Simulation parameters

4.2 实验结果分析

垂直泊车路径跟踪控制的整体效果如图9所示。图9中，实线部分为车辆实际运动轨迹。图10显示了车辆各执行器的相应情况。泊车开始后，车辆首先挂档，向右打方向盘行驶到点2，在此过程中车速缓慢上升。然后向左打方向盘行驶到点3，此时车速缓慢下降至0 km／h。之后车辆挂档，向右打方向盘开始倒车，行驶到点4后回正方向盘，并适时调整其角度，使车辆沿直线泊入车位至缓慢停止。最后回正方向盘，档位切换为档，泊车结束。

图9 规划路径与实际路径对比Fig.9 Comparison of planned path and actual path

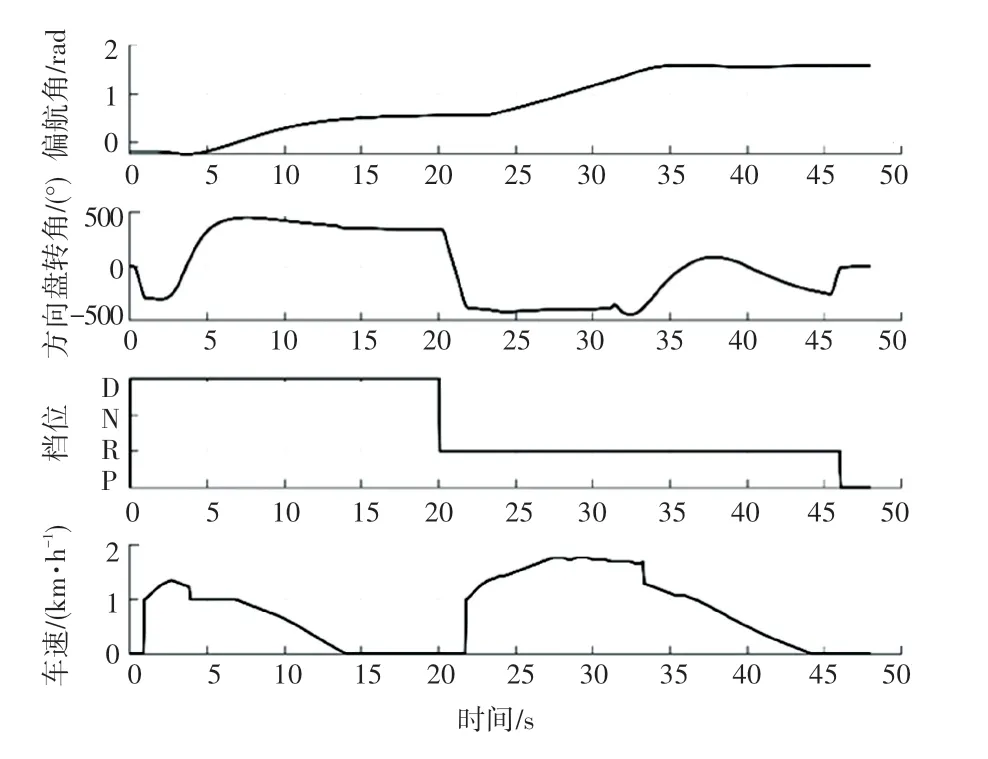
图10 执行器响应Fig.10 Actuators response

综上可知，实际路径与规划路径较为吻合且变化趋势一致，车辆最终的泊车位姿与目标位姿偏差不大，且在泊车过程中没有碰撞、压线等情况的发生。整个泊车过程中方向盘转角不超过450°，满足车辆转向约束。车辆车速变化较为平缓，车速控制在2 km／h以内，验证了模糊PID算法的有效性。故本文所提出的垂直泊车跟踪控制算法能够对规划的路径进行较好的跟踪，并控制车辆以较小的误差按照该路径泊入目标车位。

图11为规划车辆位姿与实际车辆位姿的误差。由图11可知，车辆实际的偏航角与路径规划的偏航角误差的绝对值控制在0.057 m以内，规划路径与实际路径的横向偏差的绝对值控制在0.08 m以内。分析图9可知，上述误差并不会使车辆与外界环境发生碰撞，考虑到Carsim车辆模型模拟了真实的泊车环境，在泊车过程中存在较多的环境干扰，上述误差范围区间较为合理。因此，本文建立的垂直泊车路径跟踪控制算法具有良好的跟踪控制效果。

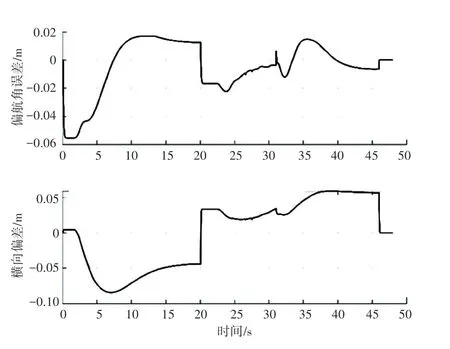
图11 偏航角、横向角误差Fig.11 Error of yaw angle and lateral angle

5 结束语

垂直泊车车位狭小，易造成剐蹭碰撞等危险情况的发生，往往对车辆控制精度具有较高的要求。本文以垂直泊车为研究对象，提出了一种基于模糊PID算法与模型预测控制算法的自动泊车联合控制算法。联合仿真结果表明：本文提出的跟踪控制算法精度较高，可以控制车辆在允许的误差范围内沿规划的路径行驶。此外，该方法对水平泊车、斜列泊车也都具有一定的参考价值。