基于MLP的上海市主要树种单木胸径生长率模型

肖舜祯，刘 强，徐志扬，刘龙龙，朱海伦

（国家林业和草原局华东调查规划院，浙江 杭州 310019）

【研究意义】单木胸径生长率模型是研究林分生长变化规律和预估林分生长量、收获量的基础手段，也是估测林木生物量、碳储量及其动态变化的主要工具，对于森林资源经营管理具有重要意义[1]。【前人研究进展】国内外学者们对单木胸径生长模型开展了很多应用研究，如Subedi 等[2]建立了黑云杉和短叶松人工林非线性混合效应生长模型；Bohora 等[3]使用分位数回归和混合效应模型预测树木生长；Ma 等[4]利用东北195 个样地连续观测数据建立蒙古天然栎林单株直径生长非线性模型预测林木生长和林分产量；Briseño-Reyes 等[5]利用样木实测数据建立30 个树种的单木胸径生长幂函数模型来预测墨西哥杜兰戈混交林生长；Huy等[6]考虑生态环境因子和气候因子采用加权混合效应模型对达拉特松的生长进行建模以预测林木生长；李春明[7]在选择合适异方差和自相关函数后采用两层次线性混合效应模型方法建立了江西省杉木人工林单木胸径生长模型；鲁乐乐等[8]采用贝叶斯模型平均法（BMA）和逐步回归法（SR）分析杉木单木胸径生长量与内部因子（林分变量因子）和气候因子的关系并构建了杉木单木胸径生长模型；张海平等[9]通过分析大、小兴安岭地区林分因子及气象因子的差异并采用哑变量方法构建了含区域效应的单木直径生长模型。此外，国家森林资源连续清查积累了大量单木胸径实测数据，部分研究人员利用该数据建立了区域范围的线性或非线性模型用以开展森林资源年度更新等，如陈国栋等[10]基于新疆天山70块清查固定样地考虑密度效应和样地效应建立了云杉单木胸径混合效应模型；段劼等[11]基于4期北京市侧柏人工林一类清查样地选用林木生长、立地条件和林木竞争3类因子建立了胸径生长模型；曾伟生等[12]利用第八次全国森林资源清查内蒙古自治区2013 年清查的12 万株保留木前后期实测胸径数据，分内蒙地方和内蒙森工2个建模总体，建立了各个树种的立木胸径生长率模型；马克西等[13]利用第八次全国森林资源清查青海省前后期实测样木数据，建立了4个主要树种组的立木胸径生长率模型；曾伟生等[14]基于全国第六次至第九次清查河北固定样地数据采用非线性回归建模方法建立了18个树种组的单木胸径生长率模型。然而，这些方法通常以一定的统计假设为前提，譬如数据的独立、正态分布以及等方差等，但是，森林生长数据具有连续观测和层次性等特点，这些假设条件通常情况下难以充分满足，有必要尝试新的方法[15-16]。

【本研究切入点】随着计算机技术发展，人工智能模型为克服这类问题提供了更为先进的技术思路。人工神经网络作为人工智能的一个分支，它对数据分布没有假设要求，能很好地处理非线性、非高斯分布和包含噪声的低质量数据。而且建模前不需要明确模型具体形式，非常适宜处理复杂的多变量、非线性问题，这已在树高曲线与各类储量预测方面有所应用[17-22]。然而，利用神经网络方法建立单木胸径生长率模型的研究，目前却鲜见报道。【拟解决的关键问题】长期以来上海市一直缺乏具有大量数据支撑且准确可靠的单木胸径生长模型。因此，尝试利用上海市4期固定样地数据，在单木水平上研究利用多层感知机和传统非线性回归模型建立和优选主要树种的胸径预测模型，以期为上海市森林资源年度更新提供依据。

1 材料与方法

1.1 数据来源与处理

1.1.1 数据来源采用第六次至第九次全国森林资源连续清查上海市1999、2004、2009、2014 年固定样地保留木前后期单木胸径数据，将保留木3期动态数据（1999—2004、2004—2009、2009—2014）进行合并生成单木样本。

1.1.2 数据处理将单木数据分为水杉（Metasequoia glyptostroboides）、樟树（Cinnamomum camphora）、女贞（Ligustrum lucidum）、木兰（Magnolia liliflora）、杨树（Populusspp.）5个树种，共9 752株保留木。再按以下方式进行处理：

（1）异常样木剔除。首先剔除胸径生长量等于0 以及负生长的样木；再分树种计算复位样木胸径生长量的平均数和标准差，以2倍标准差为临界值筛选剔除异常样木，并且按复利式计算年均胸径生长率，绘制散点图，剔除生长率明显过大的异常样木[14]。最后参与建模的数据为9 333 条记录，异常样木剔除比例为4.30%。

（2）数据合并。考虑到部分树种单木数据量过大（水杉、樟树建模数据量分别为4 320、3 553），且按径阶的分布极不均匀，故将各树种相同前期胸径（按0.1 cm）的单木数据进行分组处理，胸径生长量使用组内样木算术平均数，然后再计算相应的生长率[14]。各树种组样木株数及建模样本单元数见表1。

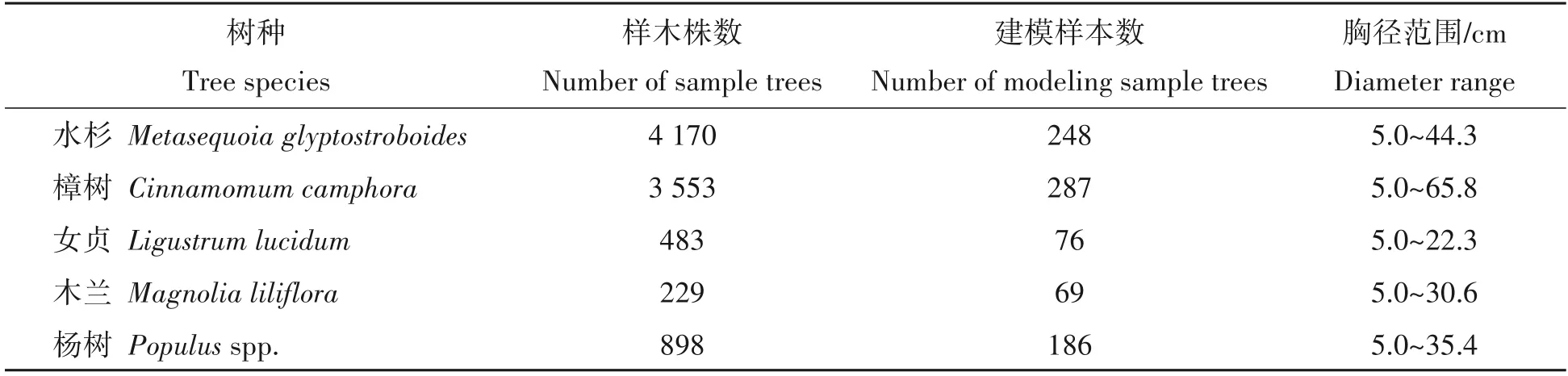
表1 建模数据基本情况Tab.1 General situation of modeling tree data

1.2 单木胸径生长率模型

1.2.1 传统非线性回归模型单木生长率传统非线性回归模型按一元模型表述如下[14]：

式（1）中：P为胸径生长率（%）；D为林木胸径（cm）；a，b为模型参数；ε为误差项，假设服从均值为零的正态分布。由于各树种组生长率数据的异方差性不显著（图1），参数估计采用非线性普通最小二乘法。

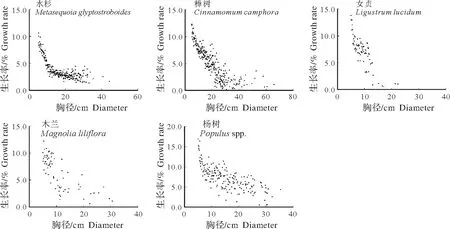
图1 上海市主要树种生长率与散点Fig.1 Scatter plot of growth rate and diameter for major tree species in Shanghai

1.2.2 人工神经网络模型多层感知机（multilayer perceptron，MLP）是一种全连接人工神经网络（artificial neural network，ANN），由输入层、至少1 个隐藏层和输出层组成，层间进行全连接，输入数据经过运算、激活函数激活后传输作为下一层输入，逐层向后运算至输出层，使用梯度下降改进模型参数使损失最小化，其函数逼近能力较强，对输入变量无统计上的分布要求，预测精度较高，应用广泛[20]。

基于Python3.6的PyTorch深度学习框架，分树种建立多层感知机人工神经网络模型以预测上海市主要树种单木胸径生长率。模型输入层为样木胸径，输出层为胸径生长率，均为1个单元，为探索隐藏层数量以及各隐藏层的合理单元数量，采用网格搜索的方法对隐藏层数（1、2）、隐藏层单元数（1～30）进行循环迭代训练，迭代最大轮次3 000次，观测模型的生长率损失值（LOSS）。为防止模型过拟合，采用提前终止策略，在连续100 次迭代损失值（LOSS）都无法下降时提前中止，同时记录下每次搜索时的隐藏层数、隐层单元数、迭代轮数以及模型权重参数等。经实验比较选择最优超参，本文损失函数采用均方误差，激活函数采用sigmoid函数，优化函数选用Adam算法。

1.3 模型评价

借鉴前人模型评价方法，采用两部分进行模型评价：一是对胸径生长率模型本身的评价，主要利用确定系数R2和估计值剩余标准差SEE；二是基于生长率模型用林木的前期胸径预估后期胸径的评价（相当于对模型D2=f（D1）评价），除了采用确定系数R2和估计值剩余标准差SEE 评价外，还采用平均预估误差（MPE）和平均百分标准误差（MPSE）进行综合评价[12-13]。公式如下：

2 结果与分析

2.1 传统非线性回归模型

采用式（1）对5个树种拟合单木胸径生长率模型，并计算建模样本的确定系数和估计值剩余标准差，结果如表2所示。

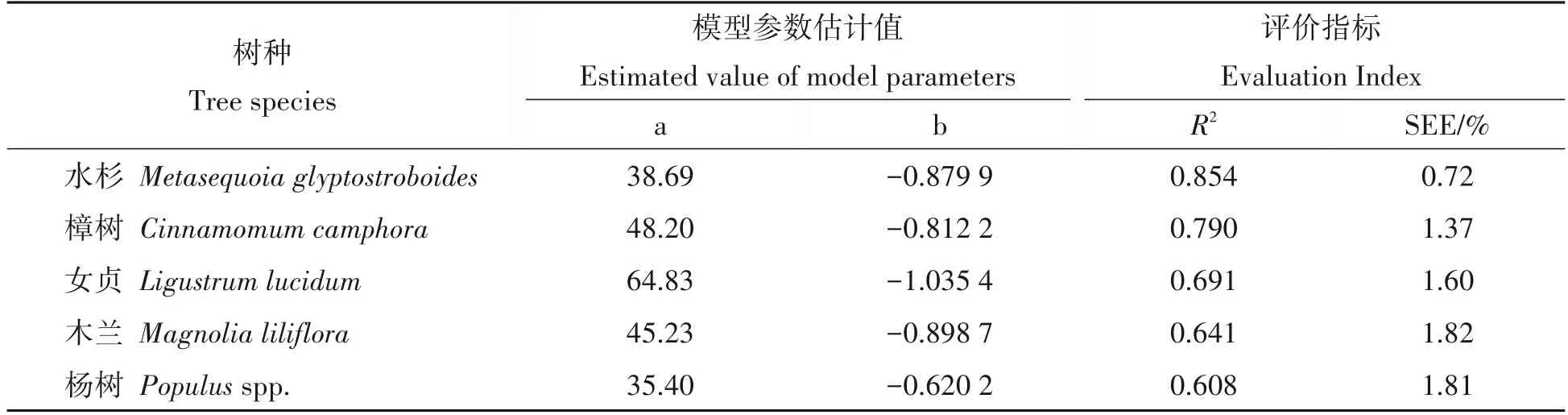
表2 单木胸径生长率非线性回归模型拟合结果Tab.2 Fitting results of diameter growth rate nonlinear regression models for individual trees

表2中模型评价的决定系数和剩余标准差仅针对单木胸径生长率，而胸径生长率模型则服务于单木胸径预测，因此，应以后期胸径作为目标变量，与预估值比较计算各树种组模型的预估评价指标。表3列出的结果是使用全部建模样本计算的4 项评价指标，可见除女贞确定系数为0.526 外，其余基本达到0.8以上，平均预估误差（MPE）都在2%以内，平均百分标准误差（MPSE）都在20%以内，表明该生长率传统非线性回归模型对上海市各树种胸径预测整体可靠。各树种的预测胸径残差分布如图2，均未表现出较为明显的异质性。

图2 单木胸径生长率非线性回归模型胸径预估残差Fig.2 Residual plot of diameter prediction based on individual tree diameter growth rate nonlinear regression models

表3 单木胸径生长率非线性回归模型胸径预估评价Tab.3 Evaluation of predicted diameter using individual tree diameter growth rate nonlinear regression models

2.2 多层感知机建模

通过建立多层感知机模型并经过循环迭代训练，确定各树种胸径生长率模型的隐藏层数为1时即可使模型最优，并确定隐层单元数、迭代轮数。用最优模型对建模样本进行生长率预测，计算确定系数和生长率估计值剩余标准差，结果如表4。从评价指标可以发现，与传统非线性回归模型相比，各建模树种的确定系数提升0.042～0.073，剩余标准差最多下降0.32个百分点（女贞）。从建模样本评价指标看，多层感知机模型略优于传统非线性回归模型。

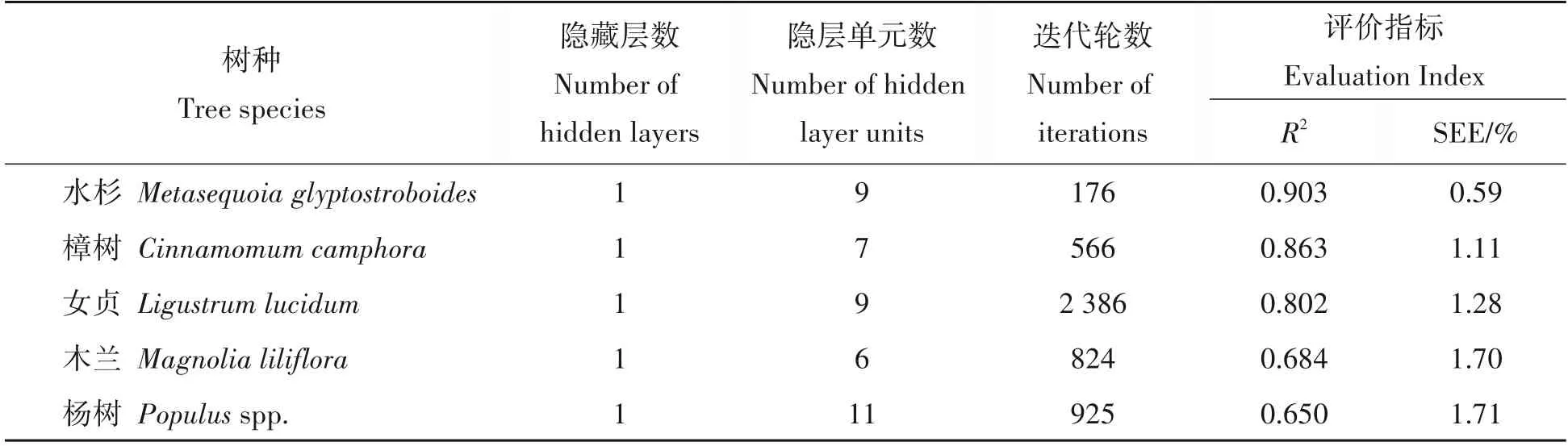
表4 单木胸径生长率多层感知机拟合结果Tab.4 Fitting results of diameter growth rate MLP models for individual trees

以全部样本的后期胸径作为目标变量，用所建多层感知机模型生成胸径、生长率序列，并对各树种的前期胸径进行生长预估，比较目标变量与预估值，计算4项评价指标，结果如表5所列。可见除女贞确定系数为0.561外，其余各树种确定系数均达到0.8以上，平均预估误差（MPE）都在2%以内，平均百分标准误差（MPSE）也在20%以内，验证了多层感知机生长率模型对上海市各树种胸径预测的可靠性。各树种的预测胸径残差分布如图3，亦均未表现出较为明显的异质性。

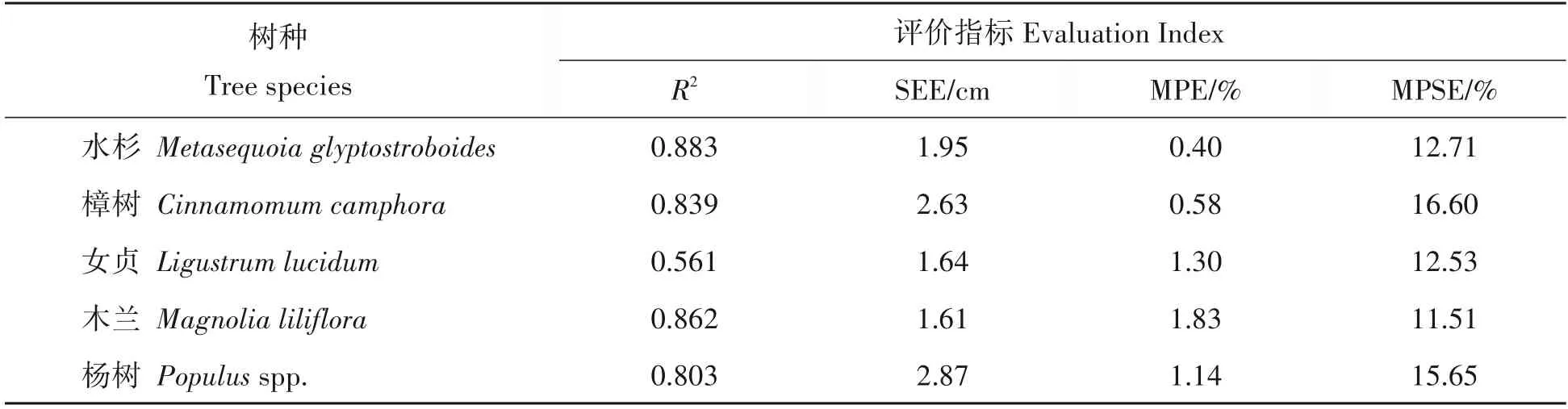
表5 单木胸径生长率多层感知机模型胸径预估评价Tab.5 Evaluation of predicted diameter using individual tree diameter growth rate MLP models

对比表3、表5可发现，在用全部样本对2种模型进行检验评价时，5个树种的评价指标均略优于异速生长方程，确定系数提升0.002～0.035；对比图2和图3的预测胸径残差图也可发现，5个树种的多层感知机模型残差散点图在不同程度上向零值线收敛得更好、预测效果要略优于异速生长方程。

图3 单木胸径生长率多层感知机胸径预估残差Fig.3 Residual plot of diameter prediction based on individual tree diameter growth rate MLP models

3 结论与讨论

本研究基于第六次至第九次全国森林资源连续清查上海市1999、2004、2009、2014 年固定样地保留木前后期单木胸径数据，采用传统非线性回归模型、多层感知机模型2 种方法分别建立了上海市5 个树种的单木胸径生长率模型。总体来看，多层感知机胸径生长率模型略优于非线性回归模型，5 个树种的多层感知机单木胸径生长率模型预估全部林木后期胸径时，除女贞确定系数为0.561 外，其余各树种确定系数均达到0.8 以上（0.803～0.883），较非线性模型分别提升0.003、0.007、0.035、0.002、0.004，平均预估误差（MPE）均在2%以内，相当于用这些模型更新胸径时能达到98%以上的预估精度。因此，更建议采用多层感知机单木胸径生长率模型为上海市森林资源年度监测数据更新提供参考。

但是，本文基于一类清查复位样木数据建立单木胸径生长率模型，由于样木数量有限和不同树种建模样本量差异较大，导致所建模型的预估结果精度与其他类似研究相比有一定差距[12-14]。如全部样木数仅9 333株，女贞、木兰仅483株和229株，这些对模型建立以及预估精度评价均产生一定影响。此外，由于上海市造林过程中多使用大苗造林，树木和样地的准确年龄信息尚有待考证，因此并未将年龄信息引入模型参数中。随着国家林草湿调查监测的工作推进，应不断积累样地调查数据，或者可以引入上海周边立地和气候条件相似地区的调查数据，对本文所建胸径生长率模型进行更新和修正以提高预估精度。