基于信息熵的调频引信分数域干扰抑制方法
2022-11-04张天鹏杨金钢姜海旭孙发鱼
张天鹏,谢 嘉, 杨金钢,姜海旭,孙发鱼
(1.机电动态控制重点实验室,陕西 西安 710065;2.西安机电信息技术研究所,陕西 西安 710065)
0 引言
调频引信是常见的无线电引信之一。随着无线电技术的发展,调频引信面临密集复杂的电磁环境适应性问题。线性调频(LFM)信号广泛用于雷达、通信、声呐及电子干扰装备中,在战场环境中较为常见[1]。当LFM干扰信号覆盖引信信号频谱,干扰信号经接收与引信信号下变频后可能进入引信中频处理通带,此时引信目标信号是谐波点频,干扰信号仍为LFM信号,经典的时频分析方法如短时傅里叶变换等方法难以实现目标信号与干扰的分离[2]。分数阶傅里叶变换对LFM信号有良好的聚集性[2-3],更适合用于LFM干扰抑制[4]。
FRFT实现LFM干扰抑制的原理是在最佳变换阶数下,LFM干扰在分数变换域内呈聚集状态,而目标信号为分散状态,因此在分数变换域内滤波后进行一次反变换即可得到干扰抑制后的时域信号[5-6]。文献[7]利用FRFT实现了伪码体制引信对单分量LFM干扰的抑制;但在实际场景中,干扰信号多为多分量LFM干扰。文献[8]提出了一种分数域多分量LFM干扰抑制方法,但没有考虑到干扰分量会在分数域产生的尖峰偏移现象,使干扰抑制性能下降。在上述研究背景下,本文提出一种基于信息熵的调频引信分数域干扰抑制方法,利用分数域四阶原点矩信息熵对LFM干扰信号聚集性更强,对噪声不敏感的特点,通过信息熵分级对比实现最优分数变换阶数估计,提高对干扰信号频率、调频率的分辨力,具有在低信噪比条件下更好的干扰抑制性能。
1 多分量LFM干扰信号分数域频谱分析
1.1 LFM干扰信号分数域频谱分析
LFM干扰信号模型为
x(t)=Aexp[jπ(f0t+μt2)],
(1)
式(1)中,f0为干扰信号载波频率,μ为调频率。对于有限长LFM信号,设信号的观测时间为[-Td/2,Td/2],当a≠arccot(-u)时,信号分数傅里叶变换后的幅度谱表达式分别为
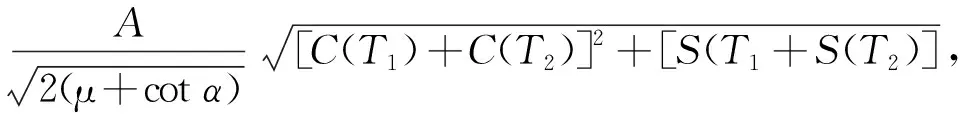
(2)
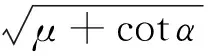
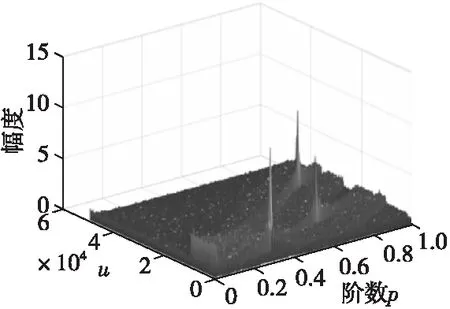
图1 多分量LFM信号分数域谱三维图Fig.1 Three dimensional fractional domain spectrum of multicomponent LFM signal
利用FRFT这一特性可实现多分量LFM干扰信号抑制,经典方法是对LFM信号连续作分数傅里叶变换,在如图1所示的(p,u)平面内极大值检测即可估计最优变换阶数,依次在最优变换域内窄带滤波完成干扰抑制。
1.2 多分量LFM干扰信号分数域尖峰偏移
多分量LFM干扰信号在分数变换域内,由于频谱相互叠加,会产生LFM干扰信号尖峰偏离其最佳变换阶数。当干扰分量的频率相近时,峰值在u轴上偏移;当调频斜率相近时,在p轴上偏移。
经典多分量LFM干扰抑制方法直接对分数变换域频谱分析,在干扰分量频率和调频斜率相近时,尖峰偏移现象会导致干扰抑制性能下降。在信噪比减小的情况下,干扰抑制性能会进一步恶化。
2 基于信息熵的调频引信分数域干扰抑制方法
2.1 分数域信息熵
经典多分量LFM干扰抑制方法在分数域频谱中估计最优变换阶数,易受尖峰偏移现象影响。为此本文提出将分数域频谱幅度转换为四阶原点矩信息熵,利用熵值估计最优变换阶数。
信号Xα(u)的四阶原点矩为
(3)
式(3)中,Td为观测时间、fs为采样率、α0为变换角度且p=2α/π。则信号Xa(u)的信息熵为[9]
(4)
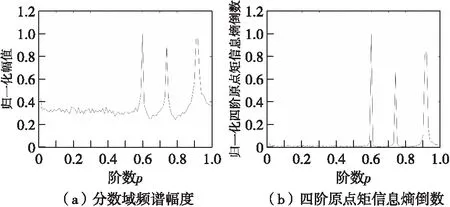
图2 两种方法归一化幅度对比Fig.2 Comparison of normalized amplitude of two methods
从图中可以看出,当α趋近于α0时四阶原点矩信息熵倒数的变化速率更快,聚集性更好,对噪声的敏感度更小。
2.2 基于信息熵的调频引信分数域干扰抑制算法
2.2.1最优变换阶数估计
经典多分量LFM干扰抑制方法需要对p∈[0,1]的分数变换域遍历搜索估计最优变换阶数,运算量较大,因此本文采用信息熵分级对比的方法估计最优变换阶数。
1)确定起始阶数位置p0与搜索步长Δp。
2)分别计算p0、p1=p0-Δp、p2=p0+Δp三个阶数的四阶原点矩信息熵倒数。
3)对比三个阶数下的四阶原点矩信息熵倒数。若1/S[γ(α1)]最大,则令p0=p1;若1/S[γ(σ2)]最大则p0=p2。重复该过程直至1/S[γ(α0)]最大。
4)令Δp=Δp/10,重复过程2),直至搜索精度满足要求即可得到最优变换阶数的估计值p0。
2.2.2基于信息熵的调频引信分数域干扰抑制算法流程
根据最优变换阶数估计方法,基于信息熵的调频引信分数域干扰抑制算法流程如图3所示。
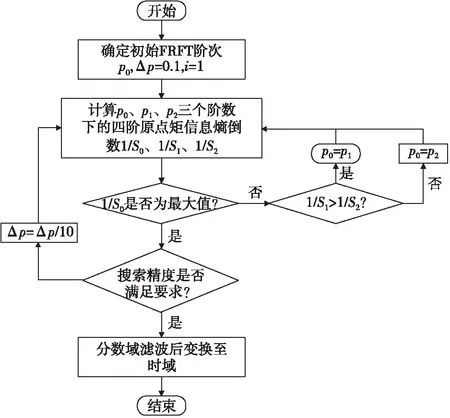
图3 基于信息熵的调频引信分数域干扰抑制算法流程Fig.3 Fractional domain interference suppression algorithm flow of FM fuze based on information entropy
3 仿真分析
3.1 运算量分析
在实际应用场景中,引信对实时性要求较高。最优变换阶数的搜索需要对信号作不同阶数下的FRFT,因此基于信息熵的调频引信分数域干扰抑制算法的运算量主要由搜索精度决定。本文采用的搜索精度Δp=0.01,最多需要计算20次分数域四阶原点矩信息熵即可得到最优变换阶数。单次分数域四阶原点矩信息熵计算需要(16N+6)lb2(2N+1)+28N次乘法运算,目前信号处理器主频大多在400 MHz以内,完成一次128点分数域四阶原点矩信息熵计算需要60 μs,因此完成一次干扰抑制算法需要的时间不大于1.2 ms,可以满足引信实时性要求。
3.2 多分量LFM干扰信号参数分辨率
1.2节分析了多分量LFM干扰分量频率、调频率相近时会产生尖峰偏移现象,本节验证基于信息熵的调频引信分数域干扰抑制方法对多分量LFM干扰频率、调频率的最小分辨力。
3.2.1频率分辨力
设置采样率为fs=100 MHz,观测时间Ts=30 μs,各LFM干扰分量调频斜率均为0.2 MHz/μs,干扰分量频率差为Δfj。对信号信噪比在-10~10 dB的区间,分别采用经典多分量LFM干扰抑制方法和基于信息熵的调频引信分数域干扰抑制方法,仿真得到产生尖峰偏移的临界值Δfjmin。图4、图5分别为干扰信号的时频分析与(p,1/S)平面。
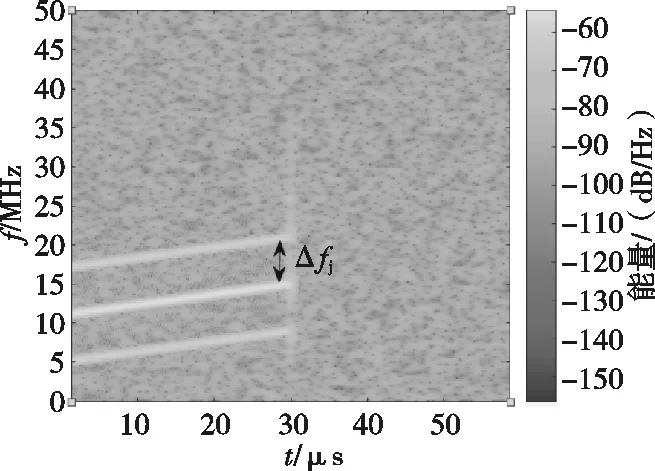
图4 多分量LFM干扰时频分析Fig.4 Time frequencyanalysis of multicomponent LFM interference
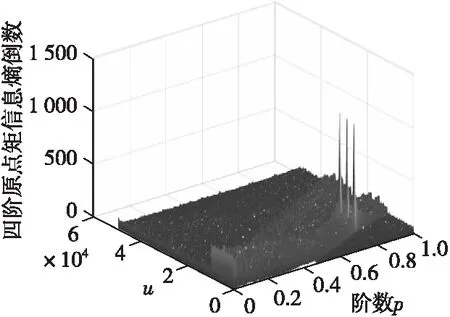
图5 干扰信号(p,1/S)平面Fig.5 Interference signal (p, 1 / s) plane
图6为两种方法Δfjmin随信噪比变化曲线。仿真结果表明,当信噪比大于4 dB时,两种方法的Δfjmin相当。在信噪比小于0 dB时基于信息熵的调频引信分数域干扰抑制方法产生尖峰偏移的临界值Δfjmin更小,对干扰信号分量的频率分辨力更好。
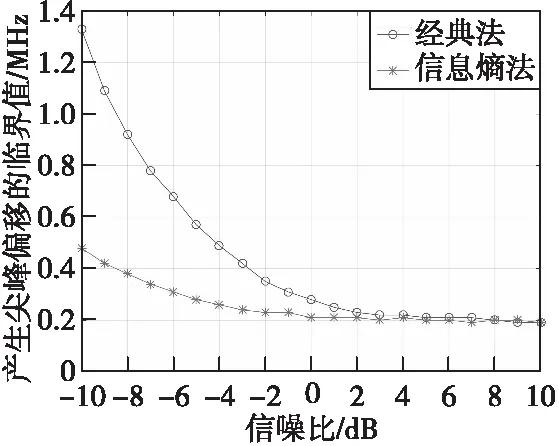
图6 两种方法Δfjmin随信噪比变化曲线Fig.6 Variation curve of signal-to-noise ratio with two methods
3.2.2调频率分辨力
设置各LFM干扰分量频率均为10 MHz,干扰分量频率差为Δμi。对信号信噪比在-10~10 dB的区间,分别采用经典多分量LFM干扰抑制方法和基于信息熵的调频引信分数域干扰抑制方法,仿真得到产生尖峰偏移的临界值Δμjmin。图7、图8分别为干扰信号的时频分析与(p,1/S)平面。
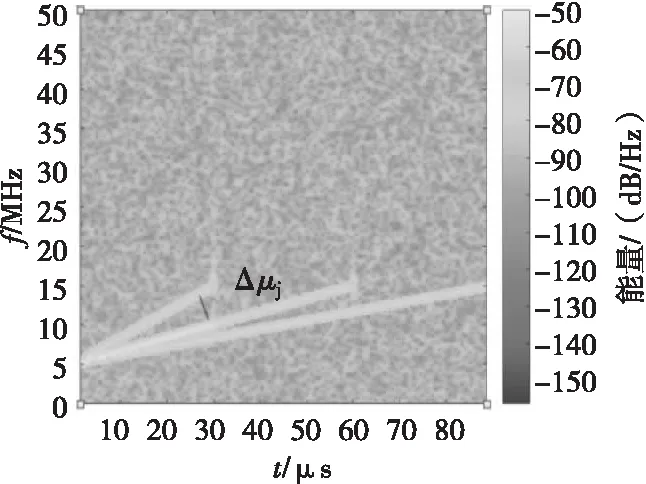
图7 多分量LFM干扰时频分析Fig.7 Time frequency analysis of multicomponent LFM interference
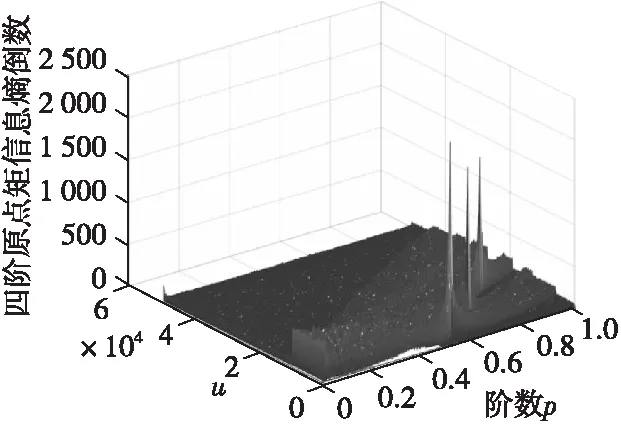
图8 干扰信号(p,1/S)平面Fig.8 Interference signal (p, 1/S) plane
图9为两种方法Δμjmin随信噪比变化曲线。仿真结果表明,当信噪比在-10~10 dB内变化时,基于信息熵的调频引信分数域干扰抑制方法产生尖峰偏移的临界值Δμjmin更小,对干扰信号分量的频率分辨力更好。当信噪比小于-2 dB时,性能提升更加明显。
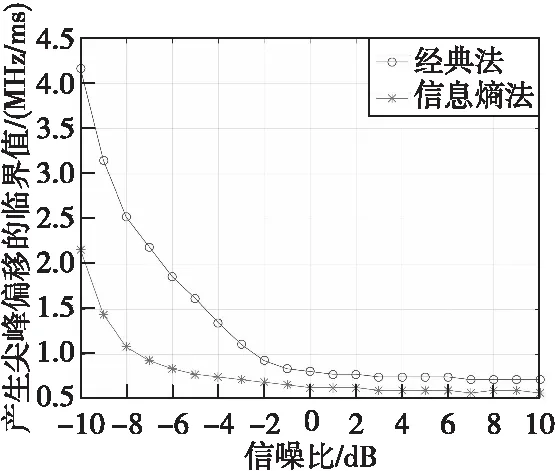
图9 两种方法Δμjmin随信噪比变化曲线Fig.9 Variation curve of two methods with signal-to-noise ratio
3.3 多分量LFM干扰抑制性能
设置各LFM干扰分量频率分别为f1=8 MHz、f2=10 MHz、f3=12 MHz,调频斜率分别为μ1=0.15 MHz/μs、μs=0.2 MHz/μs、μ3=0.25 MHz/μs,干扰分量能量相等且信干比为-10 dB。图10为两种方法在信噪比-10~10 dB内变化时,两种方法干扰抑制后的信干比随信噪比变化曲线。
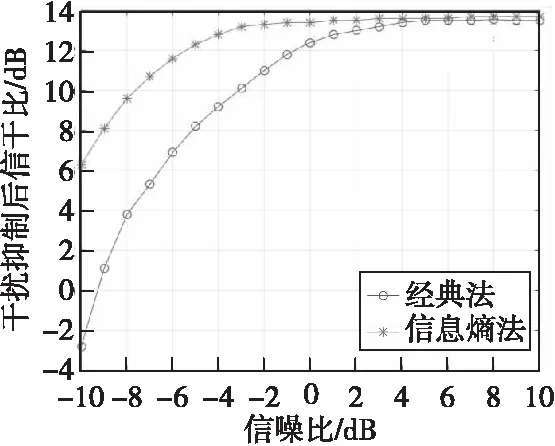
图10 两种方法干扰抑制后的信干比随信噪比变化曲线Fig.10 Variation curve of signal-to-interference ratio with signal-to-noise ratio after interference suppression by two methods
仿真结果表明:当信噪比大于4 dB时,两种方法的干扰抑制后相当;当信噪比等于-10 dB时,本文提出的方法较经典法干扰抑制后的信干比提升8.3 dB;当信噪比等于-2 dB时,干扰抑制后的信干比提升2.5 dB。因此,基于信息熵的调频引信分数域干扰抑制方法在低信噪比条件下有更好的干扰抑制性能。
4 结论
本文提出一种基于信息熵的调频引信分数域干扰抑制方法,该方法利用四阶原点矩信息熵对LFM干扰信号聚集性更强、对噪声不敏感的特点,通过四阶原点矩信息熵分级对比实现了最优分数变换阶数估计。仿真实验表明对于多分量LFM干扰信号,基于信息熵的调频引信分数域干扰抑制方法在信噪比小于0 dB时,有更好的频率分辨力,调频率分辨力。在信噪比小于-2 dB时,基于信息熵的调频引信分数域干扰抑制方法有更好的干扰抑制性能。
