露天台阶爆破开挖合理超深研究

2022-11-04马东华李智谋曲宏略

现代矿业 2022年10期

马东华左淳李智谋曲宏略

（1.湖南核工业建设有限公司；2.西南石油大学地球科学与技术学院）

超深设计值的不同会引起爆破质量的差距，超深过大很容易产生超挖现象，增加穿爆成本；超深设计过小，炮轰波无法达到台阶坡底线，易形成根底，不但增加了经济成本，还对下一步的工作造成影响。因此，研究超深问题对爆破作业设计具有重要意义［1］。当前国内外研究者对于超深的研究主要是基于工程实践的定性分析，缺乏理论的支撑，还不能够精确计算超深值，加之爆破质量的好坏受到诸多因素的影响，因而实际工程中往往使用经验参数。

本研究通过数值模拟与现场试验相结合的方法，借助LS-DYNA有限元程序［2-3］，针对孔径、超深、孔网参数，分别建立不同工况的台阶模型进行数值模拟，选取坡底线附近单元体的有效应力曲线进行对比分析，探究不同超深值对台阶爆破效果的影响［4］。

1 工程实况

该工程地势总体为北高南低，地形总体较平缓，坡度为1%～3%，局部略有起伏，地面标高为1 259.5～1 264.0 m，最大高差为4.5 m，平均标高为1 261.75 m。该场地属微倾斜戈壁平原地貌，根据工程地质钻探、标贯实验、动力触探实验并结合已有的勘探资料可知，地层主要为第四系上更新统冲洪积层砾砂夹角砾和海西中期侵入岩黑云母花岗闪长岩。

该工程先开挖土方，后爆破负挖石方，从上至下进行施工，土方开挖深度约2.0 m，采取“分区爆破，分区开挖”的方式施工，整体由南至北负挖。对现场爆破情况进行统计，所得到的爆破效果不太理想，存在部分大块和根底。

2 台阶爆破数值模拟

2.1 台阶模型

为了便于观察计算，将工程简化为平面对称问题，取1/2模型。模型总高为10 m，装药长度为4.0 m，填塞长度为3.6 m。模型由岩石、炸药、空气和填塞四部分组成，其中岩石材料采用Lagrange单元算法，炸药、空气和填塞单元使用ALE单元算法，并将这3种材料流入1个单元，再与岩石进行流固耦合。

建好模型后进行网格划分，并施加边界条件，其中台阶正面为对称面，为模拟出无限爆破区域，模型左面、右下脚面、底面和后面施加透射条件［5］，台阶顶面、坡面和坡脚设置为自由边界，不施加约束。采用g-cm-μs单位制进行建模。露天台阶三维模型见图1。

此次模拟以超深、孔径、孔网参数作为实验变量来建立三维模型，依据工程条件，孔径值选取90和110 mm；孔网参数选取3组，分别为3.0 m×2.5 m、2.8 m×2.2 m、2.5 m×2.0 m。按照经验公式，超深一般取孔径值的10～15倍，鉴于爆破现场实际情况，现场爆破后基本无根底，甚至部分爆破区域出现超挖现象，故实际超深取值相对于设计值应偏小，故选取超深值为-20，0，20 cm进行建模。按照全面搭配法的方案安排数值模拟试验，共计18种模型。

2.2 材料模型

在本次数值模拟计算过程中，采用ANSYS-LSDYNA中的164号三维实体单元构建台阶模型，对其进行网格划分，设置输出时间以及时间步长，导出K文件，借助LS-DYNA软件编辑修改K文件，赋予材料参数并定义状态方程，添加多物质材料组、设定单元算法控制、添加流固耦合关系［6］，设置起爆点后，运行求解器求解，导入结果数据文件，观察爆破应力变化情况并导出相应时程曲线和损伤图。

该拟建场地经现场勘探可知下伏基岩多为花岗岩，为方便模拟计算，选取花岗岩作为岩石材料模型，可将其视为双线性材料模型，选用岩石常用的*MAT_PLASTIC_KINEMATIC材料模型，该模型较好地描述了材料在动态冲击下的力学性能，且能够很好地模拟塑性随动强化材料［7］。

此模型以Mises准则［8］作为塑性屈服判断准则，该模型的特点是当某单元的有效应力达到屈服强度时，材料产生变形破坏，因此，将有效应力作为判断台阶爆破质量优劣的关键参数。

岩石力学参数通过室内三轴试验结果和已有的地勘资料确定，岩石力学参数见表1。

采用2号岩石乳化炸药起爆，通过材料库提供的炸药本构模型*MAT_HIGH_EXPLOSIVE_BURN描述，该模型可较为准确地描述炸药的物理力学性质，一般与炸药状态方程*EOS_JWL匹配使用，其能提供炮轰产物膨胀驱动做功的过程描述［9］。该炸药材料相关参数取值见表2。

堵塞材料参数选取塑性随动硬化模型，堵塞材料力学参数见表3。

本研究采用空物质本构模型模拟空气，同时与状态方程*EOS_LINEAR_POLYNOMIAL配合使用。

2.3 模拟步骤

本次模拟利用控制变量手段，以超深为主要实验因子，其他因素相同的情况下，以炮孔中心线作为剖面，观察台阶爆破模拟应力云图演化过程，见图2。

由台阶爆破应力演化过程可以清楚观察，台阶由孔底逐渐起爆，药包爆炸破坏作用从起爆点开始以应力波的形式向外扩散。t=140μs时，第一排孔开始起爆，t=1 000μs时，所有的孔均已起爆，当t=2 400μs时，能量扩散达到最大，大部分岩石破碎。

以动力分析有限元软件LS-DYNA作为模拟计算的工具，详细模拟了炸药爆炸过程中台阶的受力情况，选取代表性单元体，输出其有效应力时程曲线，以有效应力为判据探讨不同孔网参数和孔径情况下，超深对根底产生的影响。本研究选取台阶坡底线附近的3个单元（图3）作为监测点［10］，观察研究有效应力云图随时间的变化规律。

3 模拟结果及优化分析

3.1 孔网参数3.0 m×2.5 m模拟分析

选定孔网参数为3.0 m×2.5 m时，变换不同超深组合共有6个模型，将其逐一进行模拟，沿着台阶坡底线选取3个岩石单元，根据孔径不同将模型分为两部分进行对比分析。

3.1.1 孔径90 mm结果

单元体应力云图及台阶损伤图对应的超深均依次为0，20，-20 cm。表4为台阶模型坡底处3个单元有效应力计算结果，图4为台阶爆破的损伤图。

通过观察分析以上结果，可得到有无超深台阶爆破坡脚处的有效应力差别很大，即对爆破质量的影响很大。超深20 cm时的有效应力比超深为-20 cm的有效应力大，且超深越小，选取的部分单元体的有效应力均值越小，3组模型的应力均值均未超过抗拉强度，岩石未破碎，留下一定的根底。

3.1.2 孔径110 mm结果

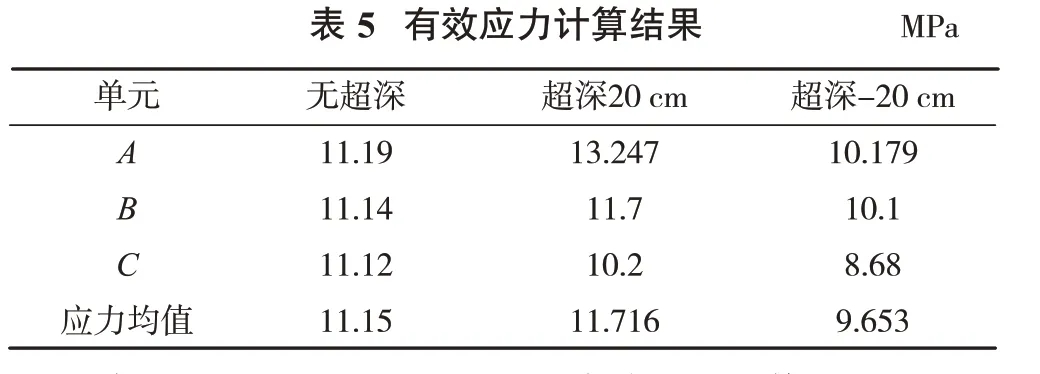
孔网参数为3.0 m×2.5 m，孔径为110 mm，建立3组台阶模型，通过后处理软件计算得到监测点的有效应力结果，将这3组模型中每组的每个单元最大有效应力值进行整理，见表5。

当超深为20 cm时，有效应力均值为11.716 MPa，是3组模型中观测单元体有效应力最大的，即爆破模拟效果最佳。通过观察台阶损伤云图，更加直观地展示了爆破后的破碎效果，见图5。

在这2组模型中，超深20 cm、孔径110 mm时有效应力峰值最大，单元最大有效应力均值最大为11.716 MPa，其对应的台阶损伤云图的损伤分布情况最为破碎，可能存在一定程度的超挖现象。

3.2 孔网参数2.8 m×2.2 m模拟分析

孔网参数为2.8 m×2.2 m时，变换不同超深孔径组合共有6个模型。根据孔径不同将其分为2组模型分析。

3.2.1 孔径90 mm结果

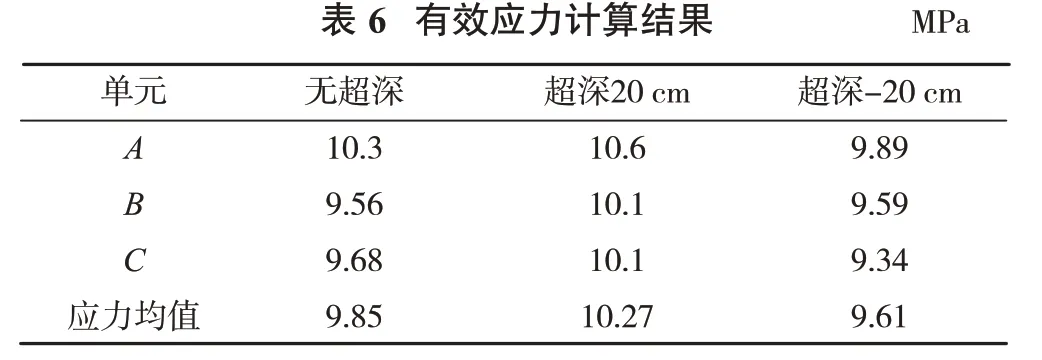
将超深作为唯一变量进行数学建模，数值模拟输出监测点单元A、B、C有效应力随时间变化的曲线，对应的监测点有效应力峰值汇总情况见表6。

可以看出，该孔网参数下的监测点有效应力总体要比同孔径、孔网参数为3 m×2.5 m的有效应力小一些。从有效应力最大值汇总结果可以看出，爆后坡底线的平均应力均大于岩石抗拉强度。超深-20 cm、孔径90 mm时有效应力最小，有效应力均值为9.61 MPa。超深为20 cm、孔径为90 mm时单元有效应力最大，有效应力均值为10.27 MPa。

为进一步研究超深20 cm，孔径90 mm工况下的爆破质量好坏，绘制了其爆破损伤云图，见图6。

由图6可见，台阶岩体破碎情况较完整，大块状岩石较少，存在部分超挖现象，但相对而言整体爆破质量较好。

3.2.2 孔径110 mm结果

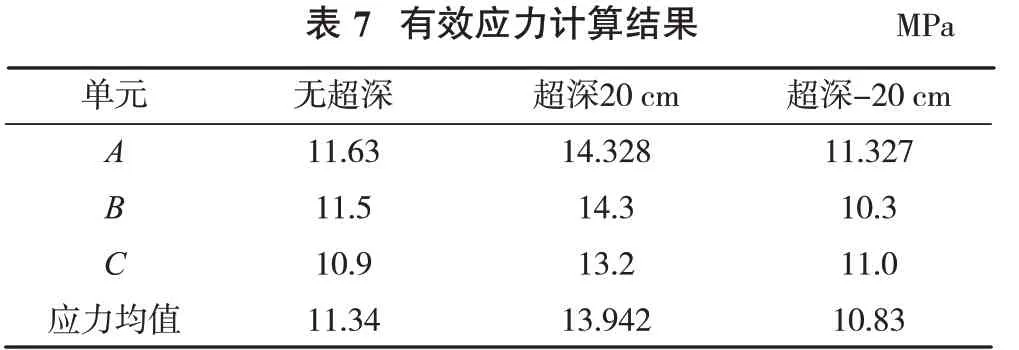
以孔径110 mm，超深0，-20，20 cm为变化参数列出3组模型，选取A、B、C单元体查看其有效应力随时间变化的曲线，依据单元体有效应力—时间曲线记录其各监测点应力峰值。具体数据见表7。

结果表明，孔径为110 mm时，监测点的单元有效应力均值均超过了岩石的屈服强度，证明此工况下的岩石均完全破碎。超深对爆破根底的影响规律与前述一致。

为更好地了解岩石破损情况，通过数值模拟分析得到台阶破损图，见图7。

观察损伤图都有一个共同点，就是损伤演化的规律基本一致，均存在着炮孔附近的岩体损伤最严重的情况。应力波以起爆点为中心向四周传播，岩体逐渐出现裂纹，随着时间历程，两炮孔之间的岩体受到应力波叠加作用，在压缩波的作用下岩体逐渐破碎，形成粉碎区；粉碎区形成后进入裂隙区，当应力波在自由面处将会发生倒向，形成拉伸波，损伤裂隙进一步扩展延伸，逐渐形成岩块脱离岩体。除此之外，还可通过损伤云图看出2组模型岩体损伤情况与有效应力判据下的岩石破碎情况相符合。坡脚处台阶模型存在着许多裂隙，岩石松动剥落，形成部分大块，台阶顶面左上角、坡面右后方均存在大块。

对比90 mm、孔径110 mm的2组模型的应力情况和损伤图，得到虽然110 mm孔径的岩体破碎情况更完整，但考虑到大孔径所需要的价格和装药量因素，加之孔径90 mm、超深20 cm时的爆破效果与其基本一致，故而选择较为经济的方案，即孔径90 mm、超深20 cm。

3.3 孔网参数2.5 m×2.0 m模拟分析

模型以孔径为划分依据分为2组，超深分别对应0，20，-20 cm。对2组模型进行数值模拟，分析计算有效应力结果。

3.3.1 孔径90 mm结果

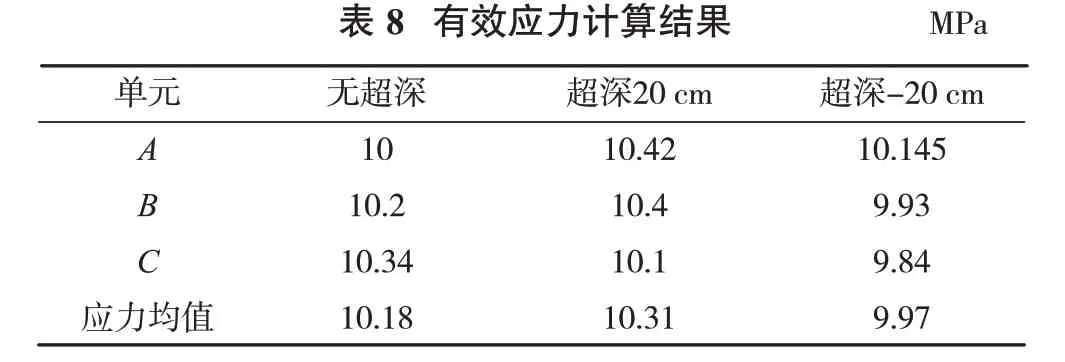
根据本组模型对应的A、B、C爆破单元体有效应力—时间曲线图，整理记录其各监测点应力峰值。具体数据见表8。

在孔网参数为2.5 m×2.0 m、孔径90 mm时，除了超深为-20 cm应力均值未超过10 MPa，其余2组的有效应力均超过10 MPa，即岩石破碎。其中无超深时，单元最大有效应力的最大值为10.34 MPa，最小值为10 MPa，均值为10.18 MPa，爆破效果最佳，具体效果见台阶损伤图8。

3.3.2 孔径110 mm结果

建立超深不同的模型，输出监测点对应的有效应力曲线分析爆破效果。该组模型对应的考察单元体A、B、C有效应力时程曲线的应力峰值统计结果见表9。

对于孔网参数为2.5 m×2.0 m时，孔径110 mm的单元最大有效应力的最大值为14.769 MPa，最小值为10.77 MPa，都超过了岩石抗拉强度10 MPa，此时岩石破碎。根据损伤图可见该工况下存在明显的超挖现象（图9）。

由台阶损伤云图对比分析可得，随着超深的增加根底现象明显改善。孔径为110 mm时的台阶破损质量相对孔径90 mm而言，超挖现象更为严重，爆破质量较差。当孔网参数为2.5 m×2 m、孔径90 mm、超深为0 cm时，单元最大有效应力的最大值为10.34 MPa，最小值为10 MPa，均值为10.18 MPa，都超过了岩石抗拉强度10 MPa，此时岩石破碎，且几乎无超挖大块率问题，爆破效果最佳。

4 应用实例

综合以上分析结果，为避免超挖，选择较保守的爆破参数进行试验，即孔网参数2.5 m×2.0 m、孔径90 mm、超深为0 cm。爆破后进行数据统计，发现与原爆破方案（孔网参数3.0 m×2.5 m，孔径90 mm，超深为20 cm）对比，采用优化后孔网参数进行爆破，大块率降低了20%，根底率降低了15%，最终爆破效果符合预期，有效提高了工作效率。