基于水文-气象阈值的区域降雨型滑坡预测研究

赵彬如，陈恩泽，戴 强，朱少楠，张 君

1. 南京师范大学地理科学学院，江苏 南京 210023； 2. 虚拟地理环境教育部重点实验室(南京师范大学)，江苏 南京 210023； 3. 江苏省地理信息资源开发与利用协同创新中心，江苏 南京 210023； 4. 南京邮电大学地理与生物信息学院，江苏 南京 210023

滑坡是我国主要的地质灾害之一，滑坡灾害每年都会造成巨大的经济损失和人员伤亡，严重制约着国民经济的建设及社会的发展[1-4]。据《中国统计年鉴—2020》显示，2010—2019年十年间我国共发生滑坡灾害88 084起，占地质灾害总数的71.3%。滑坡的发生除了受自身地质条件的影响外，还受地震、降雨、洪水及人类活动等多种诱发因素的影响与控制，其中降雨诱发的滑坡(即降雨型滑坡)占滑坡总数的90%左右[5]。2019年贵州水城“7·23”特大山体滑坡灾害的主要诱因就是强降雨，造成近1600人受灾，43人死亡，9人失踪，直接经济损失1.9亿元[6]。随着极端气候事件特别是极端降雨事件的增加，降雨诱发滑坡的频率和危害程度也不断加剧，对人民生命财产安全造成严重威胁。滑坡预测作为重要的非工程性措施，可为滑坡灾害风险管理和决策制定提供科学依据，对于防灾减灾具有重要意义。

降雨型滑坡预测主要基于降雨与滑坡之间的关系开展，包括统计分析法和物理模型法[7-8]。统计分析法通过对历史滑坡事件的降雨信息进行统计分析，得到可能诱发滑坡的最小降雨条件，即经验性降雨阈值，并以此作为滑坡预测的依据[9-11]。物理模型法基于降雨型滑坡发生的物理机制，通过考虑降雨发生前后的地下水位变化、土壤湿度变化及相应的应力变化，用动力学方法实现滑坡预测[12-14]。虽然物理模型法可以充分考虑降雨诱发滑坡的物理机制，但因其需要输入详细的水文地质参数，计算量大，一般只适用于单个边坡的滑坡预测。基于统计分析法的经验性降雨阈值是目前区域降雨型滑坡预测中最常用的工具[15]，降雨阈值的主要表现形式为基于降雨事件变量的降雨阈值曲线，例如广泛使用的降雨历时-降雨强度阈值曲线、降雨历时-累积降雨量阈值曲线[16-18]。随着降雨阈值在实践应用中的推广，其存在的不足也逐渐被知晓，例如，降雨阈值曲线在滑坡预测中常常表现出较高的误报率[19-20]。如何改进降雨阈值以提高区域滑坡预测的准确性和可靠性，已成为学者们普遍关注的热点问题。

降雨诱发滑坡的实质是降雨入渗导致土壤含水量重新分布及有效应力改变，当边坡的应力状态达到其极限强度时就可能导致滑坡[21]。从该机理可知，除降雨入渗导致的土壤含水量变化外，降雨入渗前的土壤含水量也是影响边坡失稳的重要因素，因此无法考虑降雨入渗前的土壤湿度情况，被认为是降雨阈值曲线在滑坡预测中表现差的主要原因。由此可知，充分考虑前期土壤湿度和近期降雨在滑坡发生过程中的共同作用，构建基于前期土壤湿度和近期降雨的阈值模型(也称为水文-气象阈值模型)，是改进降雨阈值滑坡预测效果的可行思路[22]。文献[23]利用分布式水文模型模拟土壤湿度数据，并通过分析与滑坡有关的土壤湿度及降雨信息，为美国中部某流域确定了预测滑坡的阈值曲线，证明了基于土壤湿度及降雨信息建立的阈值模型在滑坡预测中的有效性。文献[24]将实时水文监测获取的土壤湿度与降雨情况相结合来确定滑坡阈值表达式，该阈值模型在滑坡预测中表现较好。文献[25]用流域蓄水容量来表示前期土壤湿度情况，并基于流域蓄水容量和降雨事件在意大利北部某流域建立了预测滑坡的阈值模型，通过与传统的降雨强度-历时关系阈值进行比较，发现水文-气象阈值有较优的预测能力。

虽然水文-气象阈值已被证明可以有效改善降雨阈值的滑坡预测性能，但其在实践中的应用仍然较少，主要原因是相比于降雨数据，土壤湿度数据较难获取[26]。当土壤湿度数据不可用时，如何科学合理地表征前期土壤湿度情况，是构建水文-气象阈值的关键。本文尝试用改进的前期有效降雨指数来表征前期土壤湿度情况，并通过统计分析历史滑坡数据和前期有效降雨指数及近期降雨之间的关系，构建可能诱发降雨型滑坡的最小水文-气象阈值模型，实现区域降雨型滑坡预测，以期改善降雨型滑坡预测的准确性，对降低滑坡灾害造成的损失具有十分重要的现实意义。

1 研究方法

1.1 土壤湿度指标的计算

前期有效降雨指数(antecedent precipitation index,API)是一个基于前期有效降雨量的变量，由于具有对数据要求少、计算简单等特点，常被用作表征土壤湿度情况的指标，其最常见的形式[27]是

APIt=k·APIt-1+Pt

(1)

式中，APIt为第t天的前期有效降雨指数，单位为mm；Pt为第t天的降雨量，单位为mm；k为衰减系数，用于反映由蒸发、径流等造成的降雨损失。

文献[28]指出，从水文学的角度，在计算前期降雨对土壤湿度的贡献时，可以从两方面改进式(1)以更好地反映实际物理过程。

第一，假定式(1)中的衰减系数为常数，与实际物理过程不符，衰减系数在这里用于反映由蒸发、径流等造成的降雨损失，而蒸发等过程因受多种因素的影响在实际中是不断变化的，例如气温较高时蒸发较多，而气温较低时蒸发较少，因此假定衰减系数为常数忽略了降雨损失随多种因素的变化，进而影响前期有效降雨指数在表征土壤湿度方面的表现。针对该问题，文献[28]提出了随气温变化的衰减系数，并假定衰减系数随气温呈线性变化

k=0.84+δ(20-Tave)

(2)

式中，Tave为日平均气温，单位为℃；δ为敏感系数，单位为℃-1。当δ=0时，衰减系数k为常数0.84。0.84是文献[29]推荐的值，后来被广泛应用于计算前期有效降雨指数，在衰减系数取0.84的案例中，平均气温为20℃左右，这也是式(2)的由来。

第二，用式(1)计算前期有效降雨指数时，没有考虑土壤最大含水量的影响。在水文过程中，当暴雨径流等的汇集使土壤达到或接近饱和时，落在这些面积上的降雨便会产生地表径流，即蓄满产流，此时土壤含水量不再改变，而式(1)因没有考虑土壤最大含水量的影响在表征土壤湿度情况时会产生高估的现象。因此，文献[28]通过引入参数APImax来考虑土壤最大含水量的影响

(3)

本文采用上述介绍的改进的前期有效降雨指数来表征前期土壤湿度情况，其中参数δ和APImax采用遥感土壤湿度θ来率定，并以皮尔逊相关系数作为评价指标，即对参数δ和APImax随机取值，生成若干个参数组合，并基于每个参数组合计算API，当API和遥感土壤湿度θ的皮尔逊相关系数最大时得到的参数即为最优参数，其中皮尔逊相关系数的计算公式为

(4)

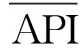
1.2 水文-气象阈值的构建

本文在构建用于滑坡预测的水文-气象阈值模型时，分别用改进的前期有效降雨指数和近期累积降雨量来表征前期土壤湿度和近期降雨情况，通过参照已有相关研究[24,30-31]，假定由前期有效降雨指数和近期累积降雨量组成的阈值表达式为线性关系

P=aS+b

(5)

式中，P为近期累积降雨量，单位为mm；S为用前期有效降雨指数表征的前期土壤湿度，单位为mm；a为斜率且a≠0；b为上述函数在y轴上的截距。

为得到有效的阈值表达式，首先需计算P和S两个变量，然后确定参数a和b的取值，如图1所示。

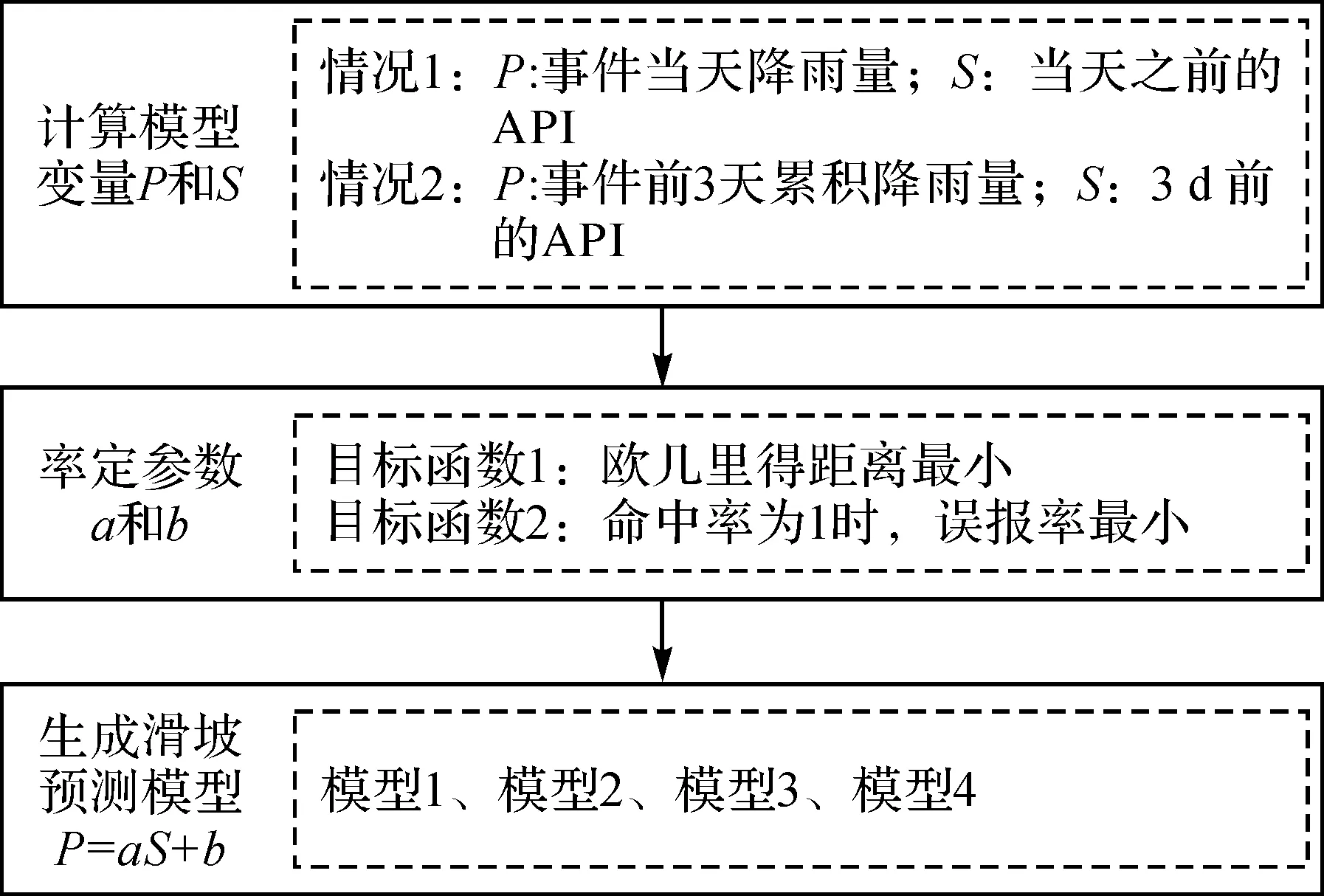
图1 滑坡预测模型的技术流程Fig.1 The flowchart of landslide prediction model

在计算P和S两个变量时，需定义近期与前期的界限，从已有研究来看，大部分情况下近期指事件当天或事件前3 d(包括事件当天)，而对应的前期分别为当天之前或前3 d之前。文献[5]在确定预测滑坡的阈值表达式时用事件当天的降雨量作为近期降雨量。文献[24，32]则用事件前3 d(包括事件当天)的降雨量作为近期降雨量。近期与前期的划分可能会对阈值模型的滑坡预测性能造成影响，因此，本文在确定水文-气象阈值表达式时，分别考虑两组情况，一组为用事件当天的降雨量作为近期降雨量，而用当天之前的前期有效降雨指数来表征前期土壤湿度情况；另一组为用事件前3 d(包括事件当天)的累积降雨量作为近期降雨量，而用3 d前的前期有效降雨指数来表征前期土壤湿度情况。

为确定式(5)中a和b的最优取值，本文假定a和b的多种取值组合，通过选取不同目标函数来评估基于不同取值的阈值表达式的滑坡预测表现，可得到最优滑坡预测表现对应的a和b的最优取值，即得到水文-气象阈值模型的阈值表达式。评估所用方法如图2所示，以每一天作为一个事件，首先计算出每一个事件的变量，即近期累积降雨量及前期有效降雨指数；然后假定一组a和b的取值来确定阈值表达式，通过比较事件的变量与阈值表达式的关系，可以判断该事件属于真正类(true positive,TP)、假负类(false negative,FN)、假正类(false positive,FP)或真负类(true negative,TN)中的哪种情况。如果事件的变量位于阈值表达式之上，且在实际中有滑坡发生，则该事件属于真正类；如果事件的变量位于阈值表达式之上，但在实际中没有滑坡发生，则该事件属于假正类；如果事件的变量位于阈值表达式以下，但在实际中有滑坡发生，则该事件属于假负类；如果事件的变量位于阈值表达式以下，且在实际中没有滑坡发生，则该事件属于真负类。在得到每个事件的分类情况后，可以计算得到命中率、误报率及欧几里得距离等评价指标，具体计算公式分别见式(6)、式(7)和式(8)。命中率越高且误报率越低时，阈值表达式的预测性能越好，此时欧几里得距离也越小。在实际中，为了避免漏报造成的影响，通常将命中率限制为最优值1，此时，误报率越低，阈值表达式的预测性能越好。因此，本文在确定参数a和b的最优取值时，选用两种目标函数：①欧几里得距离最小；②命中率为1时，误报率最小。

(1) 命中率，也被称为真正类率(true positive rate,TPR)，用于计算被正确预测的滑坡事件在所有滑坡事件中的比例，最优值为1，计算公式为

(6)

(2) 误报率，也被称为假正类率(false positive rate,FPR)，用于计算被误报的事件在没有滑坡发生的事件中的比例，最优值为0，计算公式为

(7)

(3) 欧几里得距离。当命中率为1且误报率为0时，滑坡预测模型的预测结果最优。但在实际情况中，模型的预测结果很难达到最优，此时通过计算模型的预测结果与最优值之间的欧几里得距离(d)来评估模型的表现，距离越小，模型表现越好。欧几里得距离的计算公式为

(8)

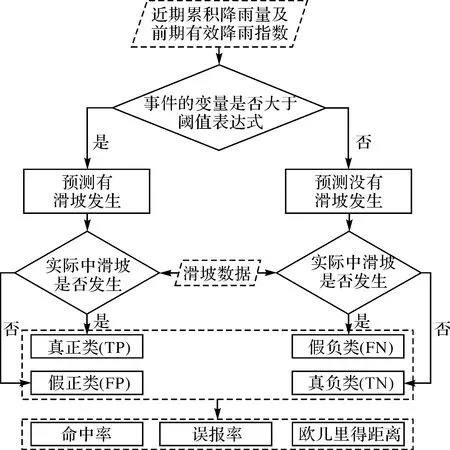
图2 滑坡预测模型的评估流程Fig.2 The flowchart of the evaluation of landslide prediction model

2 试验区域与数据

2.1 试验区域

为了验证上述方法在预测区域降雨型滑坡方面的有效性，本文选用四川省都江堰地区作为试验区域。都江堰地区位于四川省中部成都平原的西北边缘，东南距成都市48 km。地理坐标为103°25′E—103°47′E，30°44′N—31°22′N，东西最大横距54 km，南北最大纵距68 km，幅员面积1208 km2，区域内最高海拔4443 m，最低海拔570 m，相对高差为3873 m(图3)。

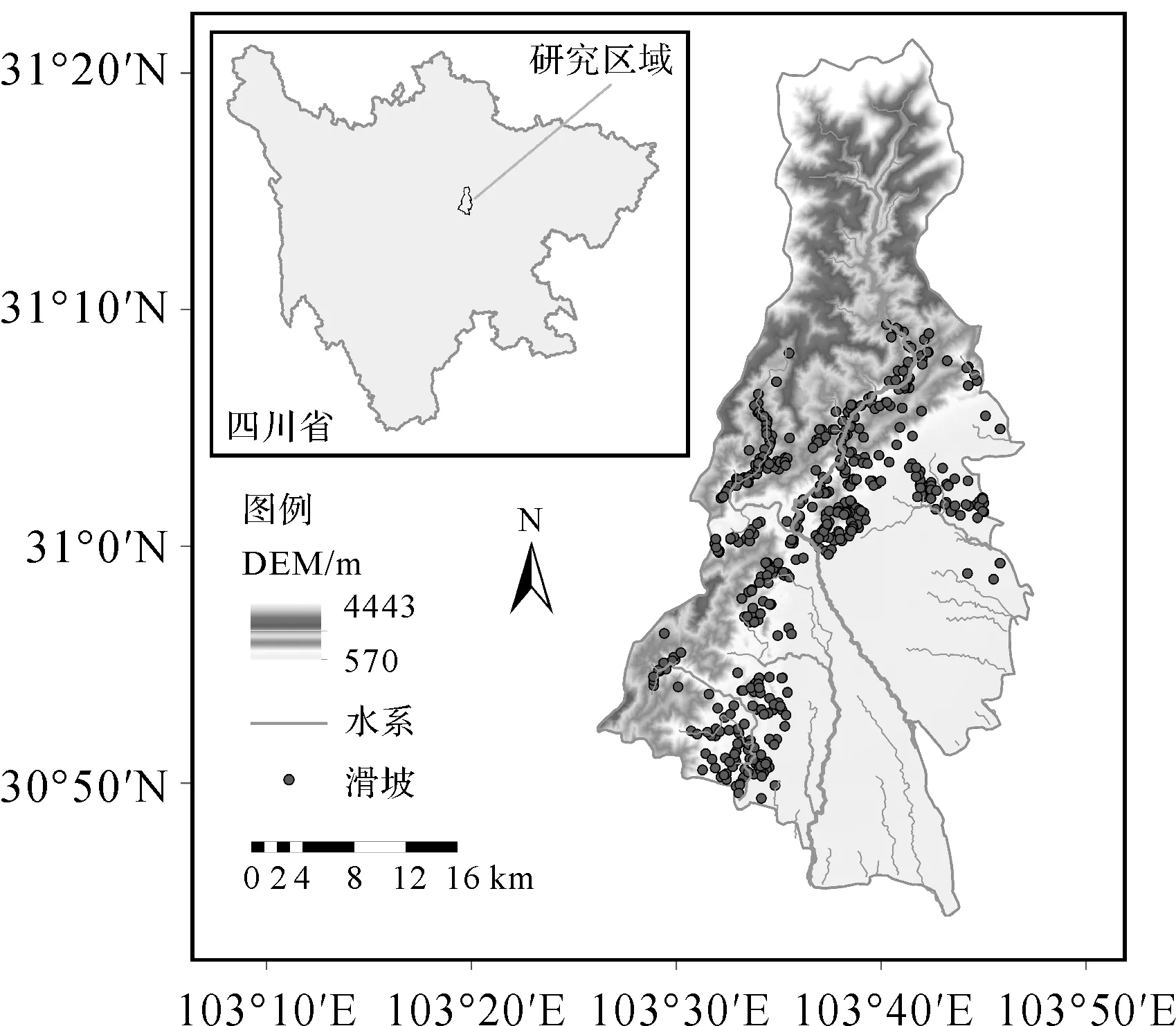
图3 试验区域内2009—2016年滑坡的位置分布Fig.3 Distribution of landslides in the study area from 2009 to 2016

都江堰地区部分区域地形陡峭、岩体破碎且地震活动频繁，地质环境较为脆弱，在人类活动及持续强降雨等因素作用下极易发生滑坡灾害，建立适用于该地区的降雨型滑坡预测模型对于防灾减灾具有重要意义。

2.2 数据概况

本文研究涉及的数据包括两大类：水文气象数据与滑坡数据。

水文气象数据包括以24 h为时间尺度的降雨、气温及土壤湿度数据。降雨及气温数据来自都江堰气象监测站，该站点的地理坐标为103°4′E，31°N，海拔698.5 m，数据从中国气象数据网(https:∥data.cma.cn/)获取。土壤湿度数据采用遥感产品ESA Climate Change Initiative (CCI) soil moisture product，记作CCI-SM，从https:∥www.esa-soilmoisture-cci.org/获取，本文采用的是综合主动及被动微波观测信息的CCI-SM COMBINED产品，该产品的空间分辨率为0.25°×0.25°，时间分辨率为24 h，本文研究所用的CCI-SM数据为位于103°37′E，31°7′N处的数据。

滑坡数据由中国科学院·水利部成都山地灾害与环境研究所(简称“成都山地所”)提供，包括2009—2016年在试验区域内发生的各种规模的滑坡，共计499个，其中多个滑坡发生在同一天，且地理位置接近(图3)，多集中在河流附近。

图4展示了试验区域内2009—2016年滑坡及降雨的月分布，由滑坡的月分布可以发现滑坡主要集中发生在7、8月，共481个，约占总滑坡数量的96%，由降雨的月分布可知7、8月是试验区域内降雨最多的月份，滑坡分布与降雨分布的吻合说明在试验区域降雨是诱发滑坡的主要因素。一般认为发生在降雨集中期的滑坡为降雨型滑坡，由于本文的研究对象为降雨型滑坡，以下研究中所用滑坡数据为2009—2016年7、8月的滑坡数据。

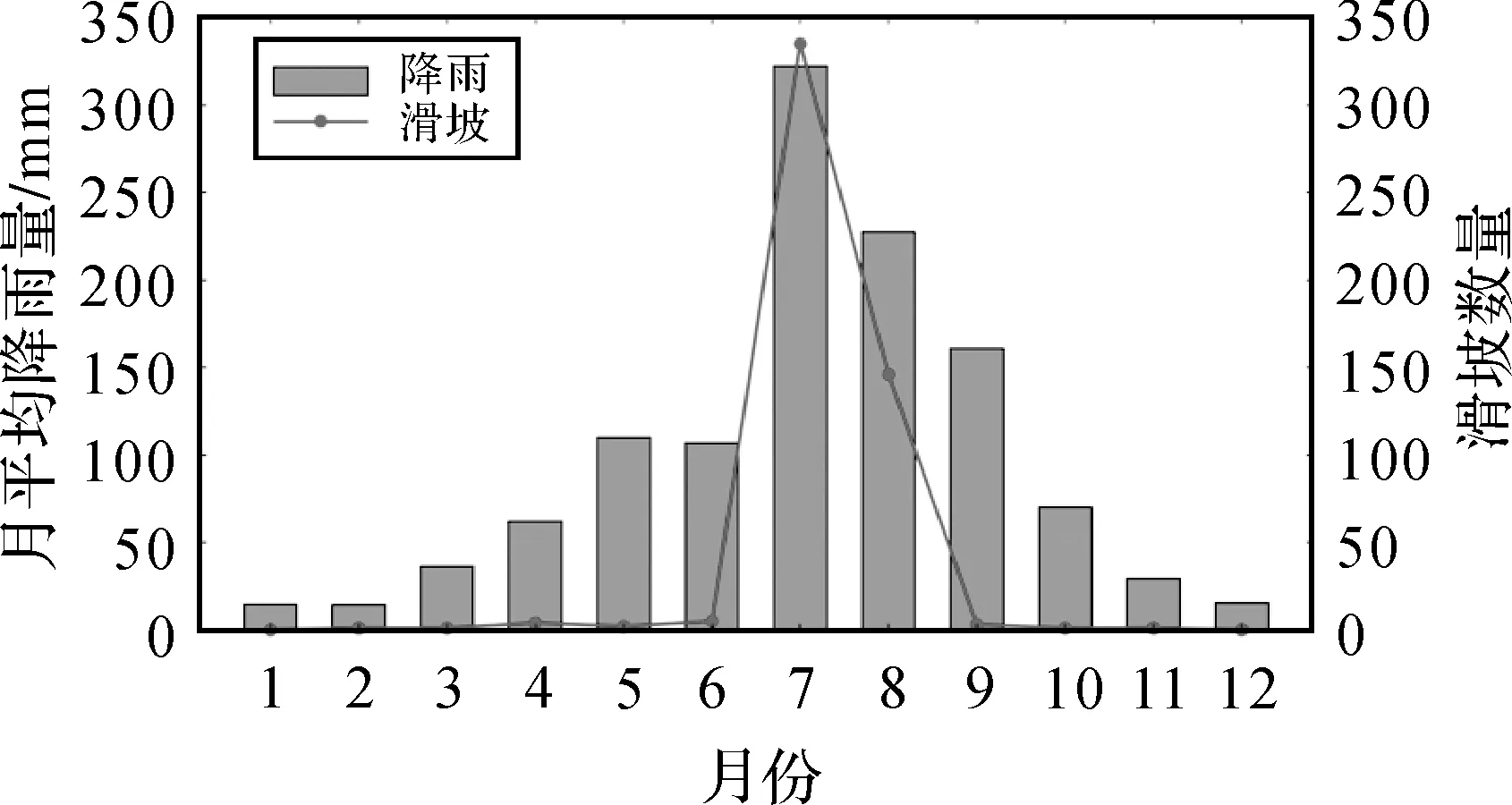
图4 试验区域内2009—2016年月平均降雨量与滑坡数量分布Fig.4 Monthly rainfall and quantity of landslide in the study area from 2009 to 2016

进一步分析7、8月的滑坡数据可知，尽管在2009—2016年7、8月共有481个滑坡发生，但发生滑坡的天数仅有24 d，即有大量滑坡是由同一场降雨诱发的，例如，2010年8月13日有125个地点发生滑坡，而在2013年7月9日有316个地点发生滑坡。本文将发生在同一天的滑坡归为一个滑坡事件，因此共有24个滑坡事件。图5展示了2009—2016年降雨、土壤湿度的时间序列及滑坡事件的分布，由图5可知，几乎所有滑坡事件的发生都伴随着集中降雨，且滑坡事件的前期土壤湿度较高。

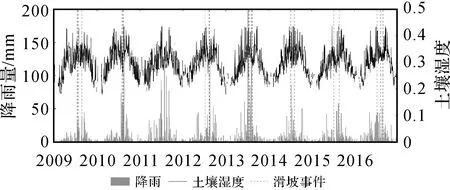
图5 2009—2016年降雨及土壤湿度的时间序列及滑坡事件的分布Fig.5 Time series of rainfall, soil moisture and distribution of landslide events from 2009 to 2016

3 结果分析

3.1 土壤湿度指标

由于前期有效降雨指数的计算公式为递推公式，首先要确定计算公式中的初始时刻和初始值，根据文献[28]的研究成果，当初始时刻选60 d前时，APIt-60的取值对APIt几乎没有影响，本文选取试验区域API的平均水平15 mm作为APIt-60的初始值。

本文在率定改进的前期有效降雨指数中的参数δ和APImax时，采用2009—2014年土壤含水量的遥感数据作为评判基准，皮尔逊相关系数作为评价指标，在确定了δ和APImax的最优值后，用2015—2016年土壤含水量的遥感数据验证参数的有效性，仍以皮尔逊相关系数作为评价指标。经率定，δ和APImax的取值分别为0.008℃-1和22 mm。图6分别展示了研究区域率定期和验证期内前期有效降雨指数与土壤含水量的散点图，可以看出，不管是在率定期还是验证期，前期有效降雨指数与土壤含水量都有较好的线性相关关系，皮尔逊相关系数分别为0.72和0.76。验证期内前期有效降雨指数与土壤含水量较好的线性相关关系表明率定的参数在用独立数据验证时仍然有效。

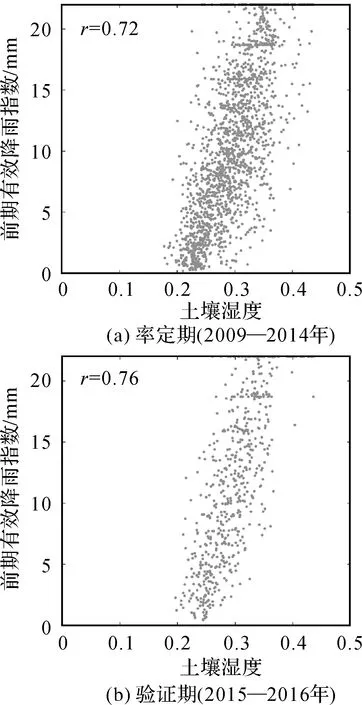
图6 试验区域前期有效降雨指数与土壤含水量的散点分布Fig.6 Scatter plot of API and soil water content in the study area

3.2 水文-气象阈值

3.2.1 近期与前期的分界为1 d

当用事件当天的降雨量作为近期降雨量，当天之前的前期有效降雨指数来表征前期土壤湿度情况时，通过评估不同阈值表达式的滑坡预测能力，得到的最优阈值表达式为

P1=4.7-0.01S1

(9)

P1=6.9-0.37S1

(10)

式中，P1为事件当天的降雨量，单位为mm；S1为事件前一天的前期有效降雨指数，单位为mm。

式(9)所示的阈值表达式是在评价指标欧几里得距离最小时得到的，称为模型1，而式(10)所示的阈值表达式是在限制命中率为1的情况下，误报率最低时得到的，称为模型2。图7展示了这两种模型对应的阈值曲线及相关事件的分布，其中滑坡事件的近期降雨量及前期有效降雨指数见表1。由表1可知，滑坡发生当天的降雨量最小为0 mm，而最大可达423.80 mm，也就是说，即使当天的降雨量很小，滑坡也有可能发生，例如，2016年8月10日的滑坡事件，当天降雨量为0 mm，但其前期有效降雨指数为22 mm，即前期有效降雨指数的最大值，这意味着前期降雨已使斜坡土体处于饱和状态，在降雨很小或没有降雨的条件下，滑坡也有可能发生。观察前期有效降雨指数的取值可以发现，尽管该指数的变化范围为8.6～22 mm，该指数取值为22 mm的事件有10个，约占总滑坡事件的42%，说明当前期土壤湿度处于饱和状态时，滑坡较容易发生。另一方面，当前期土壤湿度较低即前期有效降雨指数较小时，滑坡也有可能发生，例如，2009年8月13日的滑坡事件，即使前期有效降雨指数的取值仅为8.65 mm，但其对应的近期降雨量为38.90 mm，说明在该滑坡事件中，滑坡当天的降雨量起到了决定性作用。由以上分析可知，前期土壤湿度情况和近期降雨对滑坡的发生都具有重要意义，进一步说明在确定滑坡预测模型的阈值表达式时很有必要同时考虑这两个变量。

由图7可以看出，对于模型1的阈值曲线，当事件的前期有效降雨指数为0 mm时，如果事件当天的降雨量超高4.7 mm，则认为滑坡有可能发生；而对于模型2的阈值曲线，当事件的前期有效降雨指数为0 mm时，如果事件当天的降雨量超高6.9 mm，认为滑坡有可能发生。

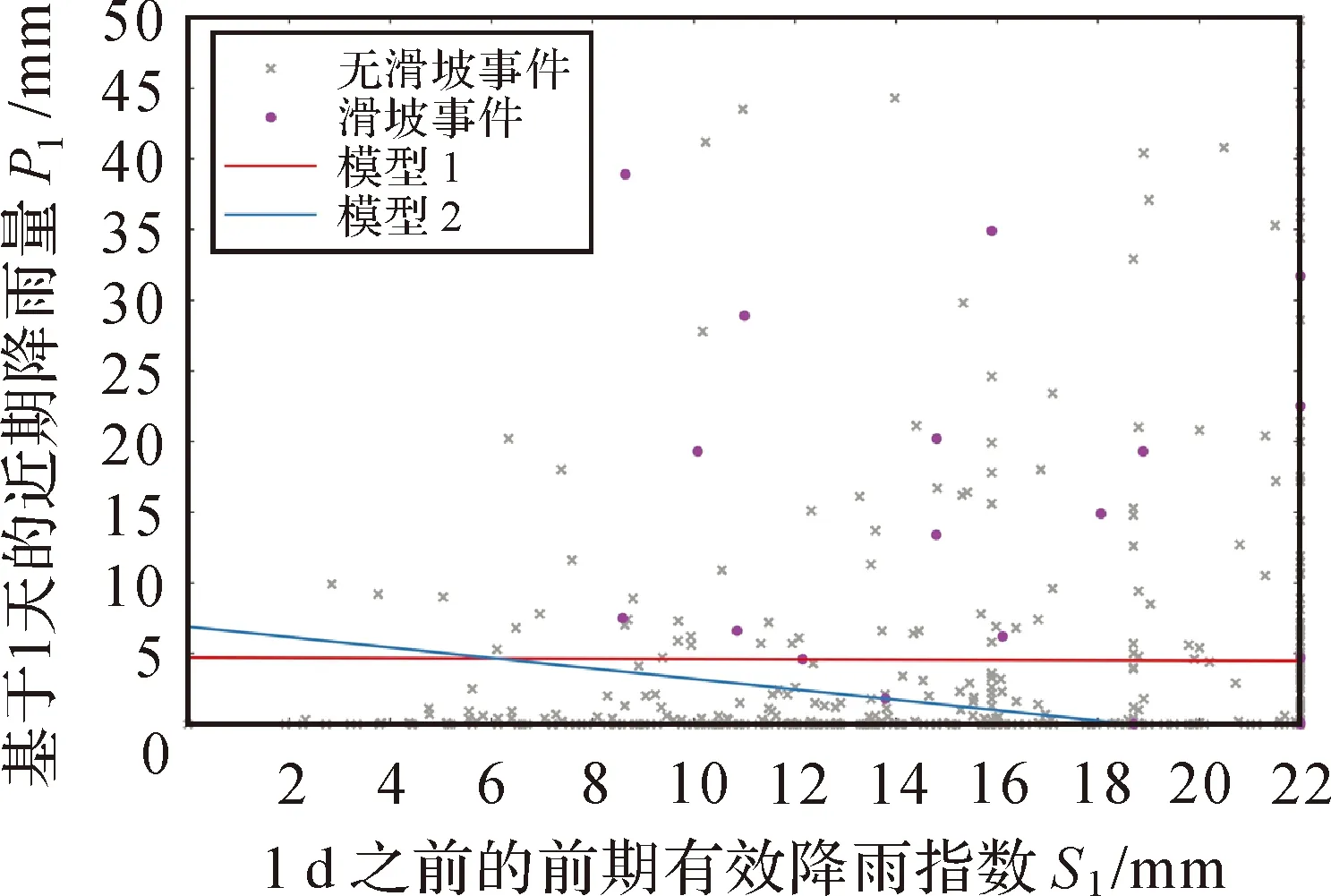
图7 基于近期降雨和前期有效降雨指数的水文-气象阈值曲线(近期与前期的分界为1 d)Fig.7 Hydro-meteorological threshold curve based on the recent cumulated rainfall and API (The boundary between recent period and antecedent period is one day)

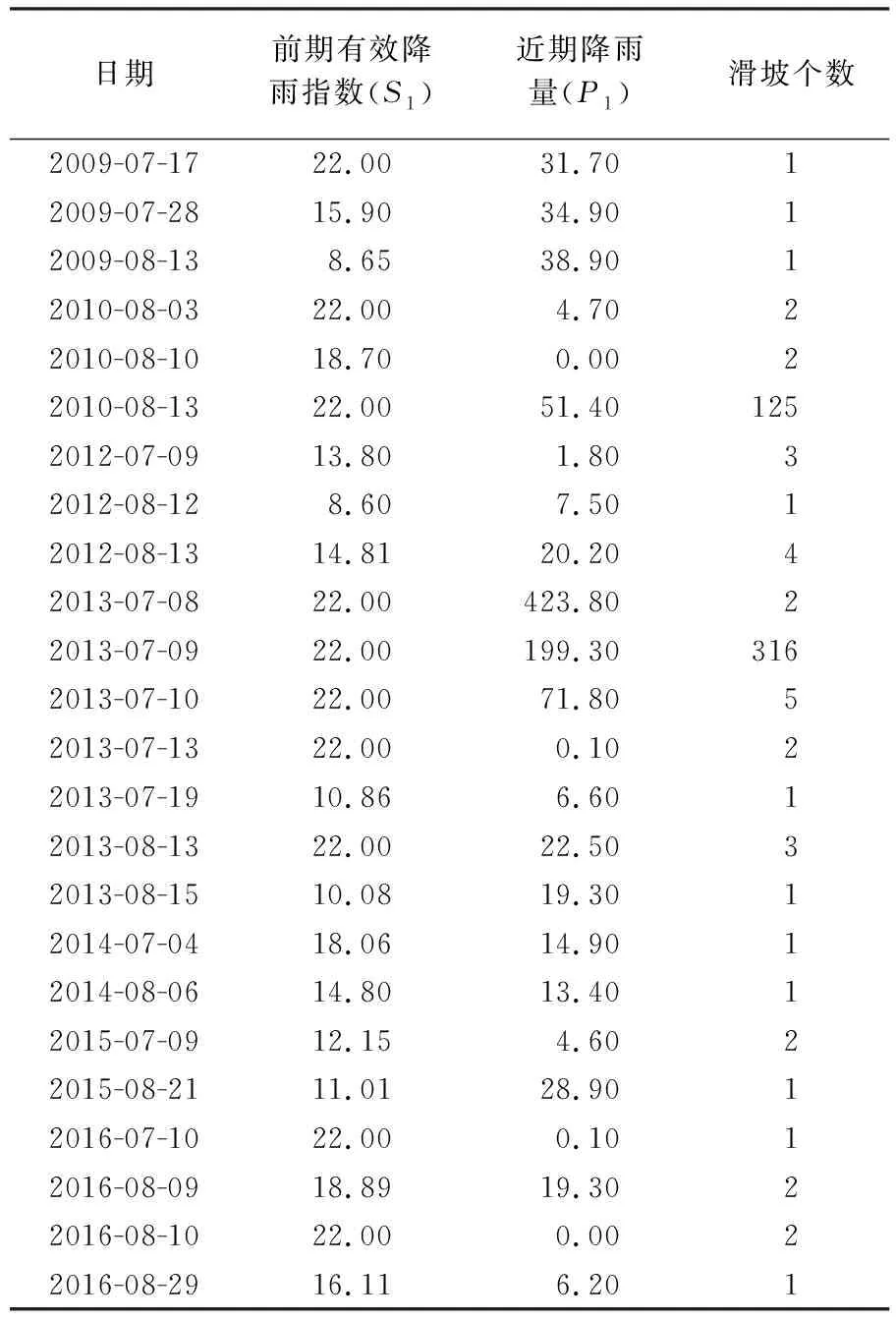
表1 滑坡事件的近期降雨量及前期有效降雨指数统计表(近期与前期的分界为1 d)

3.2.2 近期与前期的分界为3 d

当用事件前3 d(包括事件当天)的累积降雨量作为近期降雨量，3 d之前的前期有效降雨指数来表征前期土壤湿度情况时，通过评估不同阈值表达式的滑坡预测能力，得到的最优阈值表达式为

P3=4.7-0.01S3

(11)

P3=6.9-0.37S3

(12)

式中，P3为事件前3 d的累积降雨量，单位为mm；S3为3 d之前的前期有效降雨指数，单位为mm。

式(11)所示的阈值表达式是在评价指标欧几里得距离最小时得到的，称为模型3，而式(12)所示的阈值表达式是在限制命中率为1的情况下，误报率最低时得到的，称为模型4。图8展示了这两种模型对应的阈值曲线及相关事件的分布，其中滑坡事件的近期降雨量及前期有效降雨指数见表2。由表2可知，滑坡发生前3 d的降雨量最小为4 mm，最大可达694.9 mm，相比于表1中滑坡发生当天的降雨量，滑坡发生前3 d的降雨量都有所提高，说明滑坡发生的前2 d都伴随有降雨。3 d前的前期有效降雨指数变化范围为8.94～22 mm，与表1中1 d前的前期有效降雨指数的变化范围相似，但对于3 d前的前期有效降雨指数，其取值为22 mm，即前期土壤湿度为饱和状态的事件仅有6个，说明滑坡发生3 d前的土壤湿度状态以不饱和的居多。主要是因为即使3 d前的土壤没有处于饱和状态，从近期降雨量的分布可知，接下来的3 d都有降雨发生，这些降雨会进一步使斜坡土体处于饱和状态，为滑坡的发生创造条件。

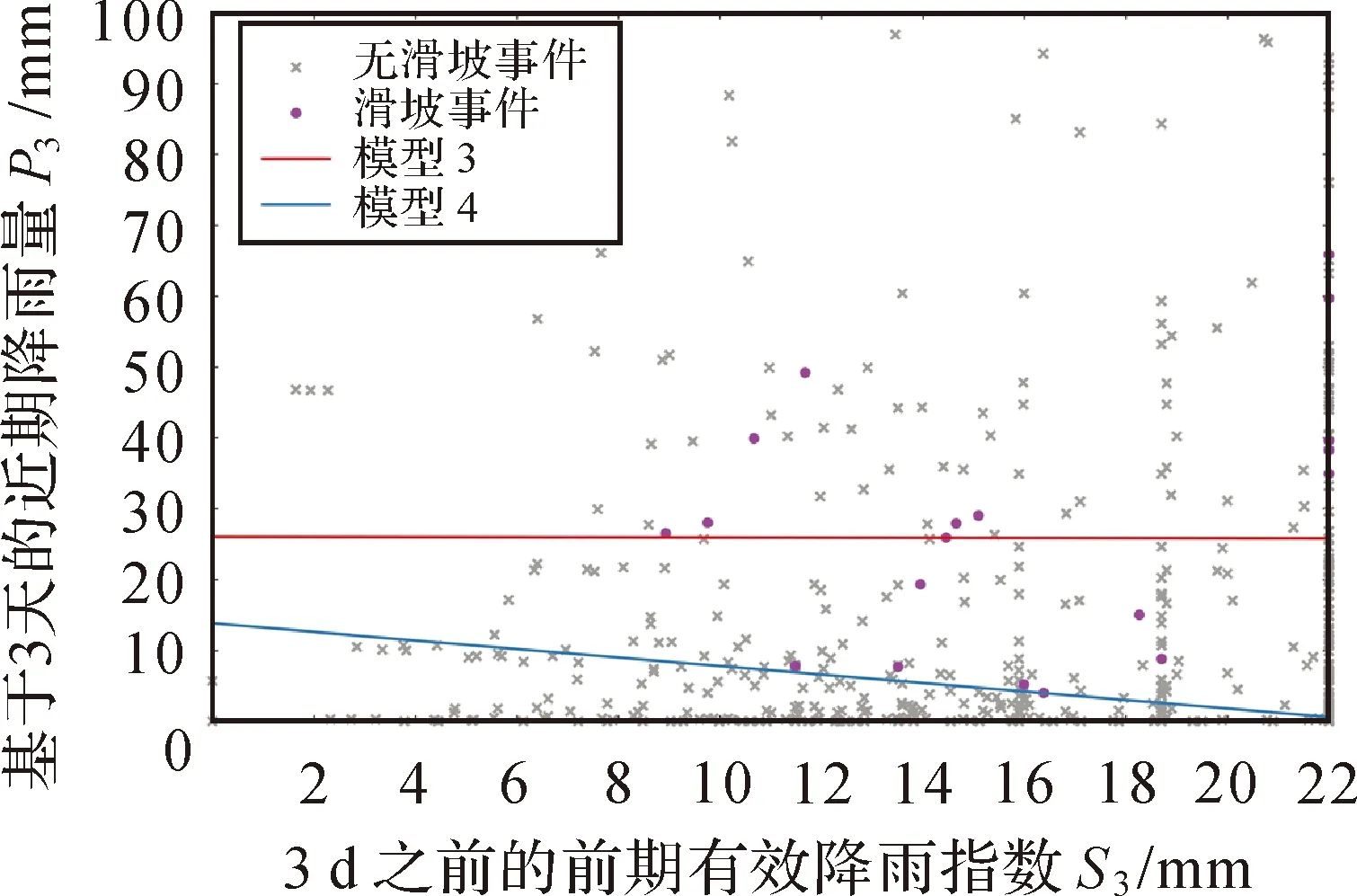
图8 基于近期降雨和前期有效降雨指数的水文-气象阈值曲线(近期与前期的分界为3 d)Fig.8 Hydro-meteorological threshold curve based on the recent cumulated rainfall and API (The boundary between recent period and antecedent period is three days)

由图8可以看出，对于模型3的阈值曲线，当前期有效降雨指数为0 mm时，如果近3 d的降雨量超高26 mm，则认为滑坡有可能发生；而对于模型4的阈值曲线，当前期有效降雨指数为0 mm时，如果近3 d的降雨量超高13.8 mm，认为滑坡有可能发生。

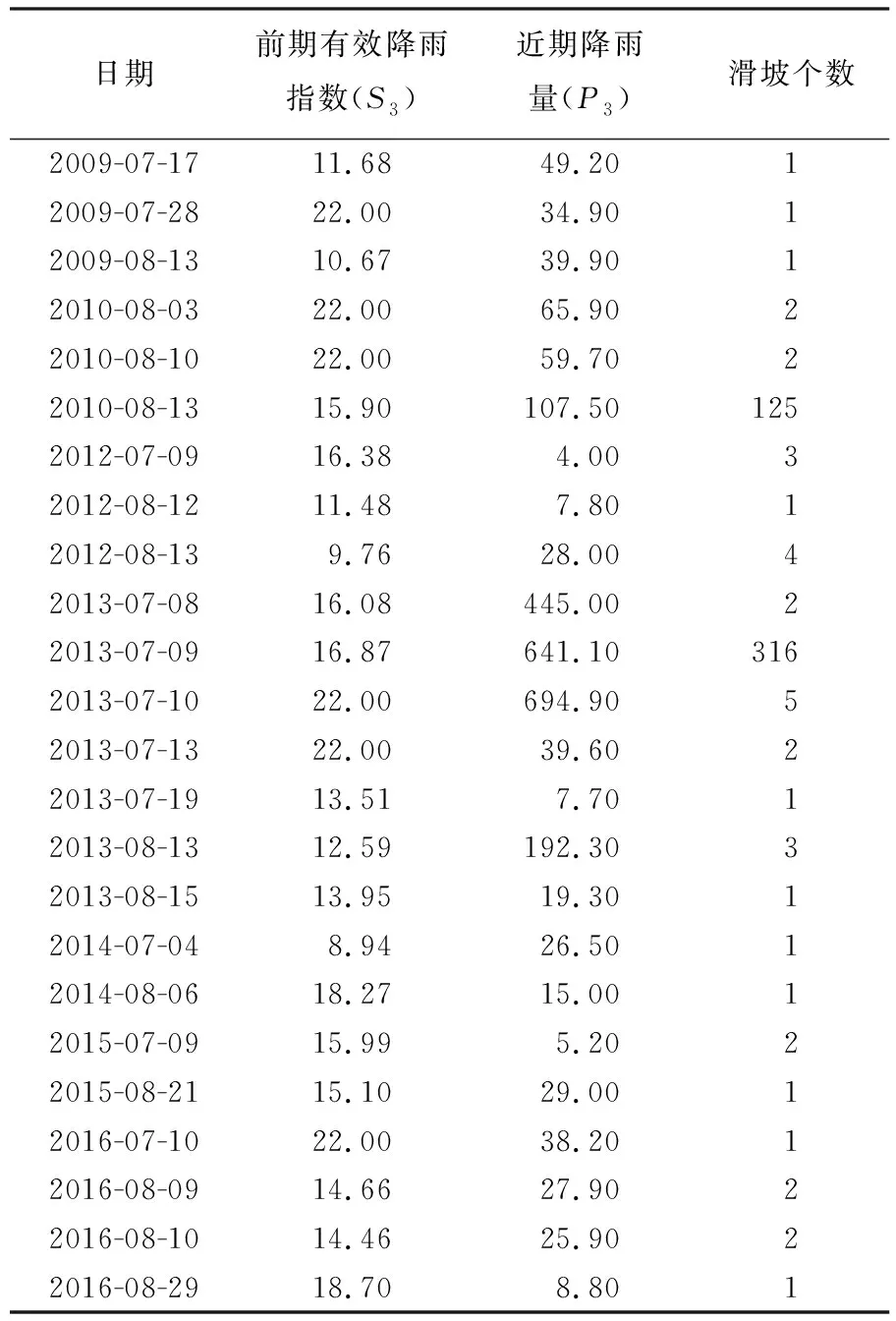
表2 滑坡事件的近期降雨量及前期有效降雨指数统计表(近期与前期的分界为3 d)

3.3 滑坡预测精度

表3和表4分别列出了上述4个水文-气象阈值模型的预测结果。在评估上述4个模型的滑坡预测精度时，2009—2016年的7、8月期间的每一天都被当作一个事件，因此共有496个事件，其中有24个事件为滑坡事件。由表3可知，当近期与前期的分界为1 d时，由欧几里得距离最优确定的模型1得到的命中率为0.79，误报率为0.26，此时该预测结果距离最优点的距离即欧几里得距离为0.34。在限制命中率为1的情况下，由误报率最优确定的模型2得到的命中率为1，误报率为0.56，此时欧几里得距离为0.56。由表4可知，当近期与前期的分界为3 d时，模型3的预测结果命中率为0.71，误报率为0.25，此时欧几里得距离为0.38；而模型4的预测结果命中率为1，误报率为0.58，此时欧几里得距离为0.58。

对比表3和表4可知，当近期与前期的分界为1 d时预测结果较好，因此认为适用于试验区域的近期与前期的分界为1 d，即在确定阈值表达式时，用事件当天的降雨量作为近期降雨量，当天之前的前期有效降雨指数来表征前期土壤湿度情况。在确定了近期与前期的分界后，表3中模型1和模型2的选择取决于实际情况，因为这两种模型各有优劣，模型1在牺牲命中率的同时降低了误报率，而模型2在满足命中率为1的情况下增加了误报率。在实际应用中，如果滑坡漏报造成的影响较大时，应选择模型2来尽量避免漏报；如果滑坡漏报造成的影响不是很大时，可以考虑选用模型1来尽可能地降低误报造成的影响。

表3 水文-气象阈值模型的预测结果(近期与前期的分界为1 d)

表4 水文-气象阈值模型的预测结果(近期与前期的分界为3 d)

4 结 论

本文构建了基于水文-气象阈值的区域降雨型滑坡预测模型，其中前期土壤湿度情况由改进的前期有效降雨指数刻画，近期降雨情况由最近的累积降雨量表示。为验证所构建模型的有效性，本文将上述模型运用于都江堰地区的降雨型滑坡预测。试验结果表明，相比于近期与前期分界为3 d的情况，当近期与前期的分界为1 d时，水文-气象阈值的滑坡预测表现更好，即用事件当天的降雨量刻画近期降情况，当天之前的前期有效降雨指数表征前期土壤湿度情况。对于该模型，以欧几里得距离最小确定的水文-气象阈值，命中率为0.79，误报率为0.26；在限制命中率为1的情况下，由误报率最小确定的水文-气象阈值，命中率为1，误报率为0.56。这两个评价指标确定的水文-气象阈值模型各有优劣，模型的选择应考虑滑坡漏报和误报造成的影响及对漏报和误报事件的可接受程度。

相比于传统降雨阈值模型，本文构建的水文-气象阈值模型可充分考虑前期土壤湿度和近期降雨在降雨型滑坡发生过程中的共同作用，即前期土壤湿度通过影响孔隙水压力决定了斜坡的稳定性，降雨作为诱发因素可直接导致滑坡的发生。另一方面，利用改进的前期有效降雨指数表征前期土壤湿度情况，可有效减少模型对数据的需求，有利于水文-气象阈值在区域降雨型滑坡预测中的应用，尤其是在数据匮乏区域的推广。

本文以都江堰地区为例验证了所建水文-气象阈值模型在区域降雨型滑坡预测中的有效性，但是本文研究所涉及的滑坡数据和水文气象数据都比较有限，在将来的研究中，仍需基于更多的试验区域，利用更完整的数据来验证水文-气象阈值模型的滑坡预测能力，以期进一步完善和改进考虑前期土壤湿度的区域降雨型滑坡预测方法。