时序InSAR滑坡形变监测与预测的N-BEATS深度学习法——以新铺滑坡为例

郭澳庆，胡 俊，郑万基，桂 容，杜志贵，朱 武，贺乐和

1. 中南大学地球科学与信息物理学院，湖南 长沙 410083; 2. 长沙天仪空间科技研究院有限公司，湖南 长沙 410205; 3. 长安大学地质工程与测绘学院，陕西 西安 710054

滑坡是指在斜坡上的岩体土体，当受流水冲刷、降雨冲刷、地下水运动及地震等因素的影响时，在重力作用下失稳而沿斜坡向下滑动的自然现象[1]。山体滑坡通常发生突然，破坏力巨大，经常会造成重大的生命安全事故和财产损失。因此，滑坡形变的全面监测和中短期实时预测技术的进步对防灾救灾来说更具有突出的现实意义。

滑坡形变监测和预测方面的研究在目前来说仍是一大热点。合成孔径雷达干涉测量技术(interferometric synthetic aperture radar,InSAR)[2-5]以其非接触式的测量功能获得卫星目所能及之处的面状形变数据，相较于利用全球导航卫星系统数据(Global Navigation Satellite System,GNSS)和传统地面监测数据进行滑坡预测而言，InSAR技术能够提供无接触式低成本的面域测量，既降低了GNSS接收站和传统地面监测仪器的安装维护成本，又能够获得滑坡形变区更加全面的面域形变状态，成为了滑坡形变的主流监测手段之一[6-9]。

由于滑坡形变序列受到机理复杂和种类繁多的变量因子的影响[10]，其波动呈现出非线性和不确定性而导致滑坡预测问题较难解决，在基于InSAR技术的滑坡形变预测方面的研究更是屈指可数。因此，寻找到更加适合于InSAR形变数据分析且能够准确有效完成滑坡形变预测任务的方法和技术是解决问题的方向。

目前，针对InSAR滑坡形变数据分析的方法可以被分为两类：模型驱动型和数据驱动型[11]。模型驱动型的代表有概率积分法、卡尔曼滤波、灰色系统理论模型、逆速法线性逼近、非线性最小二乘及有限元方法模拟等，依靠形变数据及丰富的岩土信息能够获得高精度且可靠的地面形变预测结果。但实际上，这类数值模拟方法受测量误差、环境噪声及建模假设等因素的干扰效果明显，表现为模型抗差性能低，迁移应用能力弱，各类岩土信息的获取也消耗巨大的人力物力资源，大多数中小型工程难以承担设备维护及灾害预警的成本。数据驱动是当前很热门的数据分析方法，它利用数据本身的信息和特定任务的实际需要能够创造出新的计算模型；在各种实际情况下使模型贴合特定的数据，用客观和清晰的数据将分析过程化繁为简，因而无须受限于现有模型；相较于模型驱动更具有从统计观点来解决实际问题的特色。数据驱动型分析方法随着机器学习的出现而逐渐被研究者们接受和青睐，深度学习则是一种既能智能模拟人类大脑又具有强大计算和数值分析能力的工具，例如长短期记忆(long short-term memory，LSTM)网络模型[12]在大范围地表沉降形变预测的应用中大放异彩。神经网络底层扩展分析(neural basis expansion analysis，N-BEATS)网络模型[13]是一种深度神经网络，是数据驱动模型进行时间序列数据分析的代表。它在不同领域的大型时间序列数据分析中都展现出了先进的预测能力，如M3、M4和TOURISM竞赛数据集。常用时序形变预测方法见表1。

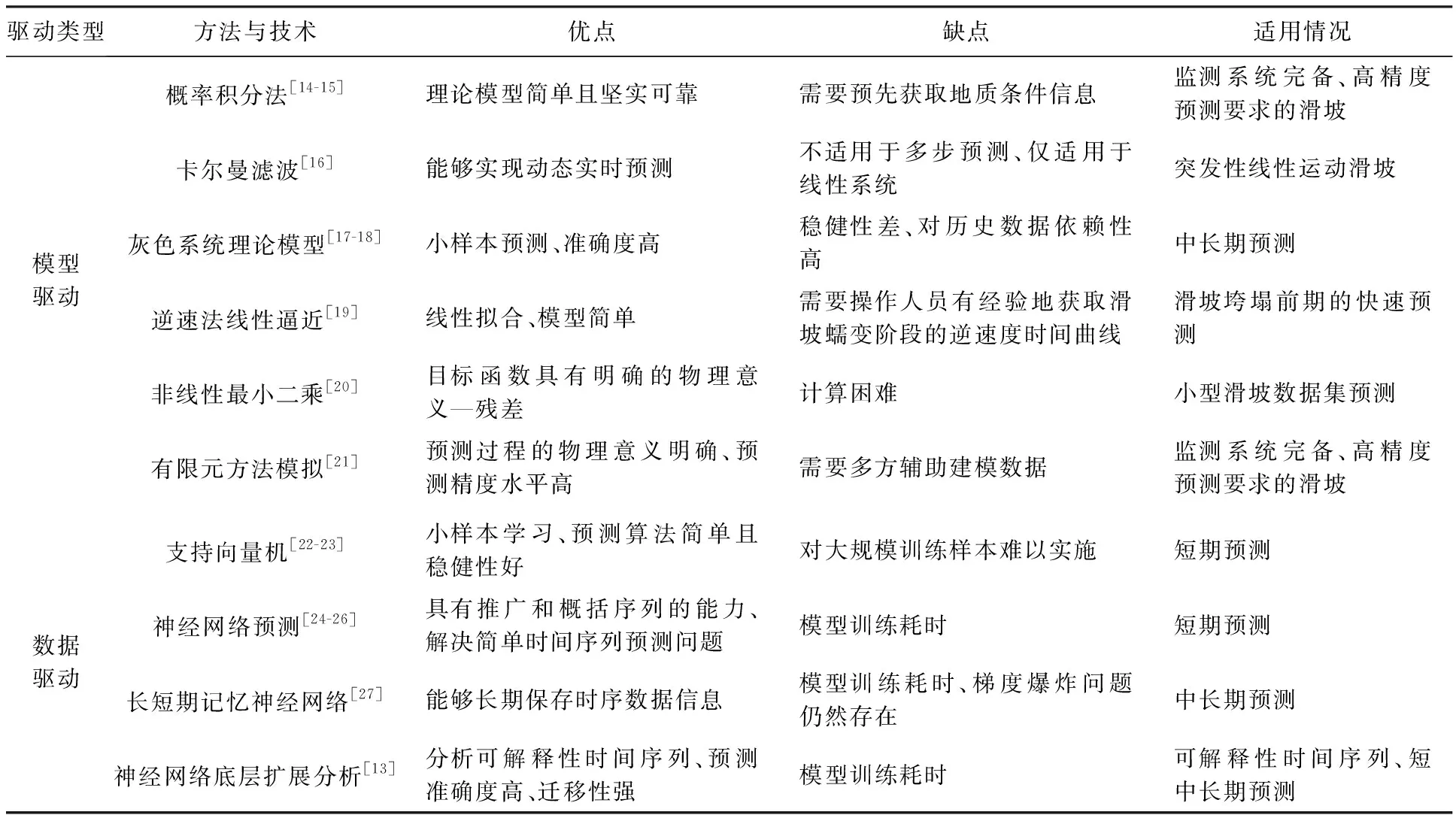
表1 地质灾害时序数据预测方法优劣一览

本文利用时序InSAR获取形变监测结果，结合N-BEATS神经网络开展滑坡形变预测工作，发挥N-BEATS模型强大的时间序列数据自动分析，以及高精度、高可靠性和具有一定抗差能力的预测优势，将研究目标定位于中短期滑坡小数据集，应用于三峡库区的Ⅰ级滑坡—新铺滑坡，把这种有效的深度学习时间序列预测模型应用于解决基于时序InSAR形变观测的中短期滑坡预测难题。

1 基于N-BEATS网络和时序InSAR的滑坡形变预测方法

常规测量方法在理论建设阶段都有着较为完美的效果，但在实际的工程实践中却难以克服一些特殊的环境因素，例如滑坡发生区域的茂密植被会遮挡导航定位信号，导致相位信息断链使GNSS技术时而失效。地下地面常规测量方法一次建设投入成本巨大，二次建设及维护成本在滑坡发生之时被毁坏后更是不知凡几。InSAR技术能够高精度、少干扰获得面状形变数据，更适合大范围滑坡区域的全面监测；而具有强大学习能力、有效探索时序变化规律的深度学习模型N-BEATS更适合复杂非线性滑坡形变预测。

本文基于深度学习和时序InSAR的滑坡形变预测任务主要分为3个步骤：滑坡形变监测获得历史数据、组织数据结构和时间序列数据分析向前预测。首先，在SAR监测获得时序形变影像后经过时序TCP-InSAR技术[28]进行处理，该方法能够克服在InSAR数据分析过程中，由于相位解缠处理不当而带来的误差影响的问题，得到滑坡区的形变速率。然后，对时序滑坡形变影像数据进行选择和重新组织，找出滑坡危险区特征点，并将特征点数据重新组织成为一维时间序列，并对一维时间序列数据进行时序分解，分析其变化特征，确定预测任务数据集的输入输出窗口设置策略，以防损失数据特征。最后，将时间序列按照比例划分为训练集和测试集，训练N-BEATS网络模型并测试模型训练结果，完成时序预测。本文的主要工作是预测任务数据集设置策略的探究及N-BEATS时序预测模型建立、训练和预测两个部分。

1.1 预测任务数据集设置策略

目前，基于InSAR技术的滑坡形变预测还停留在单点时序预测阶段，对于深度学习来说，需要人为进行优化控制的主要是超参数的选择，除此之外还有数据组织形式的设置策略。由于硬件设备的计算性能有限，因此一次训练的输入数据不宜过大，也就是无法将全部历史数据作为单次输入进行操作，那么这就需要人工根据经验选取部分具有充分代表性的数据作为输入的训练数据。研究者们通过丰富的试验和经验发现，不同的数据组织形式对数据预测效果和训练能力都有很大的影响。

在输入窗口大小的设置中，针对具有周期性特征的时间序列，其输入窗口的长度需要达到能够体现真实周期的数据长度，以免丢失周期信息；针对具有突发性变化的时间序列，其输入窗口的长度需要充分包括突发性状况的整个时序变化趋势；针对包括其他非线性特征的时间序列，也需要获取相应的具有充分代表性的数据长度。在输出窗口大小的设置中，需要在满足深度学习预测结果正确的前提下同时兼顾真实预测时间频率及时间延展需求。

对上述数据进行规律性分析的方法在时间序列分析领域有很多，本文主要采取的策略是对数据进行简单时序分解，基于Loess的季节趋势分解方法(seasonal-trend decomposition procedure based on Loess,STL)是一种能够将存在可解释性特征的时间序列分解成为趋势因子、季节因子及随机因子，适用于本文所针对的大型缓慢滑坡形变应用。

1.2 N-BEATS网络模型架构

N-BEATS网络是由若干感知机单元组成，依据一定策略搭建成的深度神经网络。该网络结构具有两个作用：①模拟，对原始时间序列数据的特征进行提取并模拟；②预测，从时间维度延续模拟出的序列数据特征，从而完成预测。

N-BEATS网络模型的搭建策略是从时间序列分解中获得的灵感，因此该模型的优势不仅在于能够获得准确性高的预测结果，其预测结果也具有类似于STL方法的对趋势性、季节性等时序变化的可解释能力。其框架结构如图1所示，网络一次训练的输入即为设定窗口大小的历史数据序列，使序列数据依次经过M个堆栈来分别识别数据的不同特征，每个堆栈中存在若干块区，块区之间通过残差模块进行衔接，每个块区中又含有几个计算神经元。

1.2.1 N-BEATS网络架构的工作思路

(1) 区块层学习时间序列演化模式。首先，使原始时间序列数据经过4层全连接层；然后，经过线性投影层后进行线性变换分别生成向前预测系数和向后预测系数；最后，使向前预测系数和向后预测系数分别通过偏置层输出向前预测和向后预测结果，如图1(a)所示。向前预测结果是沿时间序列发展方向的预测未来序列走向的结果。向后预测结果是恢复出的历史时间序列，用于信号分离。因此，块区中输入为原始序列数据；输出为向前预测和向后预测结果。

(2) 堆栈层分解剩余时间序列特征。每一个块区的输出都是其的向前预测和向后预测结果，如图1(b)所示。向前预测结果被整合起来成为该堆栈的输出结果，向后预测结果通过残差的形式存在于块区之间，并将块区衔接起来，更有利于梯度的反向传播也使得下一个块区的预测工作更加简便。因此，本堆栈中的输入为各块区向前预测和向后预测结果；输出为这部分中经过整合得到的向前预测结果。

(3) 整合时间序列特征预测分量。各部分堆栈的输出最终被整合了起来，叠加各个堆栈获得的特征分量就能够得到总体预测结果，即预测数据的序列，如图1(c)所示。

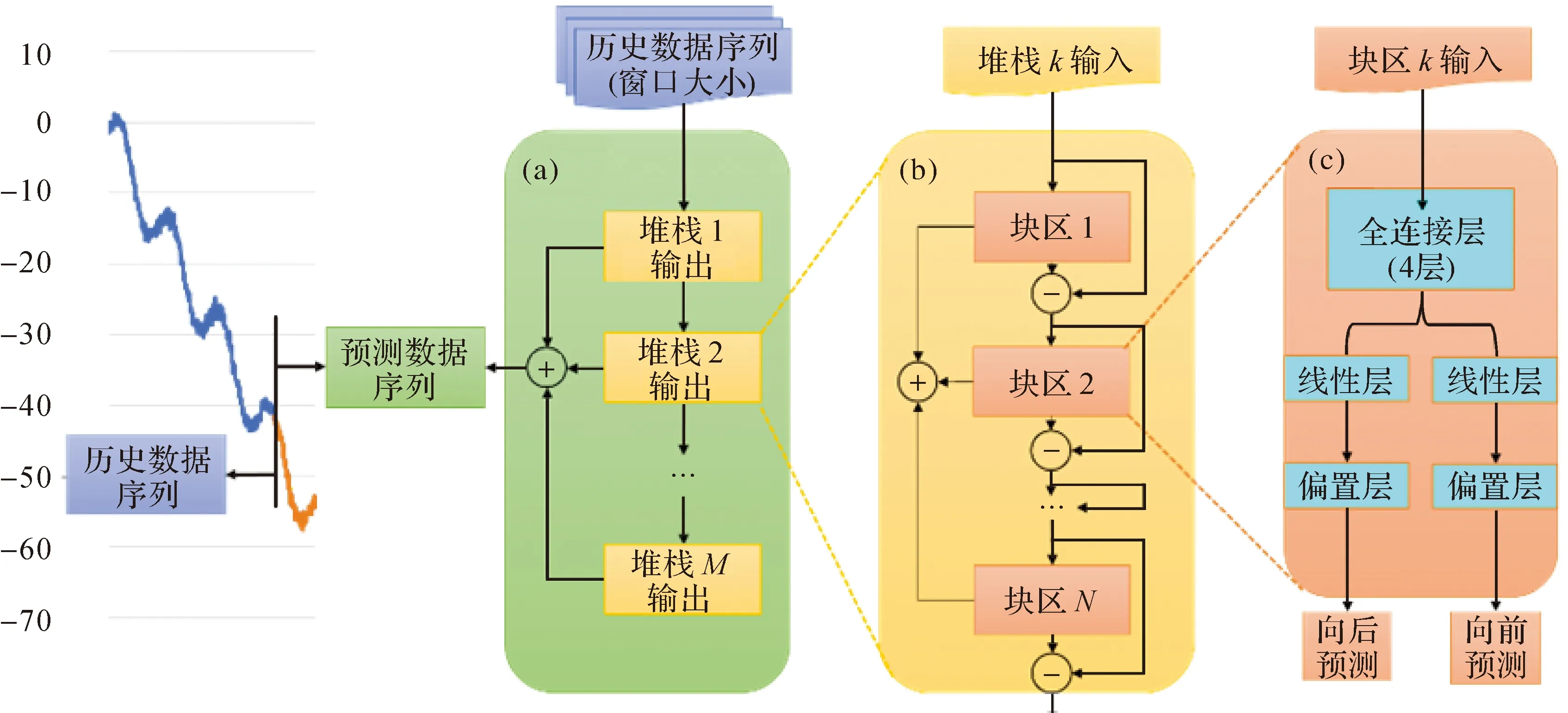
图1 N-BEATS网络模型架构Fig.1 N-BEATS network model architecture

1.2.2 N-BEATS网络架构优势

该网络架构能够实现对趋势性、季节性等时序变化的解释，主要核心在于对不同堆栈中的神经单元建议不同的线性层和偏置层，架构中主要的优势即可解释性，它体现在趋势项和周期项两堆栈中。

(1) 趋势模型。趋势模型的特征通常是呈线性单调递增或单调递减，并且其变化应是较为缓慢的。因此在趋势项堆栈中(c)部分的线性层和偏置层被设置为

y=T·x

(1)

式中，T=[1,t1,t2,…,tp]，p为一个小值，用于控制线性单调递增或递减行为的速度，使趋势缓慢变化；t为时间向量；x为该块区中线性层和偏置层的输入；y为该块区中线性层和偏置层的输出。

(2) 周期模型。周期模型通常被认为是循环往复的，有涨落规律的变化。因此在周期项堆栈中(c)部分的线性层和偏置层被设置为傅里叶级数形式

y=S·x

(2)

(3)

式中，t为时间序列向量；H为向前预测的窗口长度；x为该块区中线性层和偏置层的输入；y为该块区中线性层和偏置层的输出。

2 研究区域与数据源介绍

2.1 研究区域介绍

新铺滑坡区是位于三峡库区的安坪乡新铺村境内的Ⅰ级地质灾害区，研究区位置示意如图2所示。图2(a)、(b)显示了新铺滑坡研究区在重庆市及其与长江的相对位置，图2(c)显示了滑坡体的具体分布情况。滑坡易发区地处长江右岸。新铺滑坡由于其多期活动，整个斜坡的坡面形成了多级台地地貌，滑坡从上至下共有3处，分别是大坪滑坡、上二台滑坡和下二台滑坡。

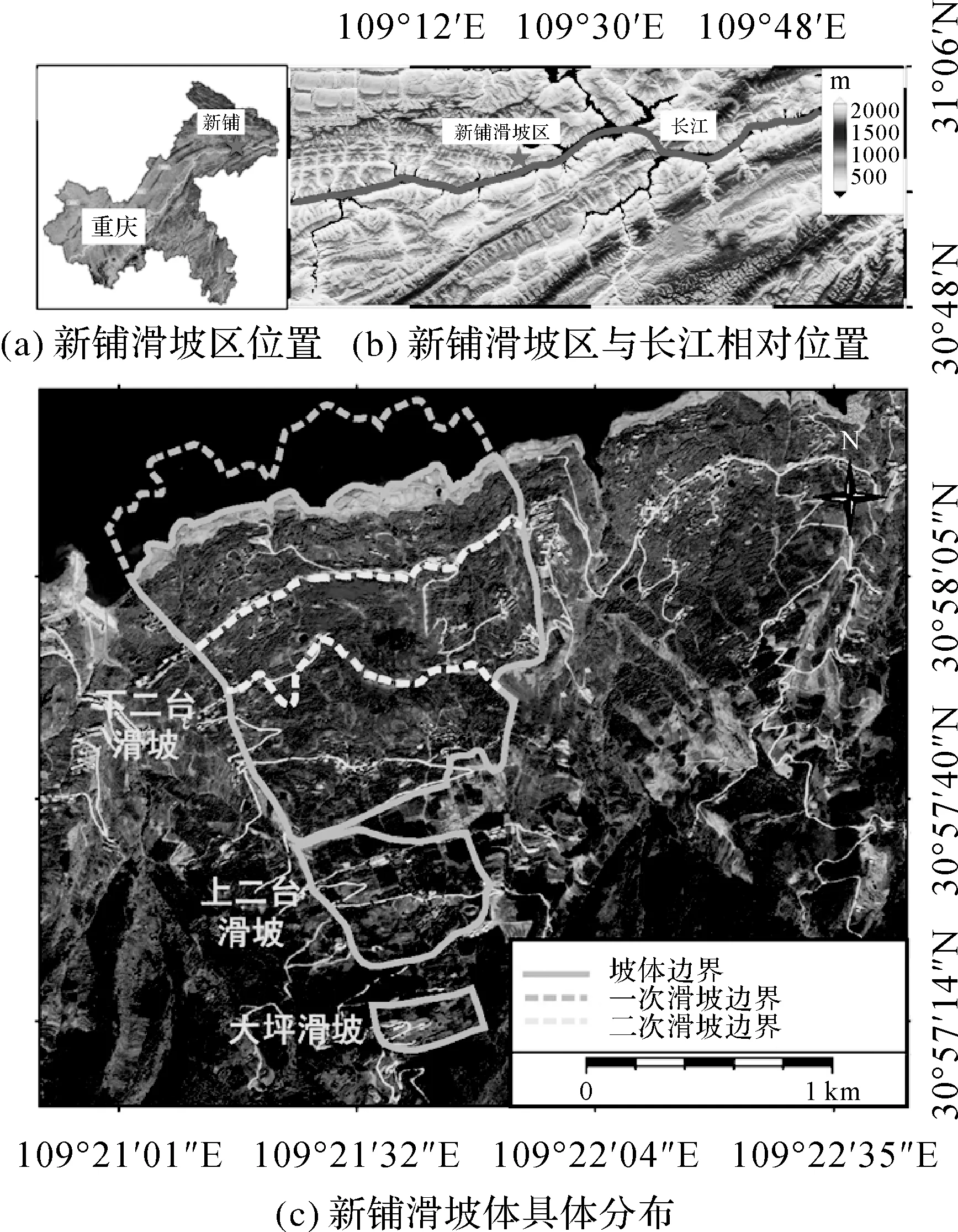
图2 新铺滑坡研究区Fig.2 Xinpu landslide research area

大坪滑坡区域的岩体呈现出裂隙发育，倾角为20°～28°，该区域的变形破坏特征并不明显，为顺层基岩滑坡破坏模式。

上二台滑坡区域整体土体的厚度变化较大，在降雨入渗的影响下，土体会沿着滑面产生缓慢的变形破坏，形成推移式浅层土体滑坡。

下二台滑坡区域由于前缘的长江河谷创造了较好的临空条件，但受到地形、降水、长江水位波动及掏蚀等的作用，表面松散物质沿坡面发生牵引式滑移破坏，最下层至江边地段受长江河水涨落和冲刷作用产生蠕滑变形。

该区域滑坡评估结果显示变形破坏模式为顺层基岩滑坡破坏模式、推移式浅层土体滑坡破坏模式和牵引式浅层土体滑坡破坏模式，非常适合采用InSAR技术进行滑坡变形的长期监测。因此本文试验以重庆市奉节县安坪乡新铺村的新铺滑坡作为研究对象。

2.2 数据源介绍

本文试验针对新铺滑坡形变的监测预报收集的原始合成孔径雷达(synthetic aperture radar,SAR)影像取自哨兵一号(Sentinel-1)卫星星座。该星座由1A和1B两颗星组成，每单个卫星12 d可覆盖地球一次，其上的C波段合成孔径雷达能够全天时全天候地提供对地观测影像。

Sentinel-1A地球监测卫星于2014年发射并试运行，Sentinel-1B地球监测卫星于2016年发射。目前，Sentinel-1数据和影像已经能够提供一系列的运营服务，例如海洋测绘、地面运动风险监测、森林制图，以及地籍管理和测绘等众多应用。

本文试验获取了由Sentinel-1A提供的时间序列SAR数据，获取了由2016年8月1日—2020年10月15日时间间隔为12 d的124幅SAR影像，数据相关信息见表2。

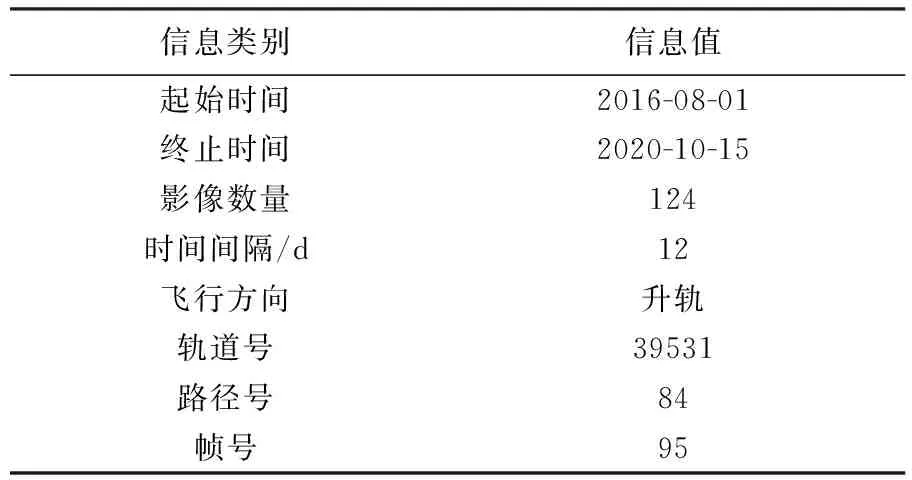
表2 Sentinel-1A时序SAR数据信息

3 新铺滑坡形变预测试验

3.1 N-BEATS网络模型设置

N-BEATS模型预测数据的结构由窗口大小决定，根据窗口大小来决定由向后的k个历史时刻作为输入序列，向前预测m个未来时刻的输出结果，本文试验需要预先根据时序数据特征设置窗口大小，即输入数据窗口为x1,x2,…,xk，标签值为xk+1,xk+2,…,xk+m，以此类推至最后一个窗口的输入数据为xn-9,xn-8,…,xn，标签值为xn+1,xn+2,…,xn+m，其中n为总数据长度。数据需要满足等间隔要求，若存在缺失数据的情况则需要通过插值方法补全。

试验设置3个堆栈，分别处理季节性、趋势性及其他形变信号，每堆栈设置块区数为2，每个块区中设置4层全连接层，其中隐藏层单元均为64个，随全连接层之后的线性层和偏置层参数维度设置分别为[2,2,3](季节堆栈模型、趋势堆栈模型和其他形变堆栈模型)。N-BEATS滑坡预测网络模型结构如图3所示。模型训练过程采用小批量为16的mini-batch梯度下降，训练所有样本共400次。

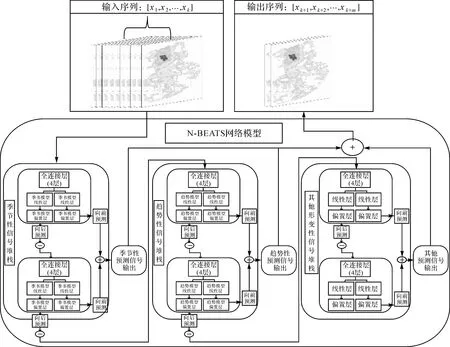
图3 N-BEATS滑坡预测网络模型结构Fig.3 N-BEATS landslide prediction network model structure

损失函数用于估量模型的预测值与标签值的差异程度，深度学习的目标是利用优化器来最小化损失函数的计算值，使得模型预测值与标签值的差异缩小至最小，从而训练得到最好的模型，本文中N-BEATS网络模型所使用到的损失函数是平均绝对误差损失函数(mean absolute error loss，MAELoss)，平均绝对误差描述的是模型预测值与样本标签值之间距离的平均值。优化器为Adam，学习率设置为0.002。Adam是通过计算梯度的一阶矩估计和二阶矩估计来为不同参数设计独立的自适应学习率的一种优化算法。在实践中相较于其他的随机优化算法具有更好的性能，以上超参数设置见表3，本文中使用的网络超参数应用了N-BEATS网络模型的推荐参数进行经验性多次实验后微调获得。

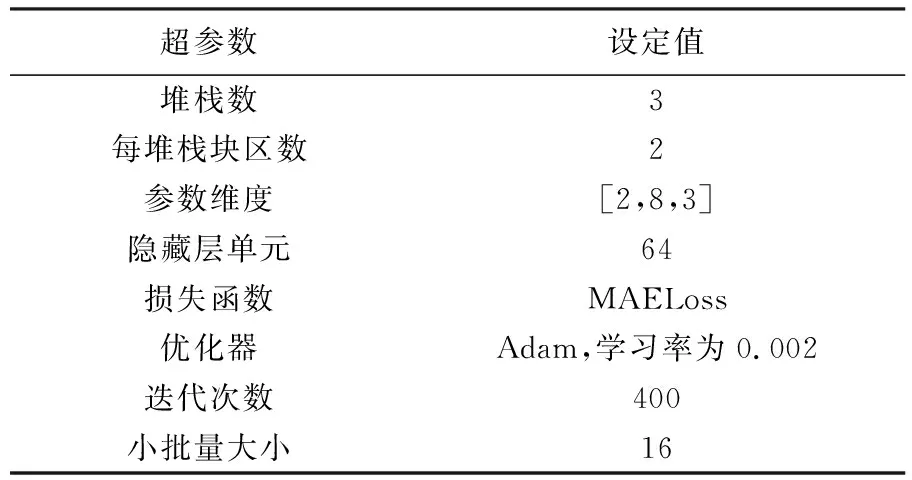
表3 N-BEATS网络模型设置一览表

3.2 预测任务数据集设置

为探究预测数据集输入输出窗口设置对预测效果的影响，本文采取对数据进行简单时序分解的策略，利用STL算法将研究目标时间序列分解成为趋势因子、季节因子及随机因子，分解后P点的序列特征如图4所示，图4(a)、(b)分别为P点时间序列分解特征及P点点位示意。可见该滑坡时间序列数据成分大致为84%的趋势项、8%的周期项及8%的不确定因子。数据表现出持续下降的走势(远离卫星方向)，并存在以年为周期的季节性形变，除此之外还在4年间有过两次突发性形变发生，但该突发性影响所带来的形变并不是很大，未超过1 cm。

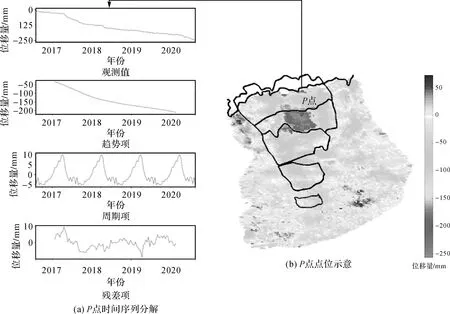
图4 形变时间序列分解特征Fig.4 Deformation time series decomposition feature diagram

上述时序分解成分中，趋势项成分在整个时间序列中的特性表现为稳定不变，无须在输入输出窗口大小的设置中考虑该成分；不确定成分呈现无规律发展的变化形式，无法在设置窗口时照顾到该成分的变化特征；周期性成分在整个时间序列中表现出明显的局部性特征，因此该成分是输入输出窗口大小设置的重要依据，若要求网络模型学习到一个整周期的形变趋势，则周期性成分也是限制使用者需要提供训练样本最低数量的重要依据，若对形变趋势的周期性形变捕捉能力不做要求则无须满足此数量条件。以年为周期的周期性成分在一年的时间序列中的长度约为30，考虑到总样本长度为124，为保证训练数据的样本集丰富的同时兼顾序列的周期性特征，分别将输入窗口设置为[4,6,…,18,20]，输出窗口设置为[1,2,…,5,6]，对这54种组合进行训练并测试得到预测结果如图5所示，并对预测结果计算均方根误差见表4，可见随着输入和输出窗口的增大，预测结果的准确度在逐渐降低。输入窗口越大，表明在模型训练时被考虑到的周期性成分更加完备，但由于同时缩小了数据集而使得模型的学习数据减少，训练效果反而降低；输出窗口越大，表明期待预测到未来未知时间序列数据的长度越长，即更加“贪心”，则也相应地会付出预测精度下降的代价。

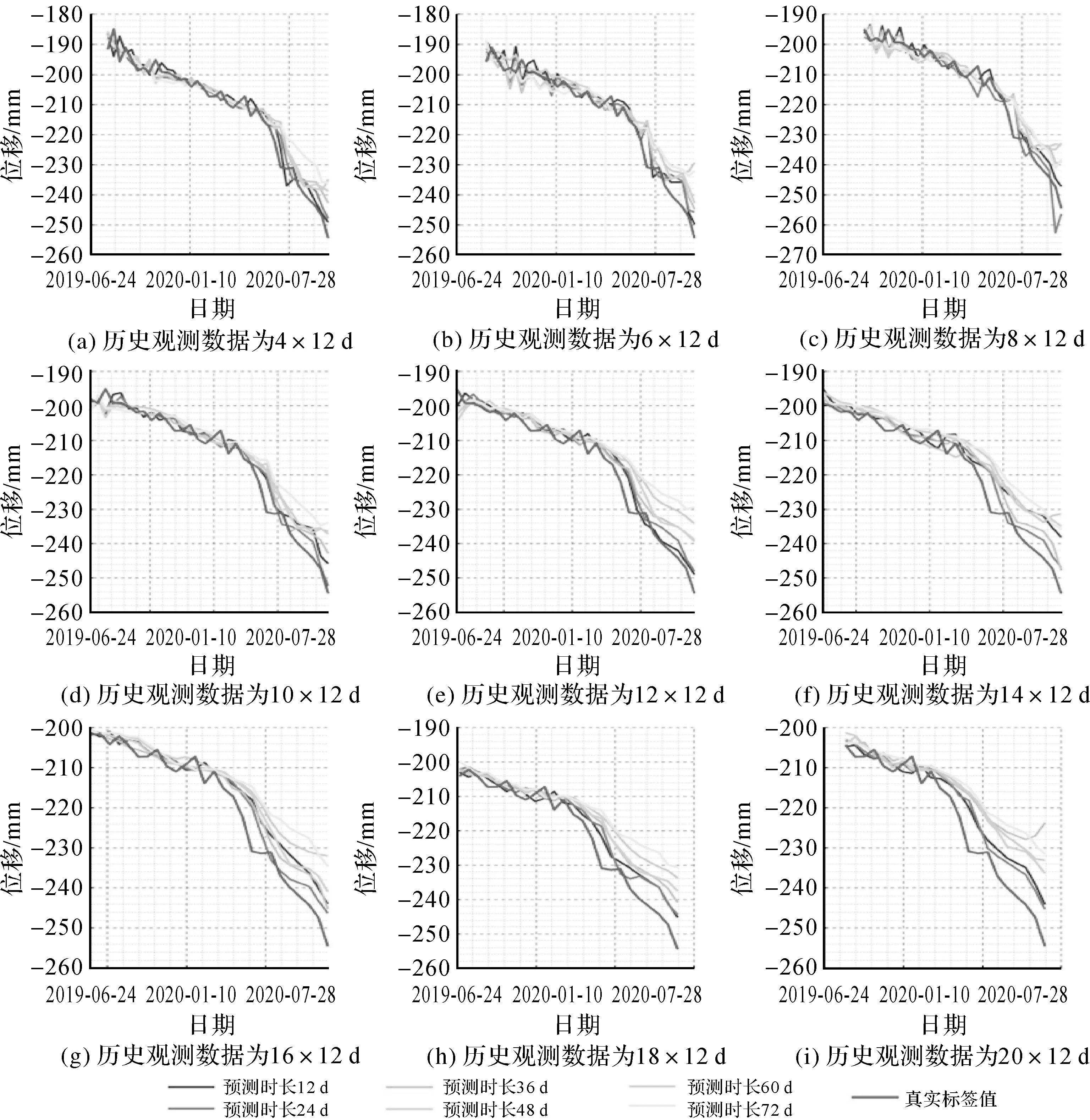
图5 54种输入输出窗口组合的预测结果Fig.5 Prediction results of 54 combinations of input and output windows

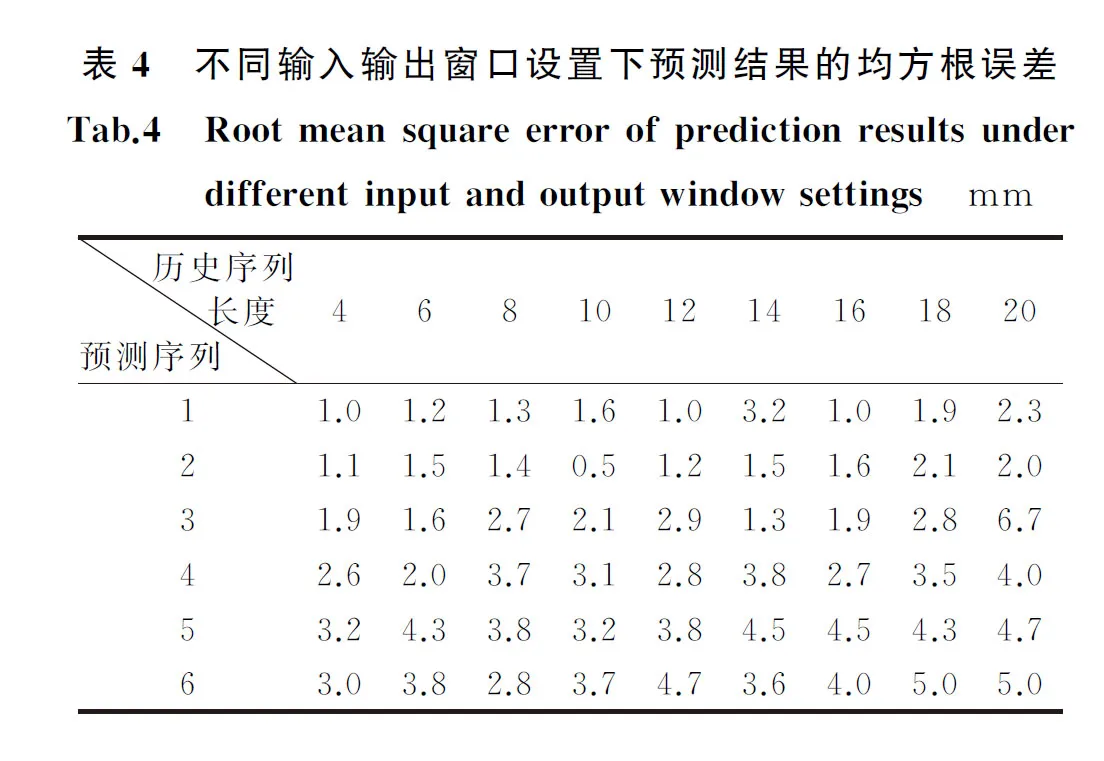
对比之下，本文选择了输入输出窗口为[10,2]的数据集组织模式，该模式能够在满足预测中短期滑坡形变时长的条件下达到最高精度要求。

3.3 滑坡预测结果

经过TCP-InSAR技术处理后获得形变区位移图，选取影像中整体相干性大于0.8的5148个样本点，将其展开并重组为时间序列数据。将数据集按照2∶1比例划分为训练集数据和测试集数据，为保证预测效果表现力，未将测试数据集打乱顺序。根据模型运行的实际情况发现窗口大小为[5,1]，设置参数维度为[2,8,3]，迭代次数在300时已经能够稳定地呈现出较为理想的预测结果。

A、B、C3点位置在图6中体现，其形变趋势如图7所示，蓝色曲线为数据样本点的历史观测值，橙红色曲线为样本点未来趋势的真实标签值，黄色曲线为N-BEATS网络模型的预测结果。可见，数据预测结果遵循历史数据的走向，说明了预测的正确性；放大预测结果与真实标签值的细节，可以看出预测结果与真实标签高度吻合，说明了该方法用于新铺滑坡区的长期时间序列预测的有效性。

图6 新铺滑坡区沉降区特征点位置Fig.6 Location of feature points in settlement area of Xinpu landslide area

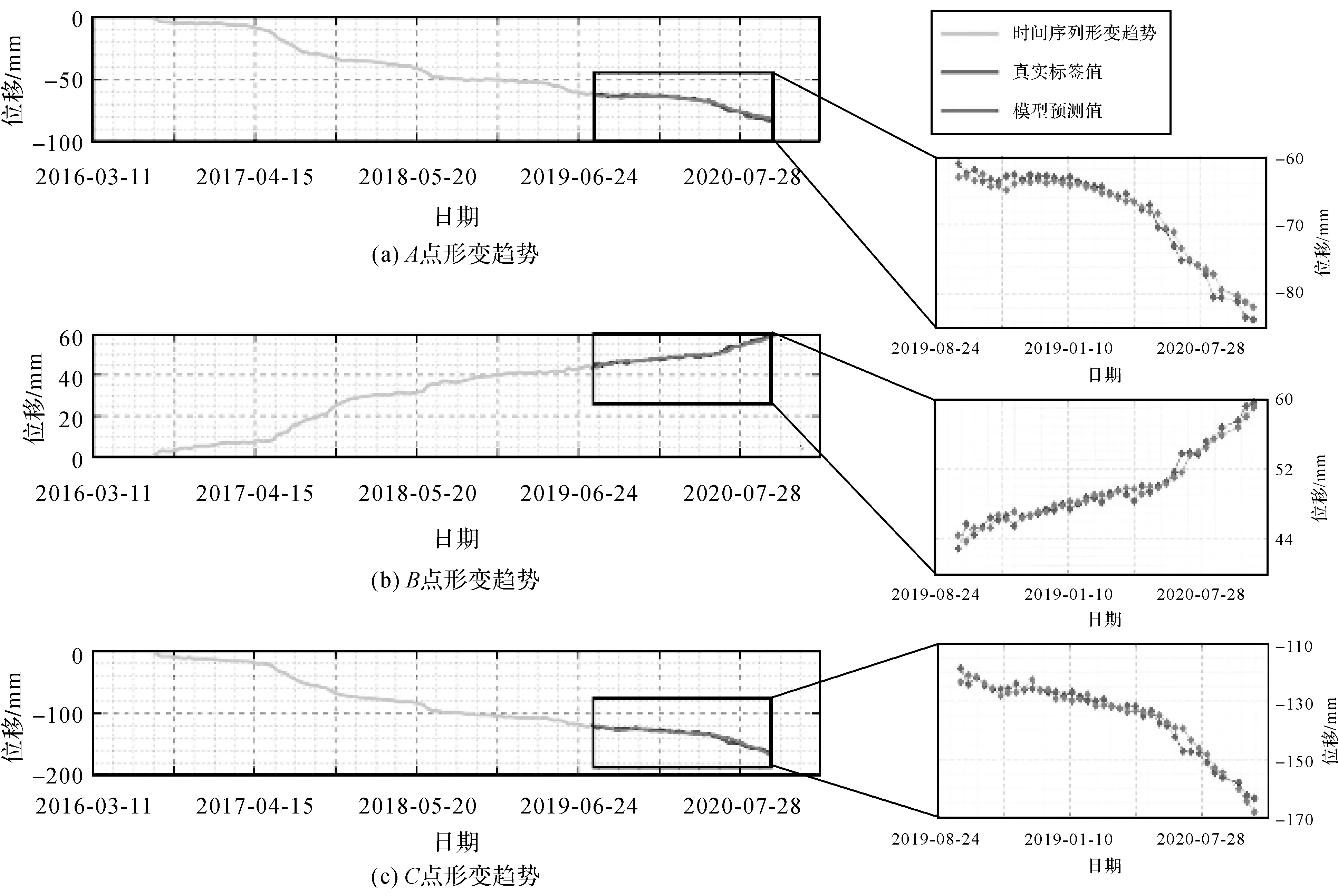
图7 A、B、C 3点形变趋势Fig.7 Deformation trend diagram at A,B and C points

选取均方根误差(RMSE)、平均绝对误差(MAE)及标准差(SD)3种时间序列评价指标对预测结果和真实标签的差异进行评估，计算结果见表5。可见，N-BEATS网络模型预测形变趋势结果的各项误差指标均满足形变预测的要求，进一步从真实数据试验的角度说明了该方法的可靠性。

表5 预测效果评价

现将时序预测得到的部分结果陈列如图8所示。图8列出了2019年8月22日、2019年12月8日、2020年3月25日及2020年6月17日的预测形变结果、真实观测的形变结果及二者之间的残差图。可以发现，在直观的目视判别中二者几乎相差无几，虽然在局部出现了残差高值，但在整体范围内仍然表现出的是较为均一且不超过±1 cm的预测偏差，说明预测效果较好。

图8 部分时间序列形变预测结果对比及其残差图Fig.8 Comparison and residual diagram of partial time series deformation prediction results

3.4 方法对比

图9为STL、支持向量回归(support vector regression,SVR)、无损卡尔曼滤波(unscented Kalman filter,UKF)、一次指数平滑法(single exponential smoothing,SES)及N-BEATS 5种时序预测方法在不同噪声水平数据下的应用效果对比，该节所选取的数据仍为3.1节中提到的P点时间序列数据。可见本文应用的N-BEATS网络模型在原始时序数据及添加毫米级和厘米级误差序列数据的应用效果都优于其他方法，达到毫米级的预测精度。在为原始时序数据添加毫米级噪声后，N-BEATS模型能够抵抗噪声干扰，完成高精度预测如图9(b)所示，然而对于添加厘米级噪声数据的抗差性能降低如图9(c)所示，可见该模型具有一定的抵抗数据噪声的能力，这一特点表明本文提出的方法对于输入形变序列的精度要求较低，即使序列中存在厘米级误差，仍能够获得相对更优的预测成果从而扩展N-BEATS神经网络预测的应用广度。

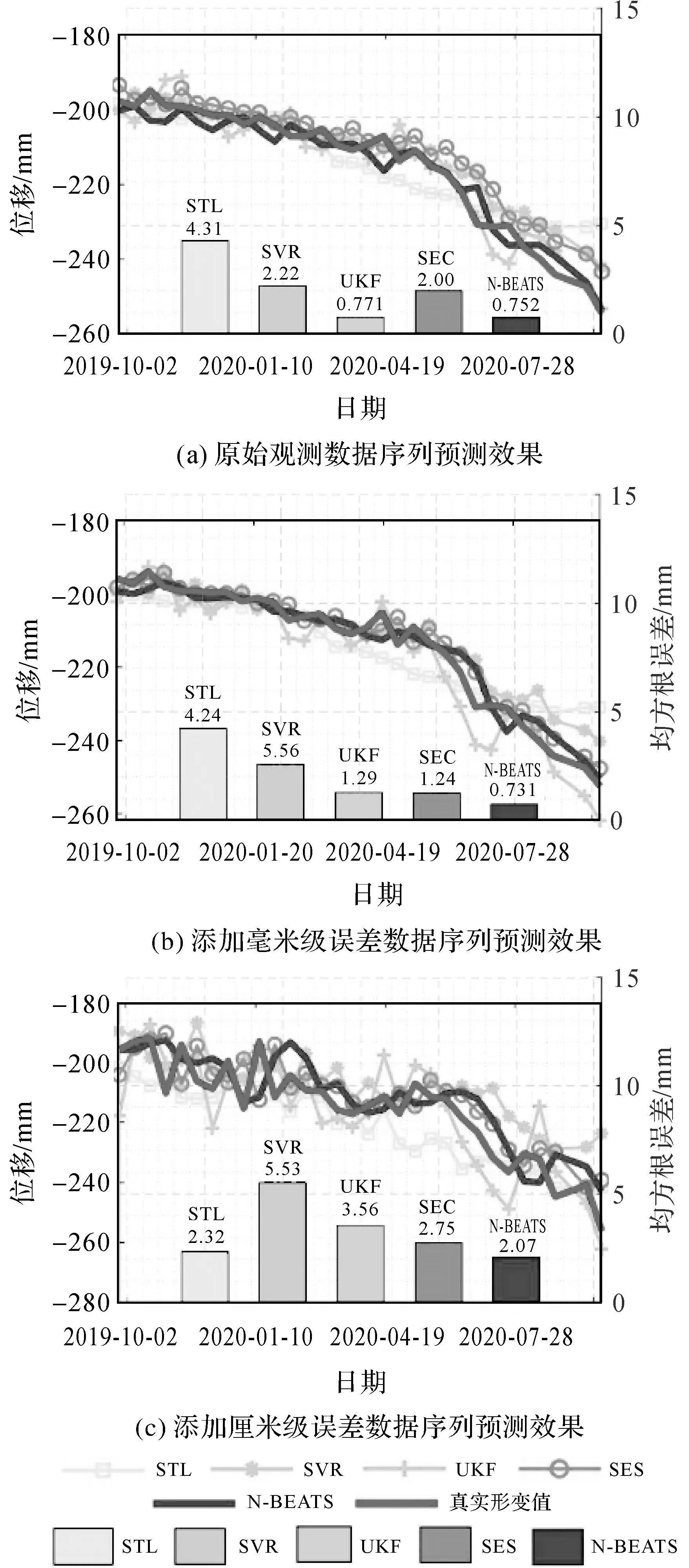
图9 N-BEATS与4种时序预测方法在不同噪声水平数据下的应用效果对比Fig.9 Comparison of N-BEATS and four time series prediction methods in different noise level data

3.5 预测区间估计

由于点估计存在误差，仅对滑坡形变做出点估计仍不充分，因此为衡量N-BEATS神经网络模型预测滑坡形变数据的可靠度和精度水平，本文对N-BEATS网络模型的预测结果进行了置信区间估计。假设N-BEATS网络模型对InSAR数据的滑坡形变预测结果服从正态分布X～N(μ,σ2)，给定可信度为95%，利用N-BEATS网络模型的300个对P点时序数据预测结果求取均值μ的置信区间估计如图10所示。对置信上限和置信下限分别计算均方根误差得到该模型预测的精度水平，可见对滑坡形变做300次预测的数据以95%的可靠性保证了预测误差在±10 mm之内。

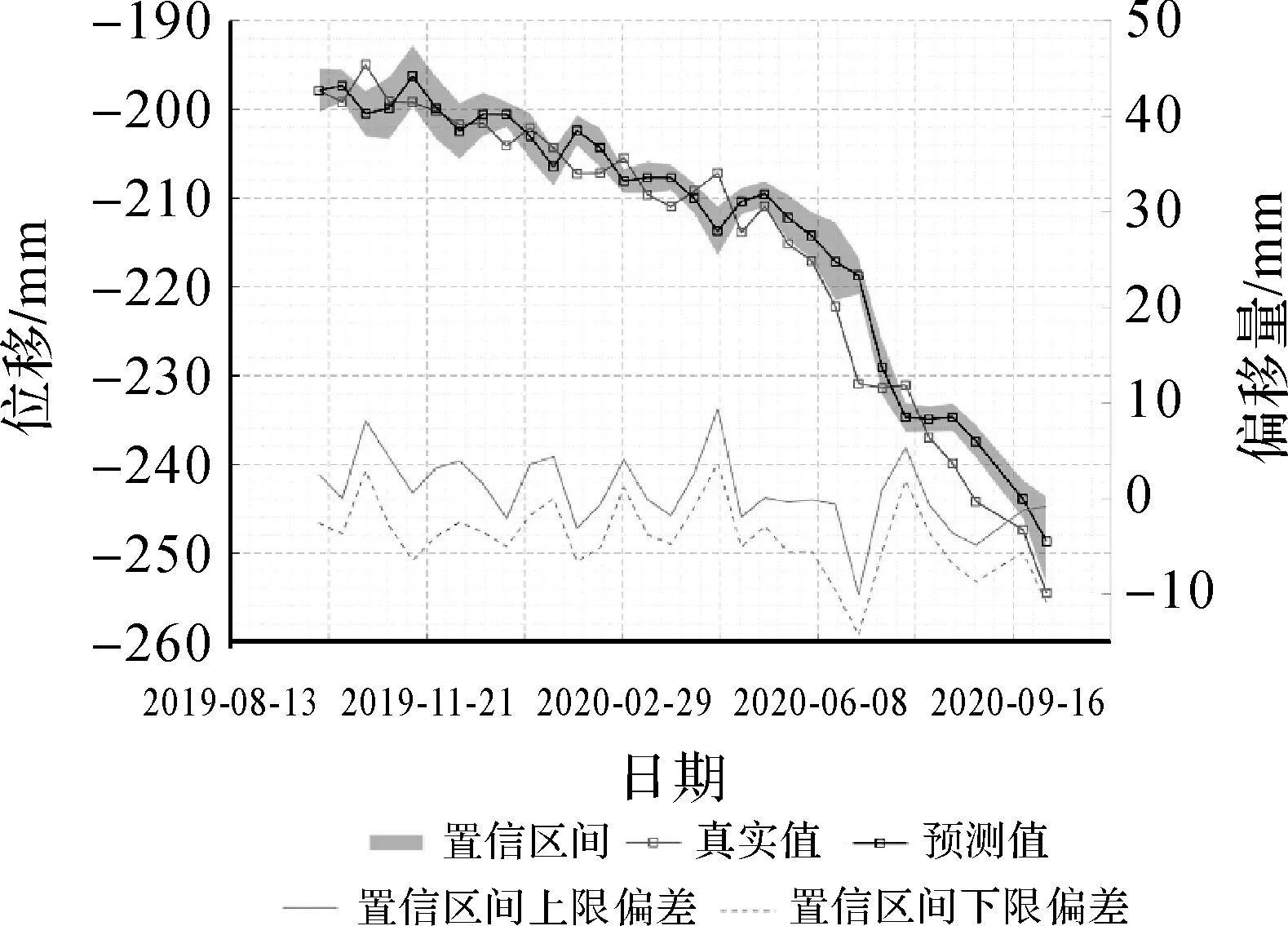
图10 N-BEATS神经网络置信区间估计Fig.10 N-BEATS Neural network confidence interval estimation

4 结论与展望

本文拓展了一种利用N-BEATS深度学习网络模型预测可解释性滑坡时间序列形变的方法，试验结果展示出该方法在滑坡预测应用中高可靠性、高精度及具有一定抗差能力的优势。三峡库区新铺滑坡真实试验结果表明以下4点。

(1) 针对本文所选取的时间间隔为12 d一景的Sentinel-1数据，选取单次预测输入输出窗口大小为[10,2]的数据结构能够在满足中短期滑坡预测的前提下取得较好的预测效果。

(2) 新铺滑坡应用N-BEATS网络模型进行预测，以均方根误差为1.1 mm的高预测精度完成了滑坡预测工作，证实了N-BEATS网络模型在时间序列预测任务上的有效性、可靠性及其工程实践性。

(3) 对原始滑坡形变时序数据添加毫米级和厘米级误差验证N-BEATS网络模型预测的抗差性能，与其余4种传统时间序列预测方法相比仍能够保持最高精度水平的预测，特别是针对存在毫米级误差的时间序列数据该方法体现出了良好的降低偏差预测功能。

(4) 利用N-BEATS网络模型对滑坡形变做300次预测，分析了该方法预测结果数据能够以95%的可靠性保证预测误差在±10 mm之内。

虽然利用N-BEATS网络模型进行新铺滑坡的形变预测取得了良好的效果，但在滑坡智能预测方面仍存在着许多有待解决的问题，例如预测时间跨度取决于训练数据的时间跨度而无法满足超越InSAR时间分辨率的短期预报需求；目前的时序预测模型仍停留在逐点预测的阶段，但不可否认的是逐点预测非常耗时且忽略了空间相关关系这一信息；单变量预测的突发性滑坡预测结果尚存在时间延迟问题等，在未来越来越多的SAR卫星(座)成功发射之后，有可能实现利用InSAR形变数据预测突发性形变的愿景。此外，InSAR数据与其他高时间分辨率数据融合也有助于实现形变序列数据的突发性预测。