基于深度学习的滑坡位移时空预测

罗袆沅，蒋亚楠,，许 强，廖 露，燕翱翔，刘陈伟

1. 成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059； 2. 成都理工大学地球科学学院,四川 成都 610059； 3. 四川测绘地理信息局测绘技术服务中心，四川 成都 610081

滑坡是陆地环境中普遍存在的一种地质灾害，对人类生命财产乃至整个社会经济系统构成严重威胁[1]。为减少人员伤亡和财产损失，当前，许多国家已建立了针对典型重大滑坡的监测预警系统[2]。而监测系统获取的时序位移数据集通常能够直接反映滑坡的变形或稳定特征[3]。因此，监测数据集对于构建高效的预测预报模型，实现滑坡灾害动态预测预警具有重要应用价值。

滑坡位移预测模型除了复杂的物理模型，还包括基于监测数据集的数理模型[4]。与物理模型相比，数理模型的建立过程更简单、精确[5]。然而，滑坡变形演化是一个非线性动力作用过程，受地形地貌、岩土结构、水文地质、气候和人类活动等因素的影响[6]，存在时空相关性。因此，数理模型中的机器学习方法因能处理非线性时序的复杂性、动态性和非线性特征，被广泛应用于滑坡位移时序预测。近年来，人工神经网络(artificial neural network,ANN)[7]、支持向量机(support vector machine,SVM)[8]、极限学习机(extreme learning machine,ELM)[9]和循环神经网络(recurrent neural network,RNN)[10-11]等机器学习方法广泛应用于滑坡位移预测。但是，这些预测模型只考虑了位移监测数据的时间相关性，可实现单个典型监测点的位移预测，忽略了监测点之间的空间相关性。一定程度上限制了预测精度的提高，且无法准确地判断滑坡整体变形趋势，从而导致潜在的威胁被忽视。

图神经网络(graph neural network,GNN)因能把实际问题看作图或网络节点之间的连接和消息传播问题，并捕获图结构数据中节点间的空间关系，而被广泛应用于交通、海表温度等领域的时空预测[12-14]。而卷积神经网络(convolutional neural network,CNN)的引入，使得非欧氏数据也能得到有效的处理[15]。因此，通过图卷积网络(graph convolutional network,GCN)[16]捕获滑坡GNSS监测网中各监测点间的空间相关性，理论上是可行的。同时，门控循环单元(gate recurrent unit,GRU)[17]是一种缓解梯度爆炸与弥散问题的循环神经网络，它能有效地捕获时序数据的时间相关性，并在训练时间、参数更新和泛化能力方面优于其他循环神经网络，已在经济学、防洪减灾、能源等应用[18]中显现出明显的优势。

基于以上认识，本文提出一种基于深度学习的滑坡位移时空预测模型。该模型将滑坡GNSS监测网看作非欧氏图结构数据，并考虑到监测点间的时空相关性，采用GCN与GRU结合的时态图卷积网络(temporal graph convolutional network,T-GCN)模型[19]，从而实现滑坡位移的时空预测。通过白水河滑坡位移监测数据进行建模验证，并结合消融试验验证了外界影响因素属性的增强能进一步提高模型的预测性能。试验结果证明，与主流的时序预测方法相比，该方法预测效果具有明显优势，可用于滑坡位移或其他地质灾害中同样具有时空关联属性的观测量的时空预测。

1 基于深度学习的滑坡位移时空预测模型

由于滑坡位移变化具有时空相关性，应将其作为时空预测任务。本文提出了一种基于深度学习的滑坡位移时空预测模型，该模型由可捕获监测点间空间相关性的图卷积网络GCN，及获取监测点上位移数据时间相关性的门控循环单元GRU两个模块组成。流程如图1所示：首先，滑坡位移监测数据通过预处理得到时间相关和空间相关的数据；其次，将外界影响因素作为滑坡监测点属性信息，结合滑坡位移时序特征建模获得增广特征向量，即为属性增强的时间相关数据；最后，利用预处理后的时空图结构数据，采用T-GCN模型实现滑坡位移的预测。

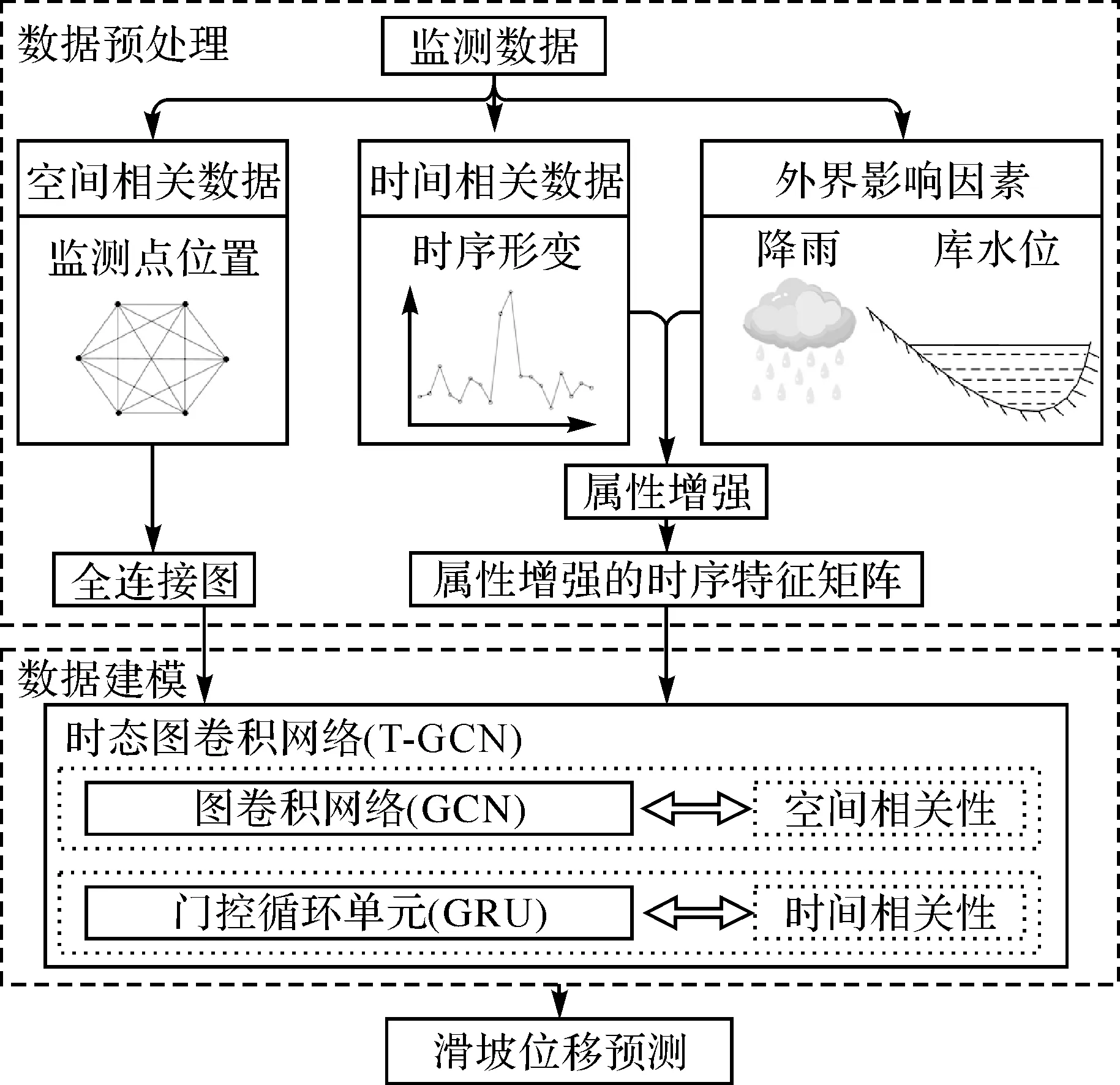
图1 预测方法流程Fig.1 Forecast method flowchart

1.1 构建图结构数据

1.1.1 时空相关的属性表达

如图2所示，为表征监测点之间的空间相关性，定义一个加权无向全连接图G=(V,E,W)。其中，V={v1,v2,…,vN}为图的节点(GNSS位移监测点)，N为监测点个数，每对监测点具有一条连接边，连接边E的总数为N×(N-1)/2。W∈RN×N表示监测点间相关性的邻接矩阵。

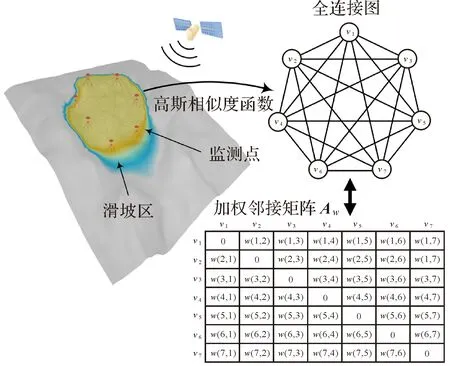
图2 加权全连接Fig.2 Weighted full connection

(1)

式中，较大的权值说明两监测点具有较高的空间相关性。

构建包括所有监测点的时序形变信息的特征矩阵X∈RN×P来表征滑坡位移的时间相关性，P为时序长度。X∈RN×t为所有监测点t时刻的相对位移。若n个历史时序数据的输入为[Xt-n,…,Xt-1,Xt]，则未来T个时刻的预测值为[Xt+1,…,Xt+T]。

1.1.2 考虑外界影响因素的属性扩展

滑坡的变形破坏离不开自身地质结构、地形地貌等内在条件的驱动，以及外在人类活动、气候、径流等条件的加持，原本稳定的滑坡也会突发强烈变形。而影响库岸滑坡稳定性的外在因素主要是降雨和库水位变化[21]。通常，库岸滑坡复活后，库水位的周期调度及降雨的联合作用容易引起斜坡内地下水位的波动，加速滑坡的变形失稳[22]。文献[23]将影响交通条件的外部因素视为交通流量预测的属性增强，并作为属性矩阵与特征矩阵推导出增广矩阵，提高了模型预测精度。同理，本文采用降雨和库水位作为属性增强，以获取滑坡位移增广矩阵，进一步提高滑坡位移预测精度。

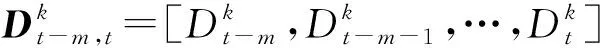
(2)

式中，k为2，即表示降雨和库水位两个属性，St∈RN×(P+k*(m+1))。

综上所述，滑坡位移预测问题可被看作是基于全连接图和特征矩阵来学习映射函数f(式3)，从而获取未来时段T的滑坡位移信息

f(G,X|D)=[Xt+1,Xt+2,…,Xt+T]

(3)

1.2 预测方法原理

1.2.1 图卷积神经网络

在滑坡位移时空预测中，实现监测网中监测点间的空间相关性表达至关重要。GNSS监测网为典型的非欧氏图结构，GCN可有效捕获非欧几里得结构中的空间相关性，在考虑到相邻节点影响的同时，能够获取图结构中每个节点的特征[25]。如图3(a)所示，为捕获拓扑结构的依赖性，GCN以邻接矩阵A和特征矩阵X为输入，其传播过程为

(4)

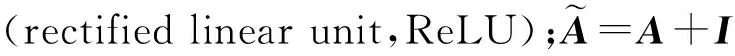
图3 两种深度学习模型的结构Fig.3 Architectures of two deep learning models

1.2.2 门控循环单元

GRU是循环神经网络的一种变体，常用于分析时序数据，其优势在于可以自适应地捕捉不同时间尺度的依赖关系。GRU通过门控单元来调节单元内部的信息流，不单独设置存储单元，结构更加简单，并在训练时间和更新优化上相比长短期记忆模型(long short-term memory,LSTM)更高效[17,26]。

如图3(b)所示，GRU由重置门和更新门组成，若当前时间特征矩阵为xt，ht-1表示上一时刻t-1的隐藏状态。重置门rt用于决定输入状态与历史信息的结合程度，即候选隐藏状态ct，更新门ut用于控制历史信息的忽略程度，并结合候选隐藏状态ct推导出最终隐藏状态ht。其中，σ和tanh为激活函数。

1.2.3 时态图卷积网络

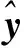
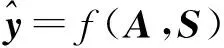
(5)

若当前时刻为t，St为此时刻所提取的属性增强矩阵，将其输入多层GCN以生成具有滑坡空间相关的时序变化特征。然后，使用这些特征序列作为GRU的输入，以构建时间依赖关系，并推导出隐藏滑坡位移状态。推导过程为

ut=σ(Wu·[gc(St,A),ht-1]+bu)

(6)

rt=σ(Wr·[gc(St,A),ht-1]+br)

(7)

ct=tanh(Wc·[gc(St,A),(rt*ht-1)]+bc)

(8)

ht=ut*ht-1+(1-ut)*ct

(9)

式中，gc(·)表示图卷积过程；σ(·)和tanh(·)为激活函数；参数W和b分别为权值和偏差；[·]表示向量相连；*为矩阵的卷积。

综上所述，时空预测模型的整体框架图4所示，主要分为数据预处理、加强属性特征、T-GCN建模和预测4个部分。

图4 预测模型框架Fig.4 Prediction model framework

1.3 模型评价指标

本文基于3个指标来评估模型的性能：①平均绝对误差(mean absolute error,MAE)；②平均绝对比例误差(mean absolute scaled error,MASE)；③均方根误差(root mean square error,RMSE)。

MAE为绝对误差的平均值，其值越小意味着预测模型的性能越好

(10)

MASE是对时间序列预测准确性的一种度量[27]。对于时间序列数据，通常使用最近观测值的方法定义一个比例偏差值

(11)

同理，RMSE值越小，预测误差越小，模型的性能也越好

(12)

2 白水河滑坡试验与结果分析

2.1 试验区与试验数据

白水河滑坡隶属湖北省宜昌市秭归县，距三峡大坝56 km，为三峡库区中典型的松散堆积层滑坡。滑坡总体坡度约为30°，平均厚度约为30 m，体积约为1260×104 m3；滑面为残坡积层与基岩接触带，厚约0.9～3.1 m，基岩岩性为中厚层砂岩夹薄层泥岩，产状15°∠36°，岩层中节理裂隙发育；滑体物质主要由第四系残坡积碎石土组成，碎石含量20%～40%[28]。根据白水河滑坡的变形特征、观测通视情况，确定监测内容以地表位移监测为主。白水河滑坡点监测点分布如图5所示，监测初期在3个纵向剖面上共布置7个GNSS监测点(ZG91、ZG92、ZG93、ZG94、ZG118、ZG119和ZG120)。2005年5月之后，在预警区内增设了4个GNSS监测点(XD-01、XD-02、XD-03和XD-04)。顾及监测数据的长时序特征，本文仅采用初期布设的7个GNSS监测点的位移监测数据，构建高斯相似度函数表征空间相关性。所用时序数据范围为2003年7月—2013年3月，滑坡GNSS月相对位移监测数据，三峡库区的同步库水位及当地降雨量数据(图6)。

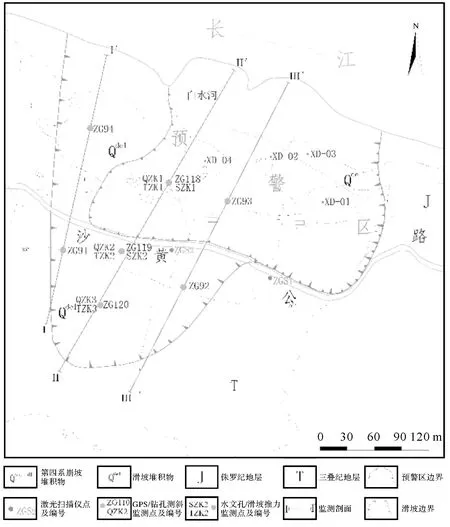
图5 白水河滑坡监测点分布Fig.5 Baishuihe landslide monitoring points distribution

数据的空间相关性，通过高斯相似度函数连接7个监测点，并构建7×7的加权邻接矩阵Aw。矩阵中的值表示两监测点之间的相似性。对于时间相关数据，通过GNSS监测的时序形变数据构建7×117的特征矩阵X。每一行表示一个监测点，对应列为该点的时序形变值。对于外界影响因素数据，结合特征矩阵、降雨量和库水位数据构建7×117×3的属性增强矩阵S。此外，采用x=(x-min)/(max-min)将数据归一化到[0,1]之间，并将2003年7月—2011年8月的数据用于模型训练，2011年9月—2013年3月的数据用于模型测试。

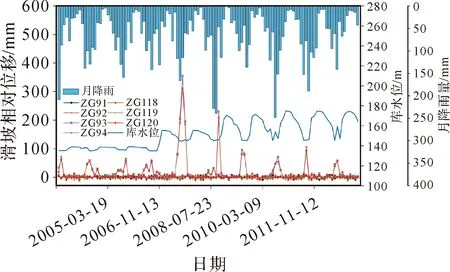
图6 滑坡相对位移-降雨量-库水位关系Fig.6 Relationship between landslide relative displacement rainfall reservoir water level

2.2 空间相关性和影响因素分析

2.2.1 空间相关性

引入灰色关联度评估监测点之间的空间关联性，若灰色关联度>0.6，可认为两者密切相关[24]。以预警区内相邻的两点ZG93和ZG118为例，其灰色相关度计算结果为0.74，如图7所示，两者位移变化趋势基本一致，表明两者之间具有很强的空间相关性。而由图6和表1可知，预警区外的监测点位移变化趋势较小，大都在20 mm内上下波动，且变化趋势也基本一致。同时，预警区外监测点之间灰色关联度均在0.6以上，且距离越近，灰色关联度越大。因此，预警区外的监测点之间同样具有强空间相关性。结合图8分析，由于受距离的影响，ZG92和ZG93在局部变化趋势上具有相似性，且灰色关联度为0.54，故预警区内外的监测点同样具有相关性。综上所述，整个监测网中监测点间具有不同强度的空间相关性，并证实了滑坡位移预测需要考虑到监测点间的空间关系，这是不可忽略的重要因素。

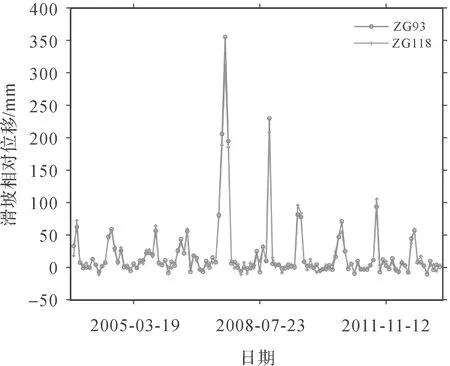
图7 预警区内监测点相对位移Fig.7 Relative displacement of monitoring points in early warning area

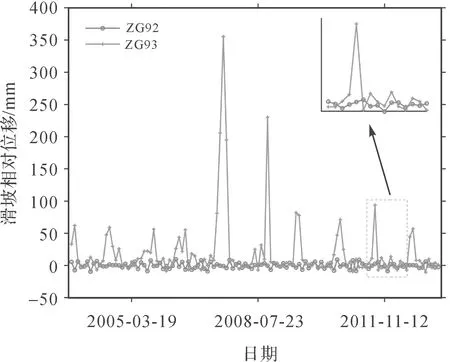
图8 预警区内外监测点相对位移Fig.8 Relative displacement of monitoring points inside and outside the early warning area

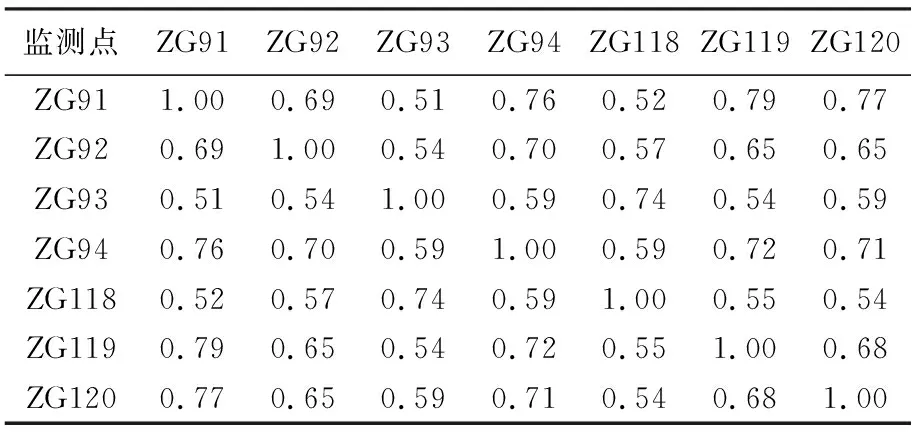
表1 灰色关联度分析

2.2.2 影响因素

作为三峡库区内典型的库岸滑坡，影响白水河滑坡稳定性的主要外在因素为降雨和库水位。如图9所示，强降雨的出现和库水位的快速下降往往伴随着滑坡位移的突变。然而，滑坡位移的突变总是滞后于两者变化。其中，降雨入渗促使坡体基质吸力趋于零、斜坡容重增加，导致坡体抗剪强度下降、下滑力增大[21]，从而影响滑坡稳定性。而库水位的变动改变了坡体内的渗流场分布和岩土体的应力状态。且库水下降越快，在坡体内外形成的水力梯度越大，沿坡体向外的渗流力极大地影响了滑坡体的稳定性。综上分析可得，滑坡位移的变化受降雨和库水位的影响，且具有强相关性。

图9 滑坡相对位移与影响因素关系Fig.9 Relationship between relative displacement of landslide and influencing factors

2.3 模型训练及参数设定

样本划分方式如图10所示，训练样本从左至右滑动抽取。在本文试验中，每次抽取6个样本，前5个作为样本输入，第6个作为标签，测试集采用同样方式处理。为提高训练速度，采用批方式传递数据给模型，通常批大小为32[13]。试验中采用ReLU作为图卷积的激活函数，适应性动量估计(adaptive moment estimation,ADAM)[29]算法作为优化器，训练过程中的损失函数定义为

(13)

学习率为控制输出误差反向传播至网络的权值参数，默认初始值为0.001，并通过ADAM优化器进行自适应动态调整。然而，隐藏神经元(门控循环单元)个数，以及模型的训练次数是影响预测精度的关键，本文通过多组试验确定。

首先，设定隐藏神经元个数设置为64，分析训练次数对模型性能的影响，设置训练次数为[100,250,500,1000,1500,2000]并进行了测试。如图11所示，随着训练次数的增加，评价指标趋于稳定，转折点为1000次，同时模型预测性能达到最优。然后，设定训练次数为1000次，测试隐藏神经元个数对模型性能的影响，从[8,16,32,64,100,128]中选择最优的隐藏神经元个数。如图12所示，随着神经元个数的增加，模型变得稳定，且在个数为64时最优。因此，本文试验的训练次数设定为1000次，隐藏神经元个数设定为64个。

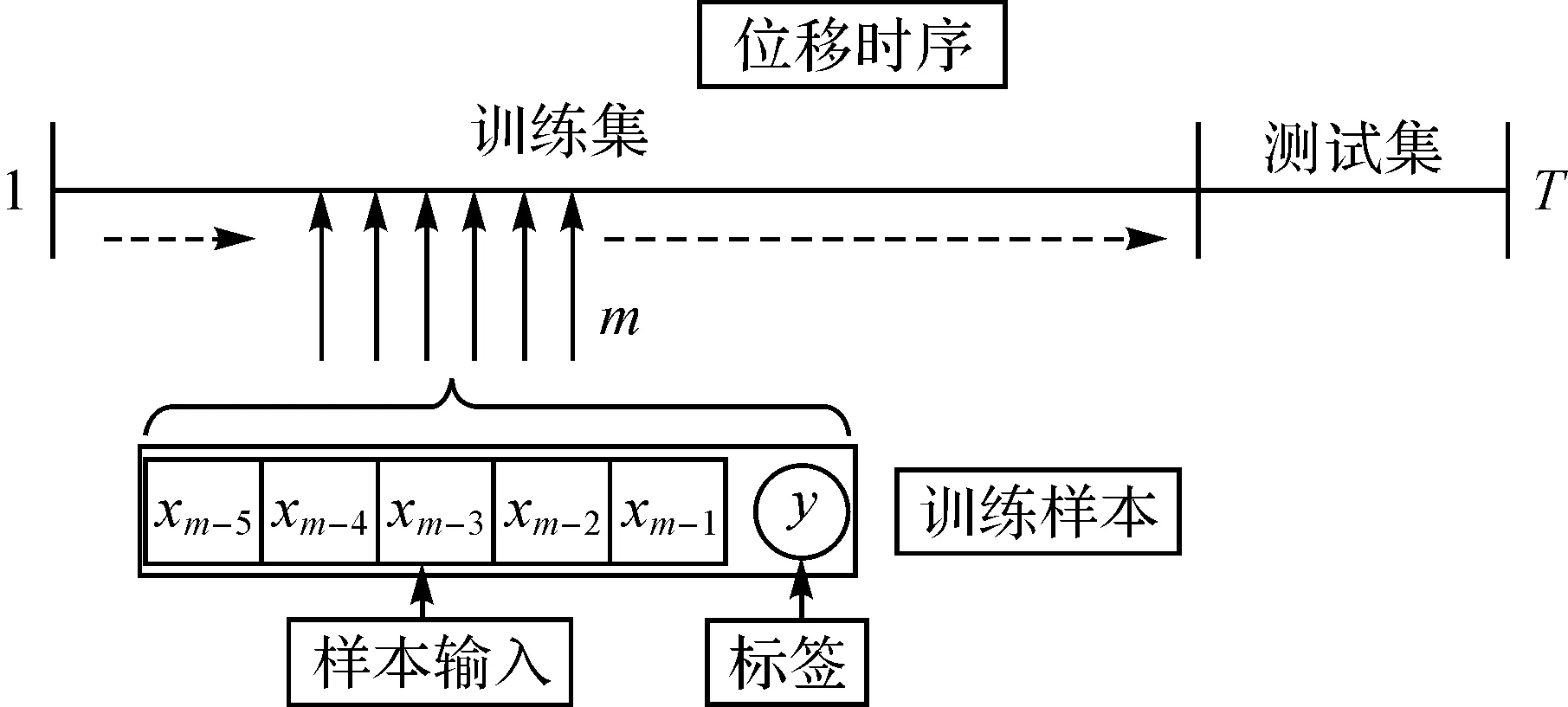
图10 样本划分Fig.10 Sample division

图11 不同训练次数的选择对预测性能的影响Fig.11 The influence of the selection of epochs on the prediction performance

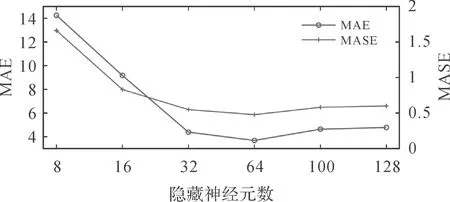
图12 不同隐藏神经元个数的选择对预测性能的影响Fig.12 The influence of the selection of units on the prediction performance

2.4 预测结果分析

试验设计时考虑了以下两个方面：与其他时间序列预测模型的精度比较，以及引入不同类型外界影响因素时对模型性能的影响。计算机配置：Intel Core i5-9400F CPU和32G RAM的台式电脑；程序语言：TensorFlow2.1、Python3.6、Matlab2020a。

2.4.1 对比分析

为验证本文方法相较于时间序列预测方法的优势，采用自回归移动模型(auto regressive integrated moving average,ARIMA)[30]、多元线性回归(multiple linear regression,MLR)[31]等传统时间序列预测方法，以及支持向量回归机(support vector regression,SVR)[8]、长短期记忆模型LSTM[32-33]等主流机器学习方法进行对比分析，结合建模时间与评价指标判断模型性能优势。不同于本文的预测模型，上述方法只能对单个滑坡监测点进行建模预测。因此，使用GNSS监测的时序形变数据构建的7×117的特征矩阵X，分7次建模预测，得到最终7个监测点的位移预测值。此外，增加了无属性增强的时态图卷积网络T-GCN的深度学习方法进行对比分析，以验证属性增强可提高模型预测的性能。

白水河滑坡的7个监测点结果，如图13所示，每个监测点的预测值与实际值变化趋势一致，非预警区内监测点的误差均控制在10 mm之内，而预警区内监测点主要在突变处出现较大的误差，最大误差为16.66 mm。

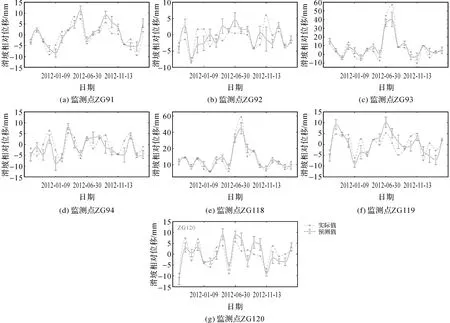
注：紫色竖线为绝对误差值。图13 滑坡位移整体预测对比Fig.13 Comparison diagram of overall prediction of landslide displacement

结合表2，本文模型整体预测的3个预测指标大小为：MAE在4 mm以内，MASE为0.477，RMSE为4.429 mm，均为最优表现。为更好地展现预测结果的局部细节，以监测点ZG93(图14、图15)为例，本文模型与实际值具有很高的吻合度，特别是在转折点和峰值处都优于其他方法。结合整体预测评价指标的优势，对比分析如下。

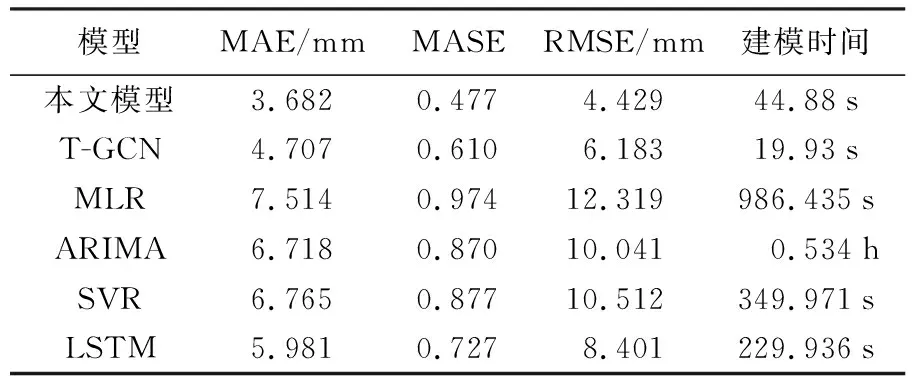
表2 不同预测模型的试验结果对比

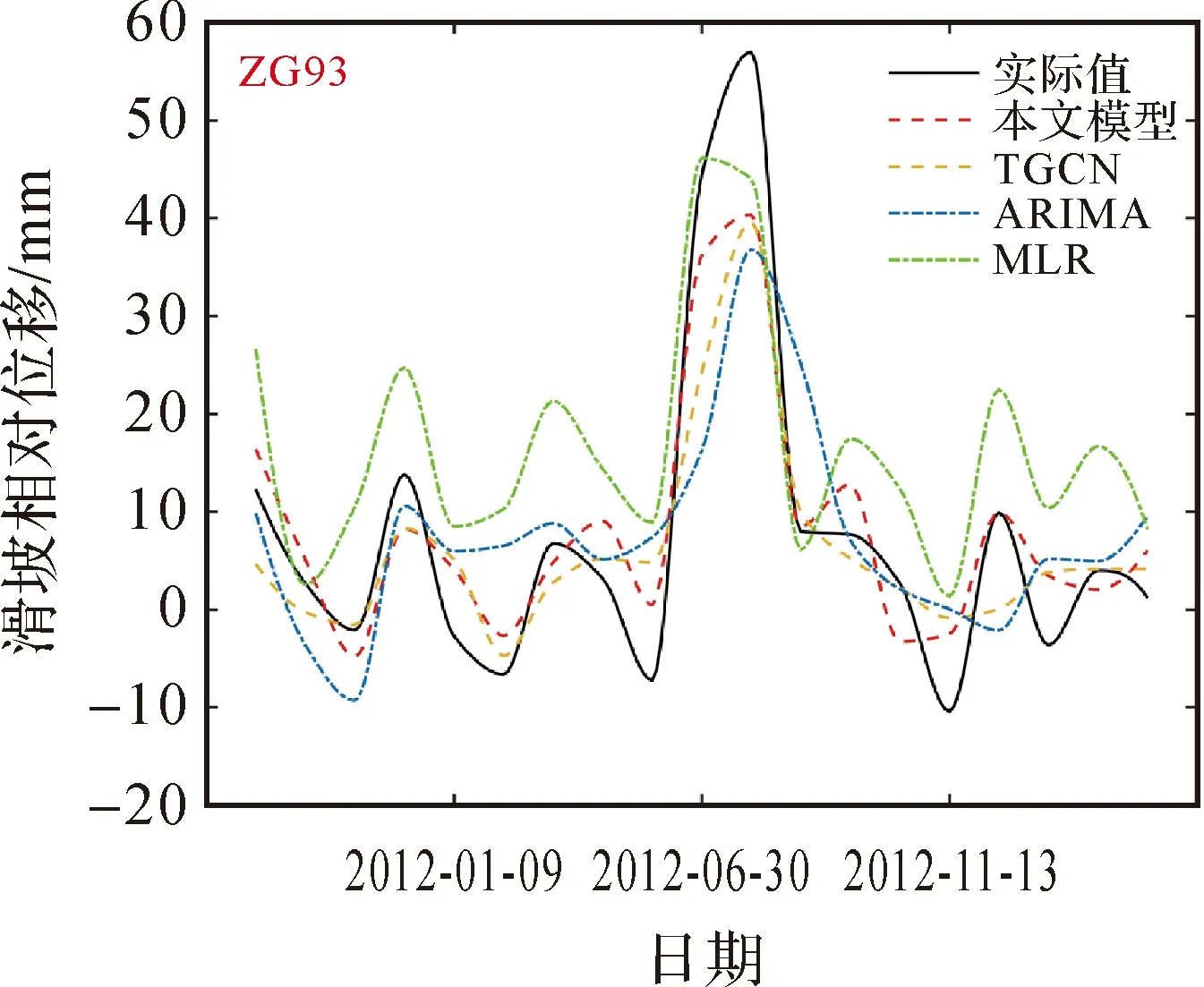
图14 传统预测方法对比结果 Fig.14 Comparison results of traditional prediction methods

图15 机器学习方法对比结果Fig.15 Comparison results of machine learning methods

(1) 与基于数理统计的传统预测模型(MLR、ARIMA)相比，本文模型RMSE明显低于两者，分别减少了约64%和55.9%。传统预测方法与实际值波动趋势基本一致，但相对误差较大。说明传统预测方法可以捕捉滑坡位移的时序变化趋势，但无法顾及变化的量值大小。

(2) 与传统的机器学习SVR模型相比，本文模型RMSE降低了约57.9%。而相对于只关注时间相关性的LSTM模型，本文模型因顾及到时空相关性在各项指标上均有更好的表现，RMSE减少了约47.3%。SVR在转折点处的预测误差相对减小，而LSTM在整体上表现较好。但是本文模型无论是在整体趋势上，还是在转折点和峰值处，都具有最好的表现。

(3) 从引入外界影响因素的角度来看，相比未属性增强的T-GCN模型，本文模型RMSE降低了约28.4%，各项指标均更优，并更能顾及转折点处量值大小。

(4) 由于MLR、ARIMA、SVR和LSTM均需对单个监测点进行独立建模预测，因此这些预测模型在建模时间上均远远超过本文方法。其中，ARIMA需要对每个监测点求取最优参数，所需时间成本大大增加。而T-GCN由于未考虑属性增强模型，处理数据量小，因此在建模时间上小于本文模型。

综上所述，基于深度学习的滑坡位移时空预测模型精度较高，时间成本较低，是一种更满足生产需求的高效预测方法。

2.4.2 消融试验分析

为证实滑坡主要的外界影响因素(降雨和库水位)具有提高属性增强模型预测性能的能力，在上述基础设置的前提下进行消融试验：分别为只添加降雨属性增强、只添加库水位属性增强以及两者均添加的属性增强。由整体预测结果评价指标(表3)可知，无论是添加降雨属性增强还是库水位属性增强，两者均相较于未属性增强的T-GCN模型在各项指标上显著提升。而同时添加降雨和库水位属性增强时，本文模型各项指标表现最好。从细节角度来看(图16)，库水位因素的添加提高了模型对峰值和转折点的感知能力，其预测结果在峰值和转折点比降雨属性增强更接近实际值。而降雨因素的添加提高了模型对变化趋势的预测能力，其预测结果比库水位属性增强在趋势上更接近实际情况。然而，同时兼具库水位和降雨属性的预测结果与真实值之间的误差更小，趋势更接近。

表3 不同设置的消融试验

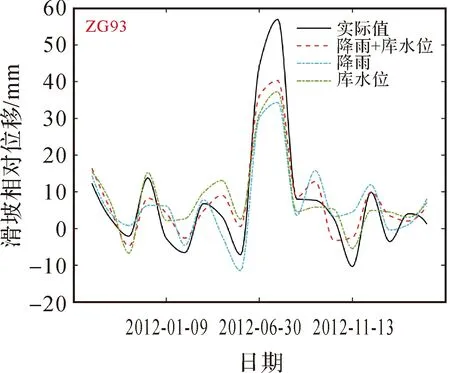
图16 消融试验结果Fig.16 Results of ablation experiments

由以上分析结果可知，无论单独添加降雨因素或者库水位因素，两者的位移预测能力基本相当，说明降雨和库水位对滑坡位移的影响几乎一致，均方根误差分别降低了0.29%和0.11%。同时添加两种因素比添加单一类型因素的模型表现更好，从而也证实了降雨和库水位联合作用于滑坡变形[19-20]。因此，采用外界影响因素有助于增强滑坡位移预测模型能力。

3 结 论

本文通过考虑滑坡位移监测系统中所有监测点之间的空间和时间相关性，并综合了外界因素对滑坡位移的影响，提出了一种基于深度学习的滑坡位移时空预测模型。试验结果表明。

(1) 相比传统的回归预测方法和经典的机器学习方法，本文所提时空预测方法结果的均方根误差为4.429 mm，至少降低了47.3%，并在预测精度与时效方面更具优势。

(2) 与针对单个监测点的滑坡位移预测模型相比，基于全局的滑坡位移预测方法兼顾了时间和空间上的相关性，在缩短了预测时间的基础上提高了整体预测精度，进而更好地揭示整个监测系统的位移变化情况，为滑坡预警预报提供更准确的数据支持。

(3) 考虑到外界影响因素对滑坡变形趋势的影响，相比直接采用位移特征属性的预测方法，时空预测方法通过属性增强提高了模型的预测性能，均方根误差减少了28.4%。

但是滑坡区域内的监测点受剖面和所在滑坡体位置的限制，所有监测点之间不只有空间度量关系，可能含有空间拓扑关系，需要更进一步试验和论证。除此之外，本文采用降雨和库水位两个因素，未考虑到两者的周期性的此消彼长变化特征对滑坡变形的影响，如何提取有效的周期特征，以实现更具解释力的滑坡预测结果也将是后续的研究重点。