基于三角剖分和轮廓分析的船舶焊缝特征识别
2022-11-04戴现令申燚曹荣祥孙宏伟袁明新
戴现令, 申燚*, 曹荣祥, 孙宏伟, 袁明新
(1.江苏科技大学机械工程学院, 镇江 212003; 2.江苏自动化研究所, 连云港 222006)
焊接是船体制造中的重要环节,由于焊接烟尘、弧光和金属飞溅等的存在,焊接工作环境往往比较恶劣[1]。利用焊接机器人开展自动化焊接,不仅能提升焊接质量的一致性,而且可以提高生产效率、降低成本。但焊接工艺参数的快速、准确选择是关键,而这需要先对焊接件数字模型中焊缝特征进行精确识别。焊缝特征识别一直是自动化焊接领域的研究重点,目前研究主要集中在对焊缝图像或数字点云模型的处理。Xiao等[2]针对由激光视觉传感器获得焊缝的3D点云数据,在利用边缘提取和Steger算法获得激光条纹特征点基础上,完成了平接和角接接头的V型坡口识别。Jawad等[3]基于主动视觉并结合颜色处理、中值滤波和像素邻域搜索,利用改进Otus算法提取出焊缝中心线上特征点,实现V型坡口的识别。张纶昭[4]基于Hessian矩阵提取图像中激光条纹中心点和方向信息,使用随机采样一致性算法拟合得到接头横截面的直线并通过相交点确定出焊缝中心点,实现T型角接和V型平接的坡口识别。张泽南等[5]通过SolidWorks API接口进行焊接件焊缝标注模块的二次开发,利用遍历特征树技术访问到切割清单,从而识别出平接接头和T型接头,并获取到焊缝厚度和宽度等信息。从上述研究可以看出,目前焊缝特征识别主要针对单一类型的焊缝,或是针对部分接头或个别坡口的提取,限制了其应用范围。为此,提出了基于三角剖分和轮廓分析的焊缝特征识别,首先通过基于有向三角形旋向的Delaunay三角剖分来生成三维模型的STL文件,然后基于STL文件进行焊缝特征识别。
1 Delaunay三角网格剖分
为了便于三角网格剖分算法的描述,首先给出如下基本定义。
1.1 基本定义
定义1如图1所示,设多边形存在n个顶点(n≥ 3),将全部顶点以逆时针方向编号,并记为P=[P1,P2,…,Pn]。定义多边形P1P2…Pn为域V,且存在若干三角剖分并组成集合W。∀Pi,Pj,Pk∈P,wijk=ΔPiPjPk∈W,W当且仅当满足以下条件[6]:①W中每个三角形除顶点之外,不含有其他顶点;②W中任意两三角形两者不交叠,且至多存在一个公共顶点或一条公共边;③W中任意一点都包含在域V中。
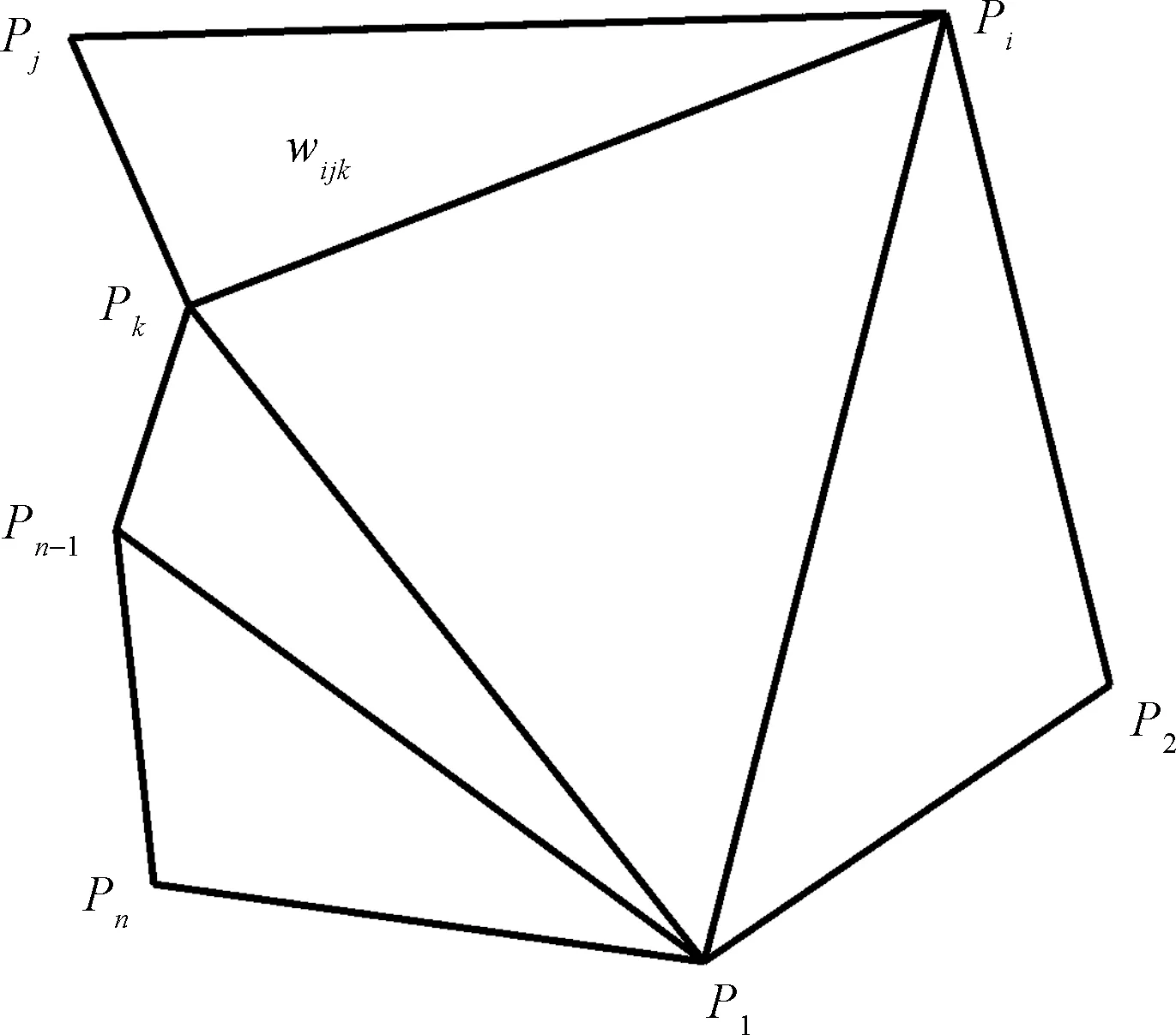
图1 三角剖分定义Fig.1 Definition of triangulation
定义2∀i∈[1,n-2],设Pi、Pi+1、Pi+2为域V中按逆时针连续排列的3个顶点,则定义Pi为Pi+1的前点,Pi+2为Pi+1的后点,前点Pi与Pi+1组成的边为前边,后点Pi+2与Pi+1组成的边为后边。
1.2 算法描述
Delaunay三角剖分主要是基于角系数法和有向三角形旋向实现,包括初始三角网格生成、三角网格局部变换和STL文件生成。
1.2.1 初始三角网格生成
步骤1顺序读入多边形域V的顶点P1,P2,…,Pn,并依次存储到数组空间。
步骤2通过角系数法判断每个顶点的凹凸性,获取所有凹顶点。
如图2所示,在待定顶点Pi+1的上、下设置两条距其距离相等的水平直线l1、l2,直线l1或l2分别与前边PiPi+1、后边Pi+1Pi+2的交点为A、B。设直线APi+1、BPi+1的斜率分别为tanα、tanβ,根据式(1)计算角系数差值Δ。若:交点A、B都在同一条水平直线上且Δ>0,则顶点Pi+1为凹顶点;反之,Δ<0,则顶点Pi+1为凸顶点。交点A、B不在同一条水平直线上且Δ>0,则顶点Pi+1为凸顶点;反之,Δ<0,则顶点Pi+1为凹顶点。
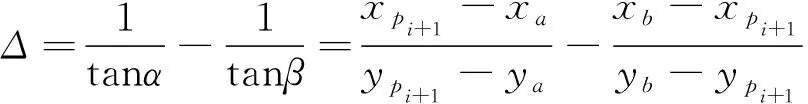
(1)
式(1)中:xa、ya为交点A横纵坐标值;xb、yb为交点B横纵坐标值;xPi+1、yPi+1为顶点Pi+1横纵坐标值。
此外,若前边PiPi+1或后边Pi+1Pi+2为水平直线时,则式(1)中1/tanα=0或1/tanβ=0。
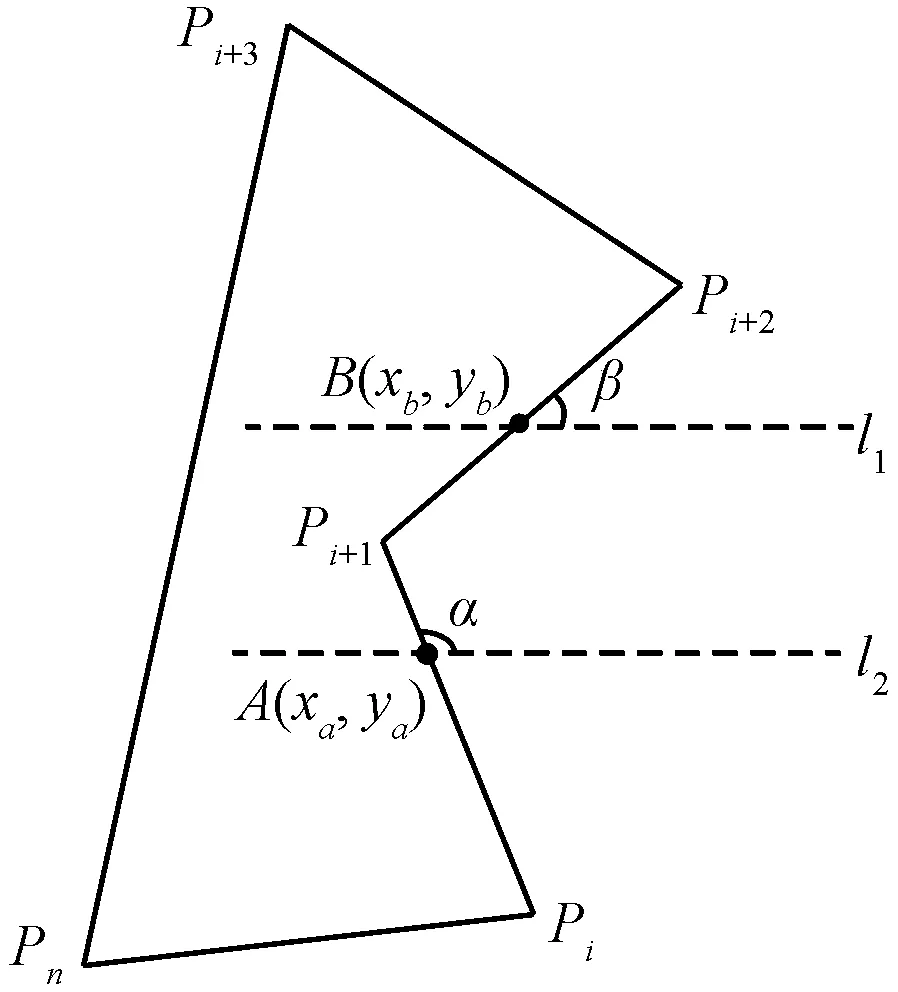
图2 凹凸顶点判断Fig.2 Concave and convex vertex judgment
步骤3∀j∈[1,n-2],按顺序从P中依次取出3个顶点Pj、Pj+1、Pj+2来构成有向三角形△PjPj+1Pj+2,并根据式(2)求出其面积S△PjPj+1Pj+2进行三角形旋向判断。如图3所示,若计算结果为正,则该三角形为逆时针旋向并转步骤4;反之为顺时针旋向并转步骤5。若3个顶点位于同一直线上,则也转步骤5。
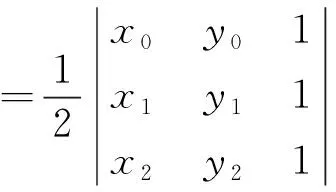
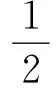
(x1-x2)(y2-y0)]
(2)
式(2)中:(x0,y0)为顶点Pj坐标;(x1,y1)为顶点Pj+1坐标;(x2,y3)为顶点Pj+2坐标。
以图2为例,三顶点Pi、Pi+1、Pi+2所构成三角形的旋向为顺时针;三顶点Pi+1、Pi+2、Pi+3所构成的三角形旋向则为逆时针。
步骤4判断三角形内部是否含有凹顶点。若无凹顶点,则输出构成该三角形的三顶点Pi、Pi+1、Pi+2,并将Pi+1从数组空间中移除,同时以该三角形的起点Pi、终点Pi+2和下一个顶点Pi+3,构成新有向三角形△PiPi+2Pi+3并转步骤6;若有凹顶点,则转步骤5。
如图4所示,三角形内部是否含有凹顶点的判断,主要是将待定凹顶点D与三角形顶点Pi、Pi+1、Pi+2相连,则得到∠PiDPi+1、∠PiDPi+2、∠Pi+1DPi+23个角。若点D在△ABC内部或边上,即∠ADB+∠ADC+∠BDC= 360°,则三角形内部含有凹顶点;若点D在三角形ABC外部,即∠ADB+∠ADC+∠BDC< 360°,则三角形内部不含凹顶点。
步骤5将三角形△PiPi+2Pi+3的起点Pi存回数组空间,取出下一个顶点Pi+1,重新构成新有向三
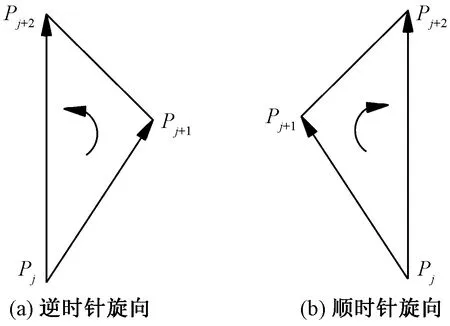
图3 三角形旋向的判定Fig.3 Judgment of triangle rotation
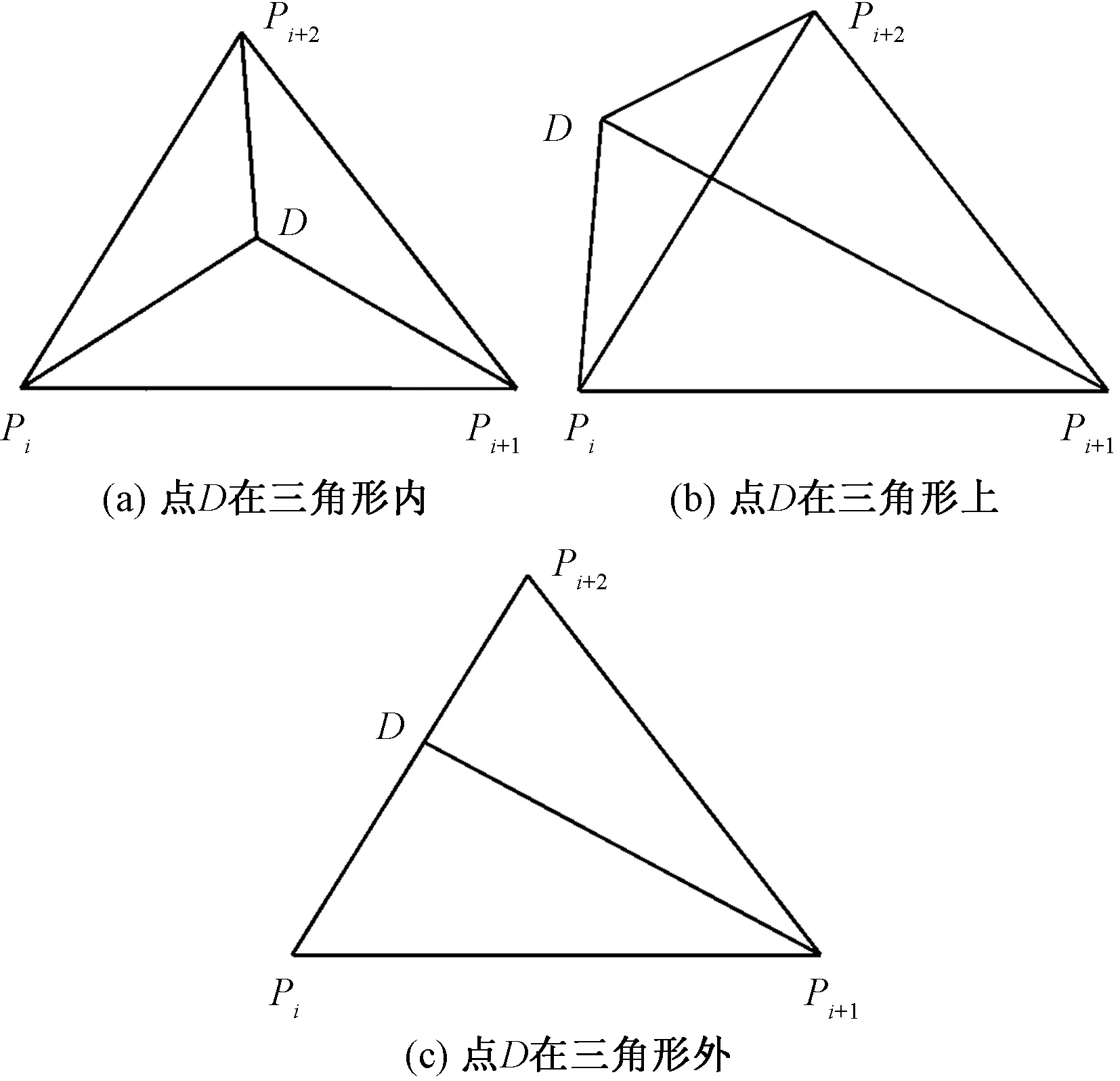
图4 三角形内部是否含有凹顶点的判定Fig.4 Judgment of the concave vertex inside the triangle
角形△Pi+1Pi+2Pi+3并转步骤6。
步骤6判断数组空间内顶点个数是否小于等于3,若是,则结束三角形网格划分,否则获取步骤4或步骤5中新构成的有向三角形,即△PiPi+2Pi+3或△Pi+1Pi+2Pi+3,再转步骤3进行旋向判断。
1.2.2 三角网格局部变换
为了使网格剖分的三角形形态最优,基于最小角最大准则[7]做网格进一步局部变换,即去除掉初始划分三角形的边界边,对剩余每条非边界边作以下处理:
步骤1遍历初始三角形网格,找出以非边界边为公共边的两个相邻三角形,并判断由这两个三角形所构成四边形的凹凸性。若为凹四边形,不作任何处理;否则转步骤2。
如图5所示,四边形凹凸性判断主要是将两相邻三角形的公共边记为直线l1,将两三角形中不在公共边上的两顶点所连直线记为l2。若直线l1与l2相交,则为凸四边形;反之为凹四边形。
步骤2计算两三角形中的6个内角并取出最小角α,再按照图6进行对角线交换,并计算两新三角形中6个内角的最小角β。
步骤3比较α、β两角大小。若α≥β,保留对角线交换前两三角形;反之保留对角线交换后两新三角形。
1.3 STL文件生成
为了获取轮廓相关信息,便于焊缝特征识别并避免应用范围的限制,对三维模型进行Delaunay三角剖分并生成STL文件。通过调用SolidWorks软件API函数,遍历三维模型的每个轮廓面,提取出每个
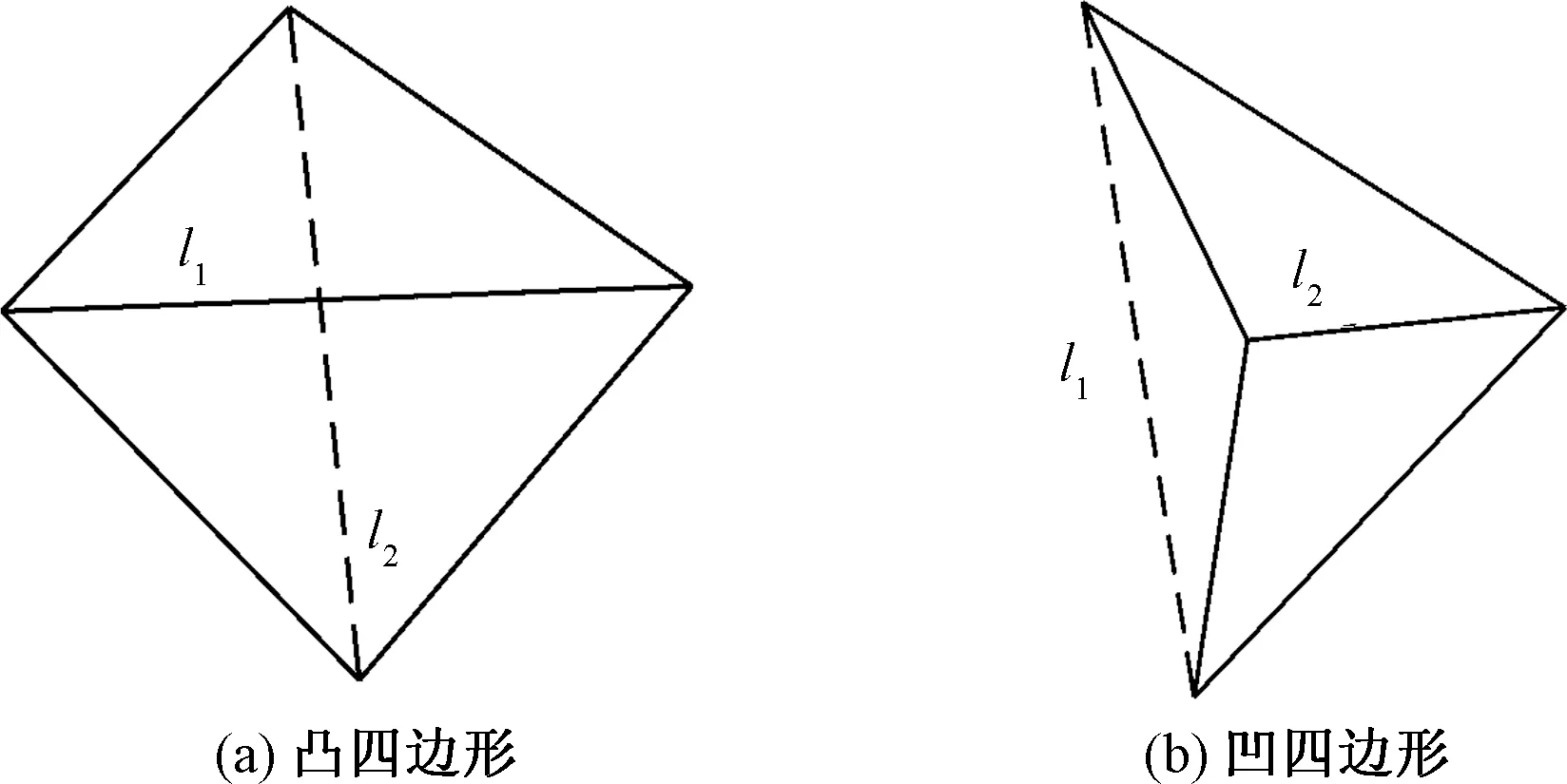
图5 四边形凹凸性的判定Fig.5 Judgment of concave and convexity of quadrilateral
图6 最小角最大化准则Fig.6 Minimum angle maximization criterion
轮廓面上的法向量(指向实体外部)和轮廓顶点坐标信息。将每个轮廓面的顶点按逆时针排列,利用上述三角网格剖分算法,将每次划分输出的3个顶点坐标作为三角面片的3个顶点坐标,三角面片的法向矢量为所在轮廓面的法向量,从而构成一个三角面片的几何信息。通过整个三维模型划分即可得到ASCII码文件格式的STL文件。
2 基于STL的焊缝特征识别
2.1 基本概念
焊缝特征[8]主要包括焊接接头形式和焊接坡口类型。接头形式通常可分为平接、角接、T型和搭接接头。坡口类型与接头形式直接相关,对于平接接头,常见坡口类型主要有I型坡口、V型坡口和Y型坡口;对于角接接头和T型接头,主要有不开坡口、单边坡口和双边坡口;对于搭接接头则常为不开坡口。文中针对4类焊接接头形式,共10种焊接坡口进行特征识别。
2.2 算法原理
焊缝特征识别主要基于三维模型的STL文件进行焊缝的接头形式和坡口类型识别,而两接头的待判定面位置关系直接影响接头形式。如图7所示,由于待判定面相对于坡口端面的面积较大,求出每个轮廓面面积并取最大的前四组,即可得到待判定面;然后根据待判定面处法向量(虚线)的平行或垂直关系进行4类接头的空间位置关系判别。
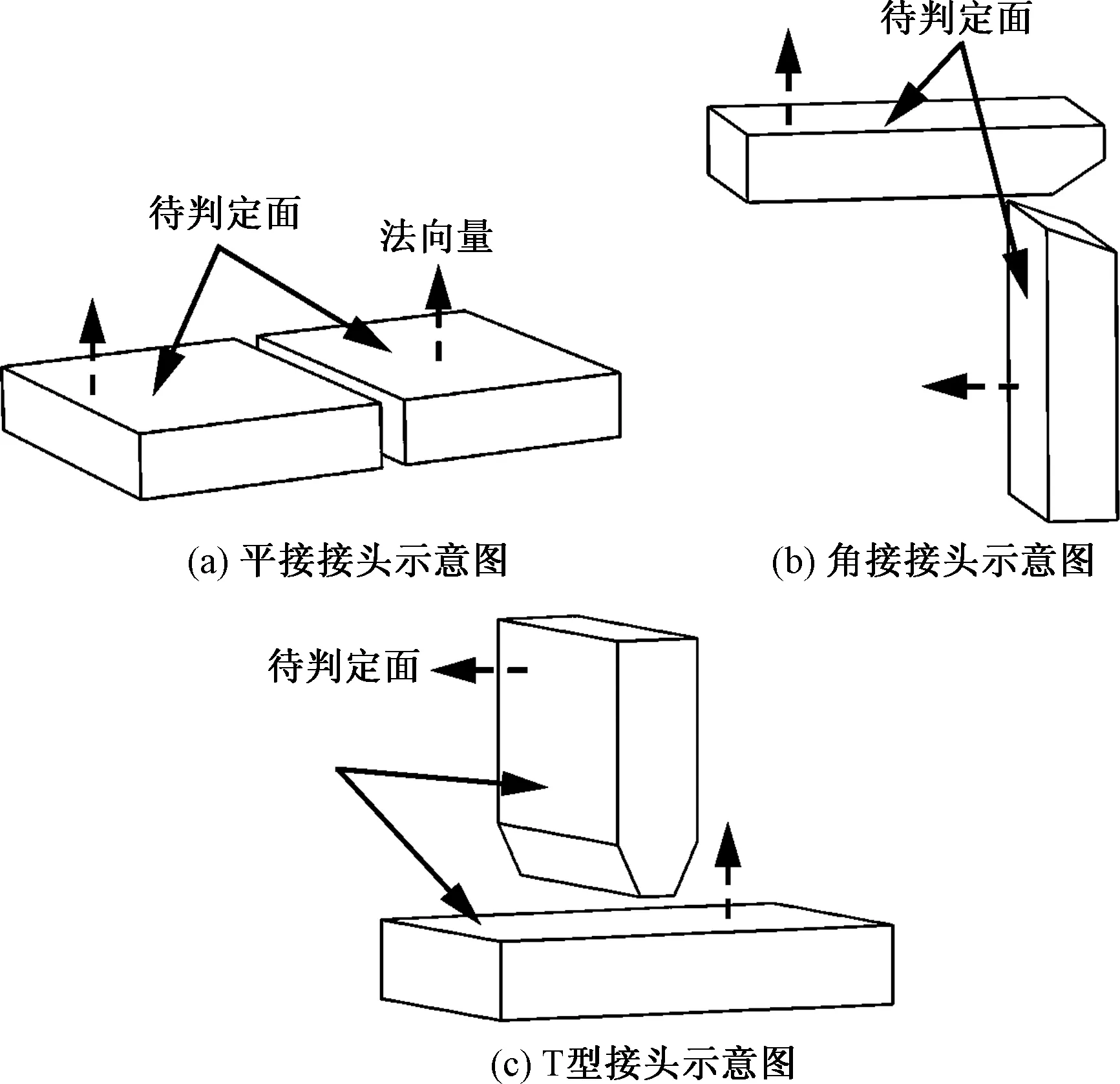
图7 待判定面示意图Fig.7 Surface to be judged
上述10种焊接坡口的轮廓线条数,通常可分为24条、27条和30条三大类。
当轮廓线条为24条时,主要有平接接头的I型坡口、V型坡口;角接接头的不开坡口、单边坡口;T型和搭接接头的不开坡口六种类型。图8(a)即属于24条轮廓线类型中平接接头所对应的V型坡口。此类型所涉及焊缝特征识别,主要是先取出前8组长度最短的轮廓线[图8(a)中数字1~8];然后针对该8组轮廓线,计算两两轮廓线的端点间所有距离;最后根据接头空间位置和最小轮廓线距离,进行接头形式和坡口类型的识别。
当轮廓线条为27条时,只有角接接头双边坡口和T型接头单边坡口。图8(b)属于27条轮廓线类型中角接接头对应的双边坡口。此类型所涉及焊缝特征识别,主要是针对10组最短轮廓线[图8(b)中数字1~10],并参照24条轮廓线中的相同处理方式,进行相应接头形式和坡口类型的识别。
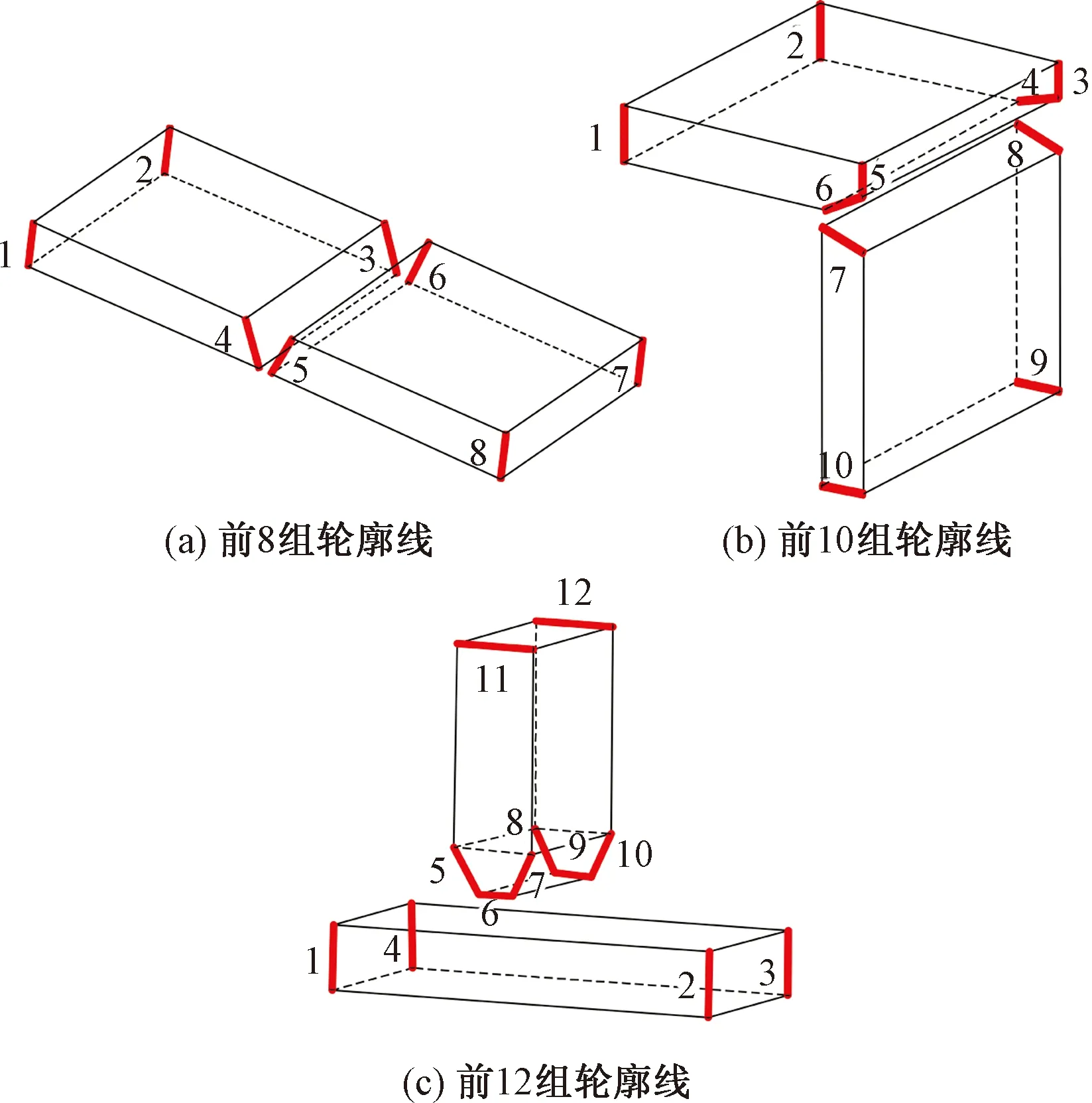
图8 轮廓线条选取示意图Fig.8 Schematic diagram of outline line selection
当轮廓线条为30条时,同样只有平接接头Y型坡口和T型接头双边坡口两种。图8(c)属于30条轮廓线类型中T型接头所对应的双边坡口。焊缝特征识别主要是针对12组最短轮廓线[图8(c)中数字1~12]并参照上述相同方式进行接头形式和坡口类型的识别。
2.3 算法描述
焊缝特征识别主要针对三角面片并基于海伦公式来实现,包括轮廓线及点提取;接头空间位置关系判断;接头形式和坡口类型的识别。
2.3.1 轮廓线及点提取
STL文件中所有的三角面片两两组合,对组合成的每一对三角面片进行以下处理。
步骤1判断一对三角面片是否存在两公共顶点?若是,则相邻;反之不相邻。对于相邻三角面片,则根据式(3)计算出两者的法向量夹角[9],并转步骤2;若不相邻,则取下一对三角面片继续本步骤的相邻判断。
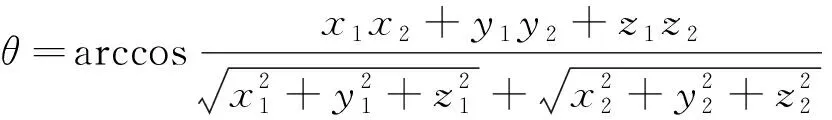
(3)
式(3)中:(x1,y1,z1)、(x2,y2,z2)为两三角面片的法向量。
步骤2根据法向量夹角确定两三角面片的公共线段是否为模型轮廓线。若θ=0或θ=180°,则两三角面片处于同一平面内,其两个公共顶点所组成的公共线段不是模型轮廓线;若0<θ<180°,则两三角面片处于不同平面内,公共线段是模型轮廓线的一部分。
步骤3输出步骤2中所有位于不同平面内的三角面片公共线段,即可提取到模型的全部轮廓。
步骤4统计各三角面片顶点在全部轮廓线条中出现的次数n。若n≥3,则该点为模型端点,进而获得所有轮廓顶点。
2.3.2 接头空间位置关系判断
步骤1基于海伦公式[10]计算STL 中三角面片面积,并求出每个轮廓面面积。取面积最大的前四组,并获取对应轮廓面的法向量。
步骤2根据式(4)对步骤1获取的法向量进行两两叉积并求出向量积的模长。若模长为0,则两个法向量平行。统计法向量出现平行的次数Pa。
a×b=(l,m,n)×(o,p,q)
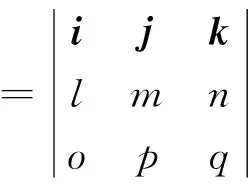
=(mq-np,no-lq,lp-mo)
(4)
式(4)中:(l,m,n)为轮廓面法向量a坐标;(o,p,q)为轮廓面法向量b坐标;i、j、k分别表示x轴正方向、y轴正方向、z轴正方向的单位向量,是空间向量的一组基底。
步骤3根据式(5)对步骤1获取的法向量进行两两点积并求出数量积。若积为0,则两个法向量垂直。统计法向量出现垂直的次数Vt。
a·b=(l,m,n)·(o,p,q)=lo+mp+nq
(5)
步骤4对步骤1中获取的法向量进行两两方向判断,并统计出方向相反的次数Op。
步骤5根据Pa、Vt、Op的值判断接头空间位置关系。若Pa= 6且Op=4,则两接头处于平行状态;若Vt=4且Op=2,则两接头处于垂直状态。
2.3.3 接头形式识别
步骤1根据轮廓线总条数获取各类最短轮廓线组。若为24条,则输出前8组长度最短的轮廓线组;若为27条,则输出前10组最短轮廓线组;若为30条,则输出前12组最短轮廓线组。
步骤2取次短长度的轮廓线作为距离阈值。针对步骤1中输出的最短轮廓线组,计算两两轮廓线的端点间所有距离,去除轮廓线本身长度后,将最小距离与距离阈值对比。若最小距离大于距离阈值,则称轮廓线距离为大间距;反之称为小间距。
步骤3根据接头空间位置和轮廓线距离进行接头形式识别。若接头处于平行状态,当轮廓线距离为小间距时,则为平接接头;反之为搭接接头。若接头处于垂直状态,当轮廓线距离为小间距时,则为角接接头;反之为T型接头。
2.3.4 坡口类型识别
步骤1根据轮廓线总条数和接头形式进行坡口类型识别。若轮廓线总条数为24条,当接头形式为平接或角接时,转步骤2;当为搭接或T型接头时,则接头都为不开坡口。若轮廓线总条数为27条,转步骤3。若轮廓线总条数为30条,转步骤4。
步骤2根据两条最小距离轮廓线的夹角α进行坡口识别。若接头形式为平接,当α=0时,则为I型坡口;反之为V型坡口。若接头形式为角接,当α=90°时,则为不开坡口;反之为单边坡口。
步骤3根据轮廓线距离进行坡口识别。若为小间距,则为角接接头双边坡口;反之为T型单边坡口。
步骤4根据接头形式和轮廓线距离进行坡口识别。若为平接接头且小间距,则为平接接头的Y型坡口;若为T型接头且大间距,则为T型接头双边坡口。
3 实验测试
3.1 三角剖分测试
为了验证文中船舶焊缝特征识别算法的有效性和稳定性,在CPU主频4.6 GHz、内存16 GB的PC平台上,使用Visual Studio 2019编程语言对“梳子”等多边形进行了剖分测试,并与单连通多边形环形追踪算法(单连通追踪法)[11]、基于凹凸顶点的三角剖分算法 (凹凸顶点剖分法)[12]和动态Delaunay三角剖分算法(动态Delaunay法)[13]进行了比较。4种方法两类多边形的剖分结果如图9和图10所示,剖分对比的性能指标采用网格平均质量系数qM和网格关联质量系数qJ[14]且定义如下,详细对比结果如表1所示。
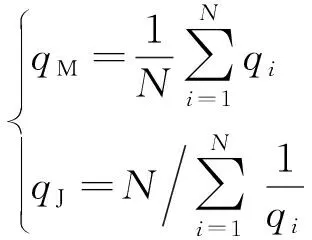
(6)
式(6)中:N为三角网格总数;qi=2r/R,其中r、R分别为三角形内切圆和外接圆半径。
由图9和图10可以看出,单连通追踪法中畸形三角形数量最多,网格形态较差,而文中算法畸形三角形数量较少与其相比有着明显优化。对“梳子”多边形划分时,动态Delaunay法无法剖分,而文中算法剖分测试正常且畸形三角形数量的控制也优于其余两种方法,剖分质量最好。由表1可知,无论是网格平均质量系数还是网格关联质量系数,本文算法的剖分质量都优于单连通追踪法、凹凸顶点剖分法和动态Delaunay法,且针对图9多边形分别平均增加了12.49%和12.78%,针对图10多边形分别平均增加了11.62%和11.74%,由此进一步说明本文算法畸变单元数较少,三角网格形态最优,这主要得益于基于三角形旋向的剖分和最小角最大准则的局部变换,有效降低了网格畸形程度,使得全体网格更接近于正三角形,保证较好网格质量的产生。
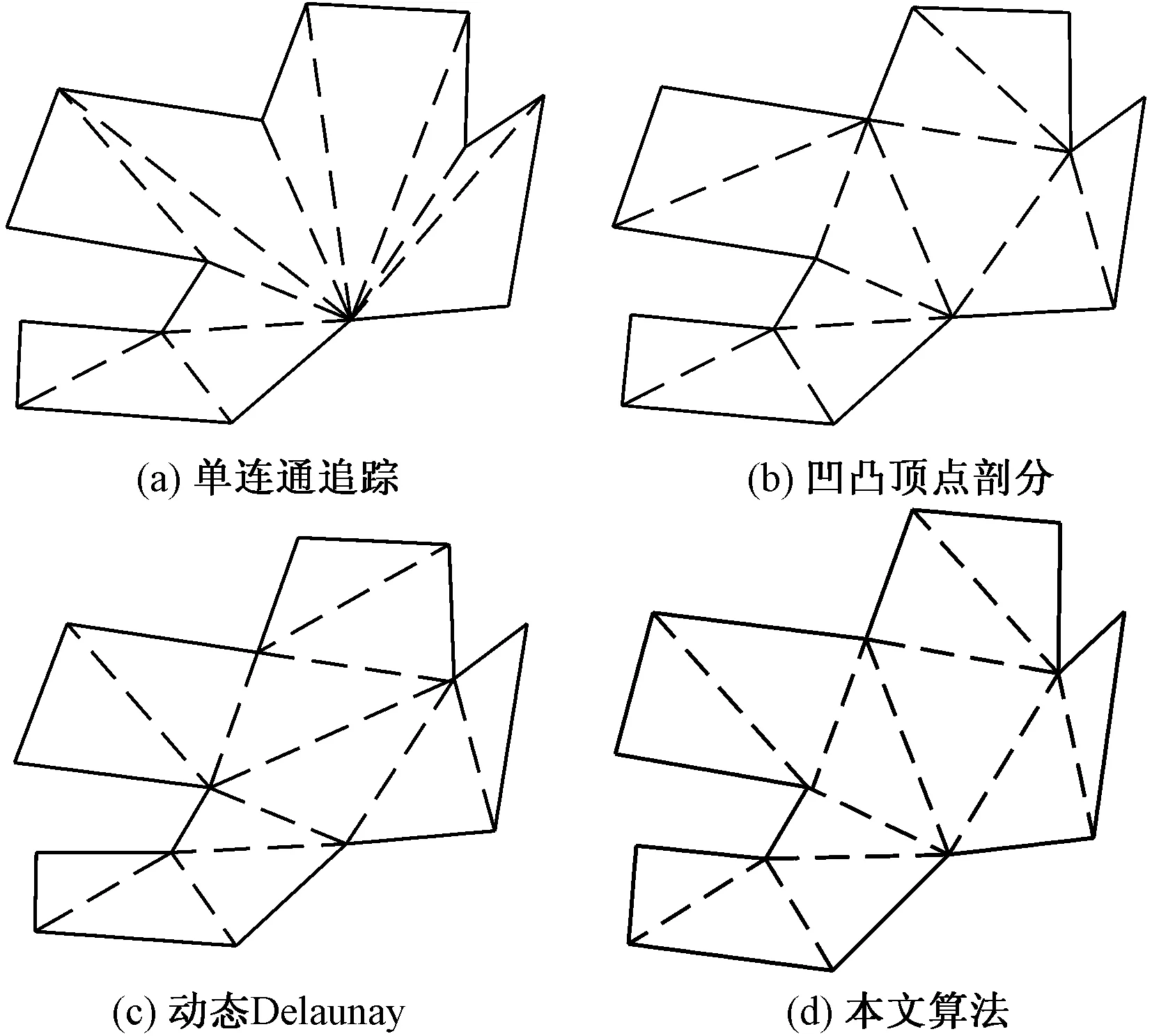
图9 4种算法剖分结果对比Fig.9 Comparisons of segmentation results of four algorithms
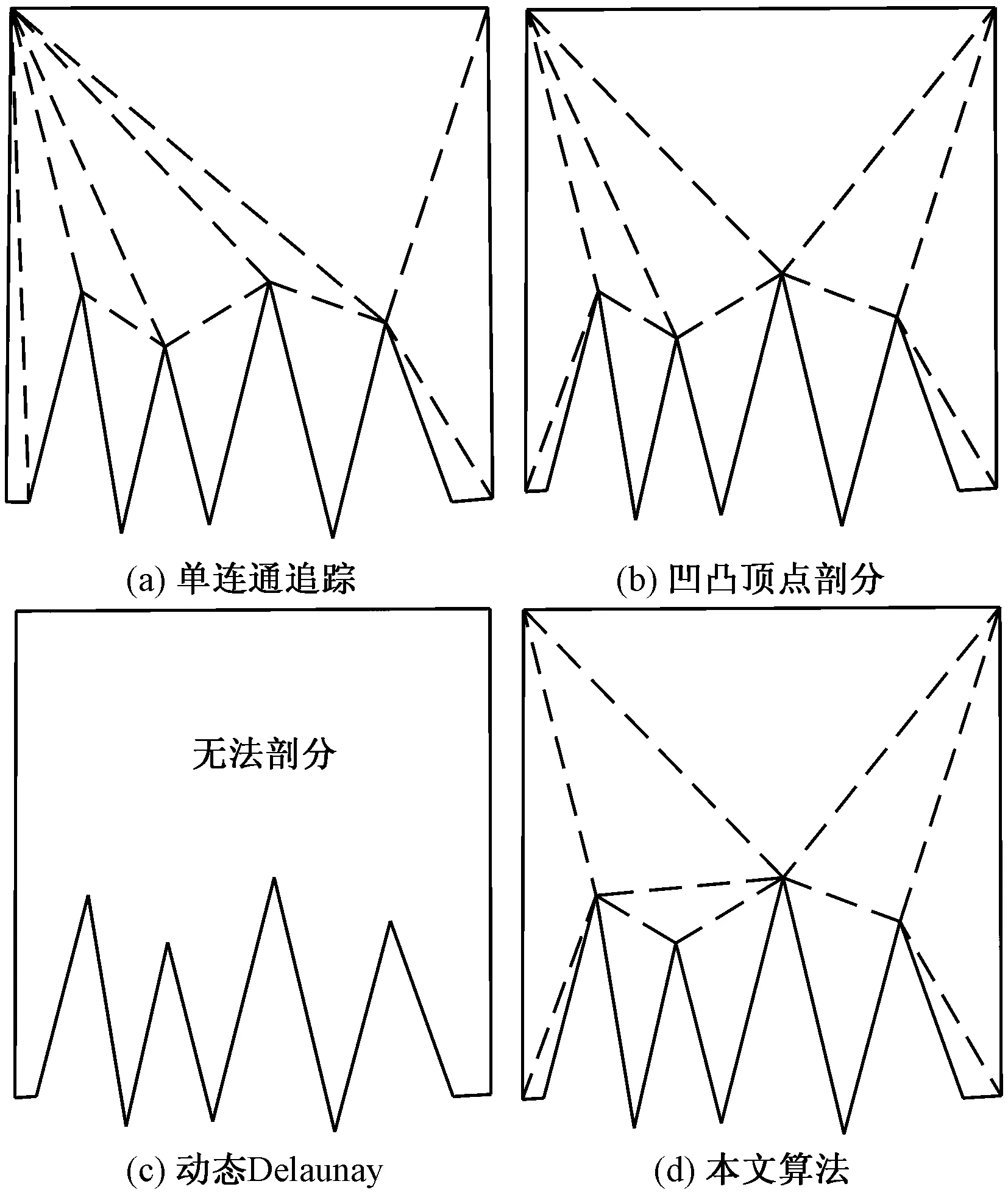
图10 “梳子”多边形三角剖分结果对比Fig.10 Comparison of “comb” polygon triangulation results
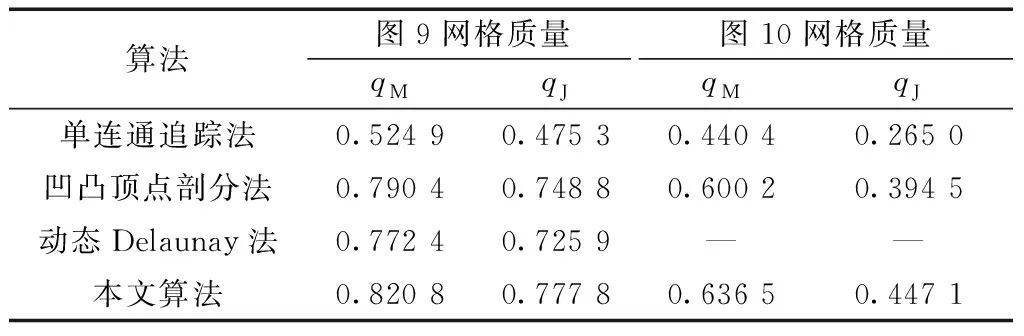
表1 网格质量分析
3.2 焊缝特征识别测试
为了进一步验证文中算法的有效性,针对图11中船舱段上的6处焊缝进行了特征识别测试,并与基于焊接特征的焊接工件库建模(特征库设计法)[15]和基于SolidWorks的遍历特征树技术(遍历特征法)[5]进行了比较。3种方法的对比测试结果如表2所示。
由表2可以看出,遍历特征法仅能识别出平接接头和T型接头两种形式,且对坡口类型无法识别,识别效果较差,同时受制于建模平台,应用范围有限。特征库设计法虽然与本文算法一样,都能准确识别出6处焊缝特征,但在接头和坡口识别的平均运行时间上均高于本文算法,执行效率低,此外,特征库设计法需要先对船舱段上的所有焊缝,进行特征造型设计并建立数据库,使得开发工作量大大增加,且当数据库规模较大在匹配焊缝特征时可能出现耗时较长的情况。而基于STL的焊缝特征识别算法在接头和坡口识别的平均运行时间上更短,执行效率更高,且只需获取模型焊缝的STL文件,前期处理量较小,同时识别的接头形式、坡口类型多,准确率高。
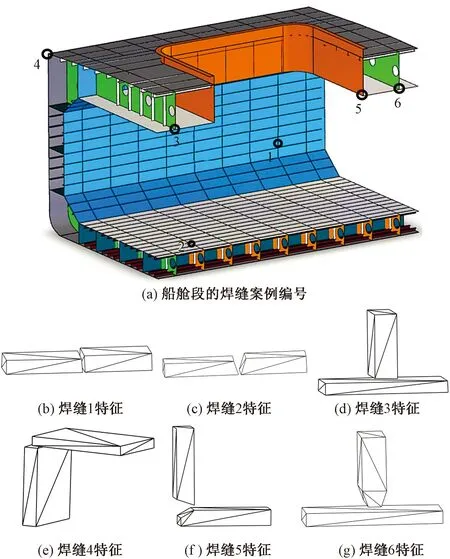
1~6为焊缝案例编号图11 船舱段的焊缝特征识别测试Fig.11 Recognition test of welding seam feature of ship cabin
本文算法的接头和坡口详细测试结果如表3和表4所示。可以看出,本文算法能快速统计出待判定面处法向量平行、垂直、相反的次数,精确获取最小轮廓线距离、距离阈值、轮廓线总条数和两条最小距离轮廓线的夹角,并根据关键参数作出正确判断和对比,准确识别出6处焊缝的接头形式和坡口类型,即平接接头I型坡口、平接接头V型坡口、T型接头不开坡口、角接接头不开坡口、角接接头双边坡口和T型接头双边坡口,从而实现焊缝特征的精确识别,执行效率高,验证了本文算法的有效性。
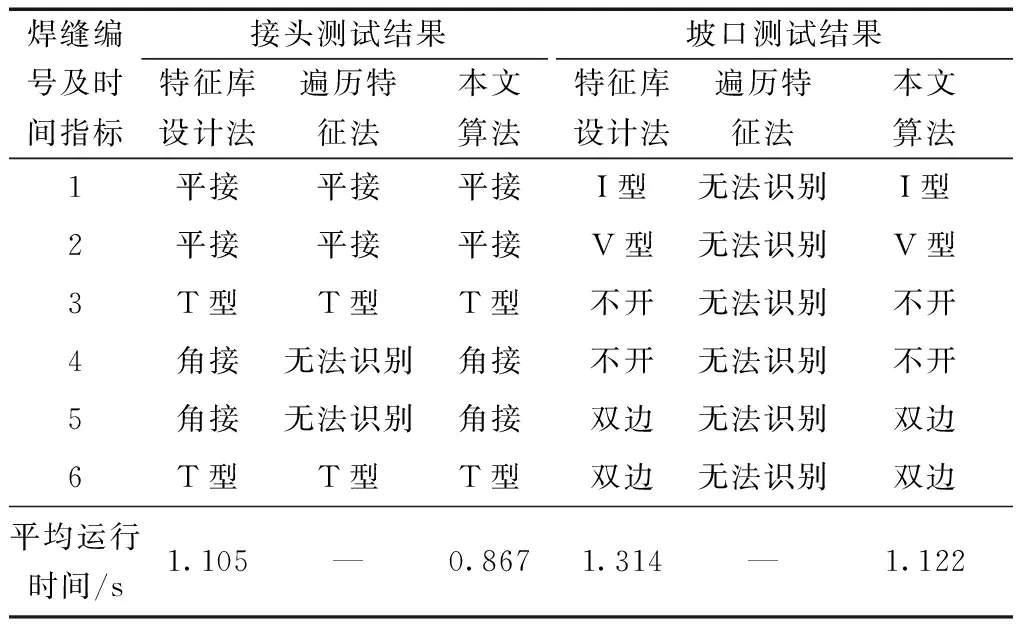
表2 3种方法测试结果
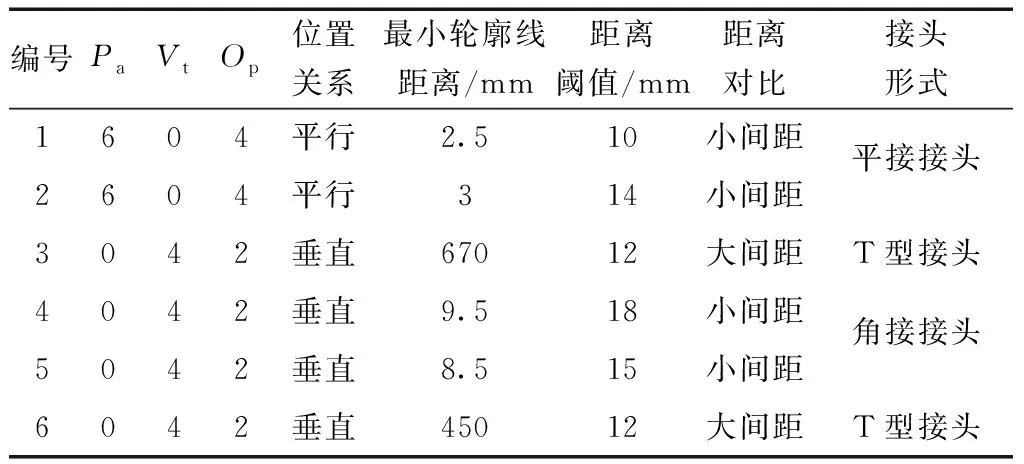
表3 接头形式测试结果
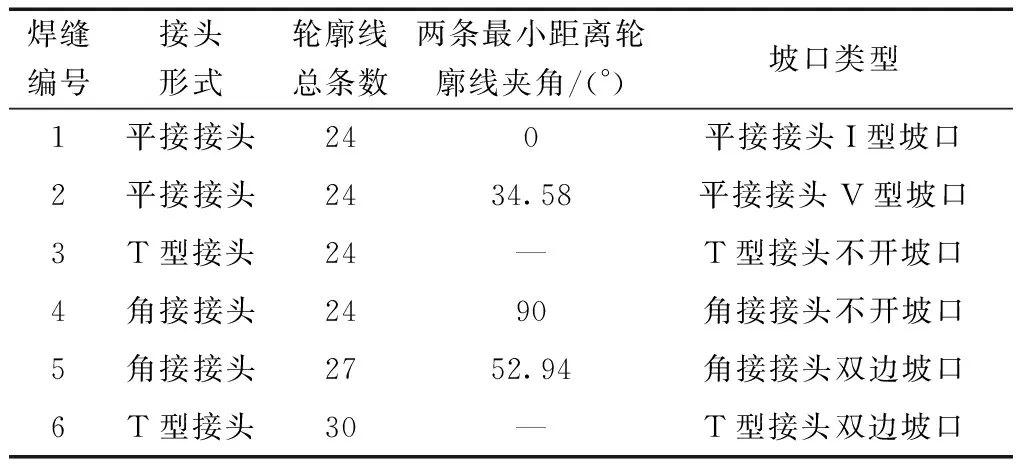
表4 坡口类型测试结果
4 结论
为解决目前焊缝特征识别单一、应用范围受限的问题,提出角剖分和轮廓分析的船舶焊缝特征识别算法。根据测试结果得出以下结论。
(1)基于三角形旋向的Delaunay三角剖分,能实现对特殊复杂多边形的快速三角剖分;角系数法能有效地获取每个顶点的凹凸性,剖分生成的三角形态较优,执行效率高,有利于STL文件的获取。
(2)基于相邻三角面片的法向量夹角,能快速提取出模型的轮廓线及点;待判定面处法向量能正确实现接头空间位置关系判断;根据轮廓线总条数和最小轮廓线距离,能准确识别4类接头形式和10种坡口类型。
(3)基于STL的焊缝特征识别算法,识别的接头形式和坡口类型多、准确率高,大大提高了算法的实用性、广泛性。
测试结果表明本文算法具有多边形剖分质量较好、焊缝特征识别精确的优势,为船舶焊接机器人快速、准确选择焊接工艺参数,提高焊接质量和效率提供了保障。
