树结构组套索人脑超网络构建与分类

闻敏， 刘永艳， 李瑶， IBEGBU Nnamdi Julian， 郭浩

(太原理工大学信息与计算机学院， 晋中 030600)

由世界卫生组织2020年的调查统计得知，全世界已有3.5亿人为抑郁症患者，根据相关新闻报道，每年有1%～6%的抑郁症发病率[1]，抑郁症患者人数逐年上升，抑郁症已成为危害人类健康的第二大杀手，其症状为情绪低沉、兴趣衰减、行动积极性下降。在中国，抑郁症还未被列入门诊医疗保险慢性疾病的范畴，高额的心理咨询费用也未被归入医保报销领域。抑郁症不仅会对患者的身心造成极大的伤害，势必也会对患者的家庭造成不小的经济压力。近年来，全球性的抑郁症患者比例的大幅度上升引起了世界各国的精神疾病研究人员的关注。由于精神疾病影响大脑的认知功能，而神经成像的宗旨也是在对精神疾病患者与正常人的大脑图像进行分类。而这能够在不同脑区之间的连接中确定精神疾病患者大脑的变化。脑区之间的连接是由神经成像数据，例如磁共振成像(magnetic resonance imaging，MRI)技术产生的,并使用功能、结构或形态网络[2]表示。

对于现有的研究，许多方法被提出来用从静息态功能磁共振成像(functional magnetic resonance imaging，fMRI)技术获取的数据上进行脑网络建模，如基于相关[3]的方法，基于稀疏[4]的表示方法等。而以上所提出的脑功能连接模型反映出脑区之间信息传递的二阶关系。随着功能性脑网络研究的发展，有研究表明大脑区域之间的联系，不仅是两个脑区之间的信息传递，同样包含大脑区域的多个脑区之间信息的高阶传递。针对研究与抑郁症相关的生物标志物，这种传递的高阶信息对于提高识别抑郁症的准确性至关重要。为此，一些研究人员开始使用超网络来描述脑网络[5]。

超网络是基于超图理论发展而来的，是图的延伸，在超网络中，一个脑区对应一个节点，多个脑区构成一条超边，即在大脑区域内，多个脑区进行信息传递作用。然而目前大多数的超网络的构建方法均是利用套索(least absolute shrinkage and selection operator，Lasso)[6]方法进行超网络建模。然而Lasso的L1范数存在每个变量都是独立估计的缺点，因此没有考虑变量之间的关系和结构。研究人员更希望所有相关的脑区被作为一个组来选择[7]。假定脑区分组为可用的先验知识，并且它是以整组而不是用单个脑区作为变量选择的单位。但该方法仅能在组级上选择变量，缺乏选择组间变量的能力，对于组套索来说它被扩展到一个更一般的设置[8]。在稀疏模式上有各种更复杂的结构，而不是简单的分组信息。然而研究表明，生物信息领域不仅存在重叠组的情况(即某种功能可由多个脑区共同协作来实现，且某一脑区在同一时间下参加多种特定功能)，还存在复杂的树组结构问题[9]。为了解决这个问题，本研究考虑了大脑区域中的树组结构问题，并引入了树结构组套索方法来改进超网络的构建。

为了增强组间差异表征能力，以准确地发现生物标志物以及疾病的病理机制，现提出利用树结构组套索方法构建脑功能超网络，力求创建更有效及更可靠的超网络模型。该方法属于层级树结构，包括根节点(所有脑区)，中间节点(对脑区进行分组)以及叶子节点(组中高度相关的一些脑区)。既可以通过事先定义分组，也可以事先对每组进行细划，相当于组级以及组间都采用了预设组进行划分，还可以解释组间的覆盖情况。

主要工作包括：①利用树结构组套索的方法进行脑功能超网络建模；②利用超网络定义的三个局部聚类系数对构建的脑功能超网络进行特征提取；③利用KS(Kolmogorov & Smimov)[10]非参数检验方法选取局部聚类系数指标间显著性差异的特征；④使用支持向量机(support vector machine, SVM)[11]对显著性差异特征进行分类，提供更准确和相关的成像标记。

1 材料和方法

研究可分为以下几个流程进行：数据采集及预处理、使用基于树结构组套索的方法进行脑功能超网络建模、计算三个不同定义的聚类系数进行特征提取、采用非参数检验方法选择最具差异性特征以及采用SVM方法进行分类。研究流程如图1所示。

MDD表示抑郁症患者；NC表示正常人；AAL表示自动解剖图1 研究流程Fig.1 Research flow chart

1.1 材料与分析

1.1.1 被试信息

被试数据在山西医科大学第一附属医院的放射科医生在严格遵守山西医学伦理委员会(编号：202013)和赫尔辛基宣言要求的情况下采集完成，并且数据采集工作之前，严格遵守汉密尔顿量表(Hamilton depression rating scale，HAMD)的规定，征得被试及其法定监护人的同意，和每位被试签订书面协议。实验研究对象包括38名第一次发病，且未服用过药物的抑郁症患者(major depression disorder，MDD)和28名正常对照组(normal control，NC)，总共66名被试。研究所有的被试均使用西门子3T系统进行功能磁共振(fMRI)扫描。被试的具体数据信息如表1所示。

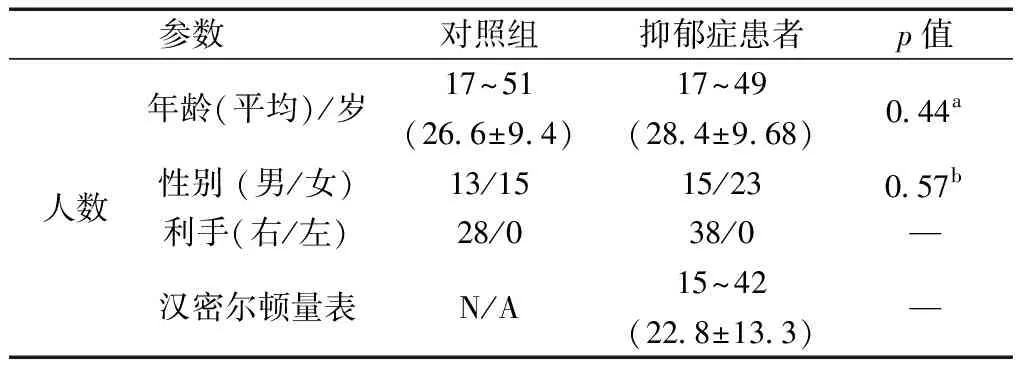
表1 被试的具体信息Table 1 Specific information of participants

1.1.2 数据采集和预处理

为了保证数据的准确性，在扫描过程中，采用软海绵将被试的头部固定住以防因被试头部晃动而产生数据误差。除此以外，被试者要求在扫描过程中轻闭眼睛，脑部呈放空状态，但不能陷入昏睡并保持思维清晰。实验扫描参数设置如下：回波时间为30 ms，射频重复时间为2 000 ms，层厚为4 mm，层间间隔为0，视野范围为192 mm×192 mm,翻转角为90°，存储矩阵为64 mm×64 mm。

数据处理在MATLAB平台环境下进行，且本研究利用SPM8 (http://www.fil.ion.ucl.ac.uk/spm)来完成本实验的数据预处理工作。对于每一名被试，数据预处理步骤如下：由于fMRI信号的不稳定，每名受试者的前10卷功能时间序列会被丢弃。在对数据样本采集时需要时间层校正和头动校正，即除去超出允许头动范围的被试数据，头动允许范围为头动小于等于3 mm且转动小于等于3°，最终有2组抑郁症及正常对照组数据因超过头动允许范围被丢弃，即最终得到66例被试数据。随后，将图像通过仿射变换标准化为3 mm×3 mm×3 mm2的蒙特利尔神经研究所(montreal neurological institute，MNI)标准空间中。

1.2 超网络构建

1.2.1 稀疏线性回归模型

采用稀疏表示[12]方法，利用 rs-fMRI时间序列构建成脑功能超网络。首先通过自动解剖标记(anatomical automatic labeling，AAL)[13]模板将大脑区域分割为90个感兴趣解剖区域(regions of interest，ROI)，每个脑半球被均分为45个ROI，每一个ROI可被定义为脑网络中的一个节点。在构建超网络之前，需要提取各脑区的时间序列信号。其次，白质信号、头动校正以及平均脑脊髓液(cerebro-spinal fluid，CSF)对信号的影响巨大，为减小实验的误差性，需要对每个脑区的平均时间序列进行回归分析；最后，根据计算得到的残差来构建脑功能超网络。

稀疏线性回归模型具体表示为

(1)

1.2.2 基于树结构组套索方法进行脑功能超网络建模

标准的Lasso方法假设所有的特征都是独立的，但这并不适用于真实的特征是复杂关联的情况。具体来说，研究表明脑区间经常协同工作来实现某种功能[14]，因而套索方法缺乏组效应的解释能力。鉴于脑区间存在的组结构问题，已有的研究针对群体结构问题引入了分组的方法模型[15]，如弹性网(elastic net)方法、组套索(group Lasso，gLasso)[16]方法。但弹性网方法存在的主要问题之一是依据数学公式自动选择组，缺乏脑区间组结构先验知识的表达。基于此，组套索解决了自动组选择效应的问题，也就是可以人为事先定义分组情况，但该方法仅能在组级上选择变量，缺乏选择组间变量的功能。因此稀疏组套索(sparse group Lasso，sgLasso)方法[17]被提出用来改善脑功能超网络的构建。该方法实现了能在组级和组间自由选择变量的功能，但这种方法在选择组间变量时是依据数学模型自动选择组中一些脑区，认为与所选脑区存在信息交互。为了提高特征选择的性能，有必要获取模型中特征之间的结构关系。

图2 树组结构示例图Fig.2 Example diagram of tree group structure

为了体现出树形结构的层次空间关系，在进行超网络建模之前，先使用K-means[18]聚类方法将所有脑区聚类为K组，即树的第二层每个节点代表对脑区进行聚类操作得出的一个分组，每个叶子结点代表组中高度相关的脑区。随后进行树结构组套索方法的超网络模型建模。

正则化目标函数优化模型为

(2)

1.3 特征提取

在得到了由树结构组套索构建的脑功能超网络之后，要对已构建好的脑网络拓扑进行特征提取，用以分析网络属性。本实验的特征提取由3个指标的计算组成，而这三个指标的计算为三个不同定义、不同关系的聚类系数[21]。从目前已有的研究中可以看出，聚类系数在很大程度上被用来评估超网络局部属性的性能。有关公式为

(3)

(4)

式(4)中：HCC2(v)为与节点v相连的邻居节点的数量；N(v)为超边中包含节点v及其相邻节点的集合。如果∃ei∈E且u,t,v∈ei，则I′(u,t,v)=1。

(5)

式(5)中：HCC3(v)计算超边之间的重叠量，即指节点v的相邻超边，邻居区域的密度由邻居区域的超边重叠量来表示；|e|为超边中包含的节点数目；S(v)表示超边的集合，在这些超边中都包含节点v，S(v)={ei∈E:v∈ei}。

1.4 特征选择与分类

特征选择是机器学习中最常见的问题之一，其目的是选择最具判别性的特征进行分类和预测。从已构建好的脑功能超网络中提取出270个特征，但这些特征并不都是最具差异性特征，它可能会存在不相关或者虚假的属性，因此要选取最具显著性差异的特征并将其成功应用于分类。具体地说，分别对由根据抑郁症患者和正常对照组这两种被试构建出的脑功能超网络中分别进行HCC1、HCC2、HCC3局部属性指标计算，随后将得到的270个节点属性特征由已通过伪发现率(false-discovery rate，FDR)(q=0.05)[22]方法矫正的Kolmogorov & Smimov nonparametric test进行组间非参数检验，最后经由KS检验方法得出的每个被试的p<0.05的最具差异性特征，随后将选取的特征用于分类。

在完成特征选择以后，以选取的最具显著性的差异特征作为分类标准构建分类模型，由此实现有效分类。因而在将分类特征进行分类前，需将具有显著性差异的特征选择出来，并将其计算得出它的算术平均值与标准差，降低因数据的不精确而导致的实验误差性，以此来提高分类准确率。分类问题作为机器学习下的一个重要问题，是为了对已有类标签的训练集数据展开训练，构建相应的分类模型。在实验分类过程中，使用SVM作为分类器，并使用脑网络建模方法中常用的径向基函数(radial basis function, RBF)作为核函数，并采用留一交叉验证方法对分类模型的性能进行验证。

2 实验和结果

2.1 差异性脑区

为探究精神疾病大脑区域发病的病理机制，从抑郁症患者和正常人的大脑区域中提取出差异性脑区。首先计算由树结构组套索方法构建的超网络得到的三个局部聚类属性指标，并用KS非参数检验方法对其做分析研究，本方法下共得到10个MDD与NC之间最具显著性差异的脑区，它们分别是：是右侧眶部额上回(ORBsup.R)、右侧补充运动区(SMA.R)、左侧眶内额上回(ORBsupmed.L)、右侧眶内额上回(ORBsupmed.R)、右侧海马旁回(PHG.R)、左侧楔叶(CUN.L)、右侧缘上回(SMG.R)、右侧尾状核(CAU.R)、左侧豆状壳核(PUT.L)、左侧颞横回(HES.L)。选择出来的最具差异性脑区在目前已有的关于抑郁症分类研究中已得到充分验证。康嘉慧等[23]研究证明了与健康对照组相比，青少年抑郁症患者的右侧眶部额上回的低频振幅(amplitude of low frequency fluctuation，ALFF)值显著升高。王利娟等[24]研究证明患有睡眠障碍的抑郁症患者与健康对照组相比在右侧补充运动区的局部一致性(regional homogeneity，ReHo)值显著增加。Ying等[25]研究证明晚发性抑郁症(late-onset depression，LOD)原发性病变的ALFF广泛分布于左侧眶内额上回。李璐莎等[26]研究证明与健康对照组相比，抑郁症患者的右侧眶内额上回的ALFF值在降低。Rolls等[27]研究证明了与未用药的抑郁症患者相比，接受药物治疗的抑郁症患者的海马旁回的功能连接性较低。Peng等[28]研究证明了焦虑性抑郁症患者的左侧楔叶的灰质体积大于健康对照组。Chen[29]等研究证明了与健康对照组相比，伴有抑郁症的早泄患者右侧缘上回的淋巴结参与减少。Filip等[30]研究证明了右侧尾状核区域的灰质体积的增加与核心评估分数显著相关。王智等[31]研究证明了与健康对照组相比，刺激前治疗难治性抑郁症患者的左侧豆状壳核的功能连接较高。Hall等[32]研究证明了与健康青少年对照组相比，患有重度抑郁症的青少年在左侧颞横回区域中看到可怕的面孔时具有较低的激活性。通过树结构组套索方法构建的脑功能超网络选取的MDD与NC之间最具差异性的脑区名称及p值对应表以及使用BrainNet软件将最具差异性脑区映射到皮质表面的分布图分别如表2及图3所示。综合分析看，本研究提取到最具差异性脑区与之前的研究结果基本一致，对抑郁症诊断有着重要的意义。

2.2 分类表现

为有效研究新方法的性能优劣，基于树结构组套索方法构建出的脑功能超网络通过准确率、敏感度、特异度以及BAC(balanced accuracy)这四个方面来评估所建的模型的分类性能。分类准确率定义为抑郁症患者及正常对照组可以被正确分辨的概率；灵敏度定义为抑郁症患者可以被成功分辨为抑郁症病人的概率；特异度定义为正常对照组可以被成功分辨为正常人的概率。为避免由数据集不平衡导致的膨胀性能[33]，将敏感度和特异度的算术平均值来表示BAC，以此来减少实验的误差性。

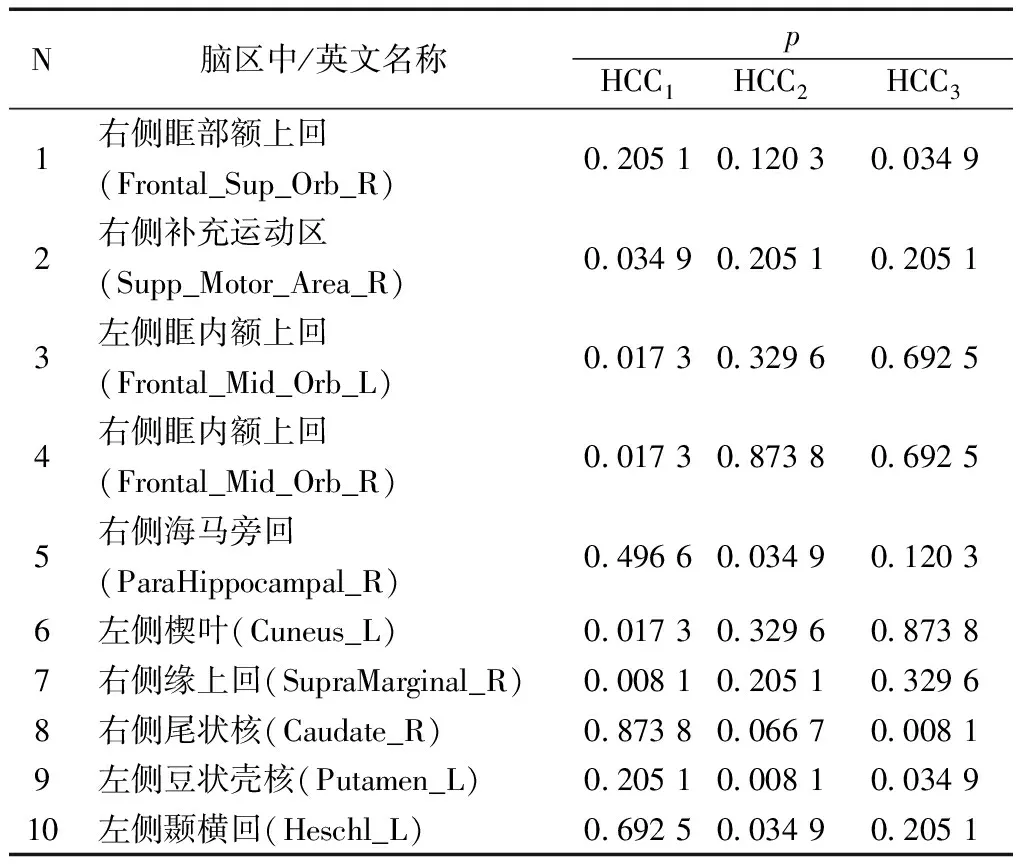
表2 显著差异脑区及其p表Table 2 Table of significantly different brain regions and their p

图3 差异脑区分布Fig.3 Differential brain area distribution

综合评估了该研究所述的方法构建的超网络的分类性能，并结合传统的脑网络的构建方法、套索方法、弹性网方法、组套索方法以及稀疏组套索方法进行了对比分析的实验。由于本方法具有预设组效应，在对超网络建模以前采用的K-means聚类方法进行分组时具有随机性，为了保证避免在对脑区分组时出现因分组随机性而导致的实验结果产生误差，在每个实验分组下分别以相同的操作重复做了50次实验，随后将每组实验的结果进行算术平均运算得到均值作为实验的最终结果进行对比分析。为了对比出基于本方法进行的脑功能超网络建模和其他方法之间的差异性，本研究仅使用三种聚类系数进行特征选择以及使用RBF核函数的分类方法，不同脑网络的构建方法以及新的超网络建模方法的分类结果如表3所示。结果表明，树结构组套索方法下的分类性能要高于传统的脑网络构建方法、套索方法、弹性网方法、组套索方法以及稀疏组套索方法。

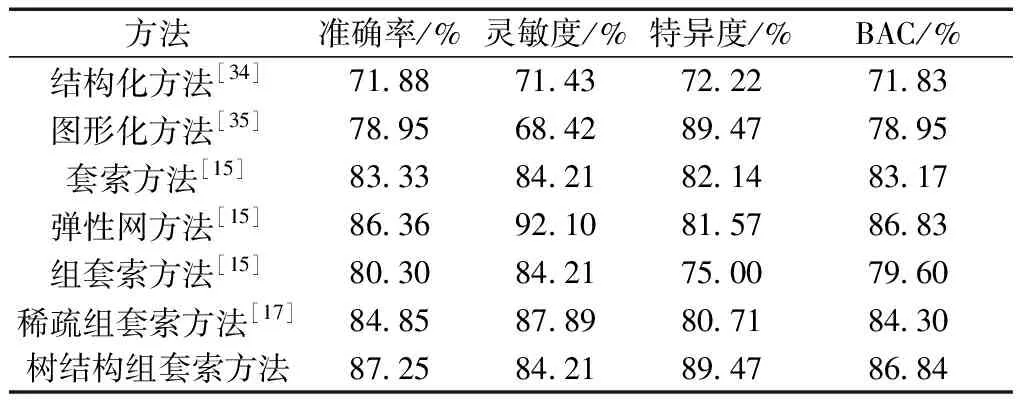
表3 各方法的分类表现对比Table 3 Comparison of classification performance of each method

3 参数讨论

参数调优在整个实验过程中是一项不可或缺的环节，参数的选择会对实验的最终结果造成不可忽视的影响。在本研究中，主要涉及在树结构组套索方法下构建的超网络选取的聚类数K和正则化参数λ对于最终的分类效果的差异性。为了分析这两个参数对于抑郁症患者和正常对照组之间分类效果的影响，以树结构组套索进行超网络建模构的方法进行了对比分析实验。

3.1 聚类参数K的影响

为了体现出预设组的效应，本实验在创建超边前实选用了K-means[17]聚类算法进行聚类。参数k为在基于树结构组套索方法下构建脑功能超网络的分组数。分组数K值的选择会影响到使用该方法构建的网络拓扑结构同时也会对最终的分类结果产生影响。

为了探究分组数K对构建的网络模型产生的影响，将聚类参数k的取值范围设置为[3,90]，步长间隔为3，总共30组实验，在每一组的实验下构建树结构组套索方法的脑功能超网络。根据聚类算法的特性，它在每次的聚类过程中都会进行一次中心点的移动，它会将中心点移动到每一次划分的包含其他节点的平均位置上。因而在本部分的实验，分组数K的选取具有不确定性，聚类的结果会因分组数K的选取而随之改变，进而导致该方法构建的网络拓扑结构及其最终分类结果产生不稳定的差异性。为了确保实验的准确性，在每个实验分组K下进行了50次实验，并对每组实验的结果求其均值作为该组的最终结果，最后将各组的实验结果进行比对分析。如图4所示，当K=57时，有最高的分类准确率，达到87.25%。

图4 聚类参数k对应的分类结果Fig.4 Classification result of clustering parameter k

3.2 正则化参数λ的影响

构建树结构组套索脑功能超网络时通过设置λ来控制模型的稀疏度，即不同的λ会产生不同的超边，进而产生不同的分类效果。采用升序的组合方法，共测试9组λ，它们分别为{0.1}, {0.1,0.2}, {0.1,0.2,0.3}, …, {0.1,0.2，…,0.9}，分别采用这9组λ进行网络建模，并选取最具判别性特征并进行分类。分类结果如图5所示，结果表明，在λ采用{0.1,0.2，…,0.9}时，有最高的分类准确率，为87.25%，表明分类准确性可能随着λ个数的增加而提高。

图5 正则化参数λ对应的分类结果Fig.5 Classification result of regularization parameters λ

4 结论

近年来，静息态脑功能超网络已广泛应用于脑部精神疾病的分类研究中。脑病变并非严格集中在一个地方，其周围区域也有助于临床诊断。现有的超网络建模方法在进行超网络构建时不能有效考虑层次组结构问题。鉴于这个问题，提出树结构组套索方法构建超网络。可以通过事先定义分组，即对组级以及组间都采用了预设组进行划分，并可以对组间的重叠性做出解释。结果显示树结构组套索方法下得到的分类效果要优于其他方法，能更好地体现人脑中复杂的层次组结构关系。

尽管在目前的研究中，实验已取得较好的结果，但仍存在局限性。首先，在构建模型之前采用K-means聚类方法进行分组时具有一定的随机性，即使求取多次实验结果的均值来减小误差，但仍给实验结果带来一定的影响；其次，考虑到抑郁症患者的隐私性问题，实验的数据采集具有一定的难度，因而本实验采用数据集的受试者数量较少。以上的几个局限问题有待于日后的研究来改进。