基于空铁联运的延误旅客行程恢复方法
2022-11-04陆溪邵荃
陆溪, 邵荃
(南京航空航天大学民航学院, 南京 211106)
随着经济发展与人民生活水平提高,航班准点率越来越难以满足旅客要求,导致了航空旅客的流失。且延误恢复过程中存在着可选方案单一的问题,旅客通常只能被迫接受航空公司的行程安排,出行体验感不佳。近年来中国高铁网络不断完善,其在短途线路中表现出的便捷、准点等优势恰巧能够弥补民航运输的短板,给民航带来了竞争压力。为了将二者之间的竞争转化为合作,空铁联运的概念由此提出并受到了广泛关注。航班和高铁班期密度的增大,提供了更多空铁衔接的机会;市内轨道交通和综合交通枢纽等基础设施的完善,为空铁合作提供了良好的实施基础。由此可见,航空与高铁协同解决实际延误问题的方法已具备了较为成熟的实施条件,能为航班延误恢复带来新的解决思路。
目前国内外学者已对延误恢复问题进行了深入研究。宾云鹏等[1]考虑航班恢复公平性约束,构建机场航班计划恢复模型。Suh等[2]运用大型邻域搜索启发式算法进行延误后航班管理,以实现机场停运后旅客的快速转移。顾兆军等[3]建立了一种基于旅客类别的旅客行程恢复模型,通过旅客优先级确定其恢复序列,从而改善航空公司品牌信誉。Hu等[4]考虑了不同延误场景下的旅客恢复意愿,设计启发式变领域搜索算法对问题进行求解。至于空铁联运方面,王淑伟[5]提出“干线民航+轨道交通”的高质量综合运输模式,促进航空公司和高铁部门结成利益共享原则下的共同体。徐凤等[6]对空铁联运网络进行研究,建立网络模型并设计基于遍历搜索的最短路径算法进行求解。Wang[7]通过构建双层航空高铁耦合网络描述市内换乘过程,并通过实例验证城市内部的多运输模式可达性。吴明昊等[8]建立了上层空铁联合运输服务网络和下层客运路线选择的双层优化模型。Marzuoli[9]详细阐述了采用多种交通方式协同进行航班恢复的方法,并提出了实施建议。牟振华等[10]基于效用理论构建旅客出行选择博弈模型,探究旅客“空铁抉择”的动态演化过程。吕宗磊等[11]针对枢纽机场拥堵问题,在枢纽航线网络基础上引入高铁线路建立优化模型。
针对旅客行程恢复的问题,已有学者提出运用空铁联运方法拓展恢复策略,但大多只停留在理论层面,对于实际应用中模型和实施方法的研究较少。航班延误研究大多针对飞机和机组资源,研究旅客行程恢复的较少。因此,现构建空铁耦合的时空拓扑网络,在此基础上建立旅客行程恢复模型,并设计旅客行程搜索算法。最后通过模拟延误情境,对比验证考虑空铁联运恢复模型的正确性和有效性,并分析空铁衔接时间限制对恢复方案性能的影响。
1 空铁联运时空拓扑网络
1.1 网络描述
高铁与航班具有独立的线路网络,本身没有直接联系,但旅客在两运输方式之间的换乘使得双层网络间产生了映射关系。考虑到旅客行程恢复问题的重点在于城市间的转移,故忽略城市内部的空铁换乘行为。将城市内部的高铁站点和机场统一用其所在城市节点代替,从而实现双层网络的耦合,生成空铁联运拓扑结构网络。
为更好地描述旅客行程时间信息,在此基础上引入时间性。此时构建的时空拓扑网络不仅可以直观反应该延误情境下城市间的空铁连接情况,还可以通过城市节点的班期时刻信息对延误时间进行描述,从而为后续模型中延误损失的刻画提供依据。
1.2 网络构建
用G=(N,E)表示构成的拓扑集联网络,其由城市节点集合M={1,2,…,n}、边集合E={eij=(i,j)|i,j∈M}组成。节点之间的关系可用一个N×N的邻接矩阵A表示。用网络连接边的权重反映延误发生后城市间的高铁和航班连接情况,边权ωij表示为

(1)
网络构建的步骤如图1和图2所示。首先根据延误恢复计划和高铁时刻表,分别建立航空与高铁子网络。接着将同一城市的机场和高铁站点统一为一个节点,不考虑城市内部交通,从而将双层子网耦合为一张空铁联运拓扑网络。最后建立每条行程边的高铁时刻子表和航班时刻子表,储存两城市间的全部班次信息,将其改进为空铁联运时空拓扑网络。
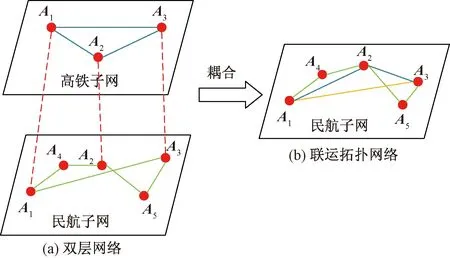
图1 空铁联运拓扑网络构建步骤Fig.1 Steps of air-rail combined transportation topology network construction
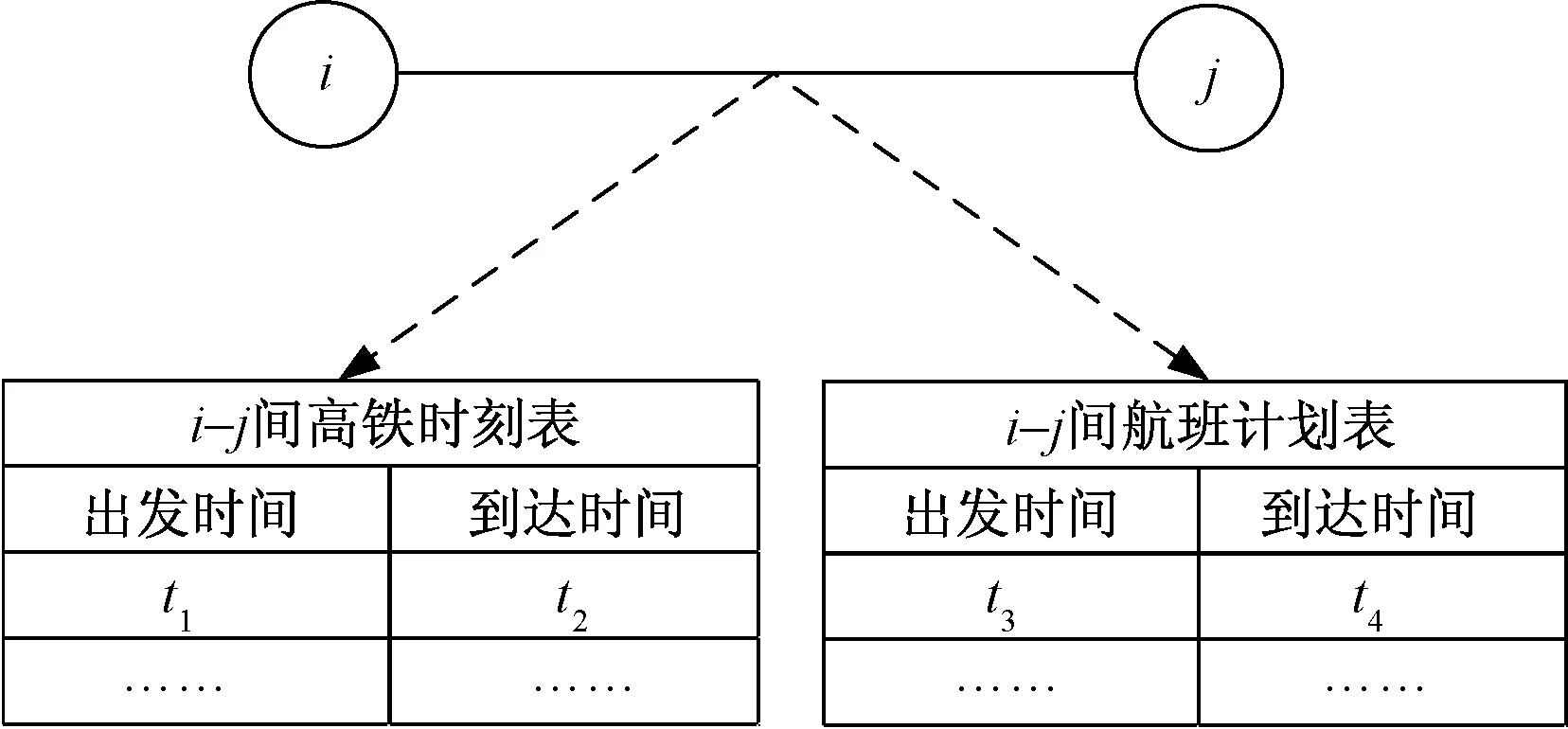
图2 赋予网络时间性Fig.2 Add time attributes to the network
2 旅客行程恢复模型构建
2.1 模型参数
在空铁联运时空拓扑网络的基础上建立旅客行程恢复模型。将相同行程起止点(OD)的旅客流统称为一个OD流。模型中涉及的主要参数在表1中列出。
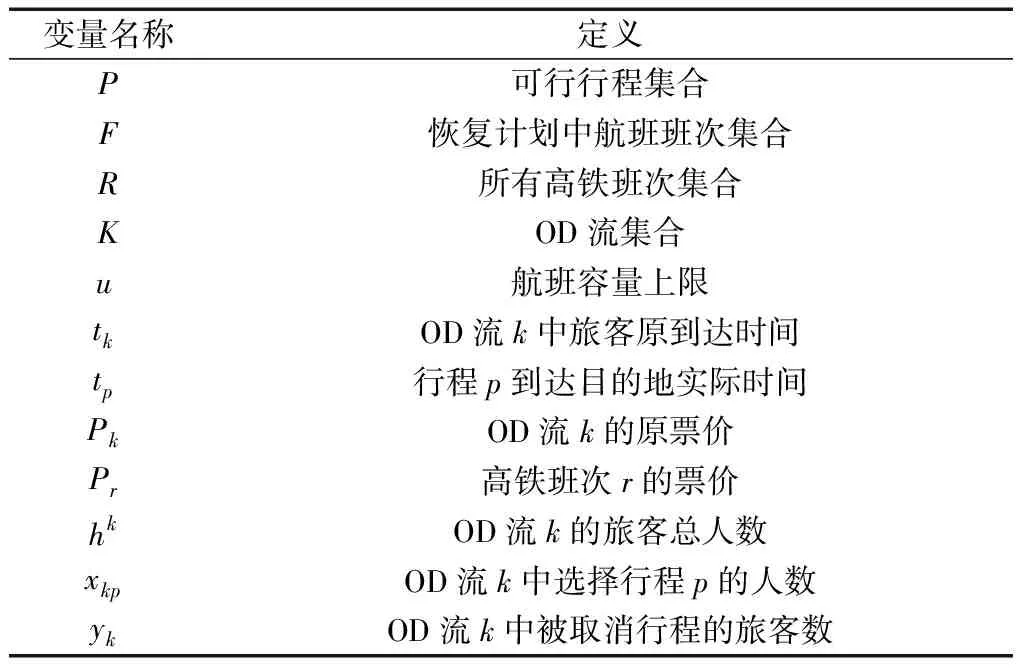
表1 旅客行程恢复模型基本参数Table 1 Basic parameters of passenger itinerary search algorithm
2.2 损失函数分解
构建旅客行程恢复模型的关键在于对延误损失的刻画。从航空公司角度出发,将延误恢复损失分为直接经济损失和旅客主观心理损失两部分。其中直接经济损失包括延误补偿损失、签转损失和取消损失;主观心理损失包括主观延误损失和主观取消损失。
参考Jiang等[12]运用前景理论研究旅客路径选择的方法,用效用损失来衡量旅客主观心理损失。前景理论中的价值函数为
(2)
式(2)中:v(Δx)表示旅客感知效用;Δx表示收益;λ为风险规避参数。
通常旅客对于延误的不满主要来自于长时间的延误等待,且原航班机票价格的高低可在一定程度上反映旅客对行程的重视程度。对价值函数进行转化,分别将两主观损失定义为与延误时长和原航班票价有关的函数。各损失的具体计算方法如下。
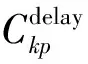
(3)
式(3)中:η为时间价值系数。参考文献[3],本文中将η设置为10.2。

(4)
式(4)中:λ为惩罚系数;Pr为高铁票价;当行程p中包括航班f时,σpf=1,反之,σpf=0。

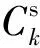
(5)
式(5)中:μ与θ为常量系数,在本文中的取值分别为2.25和0.69[12]。
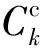
(6)
2.3 数学模型
F1为恢复过程中旅客总的主观心理损失,F2表示航空公司总的直接经济损失。根据第2.2节,可得
(7)
(8)
模型中以F1和F2之和为目标函数,即
F=F1+F2
(9)
对模型的求解旨在最小化F。考虑到实际运行中的各项规定,设置约束条件为
(10)
(11)
(12)
式(10)表示节点旅客流量平衡约束,即行程被取消和恢复的旅客人数之和为OD流总人数;式(11)表示旅客进行航班签转时须符合容量限制,即签转人数小于航班剩余座位数;式(12)为相关决策变量约束,两变量均为整数且非负。
2.4 旅客行程搜索算法
空铁联运时空网络中存在大量可行行程,为了高效搜索所有行程,设计旅客行程搜索算法。限制旅客在恢复行程中最多进行一次中转,考虑的恢复路径包括:原航班延误等待、签转至直达航班、签转至直达高铁以及乘高铁或航班至另一城市中转。
可行行程必须满足时间和空间衔接约束,即两段行程之间时间间隔满足换乘最短时间间隔的限制,且起讫地点为同一城市。规定航班签转最短衔接时间为40 min,空铁最短衔接时间暂定为45 min,按照航班行程优先的顺序从网络中搜索满足衔接条件的行程。算法思路如下。

旅客行程搜索算法流程Input: 受扰OD流集合K、恢复计划中所有航班集合F、高铁班次集合R、OD间空铁连接情况矩阵ΩOutput: 受扰OD流的可恢复行程Sfor k in K if ωij=0 (i,j表示受扰OD流k对应的两城市,ωij为矩阵Ω中的对应元素)在F和R中寻找满足衔接条件的中转航班或高铁,加入行程集合sk (sk∈S) else step 1:寻找满足条件的直达航班或高铁,加入行程集合sk step 2: 寻找满足衔接条件的中转航班或高铁,加入行程集合sk end ifend for
3 算例分析
3.1 情景设置
根据中国某航空公司实际航班样本数据,以及高铁部门官方网站发布的班期时刻信息模拟生成延误情景。实验过程基于如下假设:设置所有航班最大容量为100人,暂不考虑高铁容量限制;原计划航班客座率为80%;将延误时间超过30 min的旅客作为恢复对象;仅考虑延误时间小于300 min的恢复路径;惩罚系数λ取0.8(由航空公司文件给出)。
表2中给出了延误情景的基本情况,共涉及航班459个,旅客36 720名,机场12个。由于上海机场于某日10:00—15:00处于关闭状态导致大面积航班延误,对受干扰航班进行延误和取消等调整得到了航班恢复计划。

表2 延误情景基本参数Table 2 Basic Parameters of Delay Scenario
如图3所示,通过整理恢复期间高铁班期信息绘制空铁联运拓扑网络图。边粗细程度反应该时段下城市间的空铁连接情况。其中10个城市对间无高铁班次,8个城市对间无直达航班,1个城市对之间既二者均无,其余城市对间均同时具备高铁班次与直达航班。
3.2 实验结果及分析
导入时刻表信息,运用前述算法在拓扑网络中共搜索得到可行路径,可得路径总数为1 023,其中涉及签转高铁的行程数量为328。将可行行程代入模型进行求解,输出最优旅客恢复方案。
为验证考虑空铁联运恢复模型的有效性,将其与传统旅客行程恢复模型进行比较。传统恢复模型仅考虑取消航班、延误等待及改签至其他航班3种恢复方法。表3列出了传统模型和本文模型输出方案性能指标的对比情况。考虑空铁联运模型提供的可行行程数量约为传统模型的1.7倍,使得行程被取消的旅客人数显著减少(减少77%),且平均延误时间也有所降低(减少约10 min)。更多的旅客可以通过签转的方式对行程进行恢复,使得签转率由21.25%增至30.25%。说明考虑空铁联运的模型能够给予旅客更多的签转机会,从而为其提供更多恢复行程和缩短延误时间的可能性。
延误损失是航空公司最关心的指标之一,3种恢复方案的3种延误损失比较在图4中给出。可以看出与原恢复计划相比,传统方案和空铁联运方案均能同时减小3种延误损失,其中传统方案和空铁联运方案分别将原计划总损失降低了13.82%和23.87%。而本文模型输出的空铁联运方案在传统方案的基础上进一步减少了延误损失,使得主观心理损失和直接经济损失分别降低了15.46%和10.7%。

图3 延误情景下的空铁联运拓扑网络图Fig.3 Topological network diagram of air-rail intermodal transportation under delay scenario

表3 输出方案性能指标对比Table 3 Comparison of performance indicators of output schemes

图4 各方案延误损失对比Fig.4 Comparison of the delay loss of each plan
由于旅客行程取消带来的退票费用在经济损失中占比较大,故航空公司通常会避免退票的发生。而高铁的加入增加了城市之间衔接的途径,从而使大量原先被取消行程的旅客被重新安排,从而降低了由退票带来的巨额经济损失。同时,高铁带来的更多恢复方案给予不同需求的旅客更多样化的选择,确定的预计到达时间可以对旅客因航班时间不确定带来的消极情绪起到一定的缓解作用,从而降低了旅客主观心理损失。由此验证了考虑空铁联运恢复模型的有效性。
为了进一步探究影响空铁联运模式实施的关键因素,对空铁衔接时间限制进行灵敏度分析。将空铁最短衔接时间记作Δt,改变Δt的大小,分析输出方案的各项指标可得:
(1)通过表 4 不同衔接时间下的恢复情况可看出,衔接时间的增长使得大量空铁签转行程失效,限制了旅客可选恢复方案数量。当Δt由30 min逐步提升到60 min,签转率由31.75%减至27.75%,同时旅客平均延误时间由122.6 min增至138.7 min。取消旅客数量增长和平均延误时间的增大直接导致旅客主观损失增加7.6%,延误总损失增加4.4%。
(2)表5展示了4个典型航班的在不同衔接时间限制下的恢复方案,可以看出当Δt为30 min时,空铁联运方案占比较大,当Δt增至45 min和60 min时,空铁联运方案数量减少,航班签转方案数量增多。衔接时间限制增长后行程被取消的旅客开始出现无法被重新安排的情况,如F39航班的旅客在Δt为60 min时只能取消行程;延误航班的旅客只能等待原航班,如F98航班的旅客在Δt为30 min时可通过空铁联运缩减延误时间,当Δt为45 min时只能选择原航班延误等待。
由此可见,衔接时间限制很大程度上影响了考虑空铁联运恢复方法的实施效果。在实际运行中,空铁站点间的摆渡及手续办理正是限制联运方法普及的瓶颈所在。因此,航空公司应该通过加强与高铁部门的合作,实现更为高效便捷的空铁联运。

表4 不同衔接时间下的恢复情况Table 4 Recovery under different connection times
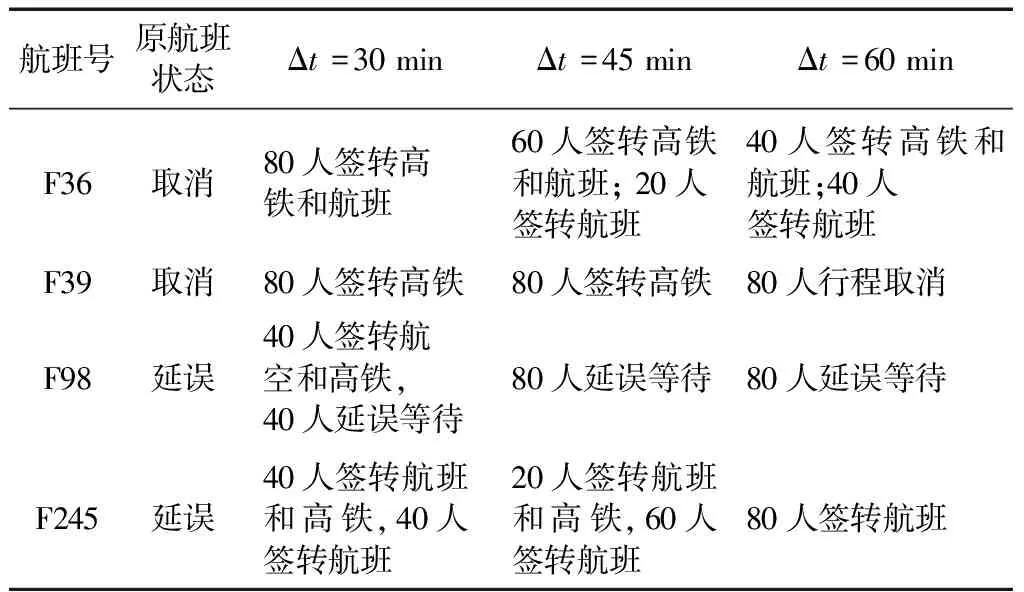
表5 典型航班不同衔接时间下的恢复方案Table 5 Recovery plan under different connection times of typical flights
4 结论
以延误旅客行程恢复问题现有研究为基础,通过构建空铁联运时空拓扑网络建立旅客行程恢复模型。提出的恢复方法相较于传统延误处置方法,为旅客提供了更多样化的恢复方案。本文的主要研究工作如下。
(1)将航线网络与高铁网络耦合,在空铁拓扑网络结构的基础上,依据具体延误情景下的班期时刻信息,构建空铁联运时空拓扑网络。利用网络实现对可行行程时间和空间两个维度的描述。
(2)同时考虑直接经济损失和旅客主观心理损失,建立以恢复总损失最小为目标的旅客行程恢复模型。设计旅客行程搜索算法,在时空拓扑网络中高效搜索可行行程并记录行程延误时间等信息。
(3)模拟延误情境,对比模型输出方案传统恢复方案的各项恢复性能。结果表明,考虑空铁联运的方案能兼顾航空公司与旅客双方利益,减少航班延误带来的损失。灵敏度分析表明,空铁换乘的衔接时间限制时影响空铁联运方案实施的关键环节。
