考虑脆弱性的离散交通网络设计

2022-11-04庞远兵张玺石超峰

科学技术与工程 2022年27期

庞远兵，张玺*，石超峰

(1.重庆交通大学交通运输学院，重庆 400074； 2.重庆交通大学经济与管理学院，重庆 400074)

随着交通需求的日益增长，道路交通网络在运行中需要面对越来越多的不确定性，如自然灾害、交通事故、道路施工、蓄意袭击等，某些脆弱路段或节点受到不确定事件的冲击很有可能导致整个交通网络的运行效率大幅度下降，引发关联路段级联失效，甚至崩溃。因此，准确地识别交通网络中的脆弱单位，有效降低其脆弱性以保证交通网络的稳定运行，具有非常重要的现实意义。

目前关于脆弱性概念的基本思想均强调事件攻击对路网造成的损失后果，即指受到交通灾害引起路网交通功能降低的敏感性,道路单元失效所带来的后果越严重表明道路网络越脆弱。国内外学者从多个方面探讨了交通网络的脆弱性评价方法，如可达性[1]、连通性[2]、鲁棒性[3-4]、网络拓扑结构[5]、网络效率[5-7]等，其中基于网络效率的评价指标应用较为广泛。文献[8]将网络效率定义为所有节点对间最短距离倒数的平均值，在此基础上，Yin等[5]采用路段失效前后网络效率的变化率作为脆弱性评价指标，并通过优化路网结构来降低路网脆弱性。叶青[9]利用节点失效前后网络效率的变化差值来评价节点脆弱性，并以重庆市轨道交通网络为例，定量计算各个站点对于蓄意攻击的脆弱性，以鉴定对网络效率影响最大的关键站点。Chen等[10]在研究城市群内交通网络的脆弱性和恢复性时，将路网单元失效前后的网络效率之比作为脆弱性评价指标，并利用交通网络的弹性来描述路网在攻击下的恢复能力。但他们都仅考虑了道路网络的结构问题，而没有考虑到路网中的动态流量问题。Husdal[11]对路网脆弱性的影响因素进行分析时发现，影响道路交通网络脆弱性的网络性质不仅包含结构属性，还包括交通量属性。因此基于文献[8]建立的脆弱性评价指标的缺陷在于无法反映交通量对脆弱性的重要影响。

目前对道路交通网络脆弱性的研究大多停留在理论层面，对于如何将脆弱性指标和脆弱性分析融入整个路网规划设计中的研究鲜见报端。作者认为在脆弱性识别后，可以通过优化路网结构、扩建当前道路、控制交通量和合理分流等方法来降低路网脆弱性。文献[1]采用扩展当前道路的方法降低路网脆弱性，但扩建道路在建设时期会对交通状况造成极大影响；文献[5]提出增加连接和重新布线两种方法来优化路网结构脆弱性，降低对路网正常运输功能有重大影响的关键路段的脆弱性，但在优化过程中没有考虑路网中的流量问题。

基于以上分析，在改进基于文献[8]的脆弱性评价指标的基础上，并不考虑路段失效概率的情况下，采用路段轮流断裂失效的方法，利用静态交通均衡分配结果评价各路段断裂对路网服务效率下降程度的影响，以此来识别路网中的脆弱路段。针对路网的脆弱状况，通过增加连接的方式降低路网脆弱性，并构建一个以路网脆弱度最小化为目标函数的上层规划模型，用户均衡为下层模型的双层规划模型来对路网进行优化设计，以在有限的资金条件下最大程度降低路网整体脆弱性。

1 脆弱性评价指标

1.1 基于网络效率的脆弱性指标

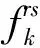
使用BPR(bereau of public roads)函数计算各条路段的出行成本，其计算公式为

(1)

Latoral等[8]基于无向加权网络提出了小世界网络效率的评价模型，将网络效率定义为所有节点对间最短距离倒数的平均值，现采用节点之间的出行成本代替最短距离，可将改进后的网络效率定义为

(2)

根据式(2)这种网络效率评价方法可将路段的脆弱性定义为

(3)

式(3)中：V(a)表示路段a的脆弱度，V(a)的值越大表明路段a越脆弱；E表示道路网络结构完好时的网络效率；Ea表示当道路网络中路段a被移除后的网络效率。

将路网的整体脆弱度定义为路网中所有路段脆弱度的平均值，可表达为

(4)

式(4)中：V为路网的整体脆弱度，简称“路网脆弱度”，路网脆弱度V越大表明路网整体越脆弱。

1.2 脆弱性指标的合理性分析

采用仅有2个节点的简单网络为例，对基于网络效率的脆弱性指标进行合理性分析。如图1所示，路网中仅有2个节点，2个节点间有n(n≥2)条路径连通，每条路段的通行能力均为c，OD对(1，2)之间的OD需求为q。假设图1路网中所有路径上的出行成本函数相同，均采用如式(1)所示的BPR函数形式。

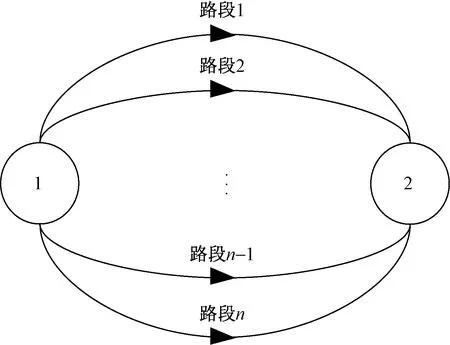
图1 简单网络Fig.1 Simple network

根据式(2)可得此时路网网络效率为

(5)

由于所有路段的出行成本函数相同，因此在达到均衡时的路网中，每条路段上的交通流量必定相等且均为x=q/n，当路网中任一路段a被截断失效后，路网中每条路段上的交通流量为x=q/(n-1)；并且此时路网脆弱度V和任一路段a的脆弱度V(a)相等，结合式(3)可得

(6)

由于参数α、β、q、c均大于0，且n≥2，由此可以确定路网和任一路段a的脆弱度值的变化范围为：0≤V≤1、0≤V(a)≤1，当某路网中有且仅有1条路段时，路段脆弱度V(a)取1，当某路网中路段a没有承担交通流量时，路段脆弱度V(a)取0。

针对式(6)用路网脆弱度V对路段数量n求偏导可得

(7)

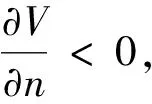
针对式(6)用路网脆弱度V对交通需求q求偏导可得

(8)

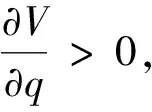
综上，证明基于式(4)的道路交通网络脆弱性指标能够全方位地反映路网中的网络结构、交通需求、出行选择和出行成本等因素对路网脆弱性的影响，不仅能考虑路网的连通性，而且还兼顾了路网的流量特征和空间拓扑特征，将式(4)作为道路交通网络脆弱性指标具有合理性，基于这种道路交通网络脆弱性指标展开对交通网络的优化设计研究。

2 双层规划模型的建立

一般道路交通网络设计问题(network design problem,NDP)是指在一定的投资约束条件下，考虑交通出行者行为选择的同时，为达到某种系统指标最优，对部分路段进行改进或在交通网络中增加新路段的最优投资决策问题。由于NDP决策过程涉及政府部门与公众之间的互动，是一个典型的双层决策问题，因此双层规划则成为描述交通网络设计问题的理想工具。本文中也采用双层规划模型来描述考虑路网脆弱性的交通网络优化设计问题，其中上层模型是以路网脆弱度最小化为目标的优化模型，下层模型为用户均衡配流模型。

上层规划模型为

(9)

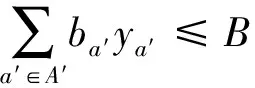
(10)

ya′∈{0,1},a′∈A′

(11)

用户均衡配流模型作为双层规划的下层模型，模型建立为

(12)

(13)

(14)

(15)

式中：路网中的待建路段集合为A′，待建路段a′∈A′;待建路段a′的建设费用为ba′，总建设资金上限为B;式(9)中的路段集合A不仅包含了原路网中的路段，还包含新建路段；ya′为决策变量，定义为

(16)

在上层规划模型中，式(9)是以路网脆弱度最小化的目标函数，式(10)为资金约束，式(11)为变量取值约束。下层规划模型中各式具体含义可参见文献[12]。

3 算法设计

由于离散网络设计问题(discrete network design problem,DNDP)的复杂性和非凸性，经典算法很难求解,常采用启发式算法[13]。其中遗传算法(genetic algorithm,GA)的计算复杂度相对较优，设计GA算法求解上层规划模型，并结合Frank-Wolfe算法求解下层用户均衡配流模型,设计求解算法步骤如下：

Step1编码。采用二进制编码形式，将原问题的解映射到染色体上，如若路网中有7条待建路段，那就用染色体长度为7的0-1变量表示一个染色体，一个染色体编码代表一种建设方案，如[1001011]，1表示对路段1、4、6、7进行建设，0表示不建设路段2、3、5。

Step2生成初始种群。设定GA算法的种群规模为psize，交叉概率为pc，变异概率为pm，最大进化代数为Gmax，随机生成具有psize个个体的初始种群。

Step3个体对应的目标函数值计算。调用Frank-Wolfe算法配流后可计算得到原网络效率E，用种群中每个个体分别更新路网，轮流断开路网中的路段，可得到每条路段失效后的网络效率Ea，从而得出每条路段的脆弱度V(a)，最终利用式(4)计算得到每个个体对应的路网脆弱度V(V>0)。

Step4适应度值计算。将适应度函数定义为f=1 000 000/V，适应度值越大，个体被选择的概率越大。

Step5约束处理。通过设计罚函数将约束问题转化为无约束问题，设计个体i对应的罚函数为

(17)

重新定义适应度值为

Fi=fimi

(18)

Step6选择策略。直接选择一个最优个体遗传到下一代，本文按照轮盘赌法选择其余个体，基于适应度比例的选择策略，个体i被选择的概率为

(19)

式(19)中：N为种群大小。

Step7交叉操作。根据交叉概率pc，采用单点交叉的方式随机选择交叉位置进行交叉操作。

Step8变异操作。根据变异概率pm，使得子代种群中每个染色体的基因都根据变异概率进行变异，得到新种群。

Step9算法终止。如果迭代次数G>Gmax，算法终止，输出最优个体及对应的目标函数值，否则转入步骤3。

由于篇幅所限，利用Frank-Wolfe算法求解用户均衡模型的详细步骤不再叙述，可参见文献[12]。

4 算例分析

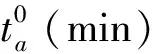
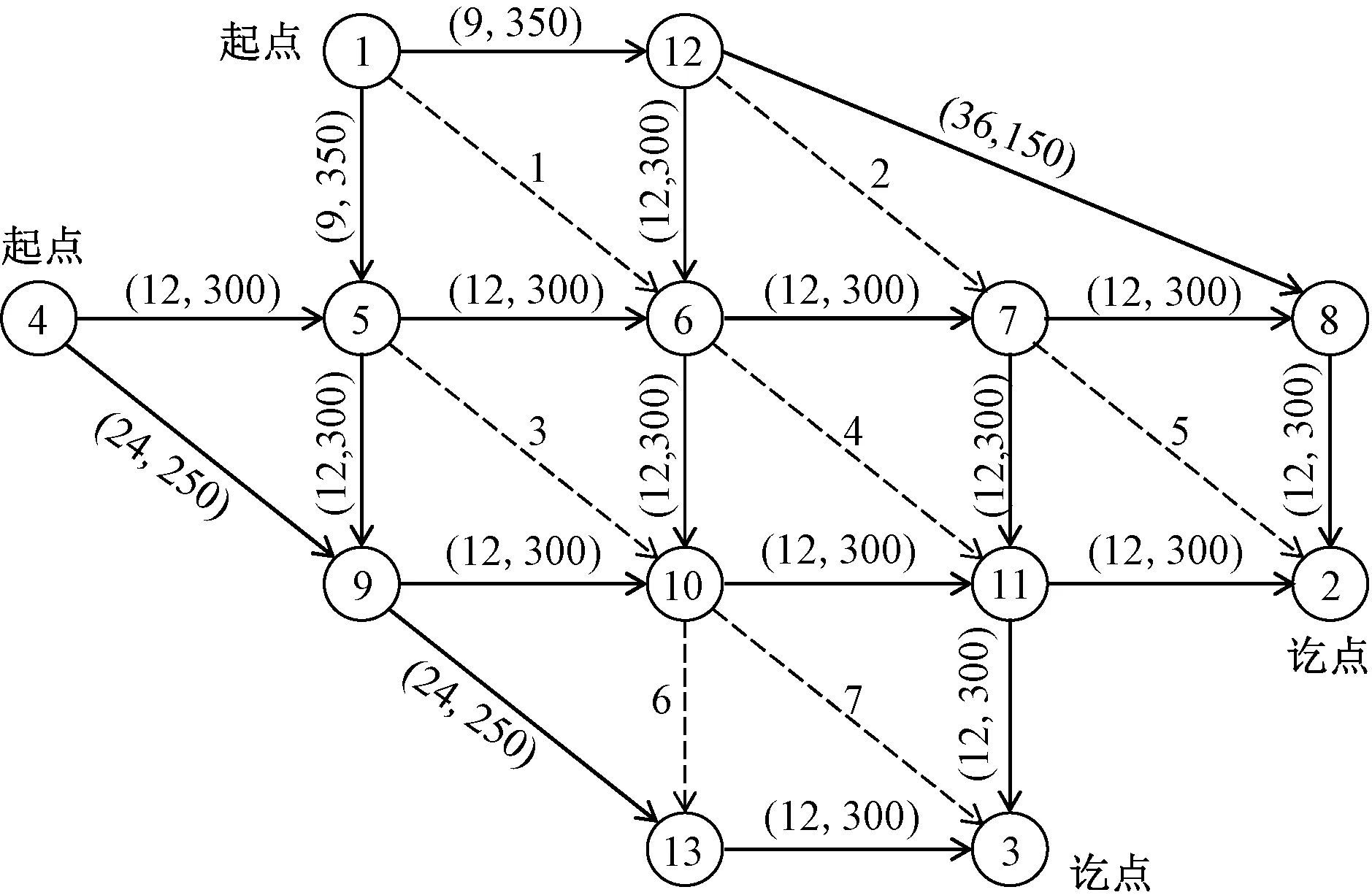
图2 算例网络Fig.2 Example network

表1 待建路段相关参数Table 1 Relevant parameters of sections to be built

为了分析费用对最优建设方案的影响规律，将建设资金约束B从初始100万元逐次提升至700万元，得到在目标函数下的优化结果如表2所示(只展示脆弱度排名前7的路段脆弱度变化情况)，并将本文这种优化方案设置为方案1。

文献[5]中作者在研究路网的结构脆弱性时发现，将新建路段按照就近原则优先建设在脆弱度最高的路段附近，可以更好地降低脆弱路段的脆弱性，当考虑流量时还可以起到为脆弱路段分担流量的作用。所以可以按照既有路段脆弱度大小确定待建路段的优先级，如在本算例中既有路段脆弱度从高到低排序为路段1-12、9-13、13-3、10-11、6-7、8-2、5-6，则待建路段的优先级按照就近原则可确定为路段1、6、7、4、2、5、3，并将这种建设方案设置为方案2，优化结果如表3所示。

4.1 方案对比

从表2可以看出，方案1中待建路段的优先级并不是固定的，这和方案2的优化逻辑有所不同。由表2、表3的优化结果对比可以发现，方案1和方案2都可以一定程度地优化脆弱路段，相对而言方案2对于个别脆弱度高的路段优化效果更好，但从所有路段来看，如图3所示，在同等建设资金条件下,方案1可将更多的路段脆弱度降低到理想值，例如建设资金约束为200万元时，方案1有11条路段脆弱度降低到理想值，方案2只有7条路段达到理想值；建设资金约束为300万元时，方案1中脆弱度达到理想值的路段有13条，而方案2中只有仅仅7条。说明在对所有路段的优化效果上看，方案1明显更具有优势。

如图4所示，在同等建设资金约束下，方案1优化后的路网脆弱度更低。如在建设资金约束为200万元时，方案1的路网脆弱度比方案2多降低10.6%；在建设资金约束为300万元时，方案1比方案2多降低9.1%；建设资金约束为400万元时，方案1比方案2多降低7.5%。无论在700万元以下的何种资金条件下，方案1在对路网脆弱度的优化效果上明显优于方案2。

表2 方案1的优化结果Table 2 Optimization result of scheme 1

表3 方案2的优化结果Table 3 Optimization result of scheme 2

图3 路段优化情况对比Fig.3 Comparison of road section optimization

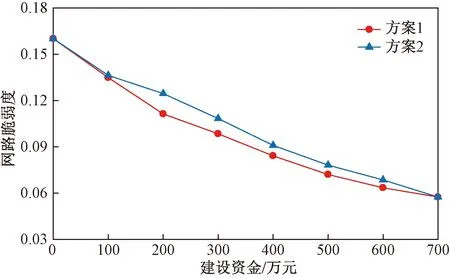
图4 路网脆弱度优化结果对比Fig.4 Comparison of optimization results of road network vulnerability

当建设资金约束为300万元时，方案1和方案2同样都新建了路段1，方案1将路段1-12的脆弱度从0.270 6下降到0.137 5，而方案2只将路段1-12的脆弱度下降到了0.147 3，说明专门针对脆弱路段设计的方案2并不一定就比方案1有效，这是因为在交通网络中各个组成部分之间会相互影响，是一个复杂的系统性问题，从单一点入手根本无法保证有效解决这种问题。方案1 以系统整体的角度出发，将路网脆弱度最小化作为优化目标，相比于方案2更具系统性和全面性。

4.2 不同OD需求下的建设资金选择

在方案1中，既有路段的脆弱度变化情况如图5所示，可以看出在原始路网中路段的脆弱度普遍较高，随着建设资金的提升，各条路段的脆弱度逐渐下降，但可以发现建设资金达到300万元以上时，随着建设资金的提升各路段的脆弱度变化情况并不明显，主要徘徊在0.09上下，说明固定OD需求下，应选择合适的建设资金投入，避免造成资源浪费。

图5 不同建设资金约束下的路段脆弱度Fig.5 Section vulnerability under different construction fund constraints

图6 不同OD需求下的路网脆弱度优化情况Fig.6 Optimization of road network vulnerability under different OD requirements

为尽量保证资金投入后的效益，设置投入的建设资金使路网脆弱度下降到理想值即可。图6为不同OD需求下，路网脆弱度的优化情况。可以看出，随着建设资金的提升，路网脆弱度的优化效果逐渐变弱，并且在同一资金约束条件下，OD需求越大，路网脆弱度也越大。可以发现，在OD需求为600 pcu/h时，只需投资200万元即可使路网脆弱度达到理想值，此时路网脆弱度下降32.9%；OD需求为800 pcu/h时，需投资300万元，此时路网脆弱度下降38.5%；OD需求为1 000 pcu/h时，建设资金需要达到500万元才能使路网脆弱度降低到理想值，此时路网脆弱度下降44.8%，3种OD需求下的优化效果都相当显著。

图7为不同OD需求、不同建设资金约束条件下的优化结果，路网脆弱度0.1处设置了一个脆弱度理想值平面。从OD需求维度看，随着OD需求的增长，路网脆弱度逐渐升高，并且需要投入更多的建设资金才能使路网脆弱度降低到理想值。从建设资金维度看，随着建设资金的增加，路网脆弱度逐渐降低，但降低的程度逐渐变弱。而且可以看到在OD需求较小，建设资金较大时，路网脆弱度的优化效果甚微，因此在优化过程中应根据实际的交通需求，选择合适的资金投入，避免造成资源浪费。