混沌图像加密算法安全性能研究
2022-11-04陈树彬
陈树彬
(韩山师范学院,广东 潮州 521000)
hssycsb@vip.163.com
1 引言(Introduction)
图像是信息交流的重要载体,大数据时代中图像的产生数量呈几何倍增长,图像的使用范围越来越广,而日益多发的网络安全事件引发了学者对图像传输安全的关注,这使得对海量图像进行加密的重要性日益凸显。作为20 世纪的重要发现之一,混沌系统由于其自身的不确定性、伪随机性以及对初始加密参数的敏感性等特点,具备了应用于图像加密的天然条件。1979 年,FRIDRICH第一次将混沌系统应用到了图像加密中,由此开启了混沌加密在图像加密领域的研究。CHEN等在二维混沌Cat映射的基础上将之推广到三维,形成了一个基于对称图像的加密方案,该算法是先以Cat映射对原图像像素进行置乱,再将明文图像与密文图像之间的关系进行打乱。HUA等则是用两层混沌映射产生混沌序列来设计图像加密算法,取得更为理想的加密效果。之后PAK利用Logistic、Sine和Chebyshev映射,先是对明文图像利用混沌生成序列进行置乱,再进行扩散操作,并将得到的密文循环左移。
针对各种混沌加密算法在图像加密领域的应用,其算法的安全性、鲁棒性等性能的好坏是衡量算法可行性的重要特征,下面将给出几个定量对图像加密系统的安全性能进行分析和测试的指标。
2 衡量混沌图像加密算法安全性能的主要指标(The main indicators to measure the security performance of chaotic image encryption algorithm)
混沌加密在图像加密上的应用能够使得在获取加密图像后,直接感受为毫无意义的伪随机图像,且通过任何手段均提取不到任何有关明文的信息;攻击者利用各种密码分析方法均仍难以得到任何有效的信息。混沌系统加解密图像流程图如图1所示,混沌图像加密方法通常将混沌系统作为伪随机序列发生器,生成的伪随机序列作为密钥序列与明文进行加密运算从而得到随机的密文。研究表明,借助混沌系统产生密钥序列在安全性和简便性等方面都有较好的表现。
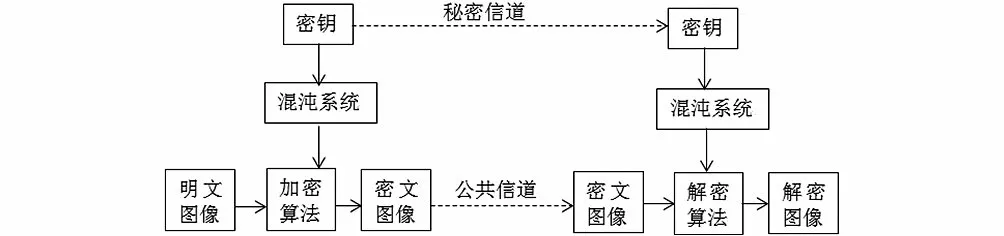
图1 混沌系统加解密图像流程图Fig.1 Flow chart of chaotic system encryption and decryption image
对混沌图像加密算法的安全性以及鲁棒性等方面进行综合评价,是考查一个加密算法是否适应于实际应用的重要过程。因此,算法评价也是一个重要的研究内容,以下将分别就算法各方面性能定量指标进行详细说明。
2.1 加密图像直方图比较及其信息熵计算
图像是安全性分析的一个重要工具,其横坐标表示样本数据,纵坐标是相应样本出现的个数,通过加密的图像直方图若呈现较为均衡的状态,则说明其对原始图像的像素关联置乱效果较好,也能对统计攻击进行抵御。衡量混沌加密算法的好坏可以对加密前后的图像直方图进行对比,要使加密后的图像未保留明文的任何信息,则其直方图应呈均匀分布,说明该算法是一个较好的加密算法,因为很难从密文中得到明文的相关信息,从而实现了理想的加密效果。为了更加科学客观地反映加密图像的直方图是否均匀分布,我们引入如式(1)的加密图像信息熵来定量表示:

这个熵值的最佳理论值为8。
2.2 图像变化度
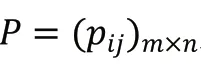

2.3 平均互信息分析

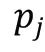
2.4 密钥敏感性
加密的过程,其实也是密钥生成的过程。差分攻击是一种常见的攻击手段,攻击者通过对获取的明文图像差别来获取密钥。如果密钥信息的微小改动,能引起加密信息的巨大变化,则说明此加密算法对密钥极为敏感,我们称其为加密算法的密钥敏感性,那此算法就能应对差分攻击。我们将通过对密钥的细小改动,再用改动后的密钥去解密改动前加密的密文,从解密的效果上去衡量加密算法对密钥的敏感性,敏感性越强,则说明算法安全性越高。
3 Logisitc混沌系统图像加密算法安全性能测试(Security performance test of image encryption algorithm in Logisitc chaotic system)
Logistic映射又被称为虫口映射,是混沌映射中一种较为常用的映射算法,利用其对初值的敏感性可生成数量多、相关性小、类随机的混沌序列。Logistic映射对初始值极为敏感,其规律性、遍历性和复杂的不可预测行为,使得它在信息加密领域被广泛关注。同时,Logistic混沌映射在空气动力系统和混沌等复杂系统上的研究也被广泛关注。下面我们将以混沌图像加密算法中的Logisitc映射加密算法为例,针对上面的四个指标分别测试其算法性能。Logistic混沌系统由式(8)给出:

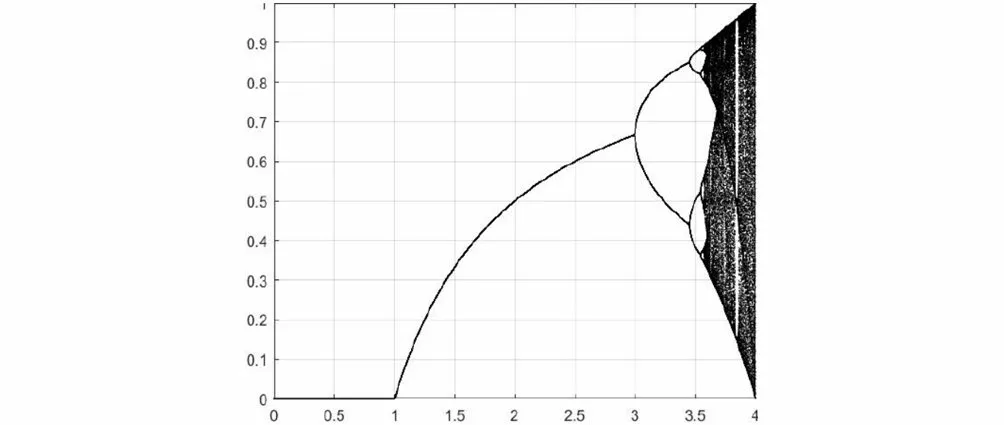
图2 Logistic映射图Fig.2 Logistic mapping
Logistic映射的混沌加密、解密设计流程如图3所示,其通过Logistic迭代的方式得到一组随机序列,再利用这个序列生成密钥,用于对图像进行加密。下面是对流程的简单描述:
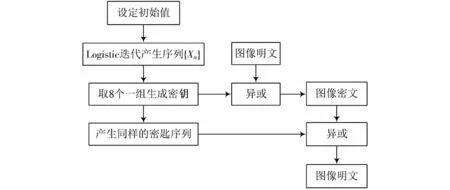
图3 Logistic映射的混沌加密、解密流程Fig.3 Chaotic encryption and decryption process of logistic mapping
(1)先是给定一个适当的初始值,利用Logistic映射方程,经过数次迭代后得出一个随机序列;
(2)利用生成的随机序列形成密钥信息序列,与需要加密的明文信息(原图像)序列进行异或运算,得到密文信息(加密图像)序列;
(3)以上面相同的密钥信息序列,将其与密文信息序列一起来做异或运算,就解密出图像的明文。
下面我们以一幅256×256的图像test.gif(图4)为例,以MATLAB作为开发平台,对图像进行加密,得出加密图像(图5)并逐个指标对照测试。

图4 原图像Fig.4 Original image

图5 加密图像Fig.5 Encrypted image
3.1 加密前后直方图对比
针对测试图像加密前后的直方图分别如图6和图7所示。
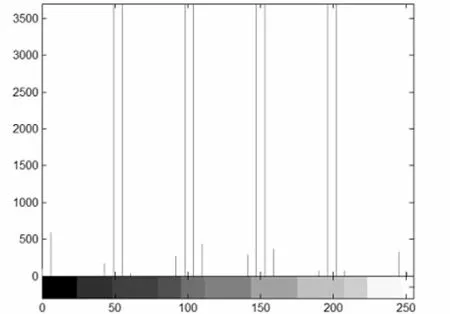
图6 原图像直方图Fig.6 Histogram of original image
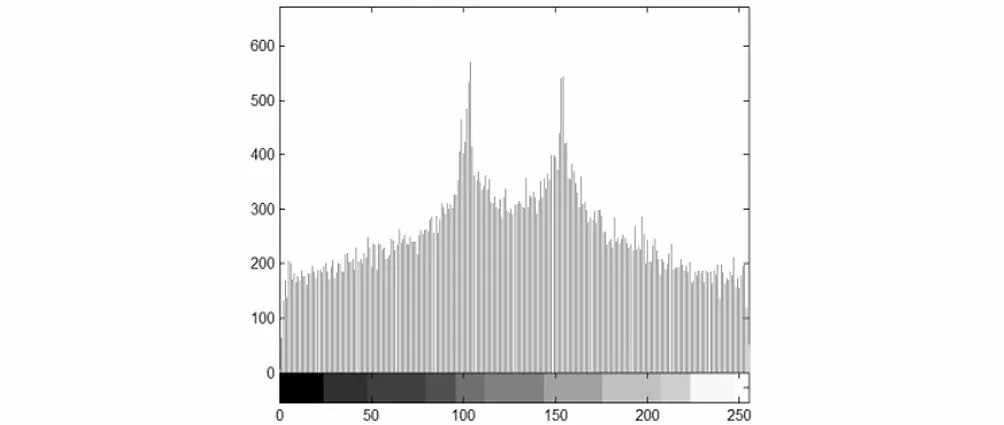
图7 加密图像直方图Fig.7 Histogram of encrypted image
根据式(1)计算出加密后的图像直方图信息熵得出:
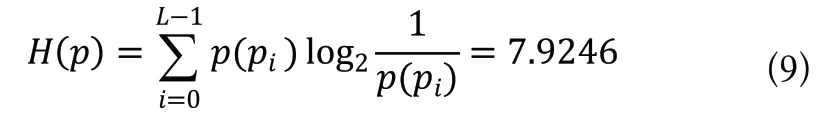
我们可以看到计算出来的信息熵非常接近理论值8,说明加密后的图像直方图呈现均匀状态,因此攻击者很难从密文中获得明文的任何信息。
3.2 图像变化度的计算
根据式(3),我们可以计算出
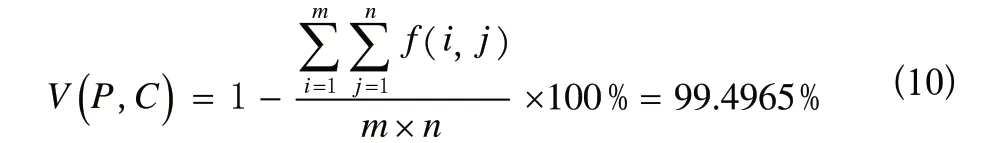
从这个值我们可以看出混沌加密算法对图像的置乱效果非常好。攻击者几乎无法从加密信息中获取任何信源信息。
3.3 加密后的图像平均互信息计算
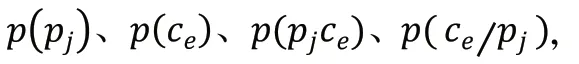
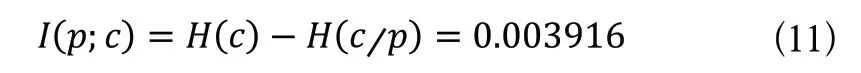
通过平均互信息这个参量我们可以从信息学的角度量化出能够从密文得出明文的信息量。这个值说明图像加密效果较好,密文中关于明文的信息已所剩无几。
3.4 密钥敏感性测试
为了测试加密算法对密钥的敏感性,我们对密钥进行细微的调整,分别用密钥K1(0.1,0.2)和K2(0.1000001,0.2)进行加密得出加密图像C1(图8)和C2(图9),再分别用K2对C1进行解密,用K1对C2进行解密,得到图10和图11。

图8 加密图像C1Fig.8 Encrypted image C1

图9 加密图像C2Fig.9 Encrypted image C2

图10 K2对C1解密图Fig.10 Decryption diagram of K2 for C1

图11 K1对C2解密图Fig.11 Decryption diagram of K1 for C2
实验结果表明此混沌图像加密算法对密钥是非常敏感的,两个密钥即使只有细微的差别,也不能相应地对对方的加密图像进行解密,可以看到互相解密效果非常差,明文图像的任何信息几近无法得出。说明这个混沌加密算法对密钥具有非常强的敏感性。
4 结论(Conclusion)
本文首先对相关混沌图像加密算法的发展进程进行综述,然后提出了衡量加密算法安全性及鲁棒性等特征的四个定量指标,分别为加密前后图像直方图比较、信息熵计算、图像变化度、平均互信息分析及密钥敏感性等,用以对算法性能进行综合比较分析,并通过Logisitc映射生成一组伪随机序列生成密钥,再使用这个密钥对相关实验图像进行混沌加密,使用MATLAB软件作为实验工具,对加密图像算法以四个加密算法安全性能衡量的指标进行分析。结果表明,加密前后的直方图计算出来的信息熵相当接近理想值,图像的变化度也较大,平均互信息值较小且密钥敏感性较高,说明相关图像加密算法具有很好的安全性和鲁棒性,也能够应对各种攻击手段的攻击。
