对牵连速度两种观点的辨析与思考

戎 杰

（浙江省慈溪中学，浙江宁波 315300）

“微元法”和“等效法”是分析、解决物理问题的常用方法.在牵连问题中，一个物体带动另一个物体运动，在确定彼此速度的定量关系时，通常会涉及到运动的分解.如果学生形成盲目、死板记忆“沿绳方向和垂直绳方向分解速度”的结论，容易形成思维惯性，不利于科学思维的形成和核心素养的培育.从物理教学的有效性和学科素养培养的角度来看，要使学生对物理规律“知其然而知其所以然”.笔者尝试用“微元法”“等效法”“图像法”“复合函数求导法”等方法，对一个牵连速度问题的两种观点进行辨析与思考.

问题：如图1，水平面上有一辆拖车P，高为h的水平高台上有一辆小车Q，两车之间用不可伸长的绳跨过定滑轮连接，当P 车在水平面上以速度v匀速行驶时，高台上的Q 车速度如何变化？加速度如何变化？

图1

在教学中，笔者发现学生思维中存在两种观点.

（1）Q 车速度判断：根据P车在向右运动过程中，有使滑轮右侧绳子伸长并绕滑轮做圆周运动的“实际运动效果”，所以可把P 车的水平速度v进行分解，如图2，沿绳方向的分速度v1=vcosθ，垂直于绳方向的分速度v2=vsinθ，Q 车的速度vQ等于P 车沿绳方向分速度v1.随着P 车向右运动，θ减小，cosθ增大，因此Q 车向右做加速运动.

图2

（2）Q 车加速度判断：做出Q 车的速度 时间图像.由于加速度是速度的变化率，对速度函数求导，加速度大小｜a｜=｜v1′｜=vsinθ.由图3可知，随着θ不断减小，sinθ不断减小，加速度a不断减小，因此Q 车做加速度不断减小的加速运动.

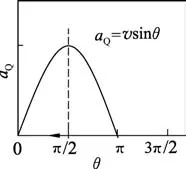
图3

上述两种观点是否正确？

对于观点（1），不少学生对于P 车的“实际运动效果”普遍不甚理解.P车明明水平向右运动，怎么会有绕滑轮做圆周运动的效果呢？笔者认为，可尝试用“微元法”论证上述速度分解方法的正确性，解决学生心中的困惑.

如图4，设P车在Δt时间内从A点运动到了B点，若取Δt→0，则绳OA、OC间夹角Δθ→0，即∠OAE=∠OBE=θ.

图4

在OB上取C点，使｜OA｜=｜OC｜，因Δθ→0，∠OAC=∠OCA=90°.Q 车向右运动的距离，即绳子伸长的距离.xQ=｜OB｜-｜OA｜=｜OB｜-｜OC｜=｜CB｜.

而｜CB｜=｜AB｜cosθ=v·Δtcosθ.

有vQ==vcosθ=v1.随着θ的减小，cosθ增大，Q 车速度增大.

由“微元法”分析结果可知，把P 车的速度v沿绳和垂直于绳方向进行分解是正确的.

对于观点2，加速度是速度关于时间的变化率，而观点2中求得的Q 车速度vcosθ.是v关于θ的函数.若对速度函数直接求导得到的是v关于θ的导函数，而不是v关于t的导函数，所以并不表示加速度，因此通过v θ函数图像的斜率判断加速度的方法是错误的.

进一步分析，若设P车从E点出发经过时间t运动至A点，有如下3 种方法可判断Q 车的加速度.

方法1：速度函数图像法.

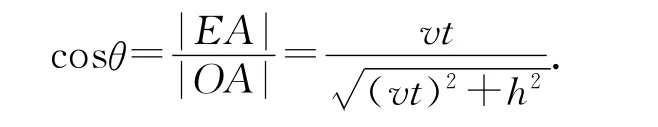
图5

方法2：复合函数求导法.

由结果可知，随着t的增大，a不断减小，Q 车做加速度减小的加速运动.

方法3：等效法.

图6

根据P 车水平面上做匀速直线运动，所以加速度为0.现在“无中生有”，将“零”等效为a1、a2、an、aτ4 个分加速度：a1=an，a2=aτ.由P 车绕O点做圆周运动的分运动来看，在t时刻，P车有指向O点的向心加速度an，和使绳子变长的加速度a1等大反向，即Q 车的加速度.

综上，对一道关联速度问题的两种观点进行辨析与思考，体会微元法、图像法、复合函数求导法、等效法等方法在分析、解决高中物理问题中的重要作用，由浅入深、由易至难，前三种方法旨在体现运用数学方法解决物理问题的“数理结合”关键能力，等效法侧重体现物理学科思想方法，提升物理思维品质，体会物理学科精神.