基于视觉的自主无人机目标跟踪着陆方法研究

孙 凯，于 洋，冯迎宾

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)

近年来，因具有体积小，隐蔽性强等优点，无人机被广泛应用在军事和民用领域，如空中侦察、火力引导、搜索救援、地图绘制等。机械结构简单且对起降环境要求低的多旋翼无人机成为本领域的研究热点。随着无人机在各行业应用不断加深，用户对无人机提出了新的功能需求，如移动目标的有效识别、动态跟踪能力以及可靠的抗干扰能力等，对多旋翼无人机的跟踪着陆和飞行姿态控制技术提出了更多挑战。

无人机自主着陆技术[1]的出现大大提高了无人机的自主性并有效地解决了手动操控方式带来的问题。无人机自主着陆涉及机体在空间中的定位，着陆平台的识别、跟踪以及飞行控制等方面。地面站处理数据[2]和机载电脑处理数据是无人机自主着陆技术的两个研究方向。地面站处理需要通过地面站与无人机建立通信，并经由无线数据传输设备接收无人机回传的各项数据信息，地面站再将控制信息发送回无人机。这种方式可以同时处理更多的数据，但整个过程存在较大的时延和失真，难以满足四旋翼无人机自主降落需求。机载处理方式由于配备了机载处理器，可实时处理数据并运行控制程序，保证了四旋翼无人机定位的实时性和精确性。嵌入式计算机性能的大幅度提高使得机载处理方式成为主流的研究方向。

全球卫星定位系统(GPS)[3]和惯性导航系统(Inertial Navigation System，INS)常用于无人机在外部环境的定位，但仅依靠GPS和INS引导无人机进行自主跟踪着陆会有一定的不足。首先，INS的特性会导致其定位误差随时间增大，影响无人机安全飞行；其次，一般商用GPS米级的定位精度很难满足无人机自主着陆的需求，在某些特殊应用环境，如建筑物之间、大型建筑物的内部等，微弱的GPS信号导致定位误差超过安全阈值，无人机很可能会出现坠毁的情况，而高精度的GPS差分定位系统[4]的质量、体积均较大且价格昂贵，难以安装在无人机上。

鉴于GPS使用范畴的局限性，无人机大多采用视觉辅助定位自主着陆方案。文献[5]提出一种基于全局搜索的无人机着陆方法，解决了高空搜索具有显著性视觉效果降落平台的问题。该方法利用含有标志的图像序列进行空地双向检索，提升了降落平台搜索的速度和准确率，缺点是当降落平台在无人机视野外时无人机对降落平台的搜索识别效果不佳。Xu C等[6]提出一种基于检测图像特征点的机载视觉算法，用于控制无人机自主着陆在固定的T型平台上，但该算法实时性不佳且当图像的分辨率降低时着陆精度随之下降。饶颖露等[7]提出一种基于深度学习的无人机自主着陆算法，该算法运行快速、实时性好，但精度不佳，特别是面对光照条件多变和存在多种背景的环境，算法性能出现明显下降。叶利华等[8]提出了一种无人机野外场景识别算法，使用方向梯度直方图(HOG)[9]抓取图像片段的场景特征并据此得到具有空间金字塔特性的特征向量，最后利用支持向量机进行分类。该算法能快速提取出图像局部特征，但识别准确率不高，可能导致无人机自主着陆失败。

针对上述无人机视觉自主跟踪着陆方法存在的问题，设计一种分布嵌入式降落标志(Augmented Reality University of Cordoba，ArUco)[10]作为着陆目标，并提出相应的标志识别和位置解算算法，解决无人机跟踪飞行时目标识别实时性差和定位精度较低的问题；根据无人机跟踪着陆于动态目标的需求提出用于估计目标运动状态的视觉估计算法和分阶段降落策略，以提高无人机稳定跟踪移动目标的能力和自主跟踪着陆的成功率。

1 方法总体框架

本文无人机自主跟踪着陆方法的总体框架如图1所示。

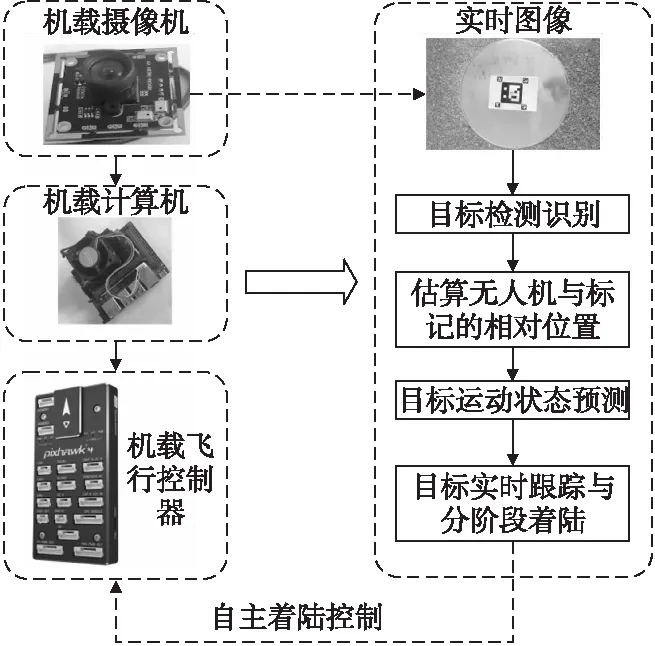
图1 总体框架

在进行自主跟踪着陆前无人机保持悬停。开始着陆任务后，首先将机载相机拍摄的实时图像发送给机载电脑进行处理，检测和识别出着陆平台上的标志并估计无人机与平台中心的相对位置和自身的姿态，然后通过跟踪算法估算出载有着陆平台的无人车的速度，最后将无人车的速度、相对位置和无人机的姿态发送给飞行控制器，控制无人机在目标处于相机的视场中时对无人车保持平稳的跟踪和下降，实现无人机完全自主地跟踪着陆在既定的运动目标上。

2 动态目标识别与定位

2.1 降落标志设计

降落标志可用于辅助无人机视觉定位以及引导无人机自主跟踪着陆。鉴于降落标识的设计需要满足特征足够鲜明、容易被识别的特性，本文设计一种分布嵌入式降落标志作为着陆目标，降落标志如图2所示。

图2 降落标志

该正方形降落标志边长为50cm，其背景为白色，由5个ArUco标记组成，每个ArUco标记都由宽的黑色边框和内部二进制矩阵组成。黑色边框有助于其在图像中的快速检测，二进制编码利于ArUco的识别。内部较大的ArUco标记边长30cm，作为主要的标记辅助无人机定位，外部4个边长为10cm的小标记可以确保在主标记失效时，无人机依然可以确定出特征点并估算与着陆平台的相对位置，增加系统的冗余度。

2.2 目标识别与定位

针对使用视觉标记定位可能存在定位精度不佳的问题，本文基于已有的ArUco视觉定位算法结合上文设计的降落标志提出一种基于ArUco的多标记融合位置解算算法。算法主要包括标记的检测识别和位置的解算两大部分。首先检测出画面中标记的个数，对检测出的标记采用自适应阈值法从灰度图中提取出标记的轮廓，再使用最大类间方差(OTSU)算法[11]提取规范图像中的黑白标志位，将其网格化后统计黑白像素量以确定标记的编号，完成识别。

降落标记的构成元素是正方形，利用PNP(Perspective-N-Point)算法和降落标记的几何特征计算出惯性坐标系中的4个特征点与成像平面中对应的4个像素点的投影关系，进而获得相机与标记的相对位置。PNP算法示意图如图3所示。

图3 PNP算法示意图

图3中H、I、J、K是惯性坐标系下ArUco标记的四个角点，S为ArUco标记的边长，假设四个角点的坐标为H=(-S/2，S/2，0)、I=(S/2，S/2，0)，J=(-S/2，-S/2，0)、K=(S/2，-S/2，0)，各点在成像平面上像素坐标系中对应投影点的坐标为h=(uh，vh)、i=(ui，vi)、j=(uj，vj)、k=(uk，vk)。以H-h映射举例，空间坐标与像素坐标之间的转换关系为

(1)

其中

(2)

(3)

式中：R=[r1r2r3]和t=[t1t2t3]T是相机的外参，即PNP算法所求的旋转矩阵和平移向量；Q是成像平面中的二维像素点向量在相机坐标系下的深度；L是相机的内参矩阵；fx、fy为图像像素坐标系坐标轴的尺度因子；u0、v0为图像像素坐标系中相机光轴投影坐标。通过相机的外参可以将惯性坐标系下的点转换到相机坐标系下表示，为简化计算，暂时不考虑相机内参。设矩阵向量PH=[H1]T，式(1)由式(2)、式(3)可简化表示为

(4)

由式(4)可得到如下两个约束为

(5)

根据式(5)可知，ArUco标记的每个特征点提供了两个关于T的线性约束，而T含有12个未知数，理论上需要6对匹配点解出矩阵T。但旋转矩阵R是单位正交阵，本身具有六个约束为

(6)

根据ArUco标记的四个角点加上旋转矩阵的性质可求得矩阵T，进一步得到矩阵R、t，进而求解出单个ArUco标记在相机坐标系下的坐标。

考虑到相机识别到标记的数目不同，提出解算多个标记进行位置融合的算法。多标记融合示意图如图4所示。

图4 多标记融合示意图

当降落标志中较大的ArUco标记和四个较小的标记都被识别到时，利用PNP算法得出每个标记的中心在相机坐标系下的位置，见图中A、B、C、D、Ow点。由于降落标志被放置在无人车上且无人车的高度不变，可以认为所有降落标记处在一个平面内，将四个小标记中成对角线的两组中心点连接起来，计算出交点P，利用此交点与大ArUco标记的中心位置Ow进行可变权值的加权融合，得到融合后的相机与降落标志的相对位置。

设P点的坐标为(px，py，pz)，Ow的坐标为(owx，owy，owz)，无人机无法识别小标记的最低飞行高度为hmin，融合后的降落标志拟合中心点在相机坐标系下的坐标为(qx，qy，qz)，根据无人机飞行高度high进行的位置加权计算为

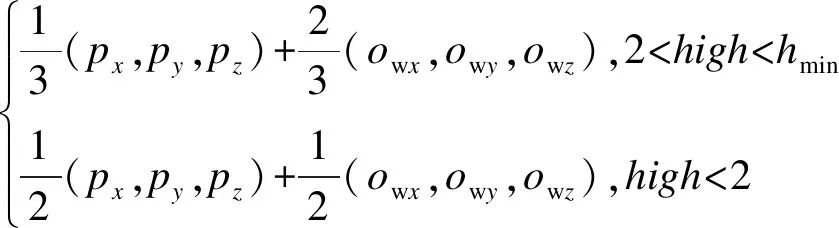
(7)

当出现降落标志中仅有两个较小的ArUco标记被识别到时，降落标志的大部分已经处于相机视野外。连接两个已识别小标记的中心点A、B，进而求出两点的中点。由于本文不考虑无人机的偏航且无人机机头方向与目标前进方向平行，可以根据已知降落标志的长度求出一个虚拟的降落标志中心点。因为文中所用位置融合算法解算频率较高，所以可用解算出的降落标志的位置作为当前位置的估计值，将此估计值与求出的虚拟降落标志中心点加权融合得到降落标志在相机坐标系下的位置。位置融合示意图如图5所示。

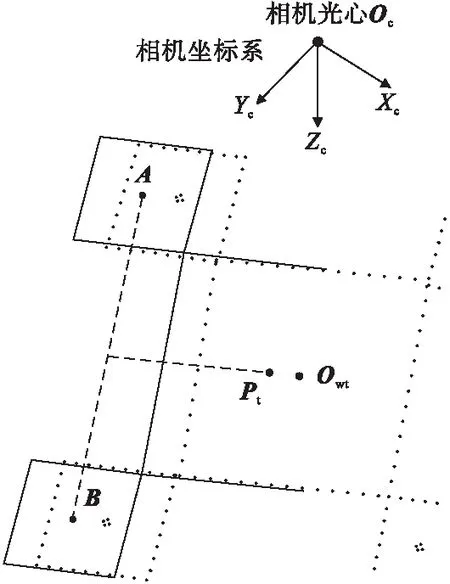
图5 位置融合示意图

以图5所示为例，设点Pt(ptx，pty，ptz)表示根据两个小标记求出的虚拟降落标志中心点，Owt(owtx，owty，owtz)表示解算出的降落标志位置，由Pt和Owt加权融合后的降落标志中心在相机坐标系下的位置(qtx，qty，qtz)为

(8)

位置融合算法的引入提高了位置解算的精度，避免了降落标志被部分遮盖时无法定位的状况。

3 无人机动态目标跟踪降落

3.1 目标运动状态估计与预测

无人机为实现对地面无人车的稳定跟踪需要获得其运动状态，本文根据无人机的运动特性提出一种基于帧间位移差分的速度估计算法，通过主动方式获取无人车的运动状态，速度估计算法示意图如图6所示。

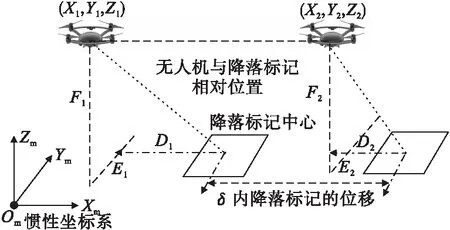
图6 速度估计算法示意图

算法的实现过程如下。

(1)假设机载相机拍摄两张图片的帧间间隔为δ，机载电脑通过读取飞行控制器的里程计信息获取相邻两帧无人机在惯性坐标系下的位置，分别设为(X1，Y1，Z1)和(X2，Y2，Z2)。

(2)根据文中的位置融合以及坐标转换算法可以得到在相机分别拍摄两帧图片时无人机与降落标志中心在惯性系下的相对位置，将两个相对位置表示为(D1，E1，F1)和(D2，E2，F2)。

(3)利用以上的位置量进行差分计算得到降落标志在时间间隔δ内的位移。由于无人车在地面上移动，可不考虑在垂直方向的速度，将此位移与δ求商可估算出目标无人车的速度，设为(Vx，Vy)，计算公式为

(9)

3.2 动态目标跟踪降落

无人机的自主跟踪着陆大多需要降落策略引导其在不同高度飞行，本文中四旋翼无人机需要自主着陆在动态的无人车上，对着陆精度要求较高，考虑到传统的直接降落控制策略存在着陆成功率低、精度差的缺点，本文在对比无人机处于各高度时的可控性后，提出一种分阶段动态降落策略，降落策略的示意图如图7所示。

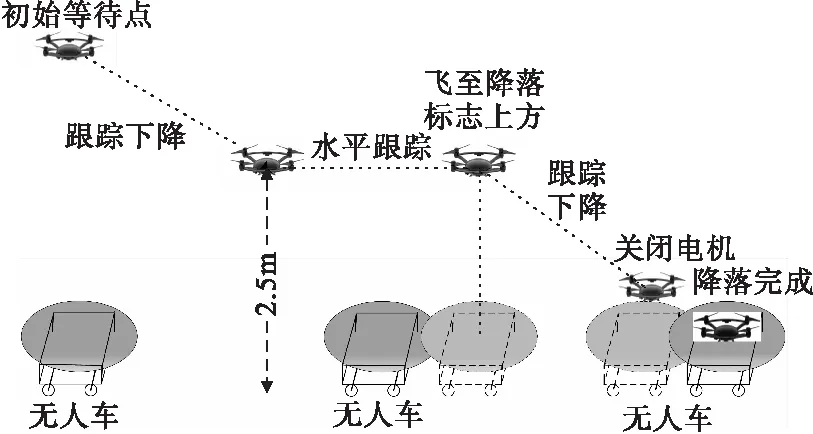
图7 分阶段降落策略示意图

分阶段降落策略的实现过程如下。

(1)无人机在着陆任务的起始点位置悬停保持6～7m的飞行高度并等待搭载降落标志的无人车出现。

(2)当相机识别到目标无人车上的降落标志后，无人机开始跟踪无人车飞行并同时保持恒定的下降速度。

(3)当无人机下降到2.5m左右高度时停止下降并保持水平飞行，跟踪无人车。无人机在跟踪飞行时的速度会比无人车速度稍快，无人机水平飞行一段后会飞至降落标志的上方并以无人车的速度保持跟踪飞行。如果无人机在水平跟踪时发生目标丢失的状况，并且在接下来一段时间内仍然未能有效地识别到降落标志，无人机会保持在当前位置并以0.1m/s的速度上升直到重新捕获目标为止，与此同时无人车会逐步减速到停止，等待无人机重新识别并开始自主着陆。

(4)无人机在无人车上方飞行一段时间，若其能稳定识别降落标志，则开始最后的跟踪着陆。当无人机距离降落平台高度不足20cm时飞行控制程序控制电机停转，无人机自由落体到降落平台上，完成最终的自主跟踪着陆。

4 实验结果与分析

4.1 视觉识别与位置解算

利用机载相机对摆放在不同距离、角度以及复杂环境背景中的降落标志进行视觉检测与识别，以验证降落标志和检测算法的有效性。识别结果如图8所示。

图8 视觉识别结果

图8a为模拟无人机在1.5m、3m和5m高度对降落标志识别结果；图8b是相机与降落标志夹角分别是15°、30°、45°的识别结果；图8c为降落标志摆放在复杂背景中的识别结果。可以看出，视觉算法对摆放在不同高度、角度下的降落标志都能保持有效识别，即使目标在复杂背景中依然能准确识别。以上视觉识别结果表明，无人机搭载相机并运行视觉检测算法识别特定标志、引导无人机自主跟踪着陆的方案具有可行性。

无人机对降落标志进行视觉检测与识别后开始解算自身与目标的位置关系，本文采用将相机固定在某一水平位置并调节不同高度的方式模拟无人机进行位置解算实验，以验证本文提出的多标记融合位置解算算法的有效性。表1和表2为无人机在0.8m和0.5m高度机体坐标系下的位置解算结果。

表1 0.8m高度不同位置解算算法结果对比

表2 0.5m高度不同位置解算算法结果对比

表1和表2中的几组对照数据均为截取多个数据包中相同位置的50组数据进行均值计算的结果，可认为该结果具备一定的代表性。表中单标记解算的数据为仅对降落标志中大ArUco采用PNP算法进行位置解算的结果。从表中数据可以看出，使用多标记融合位置解算算法得到的结果更接近实际的相对位置，当本文降落标志中的5个ArUco标记都被识别到时解算的结果与实际偏差最小，0.8m高度各个方向上的相对误差为(5.0%，6.7%，5.0%)，均小于单标记解算的相对误差(12.5%，16.7%，6.3%)。在0.5m高度时，结果类同。即使文中的嵌入式降落标志有两个较小的ArUco被识别到时，融合位置解算算法的精度也与单标记解算算法的精度相当，在实际使用中这种情况发生时，降落标志大部分已经不在相机视野内，使用单标记位置解算算法无法得到无人机与目标的相对位置，故而多标记融合位置解算算法在无人机进行自主着陆或自主跟踪等任务时位置解算效率及可靠性更高。

4.2 目标运动状态估计

在仿真环境中进行目标运动状态的估计实验，使无人车在平面上沿一个方向匀速或变速前进，并在上位机中运行速度估计程序，估算出目标无人车的速度大小以验证提出的速度估计算法的有效性。无人机主动视觉算法对目标速度的估计与实际速度对比如图9所示。

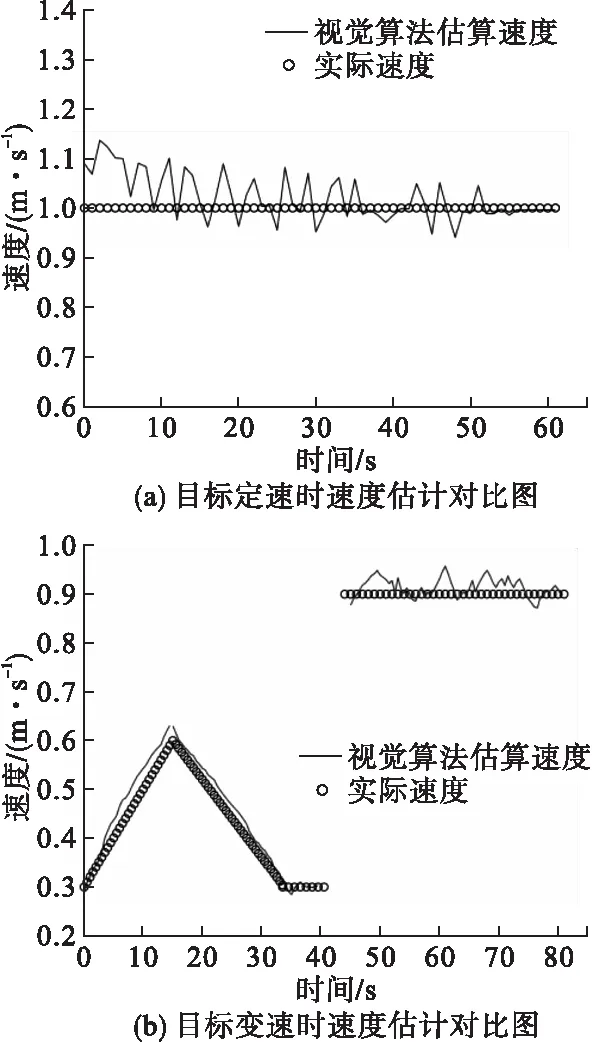
图9 视觉算法速度估计对比图

图9a、9b分别表示目标以1m/s的速度直线前进时视觉算法估计的速度和目标变速行驶时视觉算法估计的速度。图9a中的数据曲线表明当目标无人车以1m/s匀速前进时，文中提出的视觉算法估算出的速度在1m/s附近浮动且估计误差不超过±10%。图9b中无人车先以0.02m/s2的加速度从0.3m/s加速到0.6m/s后再减速回原速度，之后再以0.9m/s的速度匀速前进。从图中的速度估计曲线可以看到，不论无人车加速、减速或者突然改变速度大小，文中提出的基于帧间位移差分的速度估计算法都能有效估算出目标的速度并且误差在可接受范围内。

4.3 动态目标跟踪与分阶段降落

在仿真实验场景中进行目标跟踪着陆实验，自主跟踪着陆实验效果如图10所示。

图10 自主跟踪着陆实验效果图

首先，无人机起飞并飞向仿真环境中的指定位置，当地面无人车进入无人机视野中靠近中心位置，机载电脑中的程序向飞行控制器发送指令并将无人机切换到自主跟踪着陆模式，无人机跟踪并逐渐靠近无人车的同时降低飞行高度，采用分两阶段降落的策略平稳着陆在无人车上。

在仿真实验环境中多次进行动态自主着陆实验，记录无人机的飞行轨迹、着陆的成功率和着陆误差等数据，并与通过直接降落策略获得的数据进行比对分析。两种策略下自主跟踪着陆飞行轨迹(惯性坐标系)如图11所示。

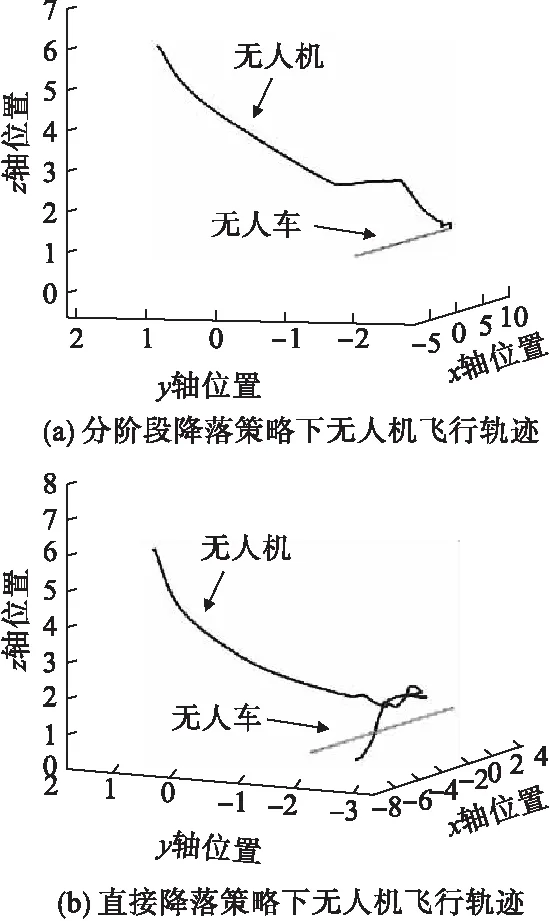
图11 不同降落策略下无人机飞行轨迹

根据图中的轨迹可知，无人机从惯性坐标系下的(-6m，1m，6m)位置开始进行自主动态跟踪着陆。图11a中无人机采用分阶段降落策略，从初始位置平稳下降，接着保持水平飞行不断跟踪靠近无人车，最终两条轨迹相交，无人机平稳着陆。图11b中，由于采用直接降落的策略导致初始阶段无人机飞行轨迹很陡，飞行姿态不稳定，易失控坠毁。本文提出的分阶段降落策略相较于常用的直接降落策略，无人机飞行姿态更为稳定，下降过程更为线性，提升了自主着陆的成功率与精度。

5 结论

提出一种应用于空地异构系统的无人机自主跟踪着陆方法，设计了嵌入式降落标志并通过视觉算法实现了目标检测识别功能，通过标记融合算法实时解算无人机与目标的相对位置；提出了一种图像帧间位移差分算法估计目标的运动速度用于跟踪目标飞行；为达到无人机更稳定的着陆效果，提出了一种分阶段动态降落策略引导无人机在不同高度飞行，实现了四旋翼无人机在移动无人车上的稳定着陆，通过实验验证了提出算法和策略的有效性。提出的目标跟踪着陆方法仅限于对速度小于2m/s的动态目标进行着陆且没有考虑地面效应对无人机着陆造成的影响，后续将进行改进以满足无人机在高速目标上着陆的要求以及开展旋翼无人机克服地面效应影响的研究。