径向金属密封唇部结构接触力学研究*

杨仪伟 张 津 何东升 许亮斌

(1.西南石油大学机电工程学院 四川成都 610500；2.石油天然气装备技术四川省科技资源共享平台 四川成都 610500；3.宝石机械成都分公司川石油气密封件厂 四川成都 610000；4.中海油研究总院有限责任公司 北京 100028)

径向金属密封唇部是实现密封的核心部位，唇部的受力和变形状况对于密封起着决定性的作用。因此，必须合理地设计径向金属密封的唇部结构，并建立其接触力学模型，研究唇部结构参数对其接触应力、最大Mises应力和接触宽度的影响。

赫兹针对无摩擦弹性接触问题创立了接触理论，之后众多学者研究了有摩擦、弹塑性、黏弹性、承受集中力和椭圆压力分布的接触问题并给出了解析解[1-2]。学者们还基于有限元法研究了二维光滑接触、二维轴对称摩擦接触、静态摩擦接触、动态摩擦接触和动态摩擦大变形接触等问题[3-4]。

金属密封圈能够满足井下安全工作条件的要求，因此在一些油气井作业中得到了广泛的应用[5-6]。金属密封圈利用柔性金属密封圈作为外密封件与内密封件相接触，形成紧密耐用的密封副，能够承受油气井的高温、高压和腐蚀性流体条件[7]。2006年，LEE等[8]利用数值模拟与试验研究了轴与密封圈在不同过盈配合下的密封端面宽度和密封唇口的接触压力。2014年，陈晓芳等[9]基于理论和仿真研究了水下卧式采油树井口连接器VX钢圈接触应力特性。2014年侯超等人[10]基于有限元法分析了水下井口系统中使用的环形金属密封组件的密封机理和工作原理。2014年李玉婷等[11]基于有限元仿真建立和改进了U形金属密封圈的二维轴对称模型。2014年，崔晓杰等[12]利用有限元方法研究了井下金属分层隔离工具的密封原理。2016年，彭粲粲等[13]基于数值模拟提出了油管悬挂器K形密封的二维轴对称模型。2016年，WEI等[14]分析了海底管道机械接头密封面密封机制，并基于弹性叠加原理得到了密封的临界条件。2015年张凯等人[15]和2017年秦桦等人[16]仿真研究了海底采油树油管悬挂器K形金属密封环在实际工况下的密封机制。

本文作者结合现有的接触力学理论和非线性有限元方法研究径向金属密封唇部结构的接触力学行为，探索接触力学参数与结构参数之间的关系，并建立径向金属密封和强度设计要求。

1 径向金属密封唇部接触力学模型

径向金属密封唇部是实现密封的核心部位，唇部的受力和变形状况对于密封起着决定性的作用。一方面，接触载荷要使得径向金属密封的最大Mises应力足够小以保证其始终处于弹性变形状态；另一方面，唇部所受到的接触载荷要使得接触应力和接触宽度足够大以保证不发生泄漏。因此，必须合理地设计径向金属密封的唇部结构，并建立其接触力学模型，研究唇部结构参数对其接触应力、最大Mises应力和接触宽度的影响。

1.1 径向金属密封原理

如图1所示，为了隔离井底油套环空和油管之间的油气通道，在井下流量控制阀(ICV)壳体和滑套之间采用组合径向金属密封圈来实现密封。该组合径向金属密封圈由径向金属密封件和非金属密封件组成。非金属密封件用于将井底压力传递给径向金属密封件，还起到辅助密封的作用。当滑套沿轴向下移动时，径向金属密封件和非金属密封件的唇部会在初始过盈量和压差下沿径向接触并挤压滑套的外圆柱面；两者组成的径向金属密封副发生弹性变形并产生接触应力，形成有足够接触宽度的圆环状接触带，阻断井底流体在一定压差下的流动，直到滑套到达径向金属密封底座处，此时井下流量控制阀关闭。而当滑套向上移动时，径向金属密封件将继续保持密封作用，直到上部的非金属密封件与滑套脱离接触，此时井下流量控制阀开启；当滑套继续向上轴向运动以遮挡不同数量的节流孔，此时井下流量控制阀以一定的开度实现节流。

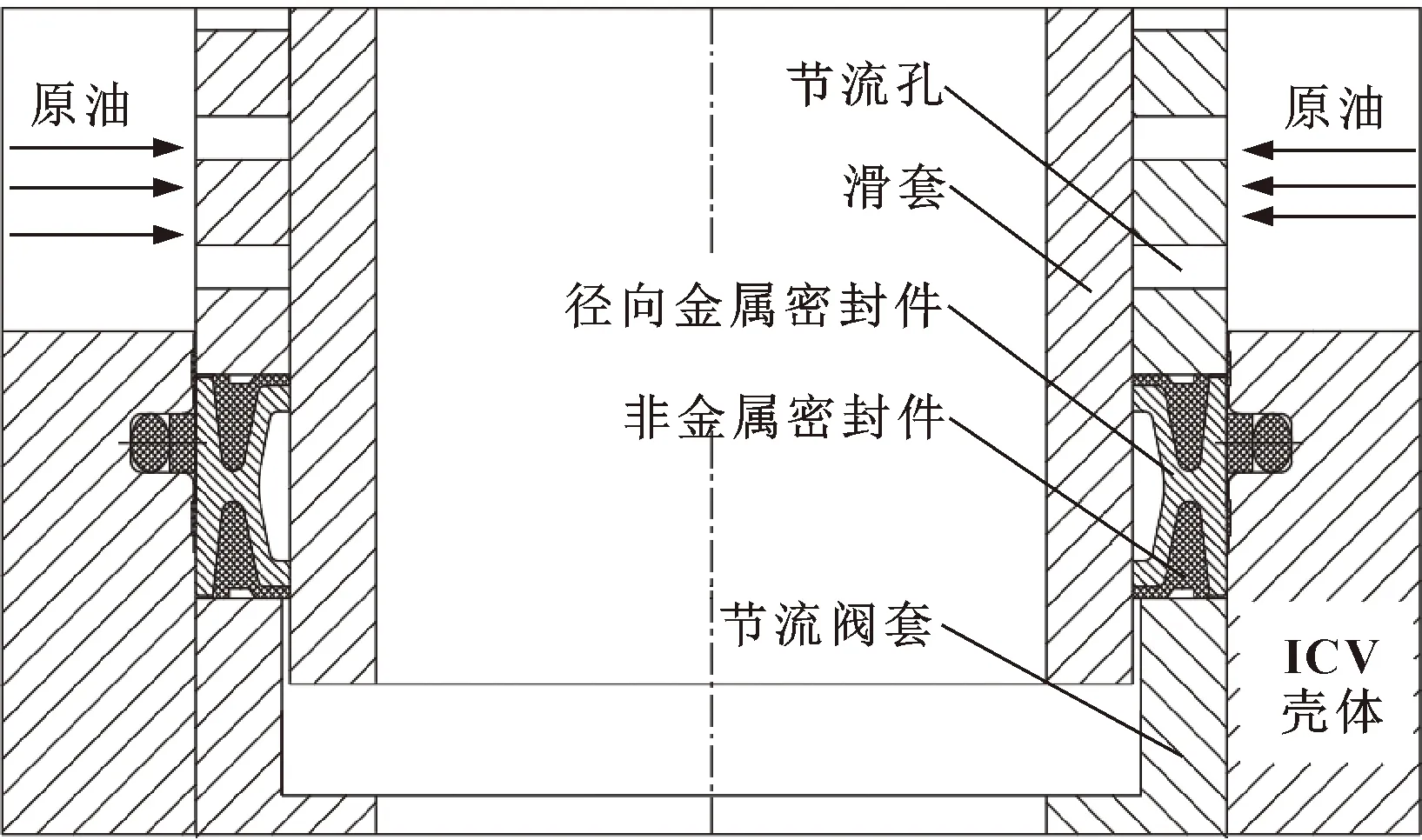
图1 ICV中的组合径向金属密封圈结构

径向金属密封的相关材料性能如表1所示。径向金属密封元件由高温镍基合金GH4169制成。该合金具有良好的高温强度、优异的抗蠕变和抗疲劳性能、优异的加工和焊接性能，在工业领域应用广泛。非金属密封件可由氟橡胶材料制成，氟橡胶具有耐热、耐油、抗氧化、耐腐蚀等优点。滑套由碳化钨硬质合金材料制成。

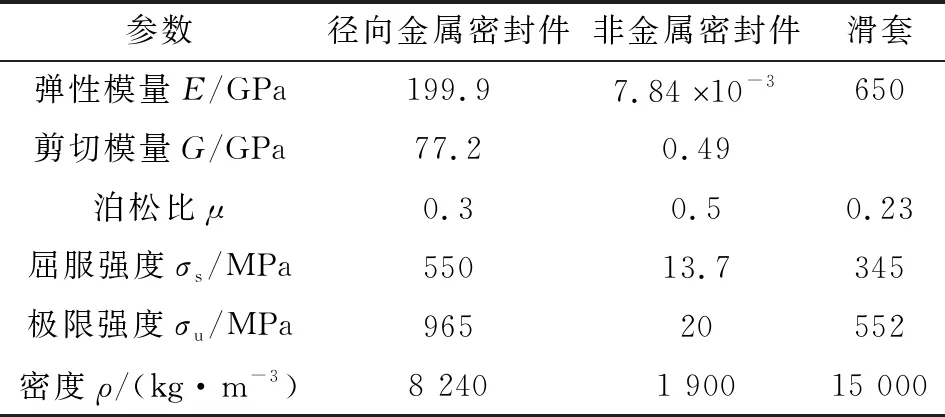
表1 组合径向金属密封副的材料参数

1.2 径向金属密封唇部接触力学模型

径向金属密封件唇部与滑套外表面的接触属于圆柱内外表面协调弹性接触。由于径向金属密封件的长度有限，在径向金属密封件唇部上下两端处会发生接触应力集中，这将引起塑性变形，从而导致两者密封接触面的泄漏而使得密封失效。因此，必须对径向金属密封件唇部的轮廓形状进行合理设计，以消除接触应力集中。为了减小加工成本，降低加工难度，将其设计成曲率半径为R1的圆弧，如图2所示。图中，B和2a分别为径向金属密封圈的理论和实际宽度，c为径向金属密封圈的径向厚度，Fp为径向金属密封圈处的接触载荷，R2为滑套的曲率半径。如此，将径向金属密封唇部的协调弹性接触转变成为轴对称的平面与圆弧的非协调性接触，实现了较小的接触力获得较大的接触应力，还能保证接触力始终沿着圆柱面的外法线方向，避免径向金属密封件唇部结构发生塑性变形。

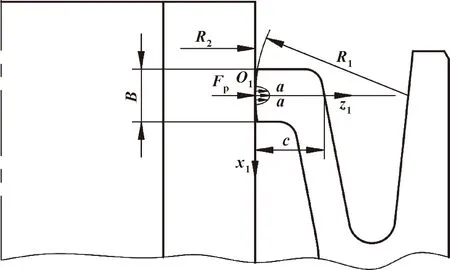
图2 径向金属密封件唇部接触模型示意

径向金属密封唇部弹性变形足够小，故可以使用线性小变形弹性理论；并且接触区域的有效尺寸相对于径向金属密封唇部的尺寸和表面的相对曲率半径要小得多，通过将径向金属密封唇部看作是以平表面为界的弹性半空间，来近似计算接触应力。此时，径向金属密封唇部可以理想化为一个半无限圆面与半无限平面的接触，如图3所示。取界面上的法向力沿平行于z轴作用，而取切向力作用在x-y平面内[7]。

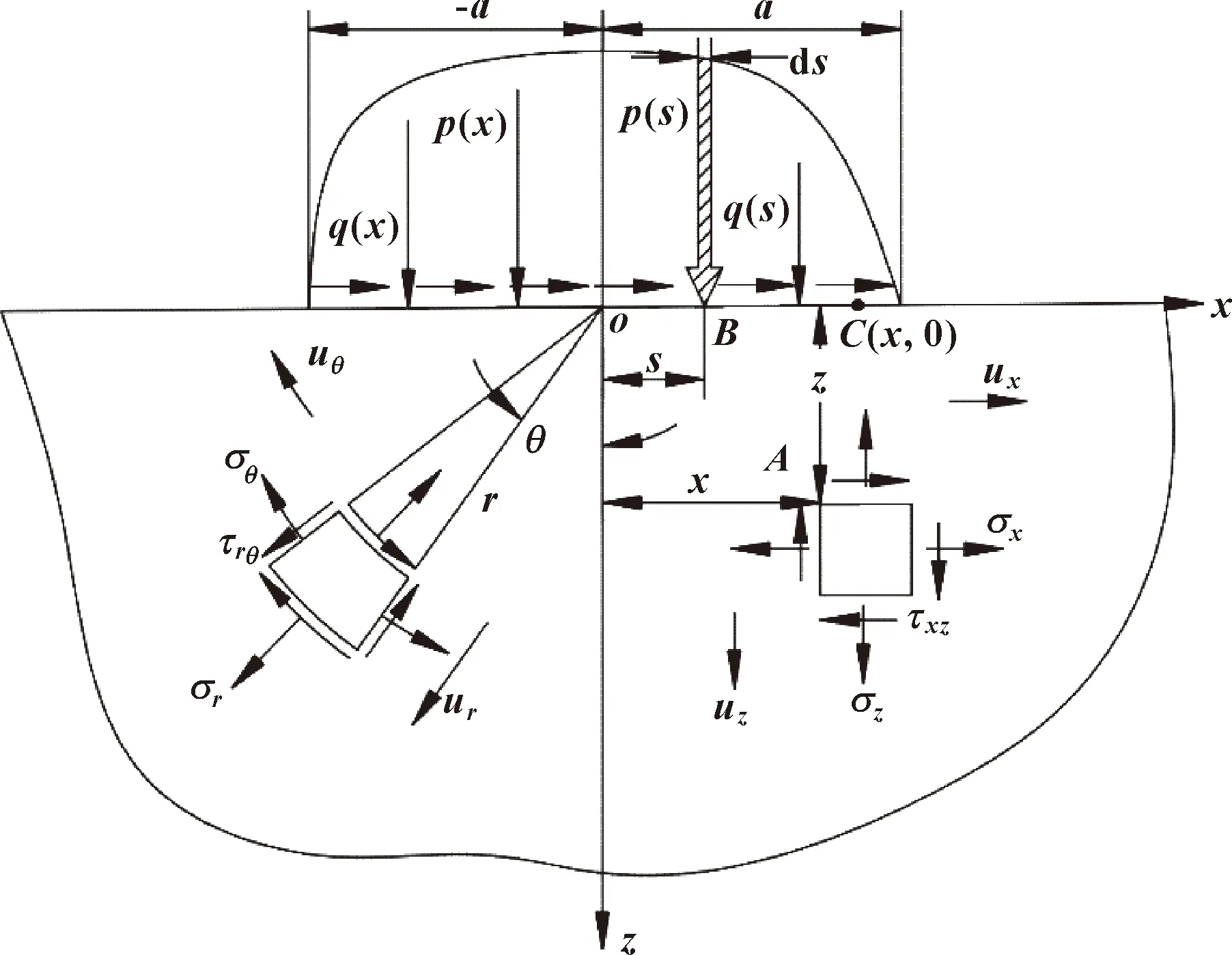
图3 弹性半空间的线载荷

半无限空间物体表面处的位移梯度为

(1)

如图4所示，当两圆柱体轴线均与y轴平行，受到单位长度上的分布力Fp压缩而形成二维接触，在平行于y轴、宽度为2a的长条上接触，间隙h为

图4 两圆柱体非协调接触模型

(2)

式中：相对曲率1/R*=1/R1+1/R2;z1、z2为圆柱体表面未接触前两点的坐标。

对于滑套来说，有R2=0。接触区内的点：

(3)

将式(3)对x求导可得：

(4)

作用在-a≤x≤a的长条上的压力p(x)所引起的表面梯度在每个圆柱面上的压力相等，可得：

(5)

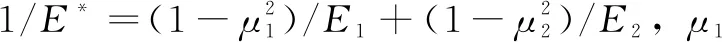
则可得下式：

(6)

解得：

(7)

经分析可得，半接触宽度a、应力分布p(x)、最大接触应力σmax和平均接触应力σave表达式为

(8)

(9)

(10)

(11)

则沿z轴积分可得应力分量：

(12)

平面应变下，圆柱物体内部某点的位移为

(13)

在图2、3所示的坐标系x1O1z1中，c为径向金属密封件唇部径向厚度，当从z1=0到z1=c时将εz积分便得到点O1的压缩量δ：

(14)

将式(14)积分可得：

(15)

式中：压缩量δ为径向金属密封副的初始过盈量。

真实密封接触线的宽度为w，该接触线绕轴对称中心线旋转一周成为圆环带状的接触环面，该圆环带状的接触面就是径向金属密封副阻绝流体泄漏的密封面。径向金属密封接触面有2个关键的接触力学参数：接触应力分布p(x)和接触宽度w。这2个接触力学参数与密封面的接触载荷和径向金属密封件唇部圆弧结构的受力变形有关，同时也与径向金属密封件整体结构和几何尺寸有关。因为径向金属密封副是径向金属密封件唇部内表面与滑套的外圆柱面的直接接触构成的，不便于利用试验直接测量接触应力分布和接触宽度，但是可以利用有限元软件仿真分析接触应力分布和接触宽度。

2 径向金属密封唇部接触力学模型数值验证

建立径向金属密封唇部的有限元模型，来验证接触力学理论模型。选取8个指标开展验证分析：密封面的接触宽度w，最大接触应力σmax，初始过盈量δ，平均接触应力σave，3个主应力和Mises应力。

如图5所示，利用ABAQUS软件建立井下流量控制阀径向金属密封件唇部结构与滑套轴对称的模型。其中滑套内径60 mm，外径80 mm，相关材料参数见表1。为径向金属密封件施加均布压力，再乘以径向金属密封件唇部的轴向厚度B即为名义接触载荷Fp。通过为滑套施加径向位移载荷来模拟径向金属密封副的初始过盈量。

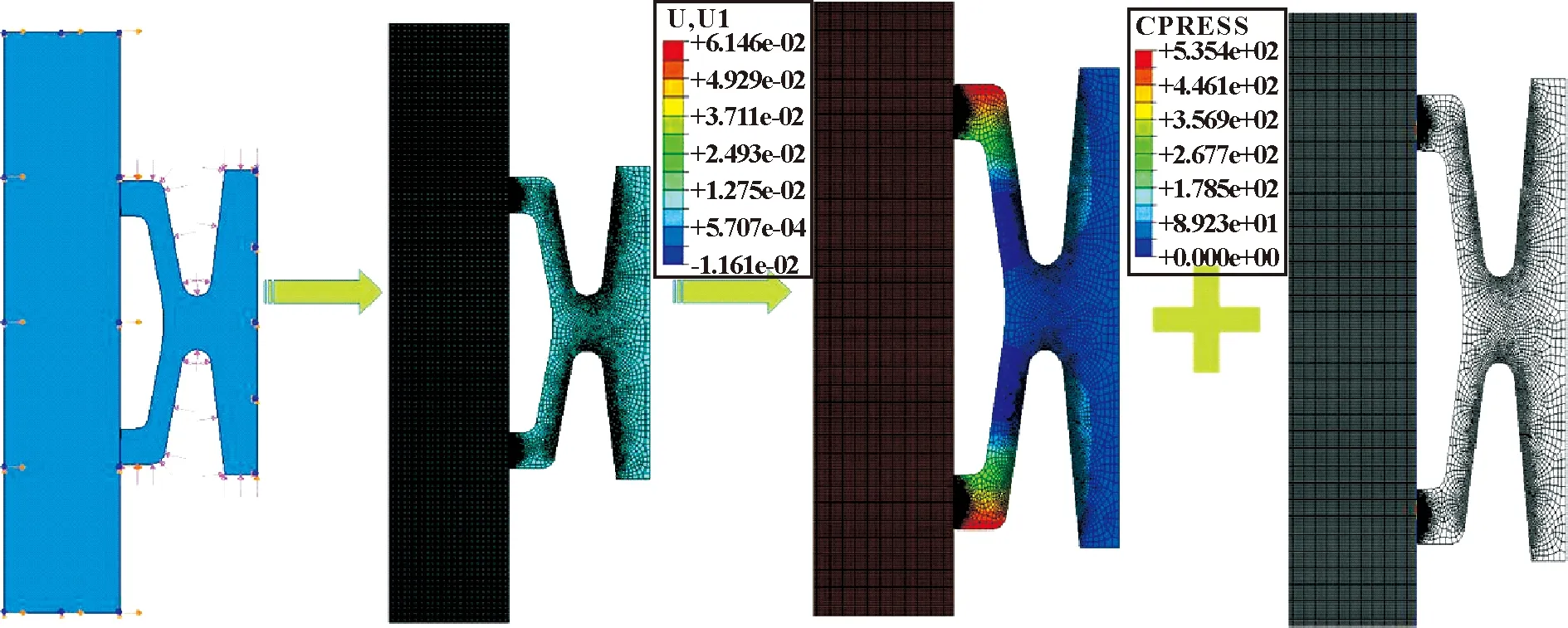
图5 径向金属密封唇部有限元分析流程

利用公式(8)—(11)、式(15)和有限元仿真方法，计算最大接触应力、平均接触应力、接触宽度和初始过盈量的理论解与数值解。如图6—9所示，随着接触载荷的增加，最大接触应力、平均接触应力、接触宽度和初始过盈量均增加，2种方法给出的计算结果增长趋势一致，而且大小相近。

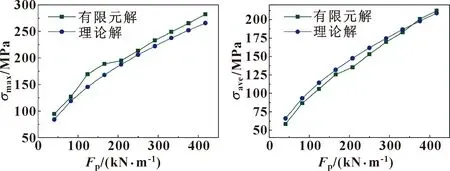
图6 σmax与Fp关系

图8 w与Fp关系

如图10所示，接触宽度的理论解与数值解的平均相对误差为8.86%；最大接触应力的理论解与数值解的平均相对误差为6.96%；初始过盈量的理论解与数值解的平均相对误差为8.88%；平均接触应力的理论解与数值解的平均相对误差为4.33%，误差在工程上均可接受。图11给出了不同接触载荷作用下的接触压力分布，沿密封面上各接触点的接触应力分布形式为椭圆曲线，符合赫兹接触理论。

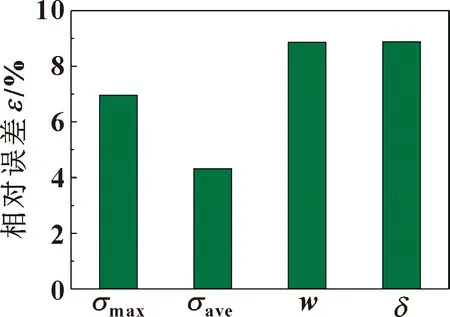
图10 理论解与数值解相对误差

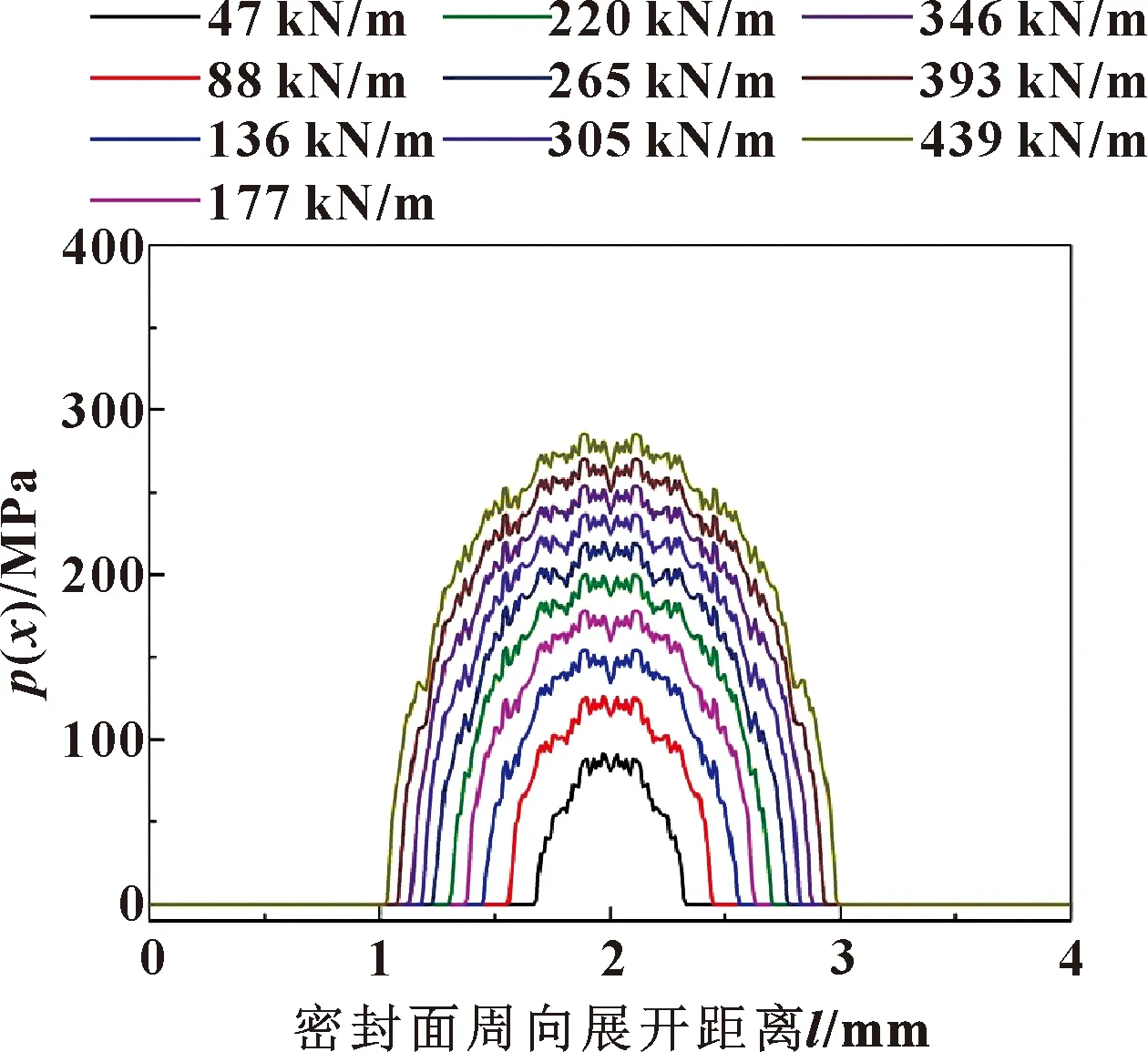
图11 不同接触载荷下接触应力分布

在不同的接触载荷的作用下，利用式(12)计算图3中O1z1轴上各点的3个主应力和Mises应力的理论解，并提取O1z1轴上各点的Mises应力和3个主应力的有限元解，如图12—19所示。

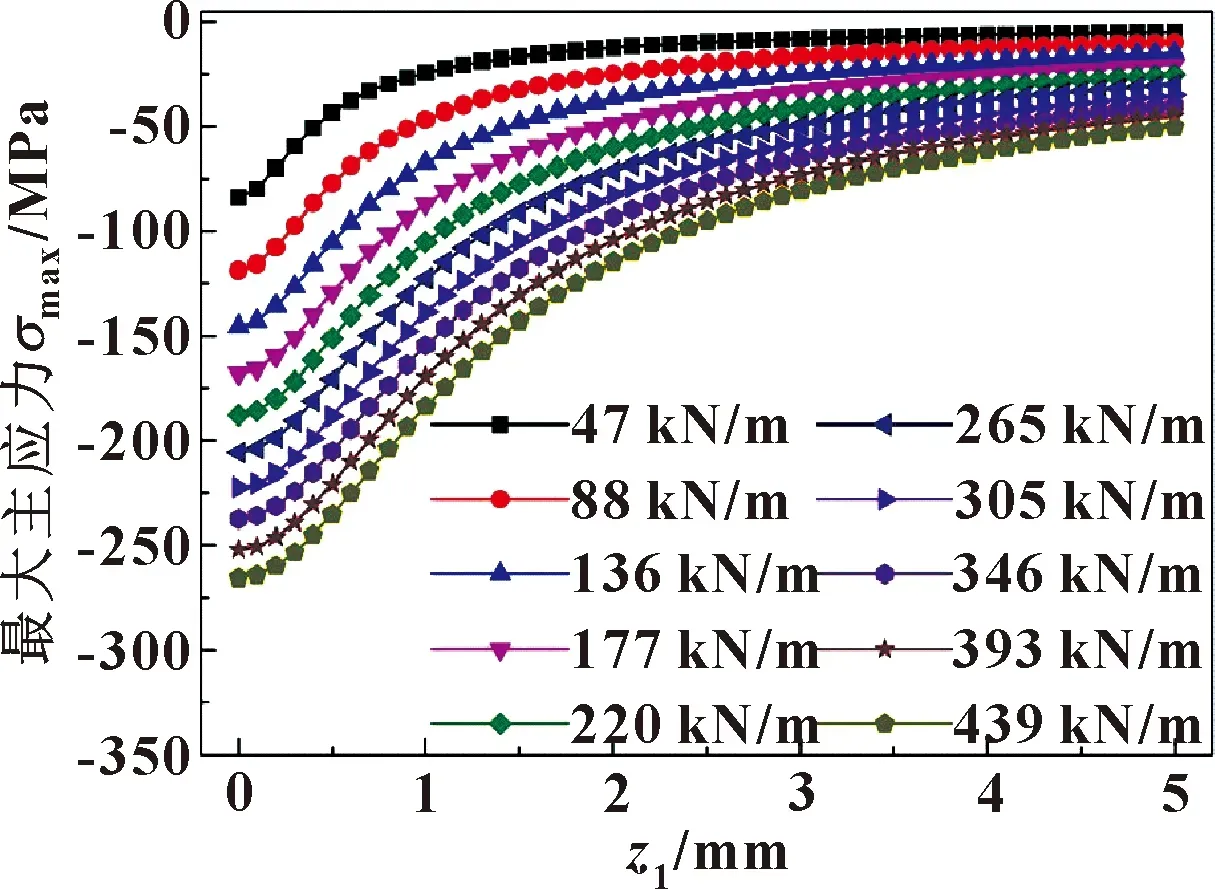
图12 不同Fp时最大主应力理论解

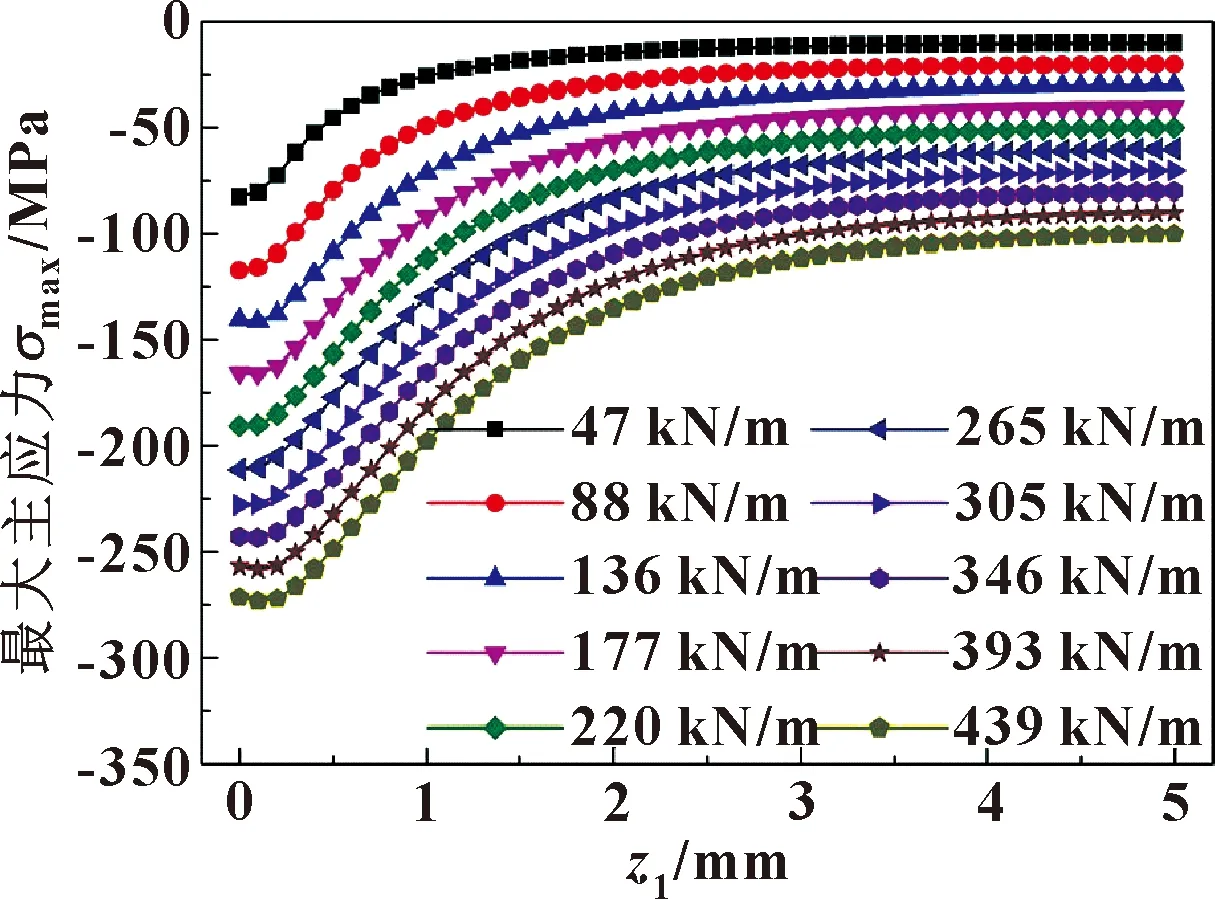
图13 不同Fp时最大主应力数值解

图14 不同Fp时中间主应力理论解

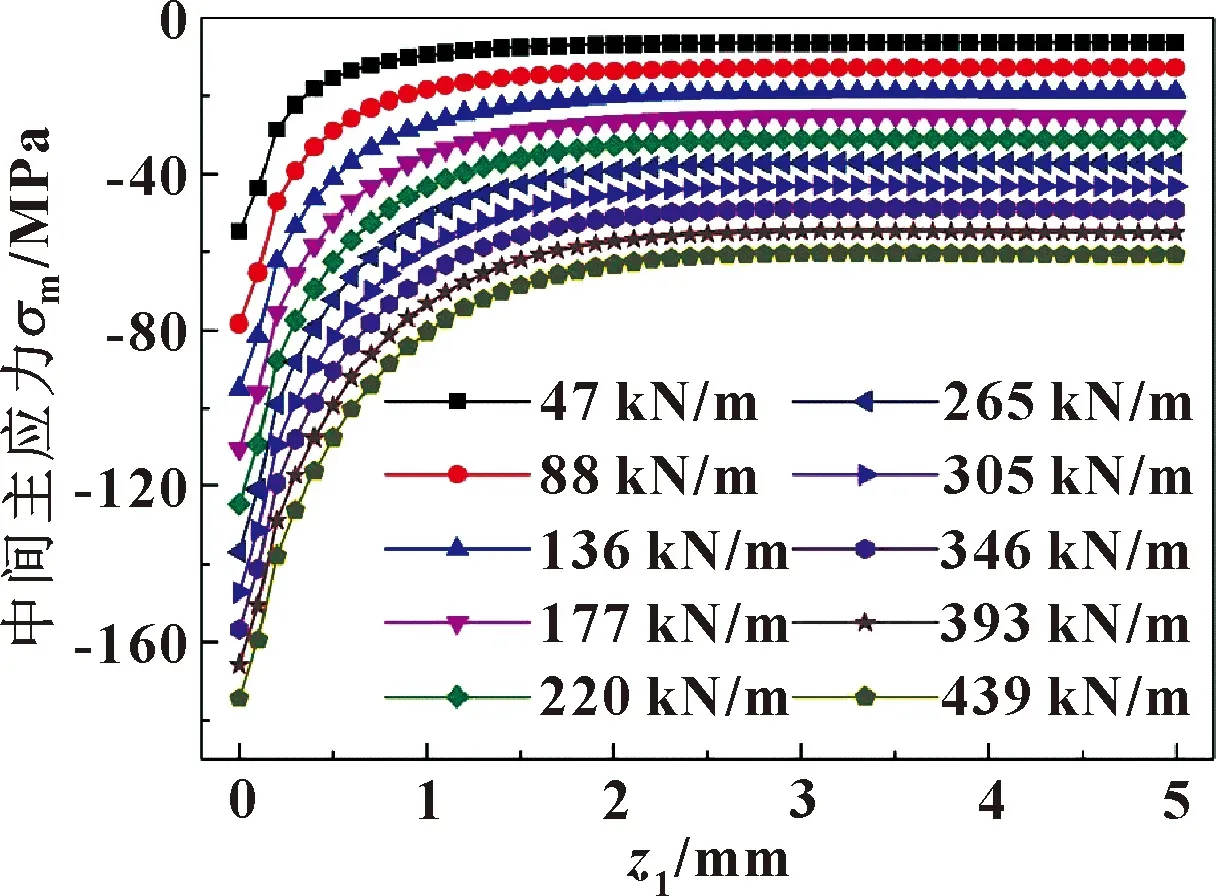
图15 不同Fp时中间主应力数值解

图16 不同Fp时最小主应力理论解

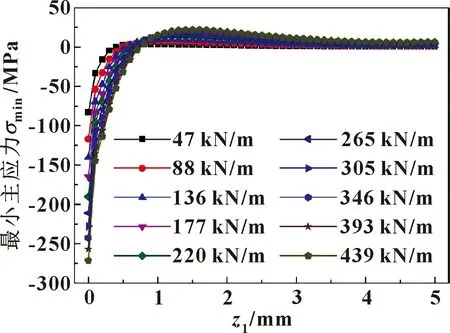
图17 不同Fp时最小主应力数值解

如图12、13所示，随着z1的增加，当接触载荷为136 kN/m时，最大主应力值的理论解从-145.58 MPa增加到-15.2 MPa；而最大主应力值的有限元解从-135.19 MPa增加到-28.02 MPa。如图14、15所示，随着z1的增加，当接触载荷为136 kN/m时，中间主应力理论解从-87.35 MPa增加到-4.57 MPa；而中间主应力值的有限元解从-90.78 MPa增加到-18.5 MPa。如图16、17所示，随着z1的增加，当接触载荷为136 kN/m时，最小主应力值的理论解从-140.19 MPa增加到-2.41 MPa；而最小主应力值的有限元解从-138.32 MPa增加到-2.34 MPa。可见，随着z1的增加，3个主应力应力的理论解和有限元解都快速增加并趋于一定值。

如图18和19所示，随着z1的增加，当接触线载荷为136 kN/m时，Mises应力值的理论解从55.34 MPa增加到78.25 MPa，然后减小到11.95 MPa；而Mises应力值的有限元解从54.78 MPa增加到92.46 MPa，然后减小到26.14 MPa。Mises应力的理论解和有限元解都先快速增加后逐渐减小，最后趋于一个稳定值。

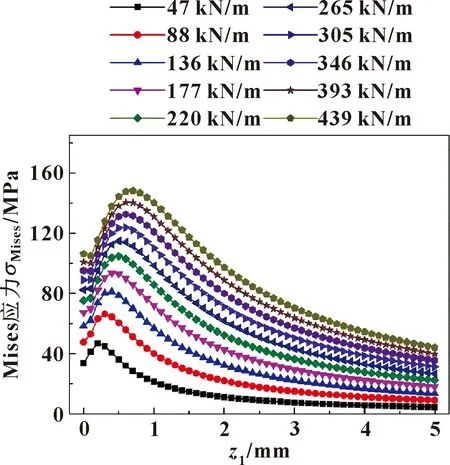
图18 不同Fp时Mises应力理论解

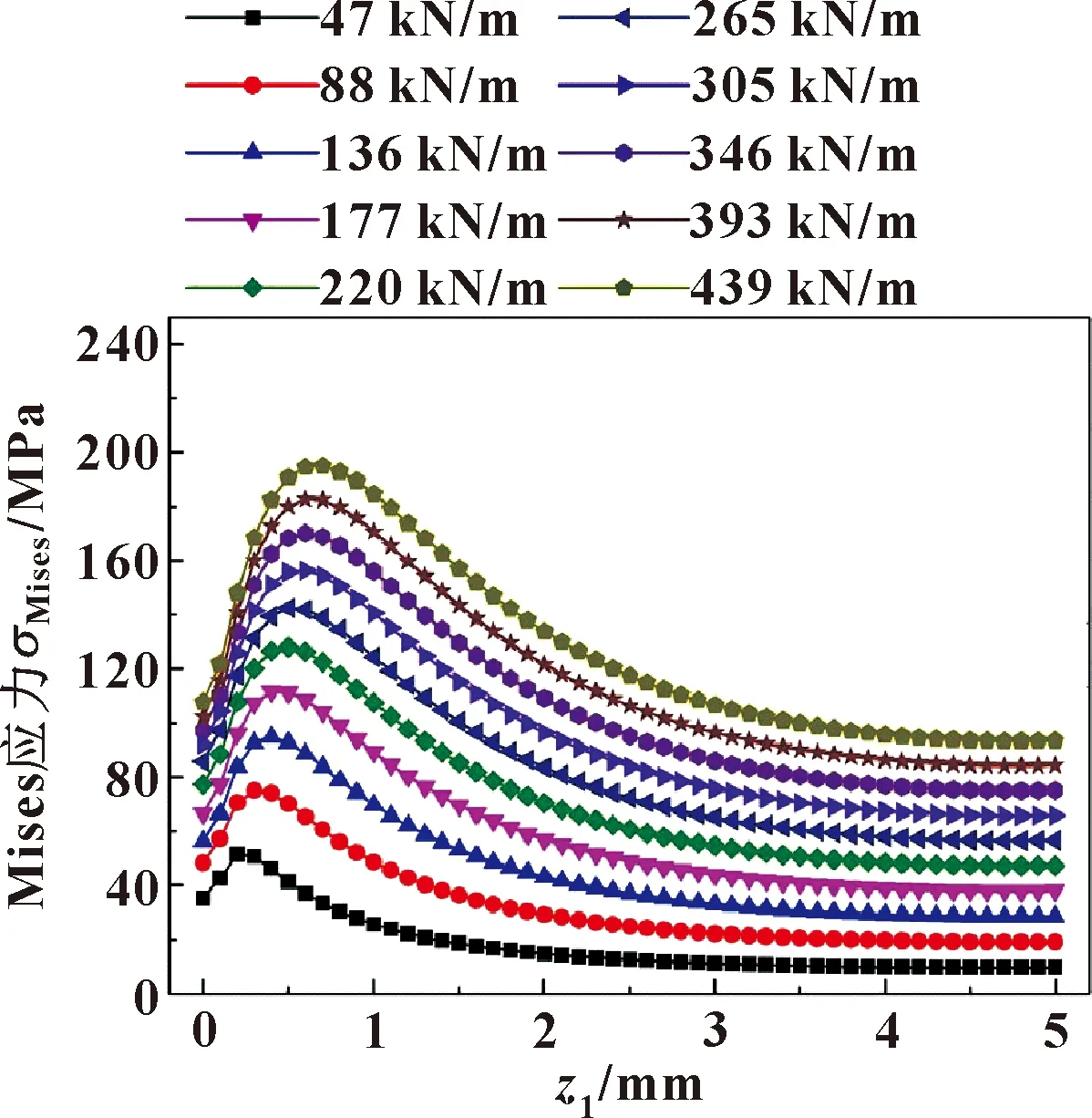
图19 不同Fp时Mises应力数值解

如图20所示，坐标系x1O1z1原点处的3个主应力值和Mises应力的理论解和有限元解的绝对值都随着接触载荷的增加而增大。如图21所示，各应力的理论解和数值解之间的相对误差均小于10%，因此认为各应力的理论解和有限元解吻合得很好。

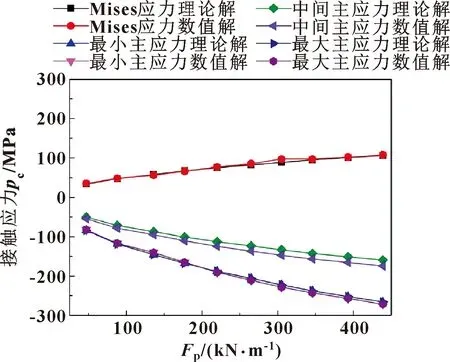
图20 x1O1z1坐标系原点各应力值

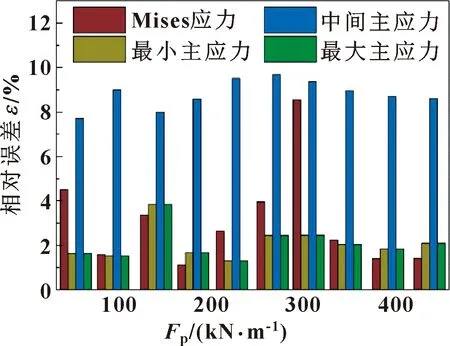
图21 x1O1z1坐标系原点各应力相对误差

3 径向金属密封唇部参数关系分析

根据式(15)、(10)和(8)，研究最大接触应力与δ、R1、c、B4个设计参数的关系。其中，δ=0.05～0.15 mm，R1=350 mm，介质压力为20～40 MPa，材料参数如表1所示，最大接触应力与径向金属密封唇部参数的关系如图22—25所示。

如图22所示，最大接触应力随着初始过盈量的增大而增大;当初始过盈量为0.14 mm、介质压力为40 MPa时，最大接触应力为346.7 MPa，大于179.3 MPa，且小于接触应力上限655 MPa。此时的接触宽度为1.878 mm，大于最小接触宽度1.058 mm，满足密封和强度设计要求，可以实现可靠的密封。

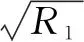
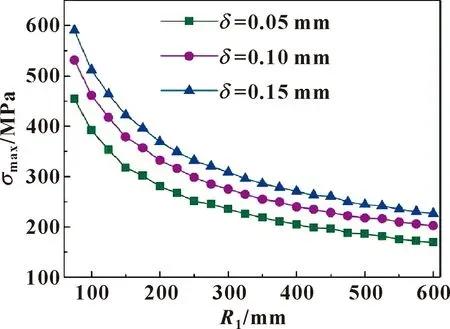
图23 不同初始过盈量下最大接触应力σmax与R1关系

如图24所示，密封面上最大接触应力随着径向金属密封径向厚度的增加而增加，这是因为增加径向金属密封径向厚度也就增加了其刚度，使其难以压缩变形从而增加了最大接触应力。但是径向厚度c的增大也将引起径向金属密封整体尺寸的增加。所以，应尽量减小径向金属密封件的径向厚度尺寸。

图24 不同初始过盈量下最大接触应力σmax与c的关系

如图25所示，在初始过盈量相同时，最大接触应力随着径向金属密封件唇部轴向厚度B的增加而增大。这是因为径向金属密封件唇部轴向厚度B的增加的同时也增加了其唇部的刚度，刚度越大压缩变形越困难，最大接触应力也越大。所以，应尽量增加径向金属密封件唇部轴向厚度，既保证较大的实际接触宽度又可以保证较大的最大接触应力。

图25 不同初始过盈量下最大接触应力σmax与B的关系

4 结论

(1)基于接触力学和非线性有限元分析研究径向金属密封唇部的接触力学行为，提出径向金属密封唇部的圆弧结构，基于接触理论建立了径向金属密封唇部轴对称结构的圆弧-平面接触模型，得出了径向金属密封唇部结构接触力学参数的理论关系式，发现径向金属密封唇部的最大接触应力与初始过盈量、径向金属密封唇部径向厚度和轴向厚度成正比，与径向金属密封唇部圆弧半径成反比。

(2)基于模型得到的径向金属密封唇部接触力学参数的理论解与数值解相符，接触宽度、最大接触应力、初始过盈量和平均接触应力的平均相对误差分别为8.86%、6.96%、8.88%和4.33%，在工程上均可接受。