超低温弹簧蓄能密封圈动密封性能有限元分析与优化设计*

王 帅 李 莹 陈 涛 王喜良

(1.清华大学航天航空学院 北京 100084；2.蓝箭航天技术有限公司 浙江湖州 313000)

密封在当代工业的各个领域都有着非常重要的应用，如汽车、船舶、机床、核能、航空航天等。弹簧蓄能密封圈，又称泛塞封(下文简称泛塞封)，是一种具有特殊结构的密封件[1]。泛塞封一般由夹套以及金属蓄能弹簧构成，其中夹套材料一般选用具有耐低温、耐腐蚀、摩擦因数低等特点的PTFE等非金属材料[2]。泛塞封具有高压下自密封，在大温度范围、很大压力范围内保证良好密封性能的特点，目前已广泛应用于汽车、船舶、天然气、航空工业等领域，在LNG工业的加注枪阀杆中大量使用[3-5]。但泛塞封尚未广泛应用于液体火箭发动机。蓝箭航天研制的天鹊系列液氧甲烷发动机中，将弹簧蓄能密封圈应用于低温阀门，成功解决了阀门在低温、高压、往复和旋转运动中的动密封难题，满足了高可靠、低成本、快速迭代的发展需求。

目前对泛塞封的研究主要针对原材料分析、磨损寿命试验和压力试验等[6]，但由于长周期、高成本，很难满足客户需求[7]。而应用有限元等数值计算法分析则比试验研究具有成本低、效率高、数据全面等优势。兰晓冬等[8]利用仿真软件分析了采油树节流阀泛塞封的密封性能，其分析模型忽略了蓄能弹簧。这种二维简化模型同样也被臧平[9]与梁栋[10]应用于研究超高压(>100 MPa)下的节流阀中泛塞封的动、静密封性能。但是在很多工作环境下，泛塞封蓄能弹簧的影响不可忽略。贾晓红等[11]与田乾等人[12]建立了泛塞封三维的有限元模型。但由于三维模型的计算成本较高，为了合理地使用二维简化模型并考虑螺旋非轴对称弹簧的影响，JIA等[13]将蓄能弹簧的作用等效为作用在夹套内壁的恒定载荷。贾晓红等[14-16]进一步提出使用等效的二维轴对称弹性圈代替蓄能弹簧的数值模型，并利用该模型分析了压缩率、等因素对密封特性的影响。李小芬和叶小强[17]应用该模型研究了低温下泛塞封的密封性能。

有限元数值仿真方法便于对模型结构进行优化设计，相比传统优化设计流程可以省去很多加工、试验的周期与成本。田乾等人[12]研究了滑环顶部宽度、唇面半径等参数对密封性的影响；臧平[9]优化了泛塞封的唇前与唇后与壁面夹角；李坤[16]则对密封圈底座的高度尺寸与构型进行了优化，降低对极限位移和最大静摩擦力的影响；高涵宇[18]针对U形密封圈的几何形状抽象出4个参数，为结构优化设计提供指导。

尽管泛塞封技术经过几十年的发展已取得了非常丰硕的成果，但在对超低温工况下完整密封系统的有限元仿真分析上依然需要进一步的研究[4]。本文作者针对某型号弹簧蓄能密封圈建立等效二维轴对称仿真模型，并对泛塞封装配过程的2种不同方法进行比较与分析。对泛塞封在常温与超低温下不同介质压力环境下的动密封性与摩擦力进行计算，重点分析超低温环境下泛塞封性能与常温下的异同。针对模拟结果，提出3种泛塞封性能优化方案，并从密封性能、摩擦性能以及强度寿命3个方面对优化方案进行评价。

1 弹簧蓄能密封圈有限元模型

1.1 几何模型

如图1所示为文中分析的泛塞封的二维截面示意图，密封圈的几何参数见表1。其中过盈量的内外非对称性是由内外唇的厚度导致的，外唇的厚度比内唇厚0.1 mm。提供这样的初步设计的依据有两方面：其一，在低温环境下外径的收缩量更大，较大的过盈量可以提供足够的收缩余量；其二，外唇的过盈量不会对滑动轴上的摩擦力有直接的影响。

图1 泛塞封几何模型

表1 密封圈几何模型尺寸 单位：mm

1.2 等效轴对称有限元模型

泛塞封模型的几何形状、边界条件及滑动轴对夹套的摩擦载荷都具有轴对称性。蓄能弹簧为双螺旋几何结构，故选用一个等效刚度的弹簧模型替代双层螺旋形弹簧[14]。等效弹簧模型保证外径以及材料参数与实际使用的螺旋弹簧一致，通过修改等效厚度保证其在工作压缩范围内的弹簧反力与真实弹簧试验值近似。

通过数值试验测得弹簧圈在工作过程中的压缩量在0.35 mm以内。在等效弹簧圈两侧设置刚性平面，固定下平面，准静态下压上平面，如图2所示。对弹簧的等效厚度进行数值试验，如图3所示，当弹簧的等效厚度设置为e=0.082 mm时其压缩反力以及压缩弹性势能与试验值比较接近，故该模型选用厚度为0.082 mm的轴对称弹簧圈代替。

图2 等效轴对称弹簧模型

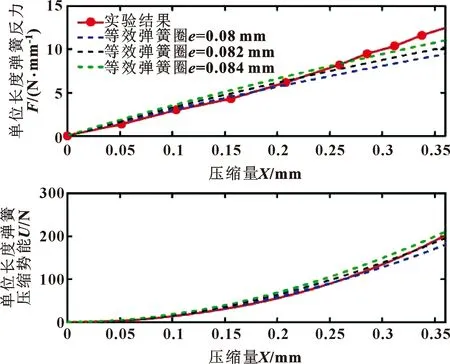
图3 螺旋弹簧与等效弹簧圈的反力以及弹性势能对比

使用等效弹性圈代替双螺旋弹簧圈后，泛塞封模型可以全部使用轴对称单元离散。由于夹套材料为近似不可压材料，因此需要使用杂交轴对称单元CAX4RH；为节省计算成本，等效弹簧圈与其他金属部件可以选用CAX4R单元进行离散[10]。泛塞封的夹套材料选用摩擦因数较低的聚四氟乙烯(PTFE)，其材料参数随温度变化较大[2]，如表2所示。运动轴、壳体以及等效弹簧圈的材料都设置为不锈钢[17]。

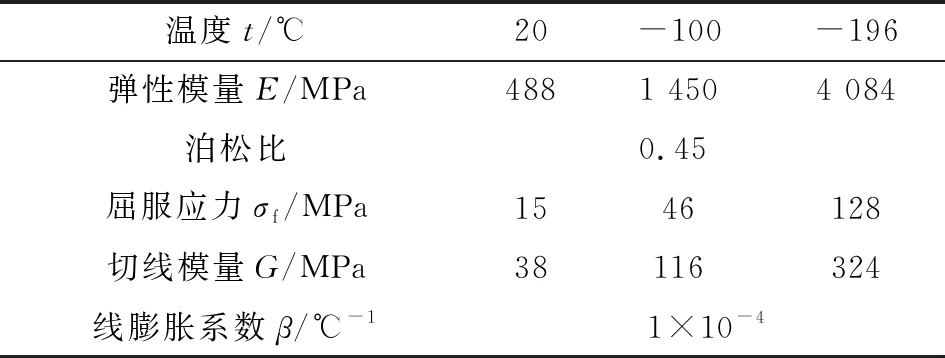
表2 不同温度下泛塞封夹套材料参数

模型中所有接触对都设置为面面接触，根据试验结果夹套外表面的摩擦因数为0.04，内表面与等效弹簧的摩擦因数设置为0.2[17]。

1.3 摩擦与密封性能模拟过程

利用有限元方法对弹簧密封圈摩擦与密封性能的分析过程一般可以分为3个阶段：第一阶段为常温装配安装过程；第二阶段为将模型从常温到低温的冷却过程；第三阶段在夹套的非接触部分施加介质压力，同时给轴恒定速度滑动并分析动密封过程中的摩擦与密封特性。

常温装配安装一般有2种方式。第一种方式[9]如图4(a)所示，对往复式轴和密封槽进行约束，对弹簧密封圈施加向下的位移，实现装配以及预压缩。该方式密封唇口受摩擦与挤压的共同作用，更接近真实的安装情景；劣势在于模型不宜收敛，尤其当夹套的过盈量比较大时，往往需要设置多段载荷步使其收敛，耗时较长。

第二种方式[12,14]是在初始建模时扩大安装槽的宽度，释放初始的过盈量，分别对轴与壳体施加向密封圈方向的位移载荷，如图4(b) 所示。这种安装方式与真实安装过程不同，且由于模型采用轴对称单元，径向的安装位移载荷会导致轴与壳中残留较大的预应力，因此在后续模拟中必须对轴与壳保持横向的位移约束；其优势在于模型易收敛，计算效率高。由于安装槽为金属材料，密封圈主要为非金属材料，且文中主要关注密封圈的性能，故忽略安装槽的变形情况。

图4 2种安装方式模型示意

图5、图6分别示出了2种安装方式装配泛塞封后夹套的Mises应力分布和塑性应变分布。对比使用以上2种方式装配泛塞封后夹套内的Mises应力以及等效塑性应变如表3所示。

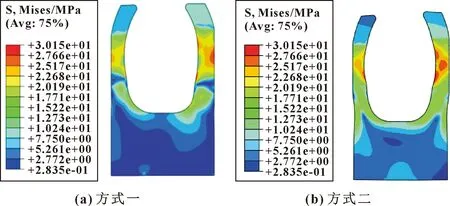
图5 2种安装方式装配泛塞封后夹套的Mises应力分布

图6 2种安装方式装配泛塞封后夹套的塑性应变分布

表3 不同安装方式下计算结果对比

产生塑性应变差异主要原因是，安装方式二弹簧的压缩量更小，且夹套唇部的纵向延伸量更大。安装方式一中泛塞封向下滑动时约束了夹套的纵向位移，在滑移到指定位置解除位移约束后，此时虽然夹套会进行纵向的延展变形，不过由于位移约束解除而产生的“载荷”是瞬时的、局部的，夹套来不及充分变形，只能增大局部的塑性应变；而在安装方式二中安装槽两侧准静态压缩泛塞封，可以使其充分变形，故塑性应变较小。

从计算需求及表3可知，安装方式二有较明显优势，故文中计算部分均采用安装方式二进行分析。

2 密封性能与摩擦性能分析

2.1 常温性能分析

图7示出了常温下在介质压力分别为5.0与13.0 MPa时泛塞封夹套表面的接触压力分布。由于模拟使用的泛塞封模型是外唇比内唇厚度大0.1 mm的非对称结构，因此在常温下外唇的接触压力与接触面积相比内唇更大,最大接触压力点出现在夹套过盈量最大的位置。随着介质压力增大，夹套与外壁的接触更加充分。

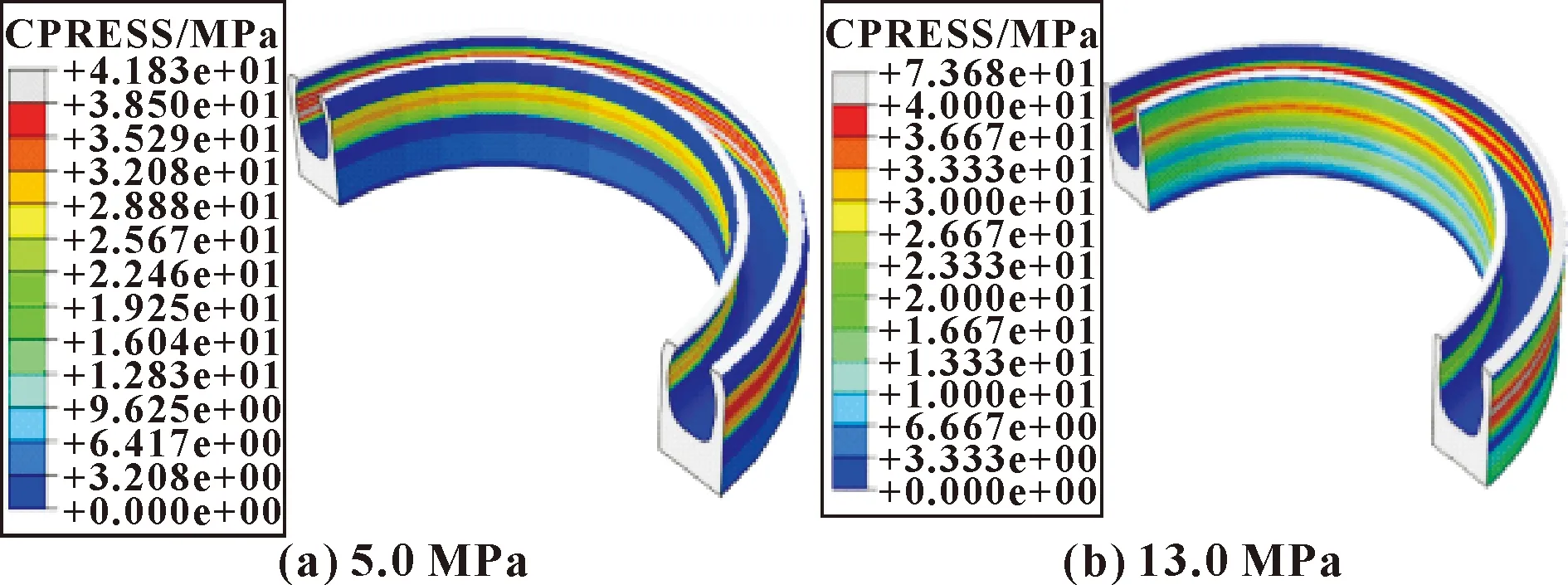
图7 常温下夹套表面接触压力

内外唇表面的接触压力随着介质压力变化情况如图8所示。可见，外唇的接触压力大小比内唇的更高，其峰值最大的位置近似一致。不过介质压力的提升会显著增加接触压力与接触面积。

图8 常温下夹套内、外唇在不同压力下的接触压力

此外，底座在轴向受压下径向会发生扩张，导致底座与壁面的接触面积与压力也将逐渐增大。当介质压力增大到16.0 MPa以上时，内、外唇部几乎都与外壁发生了充分的接触。由于该模型中内唇口为滑动接触面，文中重点分析常温下的泛塞封内唇的接触情况。如图9(a)所示，随着压力的增大，夹套内唇与轴之间的最大接触压力与接触面积都逐渐增大。在介质压力较小时，接触面积随压力增大变化很快，在介质压力增大至10 MPa时，夹套内唇几乎全部与轴发生接触，此时介质压力再升高，接触面积几乎不发生变化。

如图9(a)所示，最大接触压力的变化呈“S”型，当介质压力处于7～13 MPa之间时，最大接触压力变化比较缓慢，因为在这段压力区间夹套发生较大塑性变形，接触面积显著增大，介质压力对壁面的压力作用被分散；而越过这段压力区间，夹套与外壁的接触已经非常充分后，最大接触压力又随介质压力的增加快速变化。在整个压力范围内，最大接触压力值始终显著大于介质压力，因此可以判断其密封性能较好。测量不同压力下轴与夹套内唇口之间的摩擦力，以1 m/s的速度滑动轴，得到摩擦力结果如图9(b)所示。可见在分析范围内，摩擦力随介质压力的升高近似成正比。

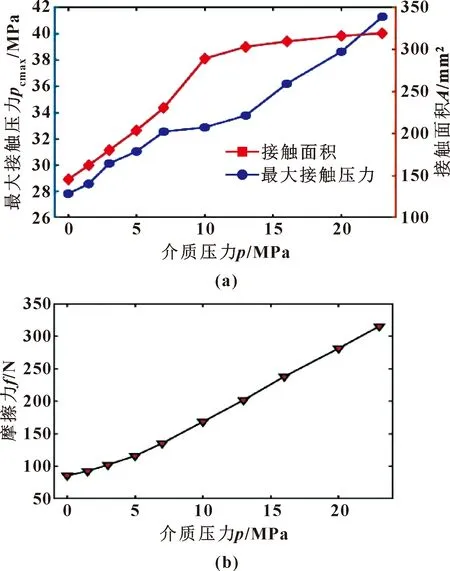
图9 常温下内唇最大接触压力、接触面积(a)以及摩擦力(b)随压力变化

2.2 低温性能分析

分析弹簧蓄能密封圈在低温下(-196 ℃)的动密封性能前，首先观察与分析泛塞封系统从常温降低至低温过程中体积收缩对密封接触状态的影响。

图10(a)显示的是降温至-196 ℃时泛塞封的收缩变形状态,可以观察到夹套整体的收缩变形与体积的明显减小。由于夹套为轴对称结构，因此其外侧的收缩变形显著大于内侧，其外侧与壳体的接触面积相比内侧的减小更为显著。不同低温环境下的内唇接触压力分布如图10(b)所示，随着温度的下降夹套收缩，内唇与轴的接触面积略有减小。此外，最大接触压力显著增大且峰值位置从弹簧接触区的中心位置移动到两端。这是由于夹套唇部在降温过程中不但有横向的收缩，也有纵向的收缩，夹套接触区域上方材料的纵向收缩导致材料在最大压缩位置上侧形成更大的富集与挤压，因此在初始接触区域的两侧出现较高的接触压力。而接触区域的材料会产生径向的收缩，使降温过程中接触区域中心位置的接触压力有一定程度的降低。

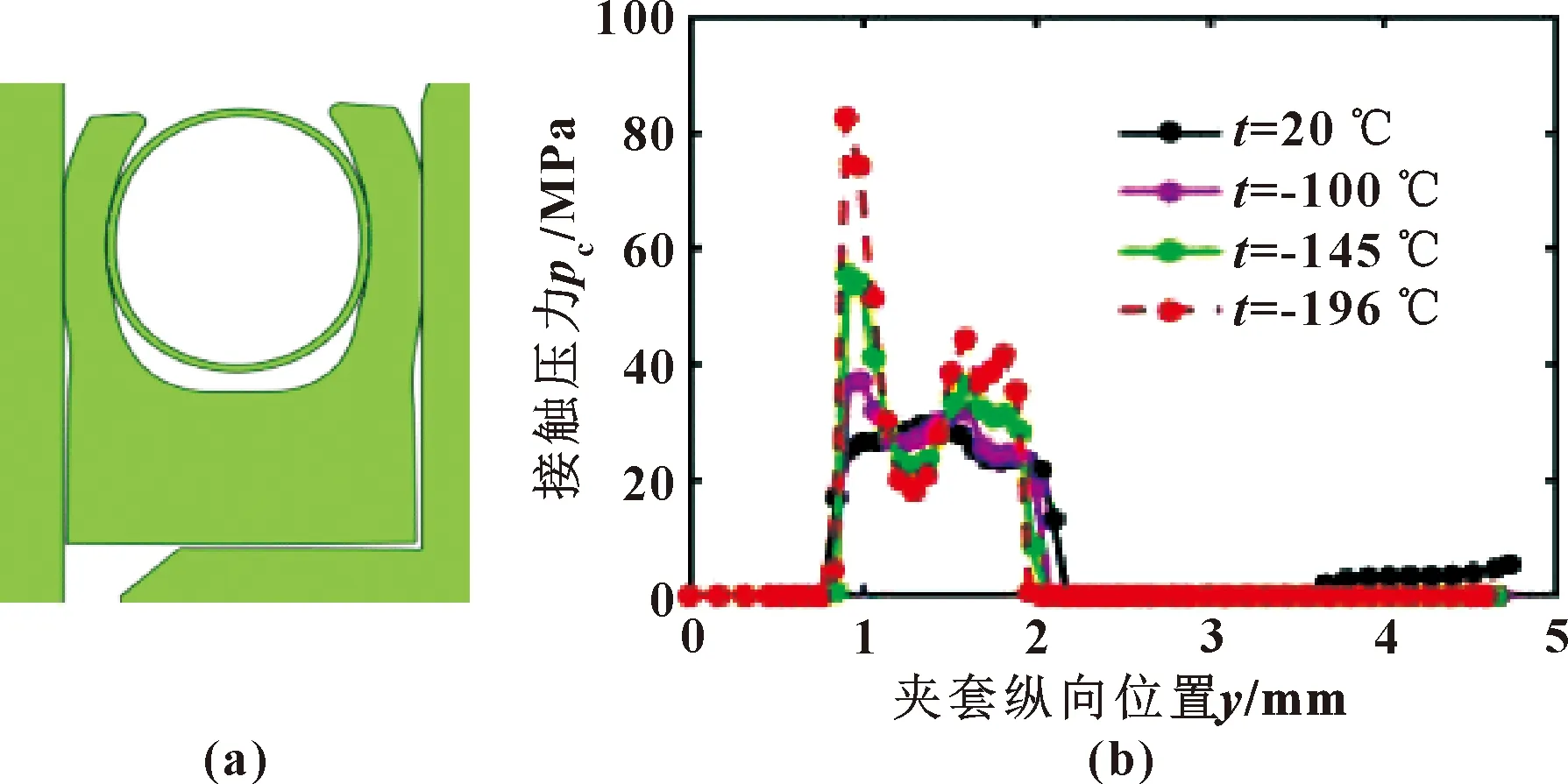
图10 无介质压力下降温至-196 ℃泛塞封的收缩变形状态(a)以及不同温度下夹套表面接触压力分布(b)

图11示出了-196 ℃下在不同介质压力下夹套内外唇的接触压力分布。不同于常温下的结果，低温下由于夹套的收缩导致内唇的接触压力与接触面积都比外唇更大。随着介质压力的升高，夹套的接触压力，尤其是接触区域两端的峰值将出现显著的升高。由于低温下夹套材料的刚度变大，因此随压力的增大，夹套的接触面积虽略有增大，但变化并不显著。低温下泛塞封内侧的密封性能好于外侧，因此对于低温下的泛塞封，需要关注外唇的接触情况。

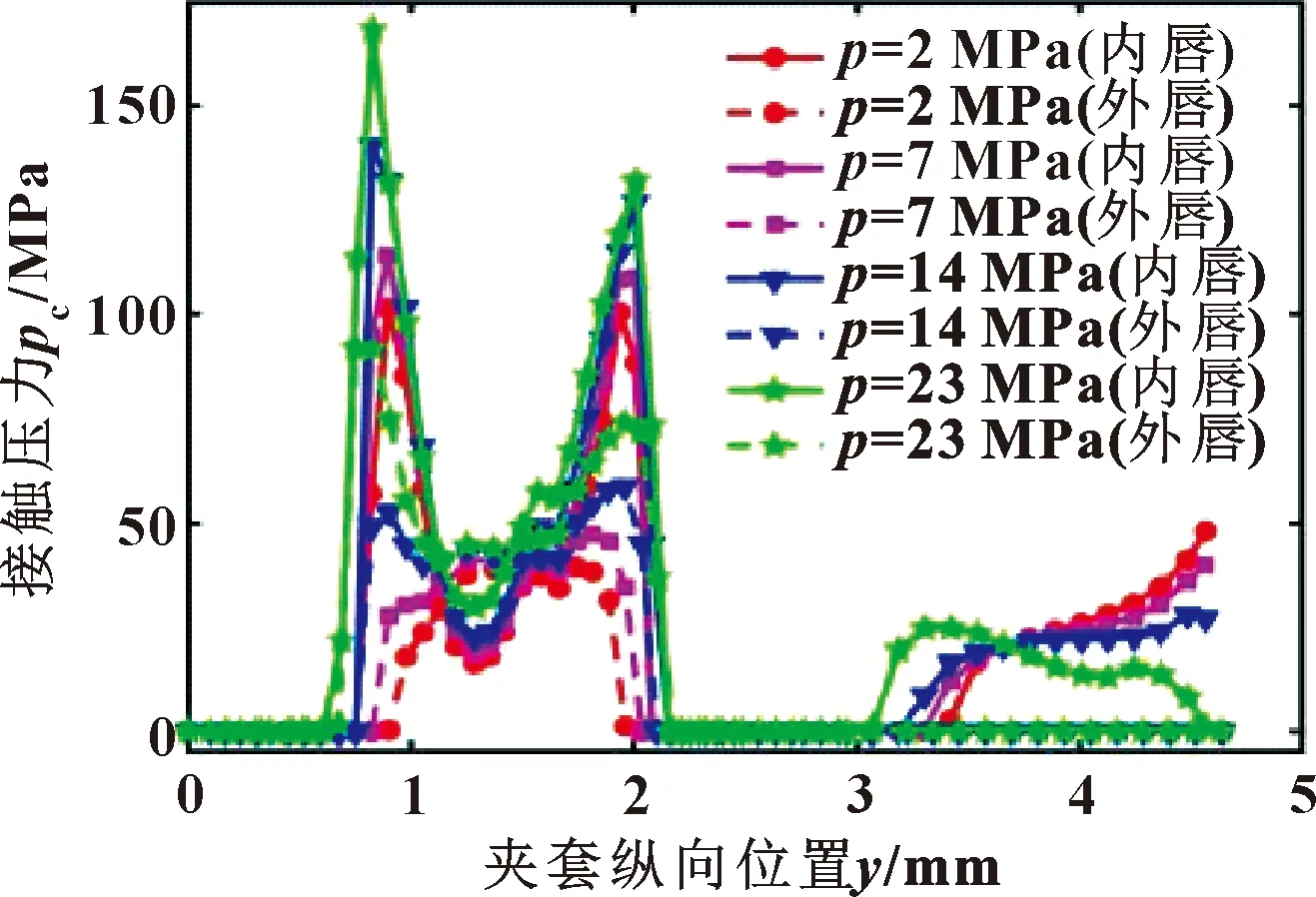
图11 -196 ℃下内外唇在不同介质压力下的接触压力分布

图12示出了-196 ℃下外唇接触压力、接触面积及-196和20 ℃下摩擦力随压力变化。由图12(a)可见，泛塞封外唇的最大接触压力与面积都随着介质压力增大而增大。不过对比常温下的结果，低温下由于夹套的刚度较大，增大的压力并没有显著增大夹套与外壁的接触面积。如图12(b)所示，低温下的摩擦力明显大于常温下的结果，随着压力的增大，低温与常温下的结果差别逐渐变小。在低介质压力下，低温环境中轴动摩擦力约是常温中的3倍，而在23 MPa的高介质压力下，这个比例降低至约1.1倍。这同样是由于低温下夹套材料刚度较大，介质压力的增大不会显著增大泛塞封与轴表面的接触，因此摩擦力的增长显著。

图12 -196 ℃下外唇接触压力、接触面积(a)及-196和20 ℃下摩擦力(b)随压力变化

泛塞封中的非金属夹套的剪切破坏是其失效的最主要形式[12]。图13展示了在低温环境中介质压力分别为4.0与18.0 MPa时轴滑动过程中夹套内部的剪应力分布。最大剪应力同样随介质压力的增加而变大,最大的剪应力出现在夹套唇的根部，尤其在内唇的根部位置。左右2个唇根部的剪应力方向相反，这主要是由于底座的降温收缩以及唇部受压方向不同所致。试验结果也显示，泛塞封的破损与失效也常常发生在内唇根部位置。

图13 超低温-196 ℃下不同介质压力下的剪应力分布

3 弹簧蓄能密封圈结构优化及性能分析

针对泛塞封的几何形状进行优化设计，目标是在尽可能保障接触压力与接触面积的前提下，减小轴滑动时的摩擦力，以减小泛塞封的磨损以及工作状态下的阻力。尽管常温与低温下泛塞封的密封与摩擦性能的变化趋势类似，不过最大摩擦位置有明显不同。在液体火箭发动机阀门系统中，更关注泛塞封在低温下的性能，因此下面将主要针对泛塞封在低温工况环境的性能进行结构优化分析。

3.1 增加内唇外侧表面突起

根据前文的模拟结果，低温环境下内唇的接触面积与接触压力都大于外唇，即内唇的密封相比外唇有更大的余量。此外，泛塞封的动密封摩擦力也是由于内唇表面产生的。

基于以上两点考虑，改进内唇结构,减小内唇与轴的接触面积，从而减小滑动摩擦力。保证过盈量不变，在内唇外侧减薄0.1 mm，并在弹簧接触位置设置0.1 mm的凸起，如图14(a)所示。图14(b)(c)展示了内唇修改后泛塞封在安装与降温下几何变形。对比原始泛塞封(见图10(a))，内唇与轴的接触面积减小约35.0%。

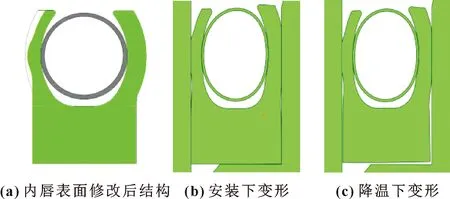
图14 内唇表面修改后结构及不同工况下的几何变形

图15对比了内唇优化模型与初始模型的内唇表面接触压力分布。在弹簧压力区域的接触压力同样呈现两端峰值，中间较小的现象，且优化模型最大接触压力与初始模型的结果差别不大。但由于内唇表面的突起，使得内唇口与轴间的接触面积显著减小，且接触面积几乎不随介质压力的增大而增大。密封圈对轴的抱紧力可以定义为

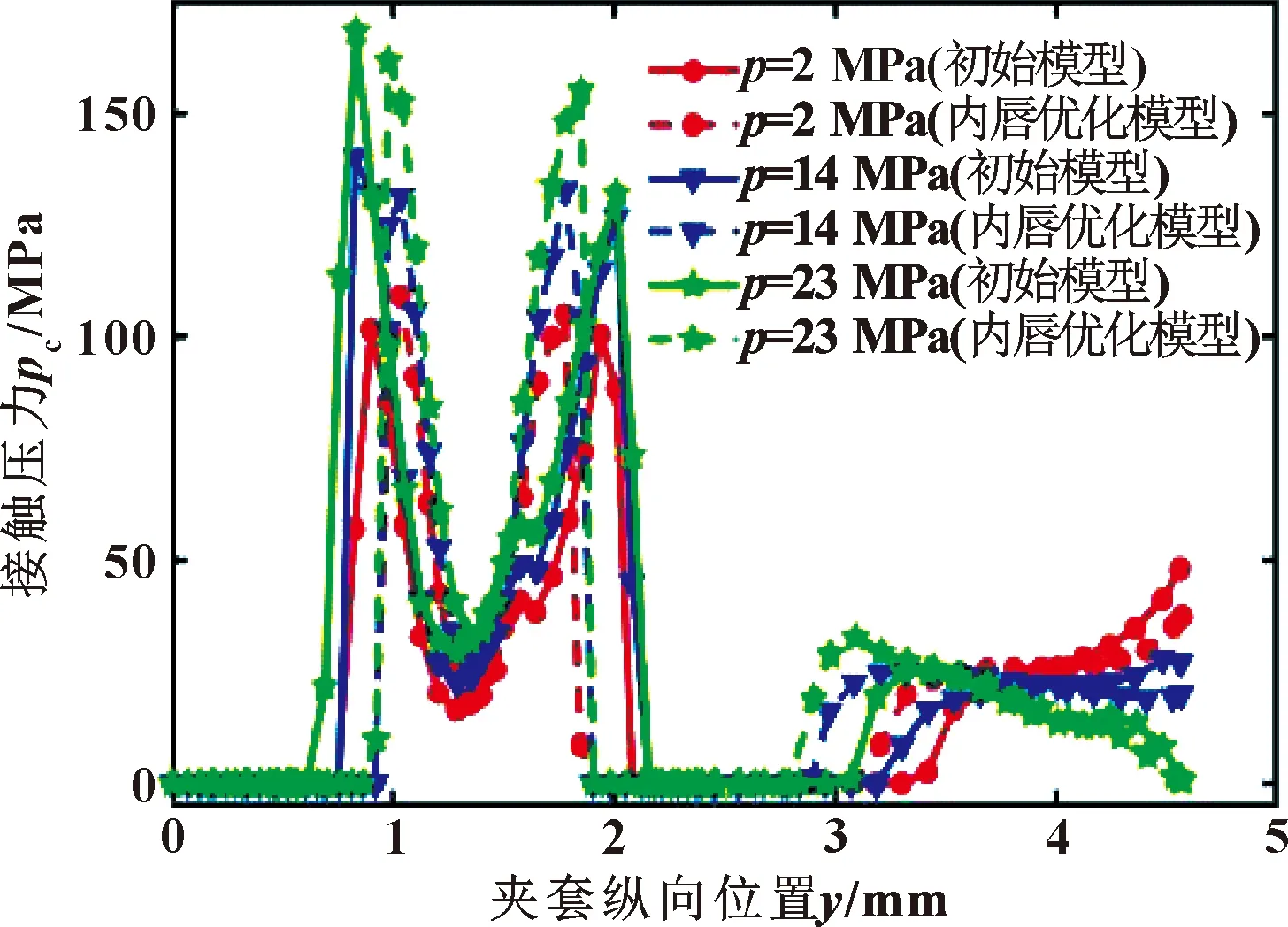
图15 不同压力下初始模型与内唇优化模型的内唇接触压力分布

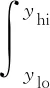
(1)

式中:R代表滑动轴的半径;ylo与yhi分别代表夹套接触区域纵向位置的坐标;pc为接触压力。

由于改进模型接触区域较小，在pc变化不大的前提下，改进密封圈对轴的抱紧力也将减小。由库仑摩擦模型预测，摩擦力也将有所减小。

对比内唇优化模型与初始模型在不同介质压力下的摩擦力，如图16所示。可以观察到优化模型摩擦力有所减小，其中在稳定工作介质压力23 MPa的环境下摩擦力降低约10%。不同压力下校核改进模型中的剪切应力分布，如图17所示。

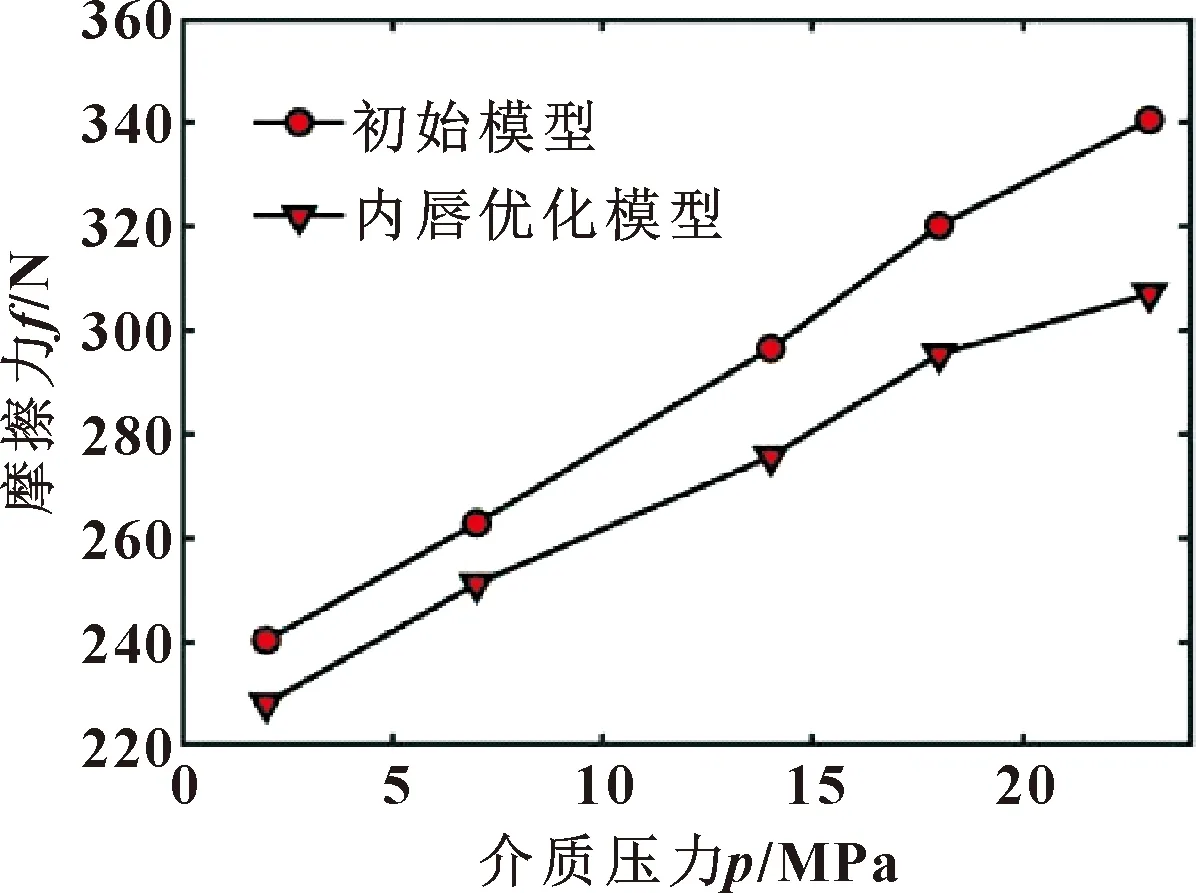
图16 不同压力下初始模型与内唇优化模型的摩擦力分布

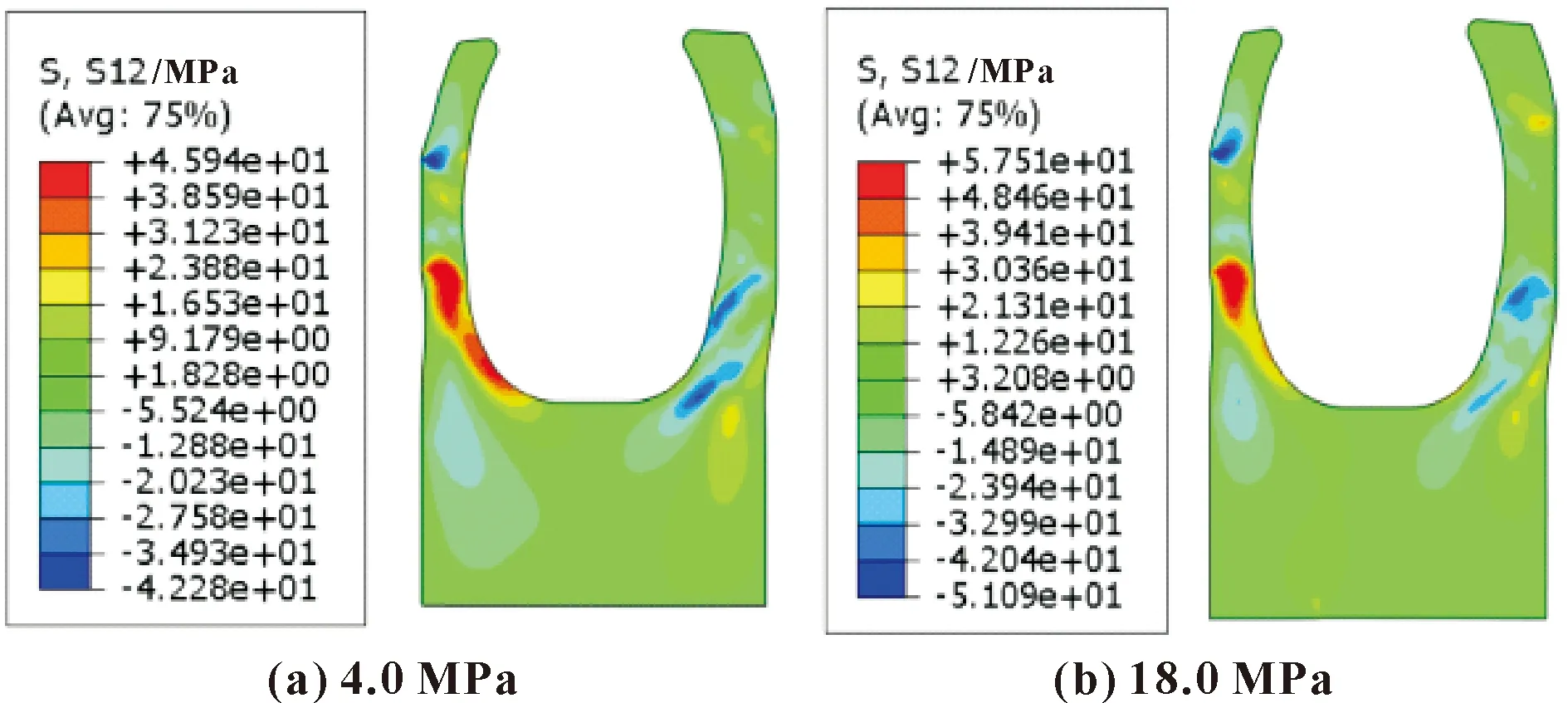
图17 低温下不同介质压力下内唇优化模型的剪应力分布

对比图13和图17可以看出，相比4.0和18.0 MPa 2种介质压力下初始模型的最大剪切应力值，内唇改进模型的最大剪切应力值分别增大了11.4%、8.9%，这是由于内唇中间位置的突起导致介质压力下根部的剪切变形更大。综上，这种对内唇的优化方案可以在一定程度降低摩擦力，不过也会一定程度上降低夹套工作中的抗破坏能力。

3.2 减小底座宽度

如图18所示，在降温收缩以及介质压力的作用下，底座也会与轴发生接触。由于底座与轴之间的接触压力水平相比唇部小很多，因此对密封性能的提高影响不大。因此考虑在靠近轴的内侧减小底座的宽度以避免底座与轴之间的接触摩擦。如图18(a)所示为将底座宽度减小0.1 mm的模型示意图。图18(b)(c)分别为改进模型安装以及降温后的几何变形，在这个过程中夹套底座与轴始终未发生接触。

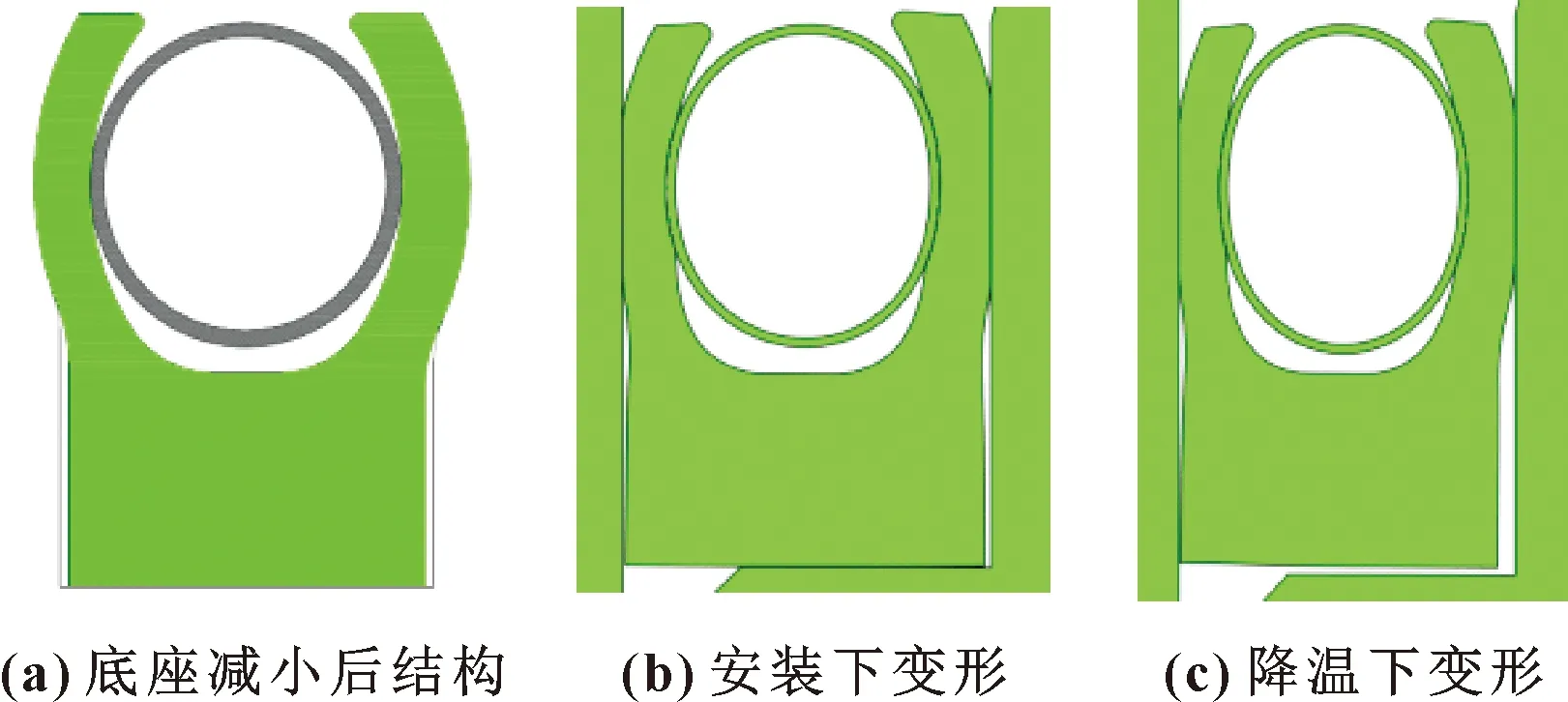
图18 减小底座后结构及不同工况下的几何变形

对比减小底座宽度模型与初始模型在不同介质压力下内侧的接触压力分布，如图19所示。唇部的接触压力近似没有变化，不过底座与轴之间几乎不再有接触压力。

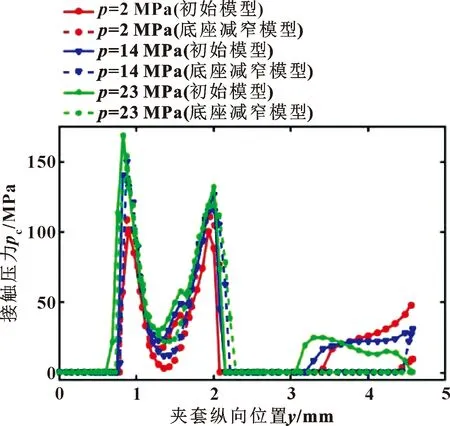
图19 不同介质压力下初始模型与底座减窄优化模型的内唇接触压力分布

计算并对比减小底座模型与初始模型在不同介质压力下的摩擦力，如图20所示。减小模型底座宽度对降低摩擦有着很好的效果，同样对比在23 MPa工作环境下的摩擦力大小，改进模型可以将摩擦力降低18.7%。不过底座宽度减小会降低底座对上端唇部的支撑作用，从而导致在介质压力作用下的唇根部的剪切应力增大。如图21所示，剪切应力的最大值在4.0与18.0 MPa的工作环境下分别有30.7%与10.1%的增加。综上，尽管减小底座宽度对降低轴动摩擦有很好的效果，不过这种优化方式同样会在一定程度上导致泛塞圈的剪应力增大。

图20 不同介质压力下初始模型与底座减窄优化模型的摩擦力分布

图21 低温下不同介质压力下底座减窄优化模型的剪应力分布

3.3 减小蓄能弹簧刚度

如图11所示，夹套与外壁的接触压力值都显著大于介质压力，有较大的过盈量；且夹套受到蓄能的弹簧的挤压变形过大，塑性应变的最大值在0.3以上。因此计划通过降低蓄能弹簧圈的刚度减小蓄能圈对唇部的挤压与支撑。数值模型中通过直接减小弹簧圈的刚度实现对蓄能弹簧圈支撑刚度的减弱，如图22所示，将刚度减小约40%。在实际使用中可以通过减小弹簧圈匝数、厚度等方式同样实现对蓄能弹簧圈支撑刚度的减弱。

图22 蓄能弹簧反力曲线试验结果对比

在低温下泛塞封的外唇与壁面的接触是密封性能的薄弱环节，图23对比了弹簧密封圈刚度减弱的模型与初始模型外唇的接触压力曲线。弹簧刚度降低模型的最大接触压力与接触面积相比初始模型有一定降低，不过降低幅度并不显著。可见该模型改进方案对密封性能的影响并不显著。

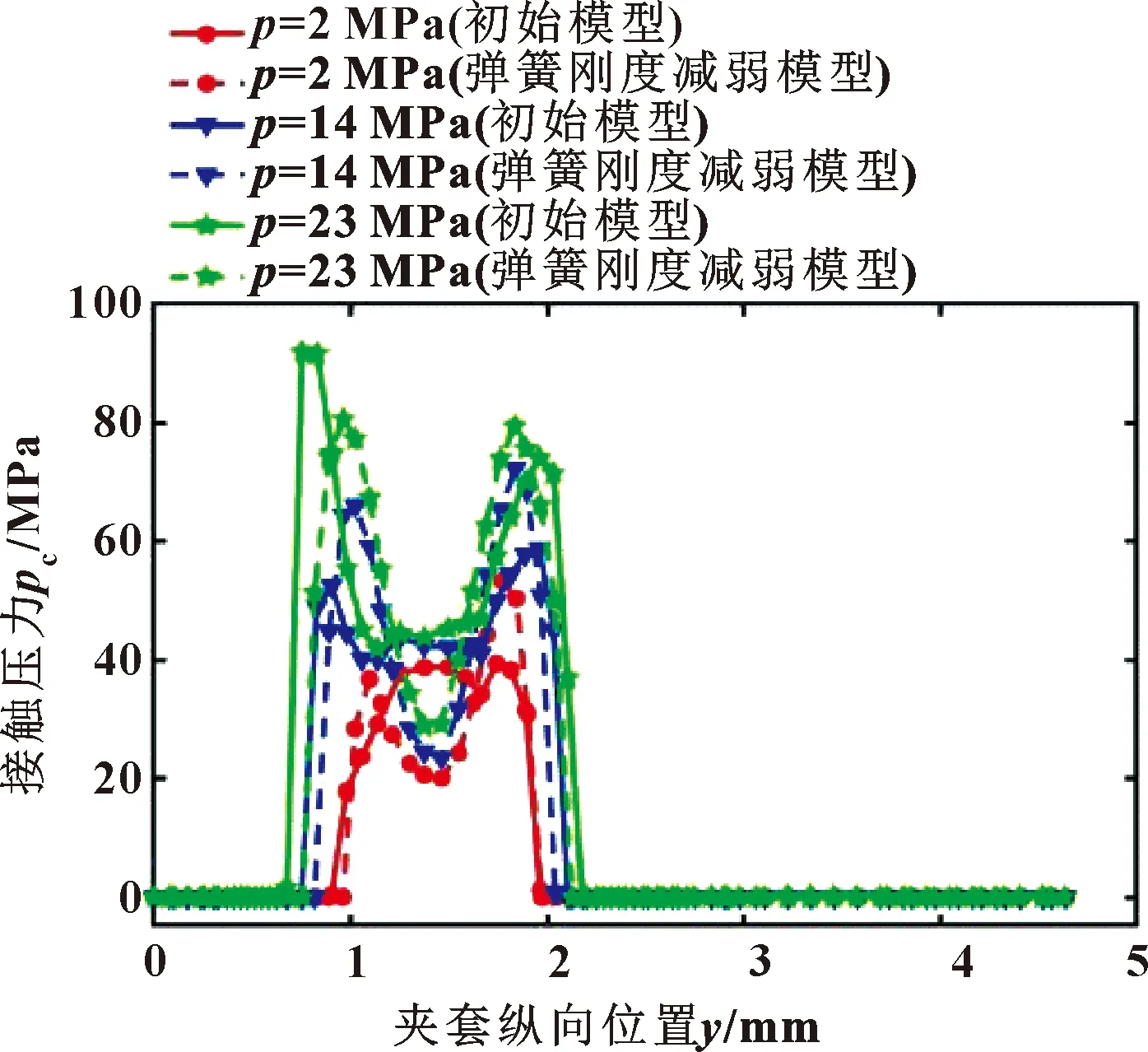
图23 不同介质压力下初始模型与弹簧刚度减弱模型的外唇接触压力分布

弹簧刚度减弱对摩擦力降低的效果非常明显。如图24所示，相比前2种结构优化方案，减弱弹簧刚度对摩擦力的降低更为显著。其中在23 MPa介质压力下摩擦力降低约32.6%。在原始模型中，夹套过盈对轴抱紧力的贡献显著小于弹簧圈反力的贡献，因此降低弹簧圈的刚度可以明显降低滑动摩擦力。

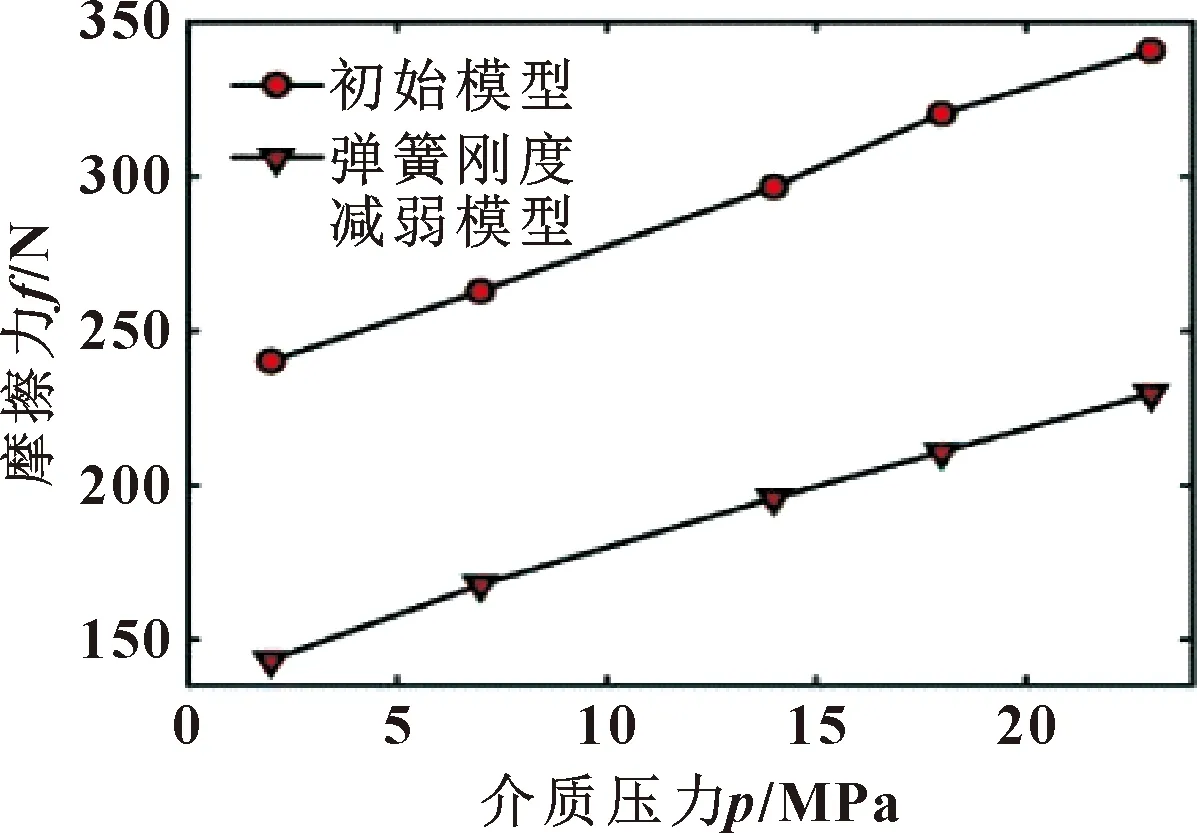
图24 不同介质压力下初始模型与弹簧刚度减弱模型摩擦力分布

此外，进一步考虑该优化模型对泛塞封强度的影响，如图25所示，在介质压力4.0与18.0 MPa下，夹套内的剪应力最大值分别降低了26.3%与26.8%。

图25 低温下不同介质压力下弹簧刚度减弱模型的剪应力分布

4 结论

(1)采用等效刚度方式构建轴对称等效弹簧圈模型代替双螺旋蓄能弹簧，并对比分析了泛塞封的2种安装模型，使用该二维轴对称模型计算的常温零压下的摩擦力与试验值吻合良好。

(2)常温下泛塞封外唇的接触压力与接触面积相比内唇更大，低温下泛塞封内唇的接触压力与接触面积相比外唇更大。常温下随着介质压力增大，接触压力与接触面积都发生增大，但变化趋势不同。对于接触面积，当介质压力大于一定值后几乎不再增长；对于接触压力，在夹套与外壁接触充分后，还将随介质压力增长而显著增大。低温下外唇的接触压力与接触面积都随介质压力的升高而增大，不过接触面积的变化较小。

(3)常温下及低温下内唇与轴的摩擦力随压力增大呈近似线性增长。不过介质压力从3 MPa至23 MPa的变化过程中，低温下的摩擦力与常温下的摩擦力之比从3倍降低至1.1倍。

(4)内唇口外侧表面凸起、减薄底座尺寸2种优化方案可以降低摩擦力，但是却伴随着夹套破坏强度的降低；而降低弹簧圈的刚度不但可以降低摩擦，也可以在一定程度上提升密封圈抗破坏的能力与使用寿命。