斯特林机动力活塞间隙密封动态特性仿真分析*

宫 晶 张君安 王亚娟,2 卢志伟 刘 波

(1.西安工业大学机电工程学院 陕西西安 710021；2.陕西能源职业技术学院煤炭与化工产业学院 陕西咸阳 712000 )

间隙密封作为自由活塞斯特林机中的一项关键技术,是利用密封零件之间的径向微小间隙及该间隙在轴向的一定长度来实现的一种密封形式。该间隙可以在完成密封作用的同时消除接触磨损和产生的污染[1]。但是由于有间隙存在，当间隙两端的压力不相等或活塞存在运动时就会造成间隙内气体的泄漏，影响斯特林机的整机性能、工作寿命以及可靠性[1]。

陈曦等人[2]推导了活塞运动时环形间隙的泄漏量和一个周期内的平均泄漏量的计算公式，并分析了其对直线压缩机的影响以及偏心对间隙密封的影响。马诗旻等[3]基于压力波和活塞位移波的简谐变化规律，建立了斯特林机间隙密封的数值模型，模拟了间隙内氦气在不同工况下的层流流动。李廷宇等[4]对冰箱直线压缩机的间隙密封进行了数值模拟，分析了在不同制冷工质条件下的泄漏特性。曹广亮等[5]分析了板弹簧组件对直线压缩机间隙密封泄漏特性的影响。刘贤贤等[6]利用Fluent软件进行了气体轴承与间隙密封耦合特性的数值模拟与分析，验证了其在自由活塞斯特林机中应用的可行性。徐安波等[7]对间隙密封的影响因素进行了权重分析，结果表明影响密封效果的3个显著因素为气膜厚度、压差和密封长度，其他因素无显著影响。MABROUK等[8]提出了一个非定常分析模型来计算气体泄漏质量流量，考虑了环形间隙中的振荡流，并评估了斯特林机功率损失的影响。SAUER和KÜHL[9]对气缸及间隙密封进行改进并进行了实验研究，分析了其对斯特林机的功率损失。王成刚等[10]利用FLUENT 软件建立了冲击气缸往复运动间隙密封的模型，并对密封性能进行了研究。BRAGA和DESCHAMPS[11]基于雷诺方程的可压缩流体流动模型预测了往复式压缩机的泄漏，评估了间隙几何形状和活塞速度对泄漏和压缩机效率的影响。SMIRNOV等[12]对无活塞环的10 μm高公差密封进行了实验研究，分析了通过密封间隙的气体泄漏率。QI等[13]通过分子动力学模拟研究了气体通过间隙密封泄漏的分子机制，结果表明泄漏率与压差和气膜厚度成正比。LOHN和 PEREIRA[14]使用三维计算流体动力学模型分析了诸如活塞和气缸之间的未对准和部件几何误差等因素对气体泄漏的分析。

综上所述，目前对斯特林机中间隙密封的研究主要集中于稳定后环形间隙周期内的平均泄漏量以及泄漏对功率损失的影响，对其动态特性的分析较少。本文作者从压缩循环过程的初始状态开始，到稳态结束，全程分析了不同形式密封对间隙密封泄漏量的影响，并分析了泄漏量的影响因素。

1 间隙密封的模型建立

首先对自由活塞斯特林机间隙密封动态特性分析的物理模型进行简化，如图1(a)所示，在完全密闭的气缸中，忽略工作腔中的配气活塞实体，按等温模型将压缩腔和膨胀腔体积之和作为工作腔的体积，活塞另一侧为背压腔，活塞在其间做往复运动，活塞与气缸间存在微小间隙，工作腔和背压腔内气体可以通过间隙进行交换。图1(b)所示为间隙处气体流动的物理模型。

图1中，气膜间隙厚度为h，活塞运动速度为U，位移为s，pc和pb分别为稳定后的工作腔压力和背压腔压力。

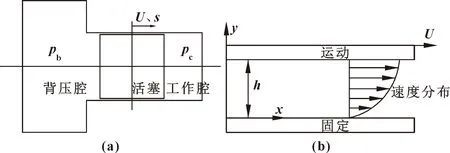
图1 间隙密封的物理模型

该物理模型的假设条件[15]如下：

(1) 气膜的厚度与宽度、长度相比很小。

(2) 间隙在往复相对运动过程中没有旋转运动，间隙内气体可看作一维流动。

(3) 沿气膜厚度方向上不计压力变化。

(4) 忽略质量力的影响。

(5) 内外圆柱面是同心的，因此间隙高度在圆周方向处处相等。

(6) 流体的惯性力与黏滞力相比可以忽略不计。

基于以上假设条件，利用动量方程和理想气体状态方程建立间隙密封的数学模型：

(1)

如图1所示，运动表面有向右的速度U，即y=h处气体速度为U，固体边界处气体速度为0，即y=0时气体速度为0，则边界条件为

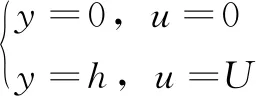
(2)

式中:u为气体速度;R为气体常数，与气体种类和温度有关;T为气体温度;μ为气体动力黏性系数。

对式(1)进行2次积分并代入边界条件，求解可得气体运动速度：

(3)

对式(3)在气膜厚度方向上积分，可得单位时间内通过单位宽度截面的体积流量：

(4)

对式(4)在宽度上积分，可以得到单位时间通过活塞周向一周的总的质量流量为

(5)

当活塞运动时，两侧工作腔和背压腔的压力及活塞速度是不断变化的，因此泄漏的流量也随着时间变化。在式(5)中，第一项为由速度引起的质量流量，第二项为由压差引起的质量流量。

2 3种间隙密封形式

由公式(5)可知，由压差引起的质量流量随密封长度L而变化。对于由压差引起的质量流量的变化，分为如图2—4所示3种情况考虑。

图2所示为密封长度不变的密封模型。活塞右侧为工作腔，左侧为背压腔，当活塞有向右的运动速度，速度方向为正时，密封长度不变，工作腔气体质量减少进入间隙，间隙内原来的气体进入背压腔，背压腔气体质量增加；当活塞向左运动时，工作腔气体质量增加，背压腔气体质量减少。

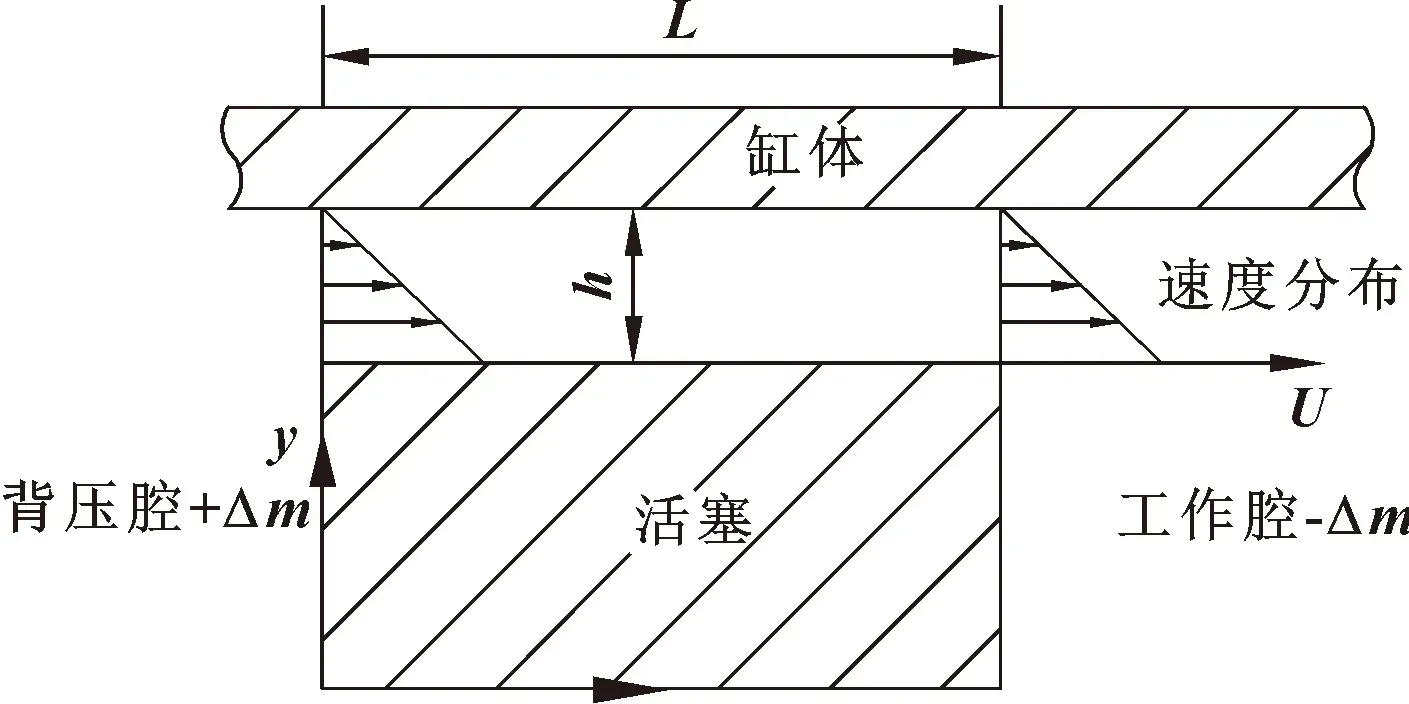
图2 间隙密封长度不变

图3所示为密封长度单侧变化的密封模型。当活塞向右运动，速度方向为正时，密封长度增加，两侧腔体内气体进入间隙，工作腔气体质量减少，背压腔气体质量减少；当活塞向左运动时，密封长度减少，工作腔气体质量增加，背压腔气体质量增加。

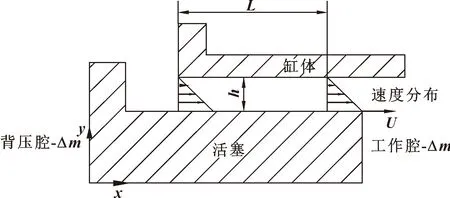
图3 间隙密封长度单侧变化

图4所示为密封长度双侧变化的密封模型。活塞向右运动，速度方向为正时，密封长度减小，工作腔气体质量增加，背压腔气体质量增加；当活塞向左运动时，密封长度先增加后减小，工作腔气体质量先减少后增加，背压腔气体质量先减少后增加。

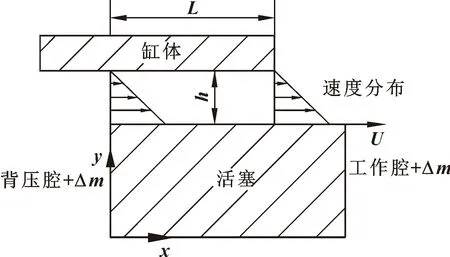
图4 间隙密封长度双侧变化

3 间隙密封动态特性的数值仿真

3.1 仿真流程

在求解两腔压力时，先对初始时刻，即零时刻的状态赋值，给定初始容积、压力、时间推进长度等数据，计算出一个Δt后各腔的压力和活塞的速度，由以上数据计算出由压差和速度引起泄漏的质量流量，从而得到Δt后各腔新的压力值。对这个过程反复循环，求出各腔压力及质量流量的动态特性。图5所示即为时间推进法求解间隙密封的动态特性的流程图。

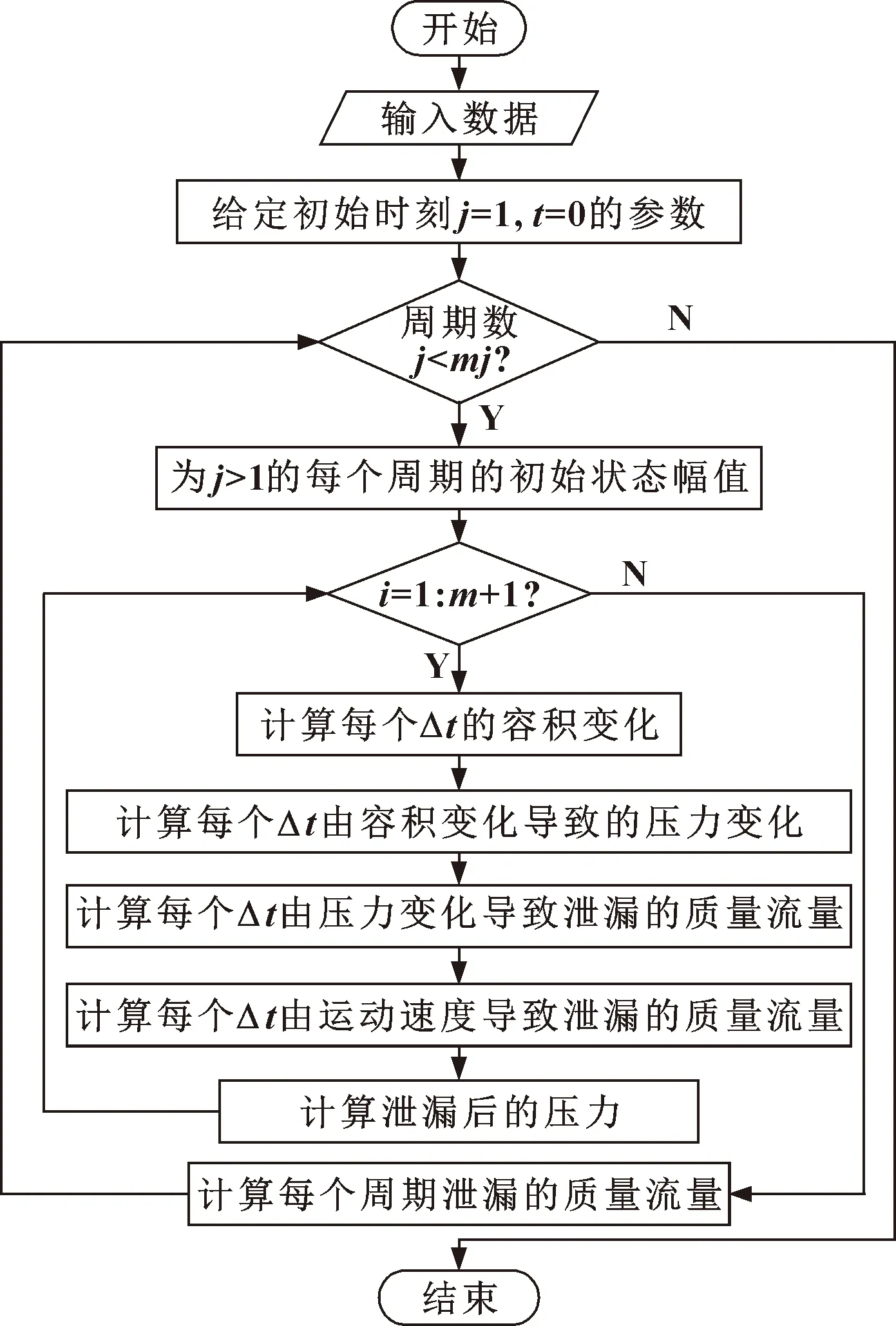
图5 程序流程

3.2 模型验证

为了验证文中仿真模型计算结果的正确性，比较了文献[3]通过Fluent层流模型对斯特林机间隙密封泄漏特性分析的计算结果，其中活塞半径为2 cm，活塞长度为7 cm，气膜厚度为20 μm，频率为60 Hz，活塞振幅为0.1 cm。图6示出了文中间隙密封计算结果和文献结果的趋势对比；同时取两者差值较大的两点进行误差对比分析，如表1所示。

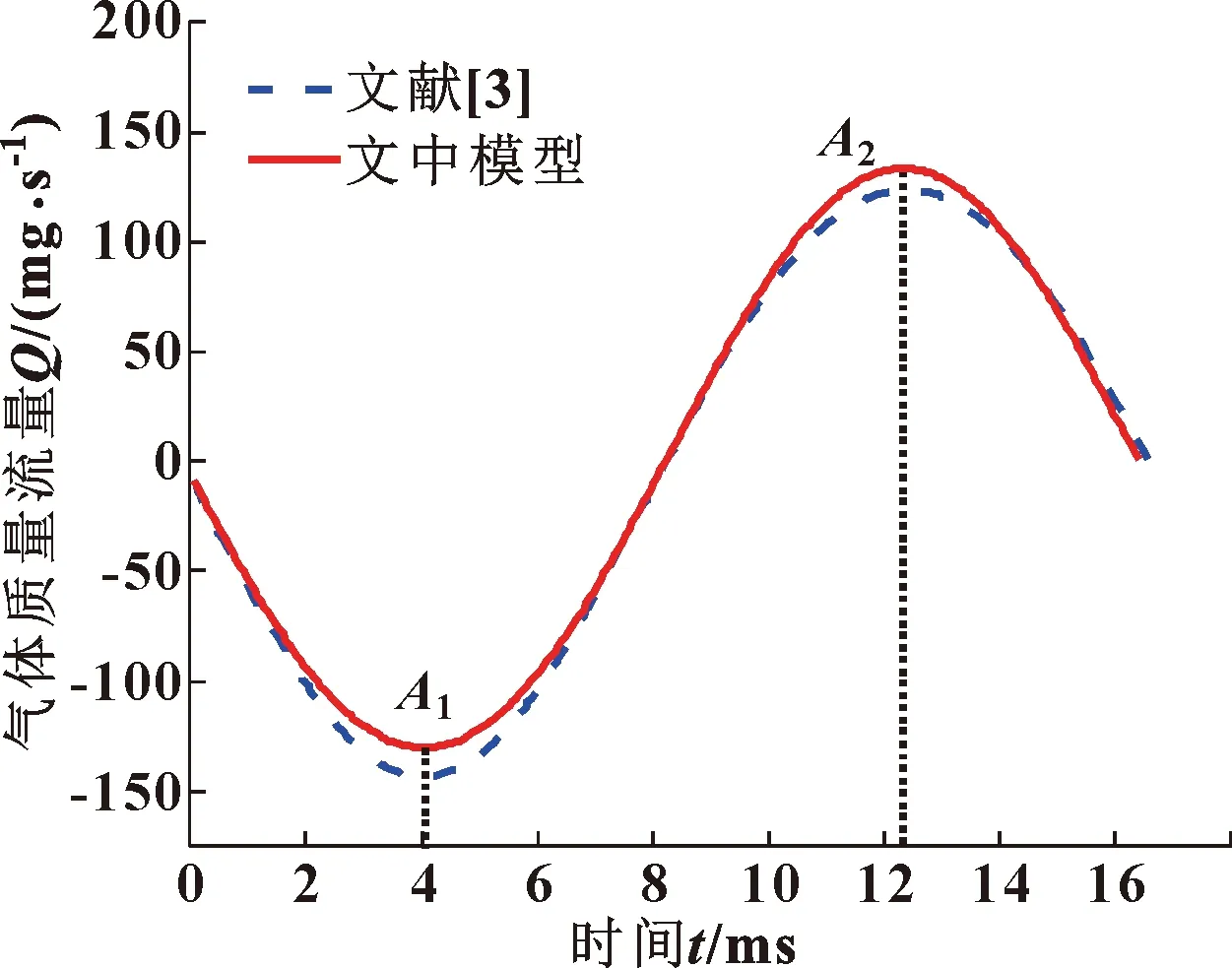
图6 间隙密封计算结果对比

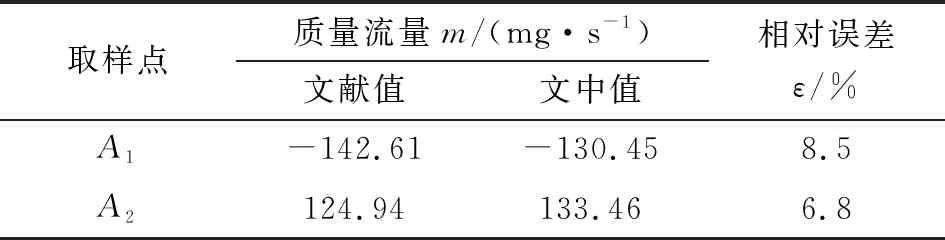
表1 质量流量计算结果误差对比

如图6和表1所示，两者泄漏的气体质量流量趋势一致，最大相对误差为8.5%，出现在点A1。由于部分计算参数和仿真方法存在一定差异，仿真结果较参考文献值也有一定误差，但总体在合理范围内。因此文中所建立的计算模型正确，计算结果有效。

4 间隙密封动态特性仿真分析

依据图5给出的求解方法，利用Matlab软件对3种密封模型进行仿真分析，计算模型相关参数如下：活塞半径R=2.5 cm，长度L=10 cm，间隙为h=30 μm，温度T=273 K，初始压力p0=0.3 MPa，频率30 Hz。

4.1 间隙密封长度不变

图7和图8所示为运行3个周期后的循环压力以及由压差引起的质量流量变化(Q1)和由速度引起的质量流量变化(Q2)。可知，压力和质量流量都呈周期性变化。

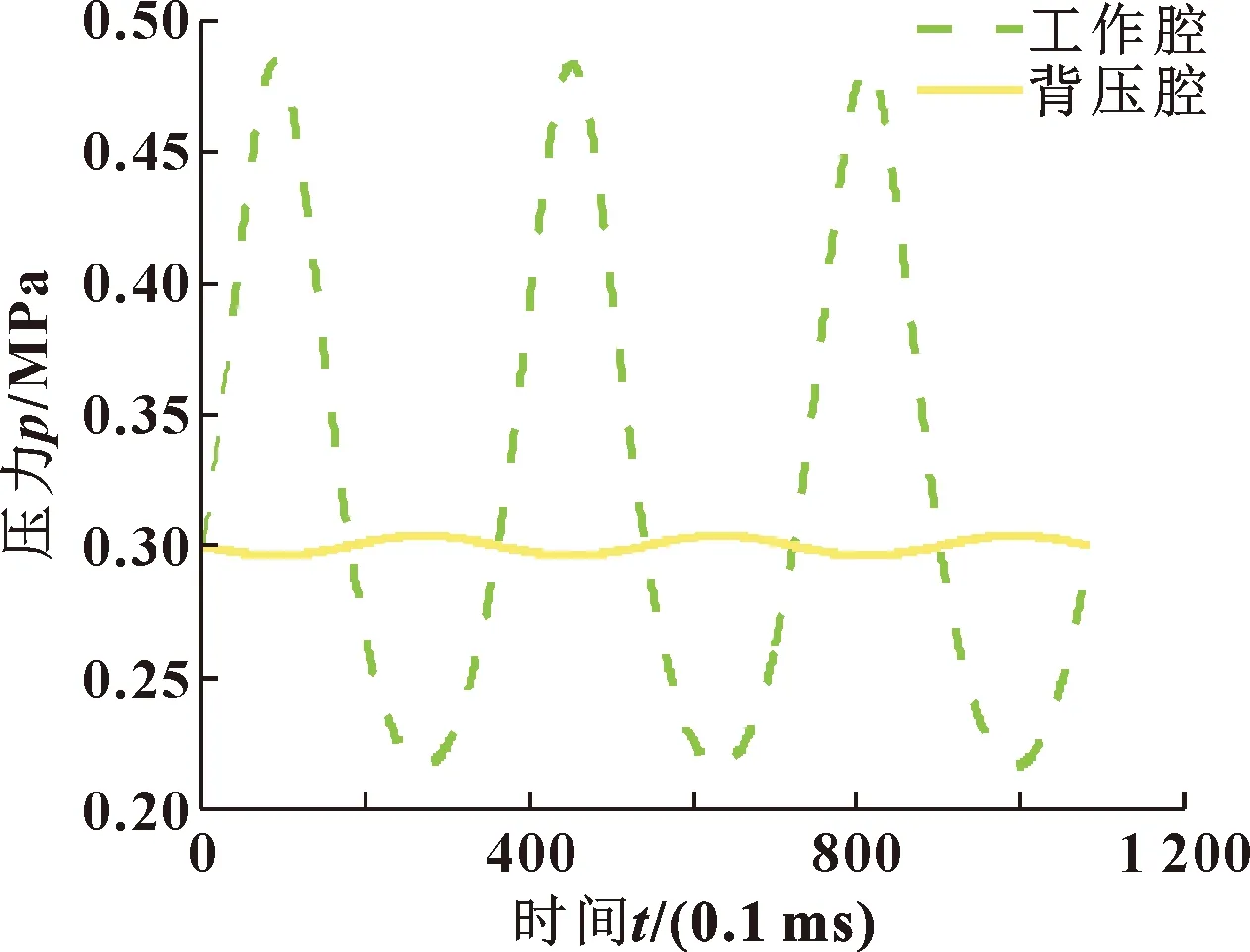
图7 间隙密封长度不变时工作腔(pc)和背压腔(pb)压力分布(3个周期)

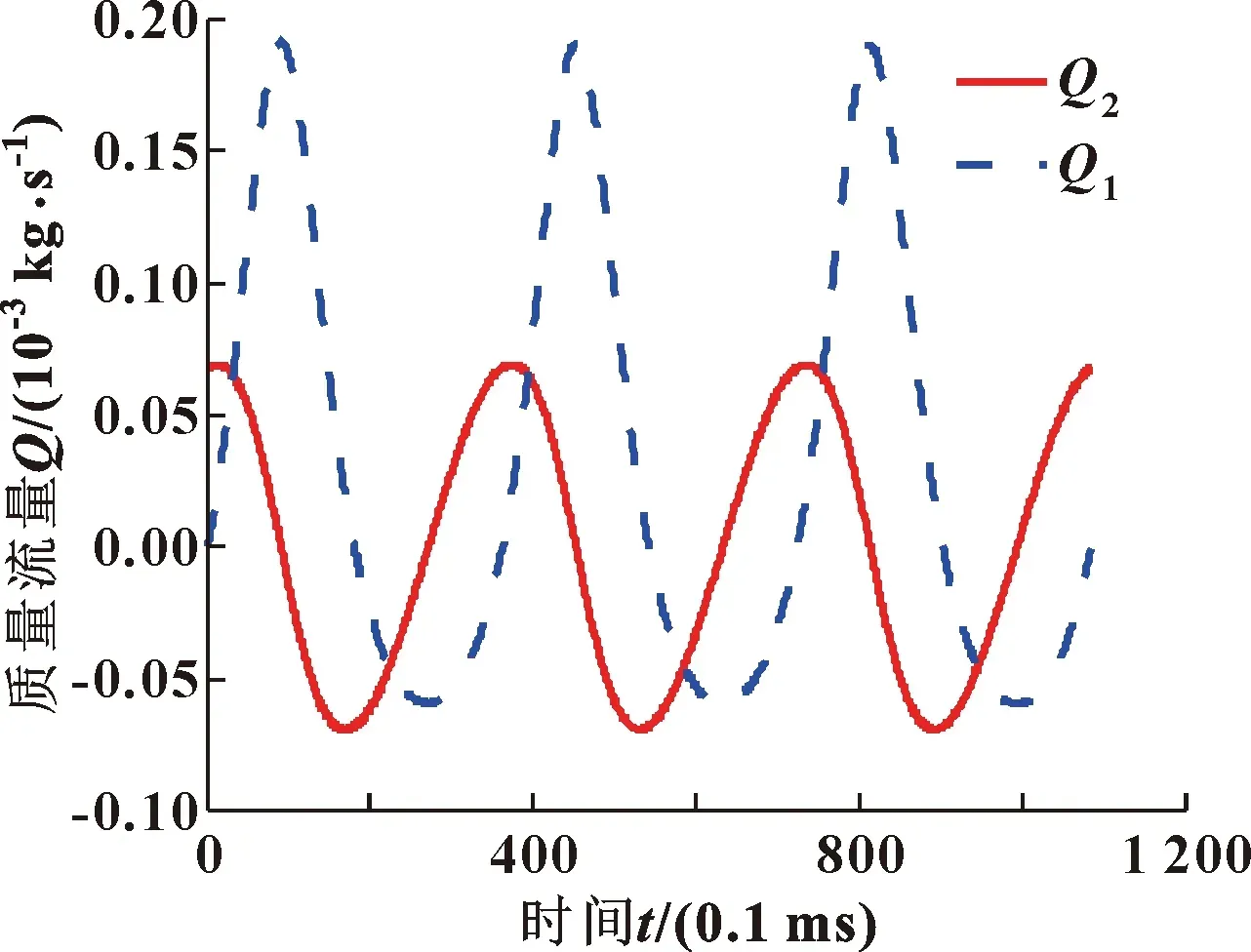
图8 间隙密封长度不变时质量流量变化分布(3个周期)

图9和图10所示为运行650个周期后的循环压力及由压差引起的质量流量变化(Q1)和由速度引起的质量流量变化(Q2)。

图9 间隙密封长度不变时工作腔(pc)和背压腔(pb)压力分布(650个周期)

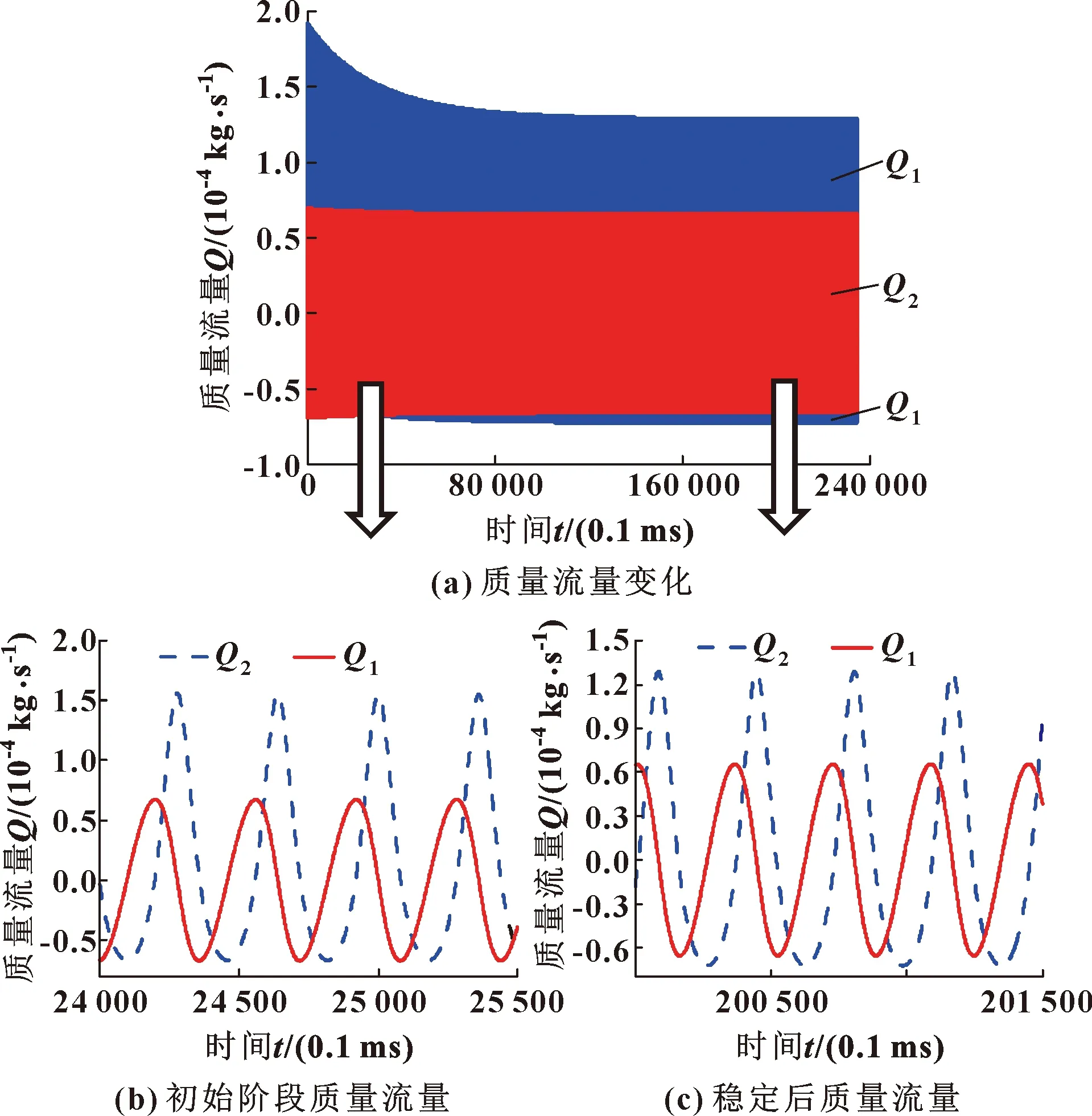
图10 间隙密封长度不变时质量流量变化分布(650个周期)

其中，图9(b)(c)及图10(b)(c)分别为在初始过程及稳定后的压力和质量流量细节。

由图9和图10可以看出，最初工作腔内压力较大，气体从工作腔向背压腔泄漏;随时间的增加，工作腔压力逐渐减小，背压腔压力几乎不变，可等同于初始压力;工作腔向背压腔泄漏的质量流量逐渐减少，背压腔向工作腔泄漏的质量流量逐渐增加;然后在某一时间，压力和质量流量都达到了平衡状态。

4.2 间隙密封长度单侧变化

图11与图12所示为运行650个周期后的循环压力以及由压差引起的质量流量变化(Q1)和由速度引起的质量流量变化(Q2)。图11(b)(c)及图12(b)(c)分别为在初始过程及稳定后的压力和质量流量细节。

由图11和图12可知，工作腔向背压腔泄漏的质量流量逐渐减少，背压腔向工作腔泄漏的质量流量逐渐增加，在某一时间，压力和质量流量都达到了平衡状态。

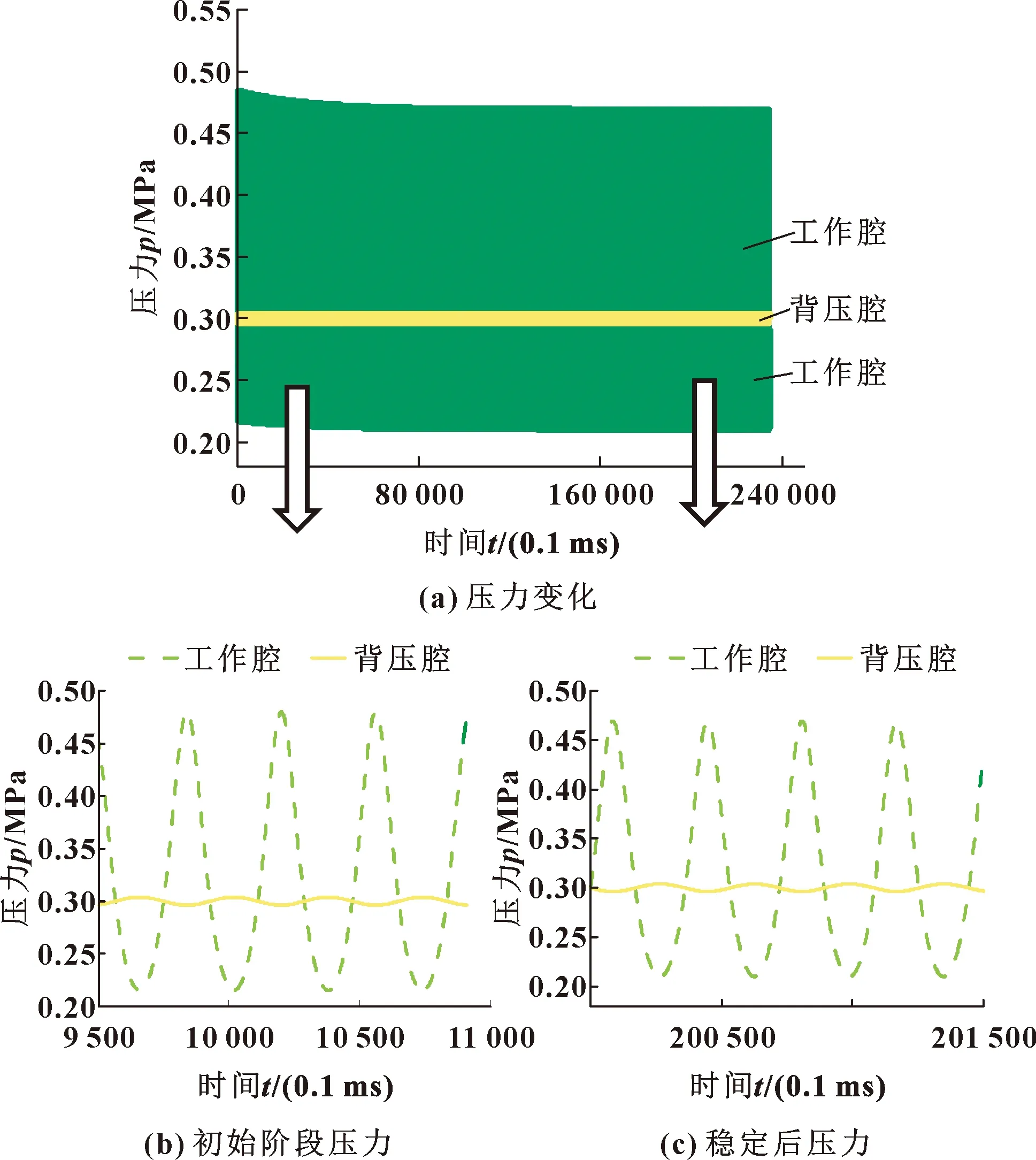
图11 间隙密封长度单侧变化时工作腔(pc)和背压腔(pb)压力分布(650个周期)

图12 间隙密封长度单侧变化时质量流量变化分布(650个周期)

4.3 间隙密封长度双侧变化

图13与14所示为运行650个周期后的循环压力以及由压差引起的质量流量变化(Q1)和速度引起的质量流量变化(Q2)。

图13(b)(c)及图14(b)(c)分别为在初始过程及稳定后的压力和质量流量细节，其规律与其他2种模型相同。

图14 间隙密封长度双侧变化时质量流量变化分布(650个周期)

5 3种密封形式对于泄漏量的影响

图15所示为一个周期内单向泄漏的质量随着周期数增加的变化。可以看出：密封长度不变时，气体泄漏量最少，密封长度单侧变化时，气体泄漏量增加，密封长度双侧变化时，气体泄漏的最多。因此，选择密封长度不变形式的间隙密封能够达到较好的密封效果。

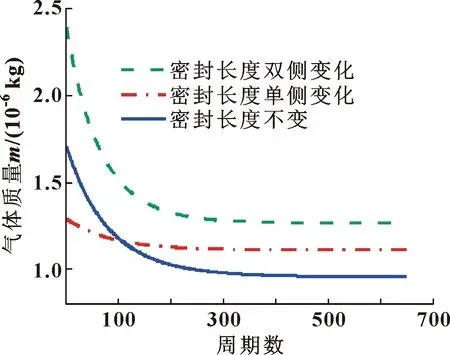
图15 泄漏气体质量随着周期数的变化

6 间隙密封的影响因素

由式(5)可知，自由活塞斯特林机间隙密封的影响因素分别有气膜厚度、活塞直径、活塞长度、运行频率、活塞行程、压差等。文献[7]中对斯特林机间隙密封泄漏量影响因素进行了权重分析，结果表明，气膜厚度和压差对斯特林机的泄漏量有极显著影响，密封长度有显著影响，其他因素无显著影响。由上述分析可知，背压腔压力波动非常小，几乎等同于初始压力，而压差由初始压力决定，因此文中选择密封长度不变的模型分析气膜厚度、背压、密封长度对泄漏量的影响。

6.1 气膜厚度的影响

图16所示为不同气膜厚度下泄漏气体质量的变化。可知，气膜间隙h越大，泄漏的气体质量越大，密封效果越差；当气膜厚度在10～30 μm时，气膜厚度对泄漏气体质量的影响趋于平缓。考虑加工及装配精度，气膜厚度在20～30 μm时为宜。

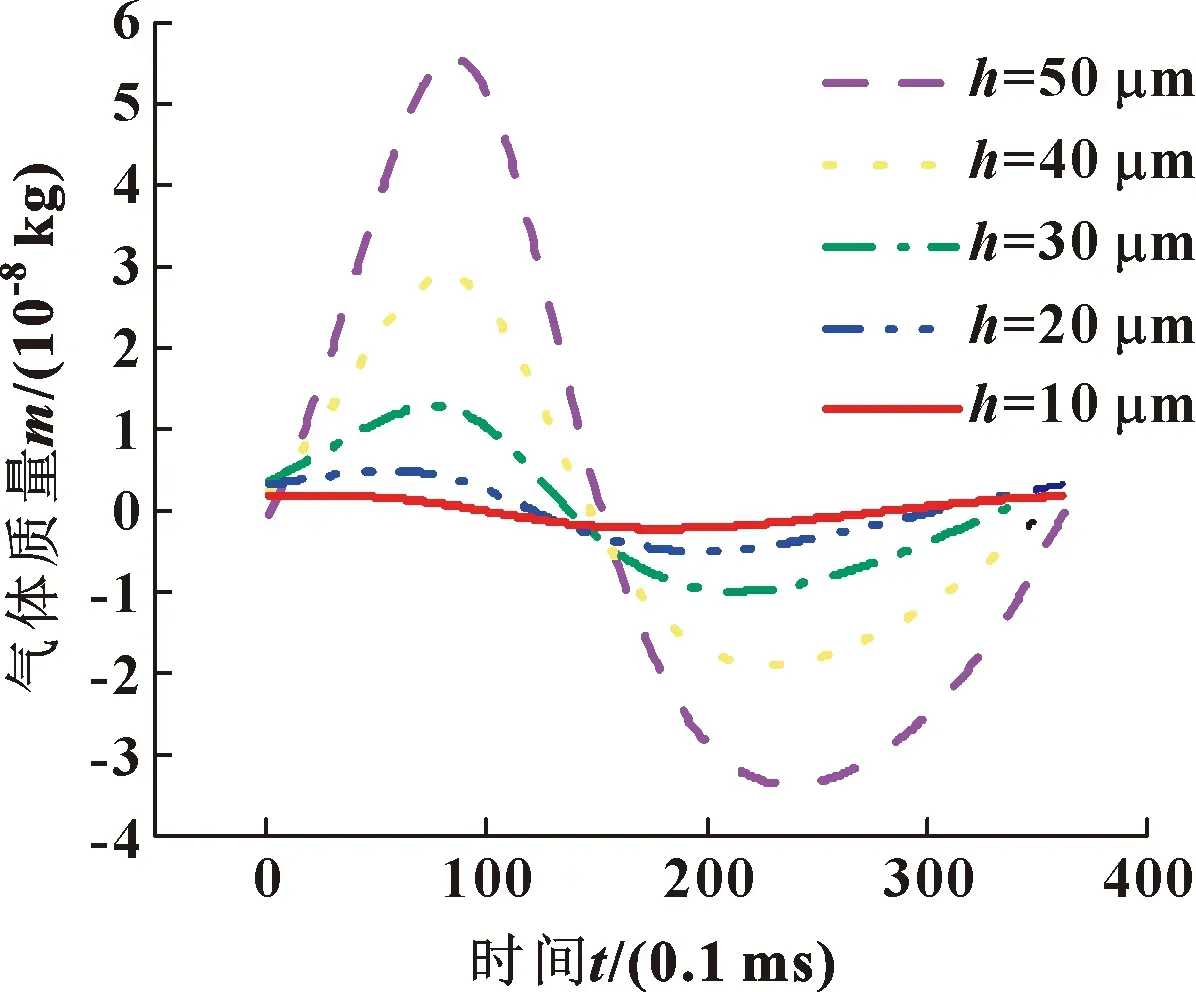
图16 不同气膜厚度下泄漏气体质量的变化

6.2 活塞长度的影响

图17示出了不同活塞长度下泄漏气体质量的变化。可知，活塞长度越长，泄漏的气体质量减少，密封效果越好；当活塞半径为2.5 cm时，活塞长度大于10 cm，即活塞长径比大于2时，密封效果良好。考虑斯特林机尺寸及空间问题，故选择活塞长度在10～15 cm范围内。

图17 不同活塞长度下泄漏气体质量的变化

6.3 背压对泄漏率的影响

图18所示为不同背压下泄漏气体质量的变化。气体泄漏量随背压的增加而增加，即随压差的增加而增加。而斯特林机内工作压力过小会影响斯特林机的正常工作，故背压选择在3～5 MPa范围内。

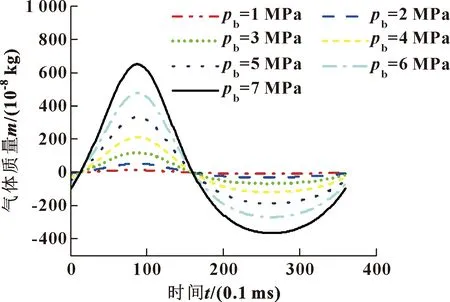
图18 不同背压下泄漏气体质量的变化

6.4 间隙密封泄漏率计算

在工程设计上，自由活塞斯特林机的间隙密封通常要求控制泄漏的气体质量在5%以内[2]。

如表2所示，文中密封长度不变的模型下，取各影响因素的极限点，点A为：活塞长度15 cm，气膜厚度20 μm，背压3 MPa；点B为：活塞长度10 cm，气膜厚度30 μm，背压5 MPa。由此计算出泄漏率的极限值，可得文中模型斯特林机间隙密封泄漏率在3%之内，因考虑到理论值与实际情况存在误差，故为后期斯特林机间隙密封泄漏量的工程应用保留了一定的裕量。

表2 间隙密封的泄漏率

7 结论

通过建立3种不同密封长度变化的间隙密封物理模型，采用时间推进法，分析求解了不同形式的密封对泄漏量的影响，研究了在压缩循环过程中气体泄漏量对压力的动态影响。主要结论如下：

(1)启动阶段，由于两腔容积不同，一个周期内气体质量会由工作腔向背压腔流动；随着时间的增加，两腔压力及泄漏的质量流量逐渐达到平衡，一个周期内净流量为0，两腔压力的压差不变。

(2) 间隙密封在启动阶段时单向泄漏量最大，随着时间的推进，泄漏量逐渐减小后达到稳定，间隙密封长度不变的模型相较于其他2种模型的单向泄漏量最少。

(3) 气体质量的泄漏随气膜厚度和背压的增加而增加，随活塞长度的增加而减小。

(4)当活塞半径2.5 cm，气膜间隙为20～30 μm，活塞长度为10～15 cm，背压为3.0～5.0 MPa时，工作腔内气体的泄漏率在3%以内，为斯特林机动力活塞间隙密封的设计提供了参考依据。