等差、等比数列性质的综合应用

樊永文

(甘肃省民乐县第一中学 734500)

近年高考数学试题中，关于等差、等比数列性质的综合应用是一个考查的热点内容，我们应引起足够重视.基于此，本文特归类举例加以说明，希望能够帮助同学们掌握一些常用的解题方法，进一步提高处理等差、等比数列综合问题的解题能力.

1 考查等差中项与等比中项的综合应用

又注意到所求式子与b无关，从而应设法消去b.

因为由②得b=2x-a，

由③得b=2y-c，

所以将之代入①可得

(2x-a)(2y-c)=ac.

即4xy-2ay-2cx=0.

评注一般地，a，b，c成等差数列⟺b是a，c的等差中项⟺2b=a+c；a，b，c成等比数列⟺b是a，c的等比中项⟺b2=ac(其中a，b，c都不为零).

2 考查两个等差或两个等比数列的交汇问题

(2)在等比数列{an}中，a1=2，前n项和为Sn.若数列{an+1}也是等比数列，则Sn=____．

解析(1)设等差数列{an}的公差为d，则

解得d=0.故所求Sn=na1=5n.

(2)设等比数列{an}的公比为q，则

a1+1=3,a2+1=2q+1,a3+1=2q2+1.

所以由{an+1}是等比数列,得

解得q=1.故所求Sn=na1=2n.

评注类似分析，可得如下一般性结论：

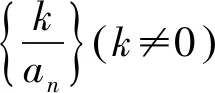
②设{an}是等比数列，且公比为q，若{an+c}(c≠0)也是等比数列，则q=1.

3 以等差数列为背景，设置等比数列问题

例3在等差数列{an}中，公差d≠0，a2是a1与a4的等比中项.已知数列a1,a3,ak1,ak2,…,akn,…成等比数列，求数列{kn}的通项kn.

所以(a1+d)2=a1(a1+3d).

所以d2=a1d.

又公差d≠0，所以d=a1.

所以an=a1+(n-1)d=nd.

从而，由题设得数列d,3d,k1d,k2d,…,knd,…是等比数列.

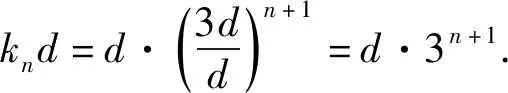
又注意到d≠0，故可得所求kn=3n+1.

解法2同解法1，先求得a1=d，

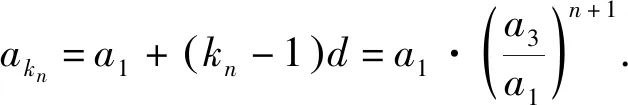
所以kn·d=d·3n+1.

又注意到d≠0，故可得所求kn=3n+1.

评注上述两种解法的区别在于：前者先明确所给等比数列的各项，再运用等比数列的通项公式；后者则是考虑akn在两个数列中的不同位置，并灵活运用等差、等比数列的通项公式进行综合分析.

4 考查等差数列与等比数列交错接龙

解析因为数列a1,a2,…,a6是以a1=-3为首项，且以d1=1为公差的等差数列，所以可得a6=-3+5×1=2.

于是，由数列a6,a7,…,a12是以q1=3为公比的等比数列，得a12=a6·q6=2×36.

由数列a12,a13,…,a18是以d2=-2为公差的等差数列，可得a18=a12+6d2=2×36+6×(-2)=2×36-12.

评注在具体情景下，多次反复运用等差数列和等比数列的通项公式，是本题顺利求解的关键所在.整体看，本题设计较好，情景新颖，不仅考查了学生的阅读理解能力，而且也考查了学生在新情景下灵活运用所学等差、等比数列知识分析、解决问题的实际能力.

5 以行与列的形式，考查等差数列和等比数列通项公式的活用

(1)求公比q的值；

(2)求a4k；

(3)求ann；

(4)求a11+a22+…+ann.

图1

于是，由第4列的数组成等比数列,得

(2)因为第4行的数组成等差数列，

所以a4k=a42+(k-2)·(a43-a42)

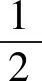
(4)根据(3)可知

④

⑤

由④-⑤,得

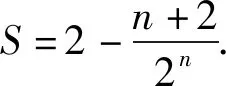
评注(1)本题以“方阵”为载体，考查了在新情景下学生灵活运用等差、等比数列知识处理问题的能力，而解题的关键就是利用等差、等比数列推广的通项公式及错位相减法.

(2)根据等差、等比数列的通项公式，很容易证得推广的通项公式：

①若{an}是等差数列，则an=am+(n-m)d；

②若{an}是等比数列，则an=am·qn-m.

综上，处理有关等差、等比数列性质的综合运用问题，首先要认真审题，看清题目已知条件；其次，要能够将等差、等比数列的性质在解题中加以灵活、准确运用.显然，通过上述的归类剖析，可帮助我们进一步熟练掌握等差、等比数列的有关性质，进而提高对新情景的适应能力以及对相关知识的综合运用能力，进一步提升学生的数学综合素养.