赏析新情景数列问题

张子芳

(甘肃省民乐县第一中学 734500)

本文侧重赏析以下四类新情景数列问题的解析，旨在帮助同学们明确此类问题的求解策略，进一步巩固所学数列知识在解题中的灵活应用，进而提高分析、解决问题的实际能力.

1 “周期”型数列问题

在数列问题中，当正整数n较大时，要计算an或Sn，一般是利用等差或等比数列的通项公式、求和公式求解；若数列不是等差或等比数列，则往往需要优先考虑数列的周期性.

例1在数列{an}中，已知a1=2，a2=3，当n≥2时，an+1是an·an-1的个位数，则a2022=____.

解析根据题设得a1=2,a2=3，a3=6,a4=8,a5=8,a6=4,a7=2,a8=8，a9=6,a10=8,a11=8,a12=4,a13=2,a14=8,….

所以据此可知数列{an}中的各项从第3项起，会反复出现数字6,8,8,4,2,8，即具有周期性(以6为周期).

又注意到2022=2+336×6+4，

故易知所求a2022=4.

评注通过罗列数列的前几项，可归纳获得该数列的周期性，这是本题求解的关键所在.

2 “分段”型数列问题

若所给原数列递推式是分段函数的形式，则有意识地去探求新数列的相邻两项之间的紧密联系，往往会发现隐藏在其中的规律、特点，从而便于迅速找到解题思路.

(2)根据题设,得

易知bn≠0.

3 “新运算”型数列问题

数列问题中，如果题目给出了“新运算”，那么需要我们先认真阅读，准确理解、认识“新运算”的特点；然后再结合相关数列知识加以灵活分析、求解.

(1)若an=2n-1，则Q4=____；

(2)若Qn=n2(n∈N*)，则an=____.

解析(1)因为an=2n-1，

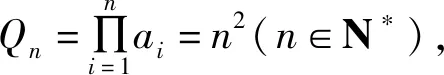
所以a1a2…an=n2(n∈N*).

①

于是，可知a1a2…an-1=(n-1)2(n≥2).

②

从而，当n≥2时，由①÷②可得

又当n=1时，an=a1=Q1=1，显然不满足上式成立.

评注由①②两式求an时，必须要注意成立的前提条件是n≥2,否则极易出错.

4 “新定义”型数列问题

数列问题中，如果题目给出了“新定义”，那么需要我们先认真学习，彻底搞清“新定义”是如何描述的；然后再结合相关数列知识加以灵活分析、求解.

例4 对任意x∈R，设[x]表示不超过x的最大整数，则函数f(x)=[x]叫做高斯函数(又称“取整函数”).

(2)若bn=f(log2n),n∈N*，Tn是数列{bn}的前n项和，求T1024.

解析(1)通过观察前n项，得

所以S30=0×(3-1)+1×(6-3)+2×(9-6)+…+9×(30-27)+10

=3(1+2+…+9)+10=145.

(2)通过观察前n项，得

评注本题先将数列通项写成关于“n”的分段函数的形式，这样有利于帮助我们顺利探求规律、简洁求和.此外，要注意准确写出数列通项公式中各段“n”的取值范围.

总之，上述归类举例解析，不仅拓宽了我们的解题思维视野，增长了见识，而且可帮助我们积累一些求解数列新情景问题的经验，同时强化了相关数学知识、思想方法在解题中的灵活、综合运用能力.

一般来讲，处理新情景数列问题需要过好三关：第一关，“心理关”，需要在心理上克服畏惧、胆怯等心理活动，必须具有积极的挑战、探究、钻研精神；第二关，“阅读理解关”，通过认真阅读、思考，有利于审清题意，知道题设条件是什么，明确目标问题是什么；第三关，“运用关”，能够将所学数列知识与其他相关知识在解题中加以灵活运用，从而顺利解决目标问题.