对一道系数和为定值试题的探究

高继浩

(四川省名山中学 625100)

1 试题呈现

(1)求椭圆C的标准方程；

2 解法探究

视角1 (设线法)设出直线l的方程并与椭圆方程联立,通过向量关系将λ1,λ2用两根表示,再借助韦达定理求解.

解法1(正设直线)显然直线l的斜率存在,F(1,0),设A(x1,y1),B(x2,y2),直线l的方程为y=k(x-1),与椭圆方程联立消去y，得

(1+2k2)x2-4k2x+2k2-2=0.

由韦达定理,得

而P(0,-k),则

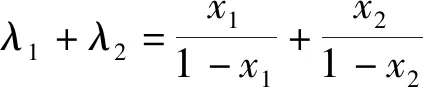
解法2(反设直线)易知F(1,0).当直线l的斜率不为零时,设A(x1,y1),B(x2,y2),直线l的方程为x=my+1(m≠0).

与椭圆方程联立消去x,得

(m2+2)y2+2my-1=0.

由韦达定理,得

故λ1+λ2=-4.

综上,λ1+λ2=-4.

视角2(代点法)直接设出A,B,P三点的坐标,通过向量关系解出A,B两点的坐标并代入椭圆方程,再借助韦达定理求解.

x1=λ1(1-x1),y1-n=-λ1y1.

代入椭圆方程,得

所以λ1,λ2是关于x的方程x2+4x+2-2n2=0的两根,故λ1+λ2=-4.

视角3(参数法)借助椭圆参数方程设出A,B两点的坐标,通过向量关系得到参数关系,再利用和差化积与积化和差公式求解.

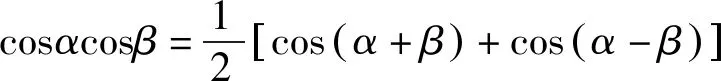
3 推广引申

将试题第(2)问进行一般化推广得到：

前面的四个解法中,解法3较为简洁,下用此法证明命题1.

x1=λ1(c-x1),y1-n=-λ1y1.

代入椭圆方程,得

同理可得

所以λ1,λ2是关于x的方程b4x2+2a2b2x+a2(b2-n2)=0的两根.

将命题1中右焦点改为x轴上一点后得到：

将命题1、命题2引申到双曲线中,得到：

命题2至4的证明过程与命题1类似,略.

在抛物线中有：

证明设A(x1,y1),B(x2,y2),P(0,n),则

x1=λ1(t-x1),y1-n=-λ1y1.

代入抛物线方程,得

同理可得

4 对偶拓展

受文[1]启发,将命题2和命题4中点E的位置改为y轴上,分别得到：

证明设A(x1,y1),B(x2,y2),P(m,0),则

x1-m=-λ1x1,y1=λ1(tb-y1).

显然λ1≠-1,

代入椭圆方程,得

同理可得

所以λ1,λ2是关于x的方程a2(1-t2)x2+2a2x+a2-m2=0的两根.

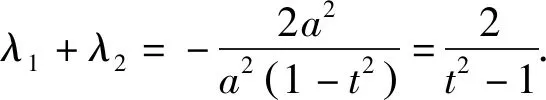
命题7的证明过程与命题6类似,略.

5 方法运用

我们对命题的证明采用了前面的解法3进行,借助同构方程思想使得问题的解决过程简洁明了,运算量小.下面给出两个变式练习题,供参考.

证明易知F(1,0),设A(x1,y1),B(x2,y2),P(4,n),则

x1-4=λ1(1-x1),y1-n=-λ1y1.

显然λ1≠-1,

所以λ1,λ2是关于x的方程9x2-4n2-36=0的两根.

故λ1+λ2=0.

x1-t=-λ1t,y1=λ1n.

代入抛物线方程,得

所以λ1,λ2是关于x的方程t2x2-2(t2+2n)x+t2=0的两根.

故λ1·λ2=1.