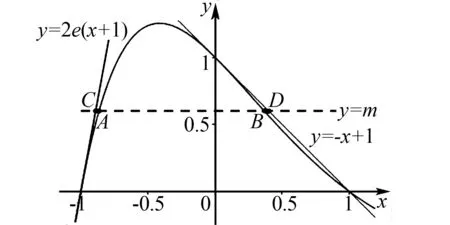
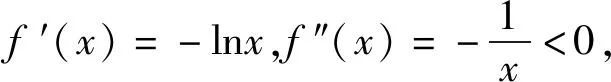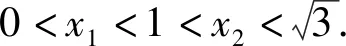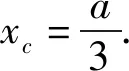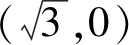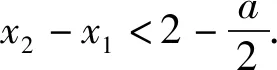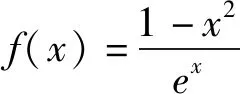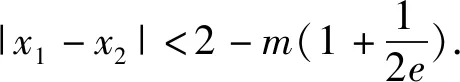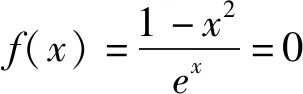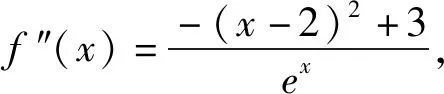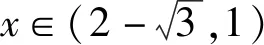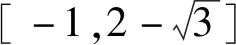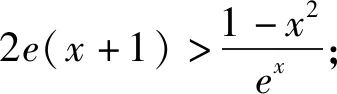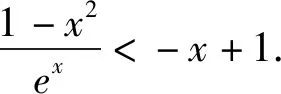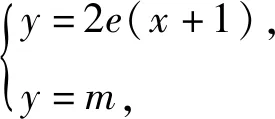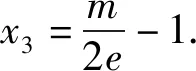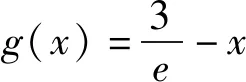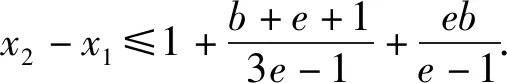切线放缩在函数双零点问题中的应用

林国红

(广东省佛山市乐从中学 528315)

函数的凹凸性是高等数学研究函数的性质之一，虽然高中数学中没有对函数的凹凸性作具体要求，但以函数凹凸性为背景的试题屡见不鲜，这些试题情景新颖，能考查学生的创新能力和潜在的数学素质，常作为压轴题出现.

下面简单介绍函数的凹凸性，并从函数凹凸性的视角，利用切线放缩对一类双零点的函数压轴题进行探究，供大家参考.

1 函数的凹凸性及常用性质

1.1 凹凸函数的定义

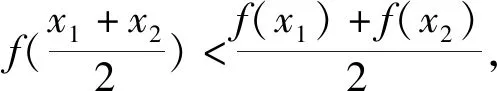
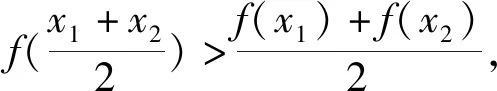
1.2 凹凸函数的常用性质

1.2.1 凹凸函数的判定定理

设f(x)在[a,b]上连续，在(a,b)内具有一阶和二阶导数，那么：

若f(x)在(a,b)内有f″(x)>0，则f(x)在[a,b]上是下凸函数；

若f(x)在(a,b)内有f″(x)<0，则f(x)在[a,b]上是上凸函数.

1.2.2 切线放缩(切线不等式)

若f(x)在区间I为下凸函数，则对于∀x0∈I，有f(x)≥f′(x0)(x-x0)+f(x0)；

若f(x)在区间I为上凸函数，则对于∀x0∈I，有f(x)≤f′(x0)(x-x0)+f(x0).

评注下凸函数图象上任意一点的切线在函数图象的下方，上凸函数图象上任意一点的切线在函数图象的上方.

2 切线放缩估计函数双零点范围的基本原理

若f″(x)>0，则f(x)在区间Ⅰ为下凸函数，因此f′(x)在区间I上单调递增，从而f(x)最多有一个最小值，即下凸函数的图象仅有两种形态：无最小值型(如图1)和有一个最小值型(如图2).

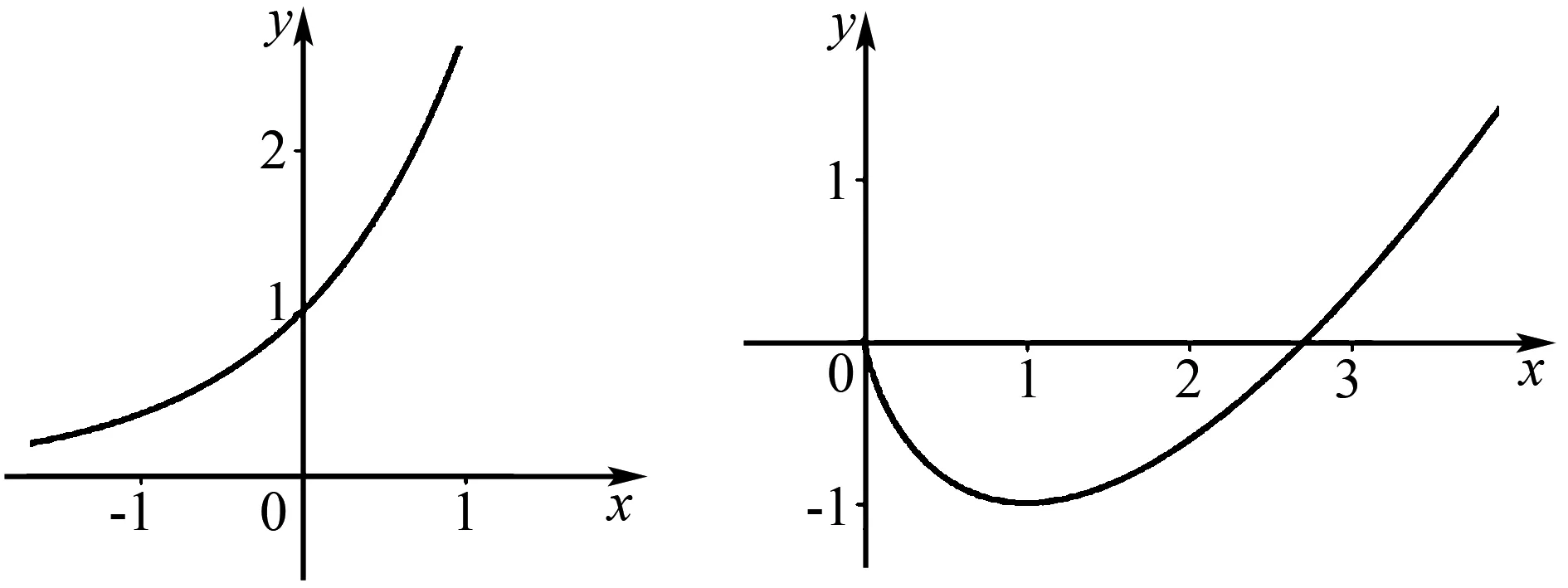
图1 图2

若f(x)在区间Ⅰ为下凸函数，且f(x)有最小值，f(x)的图象与y=m交于A(x1,m),B(x2,m)两点，f(x)在点C处的切线l1，在点D处的切线l2(如图3).这样我们就可以利用切线l1与l2和y=m的交点来估计x1与x2相关的范围，这是切线放缩估计函数双零点范围的基本原理.

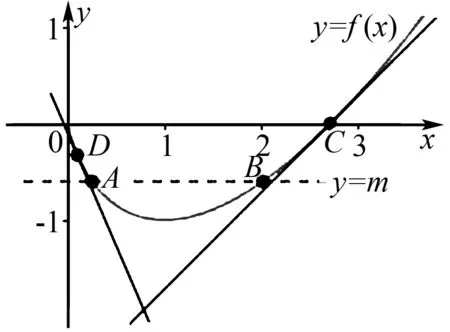
图3

对于上凸函数，其原理与下凸函数类似，限于篇幅，不再给出.

3 典型例题

例1 (2021年新高考Ⅰ卷22题)已知函数f(x)=x(1-lnx).

(1)讨论f(x)的单调性；

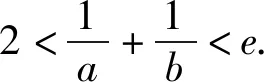
解析(1)f(x)的定义域为(0,+∞)，且f′(x)=-lnx，故f(x)在(0,1)上单调递增，在(1,+∞)上单调递减.

(2)由(1)可知，f(x)在(0,+∞)上只有一个极值点1.

因为blna-alnb=a-b

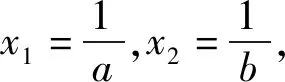
已知f(x1)=f(x2)，证明：2

下面仅证x1+x2

图4

设f(x)与y=m,m∈(0,1)交于A,B两点，A(x1,m),B(x2,m)，则0

由于f(x)在点(e,0)处的切线方程为

y=-x+e

设切线与y=m交于点C(xc,m)，则

xc=-m+e.

直线y=x与y=m的交点为(m,m)，如图4，所以0

两式相加，即得x1+x2

例2 (2021年湖北部分重点中学联考21题)已知函数f(x)=3x-x3，若关于x的方程f(x)=a有两个正实数根x1,x2，且x1

(1)求实数a的取值范围；

解析(1)a的取值范围为(0,2)，过程略.

(2)由于f′(x)=3-3x2，f″(x)=-6x，可得f(x)在(0,+∞)上是上凸函数.

图5

如图5可知，

x2-x1

(1)求函数f(x)的零点x0，以及曲线y=f(x)在x=x0处的切线方程；

所以曲线y=f(x)在x=1处的切线方程为

由于f′(-1)=2e，

所以曲线y=f(x)在x=-1处的切线方程为

y=2e(x+1).

则f′(0)=-1，且f(0)=1.

所以曲线y=f(x)在x=0处的切线方程为

y=-x+1.

从而当x∈(-1,0]时，直线y=2e(x+1)在曲线y=f(x)上方.

当x∈(0,1)时，直线y=-x+1在曲线y=f(x)上方.

因为方程f(x)=m(m>0)有两个实数根x1,x2，设直线y=m与曲线y=f(x)交于A,B两点，则A(x1,m),B(x2,m)，直线y=2e(x+1)与直线y=m交于点C(x3,m)，直线y=-x+1与直线y=m交于点D(x4,m)，如图6.

图6

解得x4=1-m.

如图6可知，

|x1-x2|<|x3-x4|

图7

以函数凹凸性中的切线放缩为命题背景的试题还有很多，通过以上几道例题，不难体会函数凹凸性等相关知识的丰富性，虽然函数凹凸性不属于高中数学的内容，将其“镶嵌”在高中试题中可谓独具匠心.这也表明：高等数学的相关理论是命制一些具有创新力与区分度试题的重要来源.若能多了解一些函数凹凸性的相关理论知识，可以“登高望远”，便于找到问题的本质内涵，养成对试题背后的内在关系进行分析与思考习惯.

最后提供两个题目作为练习，以加深体会切线放缩的解题思路.

练习1(2020年哈尔滨二模理21题)已知函数f(x)=mxlnx-(m+1)lnx，f′(x)为函数f(x)的导数.

(1)讨论函数f′(x)的单调性；

练习2(2020年1月清华大学中学生学术能力测试理21题)已知函数f(x)=(x+1)(ex-1).

(1)求f(x)在点(-1,f(-1))处的切线方程；