整合知识与思维的结构化分析模式构建与应用

艾 静 熊建文

（1.广州市教育研究院，广东 广州 510062；2.华南师范大学物理与电信工程学院，广东 广州 510006）

在教育领域，碎片化与结构化被视为两种截然不同的样态，碎片化会造成学生在学习过程中出现认识深度不够、推理不畅、思维僵化等问题，当前学者多提倡从“整合”“结构化”等视角研究教育问题.

1 结构化分析的思考

1.1 “整体人”培养的构念对“整合”“结构化”分析的启示

新课标在学科课程内容上要求以学科大概念为核心，对学科课程内容进行结构化整合，并借助结构化的情境设置，使学科核心素养得以落实，体现出对“整合”“结构化”的重视与应用.

在具体教学中，多数教师缺乏“整合”“结构化”的思维意识或教学设计与实施能力；在物理学习中，学生常因审题缺乏逻辑、解题无处下手、抓不住关键点等学习障碍而影响问题解决，其主要原因在于学生知识的零散化和思维的碎片化；［1］在命制试题时，命题双向细目表或命题蓝图的设计，常要求将各试题包含的知识与思维分别以文字方式列出，以核验知识点或思维能力考查的覆盖情况，这一方式在表征试题考查信息时，难以直观呈现试题考查的知识与思维间的内在关联，未能全面反映试题在知识与思维方面的考查目的.上述现象都反映出当前学科教学中，无论是教、学或是评价上，仍受到“碎片化”影响.

从对“整体人”素养的培养［2］来说，知识结构与思维结构存在紧密关联，且具有内在一致性，思维结构以既有的知识结构为基础，思维过程反作用于知识结构，会引起知识结构的改变与重构，使其从线性关联走向立体关联，而知识结构需在问题解决过程中才能得以建构和发展.［3］因此，问题设计应整合解题涉及的知识与思维，使之形成关联紧密、结构清晰的具有稳定图式表征的问题空间，以考查学生通过问题解决所形成的知识与思维结构，进而促进“整体人”素养的培养.

1.2 整合知识与思维进行结构化分析的可能与可行

近年来，在“思维可视化”研究浪潮的推动下，借助知识结构的外化来发展思维能力的做法已受到广泛认可，并付诸行动，研究者均意识到了知识水平与思维水平存在正相关，但对知识结构的样态、水平与思维水平间如何建立清晰明确的关系仍存在较大疑惑.

比格斯SOLO 分类理论中的“思维结构”是指学习者为解决具体问题，对知识结构进行转换、重组（知识结点的断开与连接）而呈现出的动态结构.当下，“真实”的客观世界被默认是普遍联系、多层面多角度的复杂立体结构.就知识结构而言，比格斯5个水平反映出各水平由“线性结构”“平面结构”“立体结构”逐步逼近客观世界之“真实结构”.在比格斯“思维结构”理论的启发下，笔者认识到知识与思维两者的结构存在内在关联和一致性.由此可初步推测，对具体问题所包含的知识与思维进行结构化分析是可能且可行的.

以评价促进教学的理念在当前教学中得到普遍认可，核心素养的培养更多地依赖其评价的有效性.相似的试题形式下，核心素养评价的关注点已经从知识点的“量”转变为知识点所形成的“结构”，［1］说明学习者所形成的内部知识结构才是素养生成的内在基础，其目的是引领、促进核心素养要求的复杂关联的高水平知识与思维结构的生成.

在设计一套评价试卷时，教师基于知识与思维视角，需要依次考虑如下问题：本次评价需要考查学生掌握的知识点有哪些？ 对知识点的水平分布有何要求？ 会考查到何种思维？ 知识点与思维之间有何关联？ 这些知识点和思维能力需要在学生头脑中形成什么样的结构？ 整套试卷所包含的多个试题，每个试题是否实现对预设知识与思维结构的考查，这些试题是否共同达成对考查范围内所涉及的知识与思维结构的全面覆盖？ 知识与思维的结构化分析，旨在以直观、立体的方式呈现各试题所包含的上述信息，以便于对试卷进行质量分析.

2 结构化分析理论模式的构建

2.1 结构化分析的要素

不同学科的问题设计，其背后运用的学科知识和思维要素不同，知识和思维的相互关联与作用，会产生不同的障碍点.结构化分析的要素包含3个方面：知识、思维、障碍点.

（1）知识点与知识层级.

“整合”成为基础教育阶段课程改革的核心理念，是当前教育研究的一种思维方式，为学科大观念的提出奠定了基础.2017版普通高中物理课程标准中的物理观念即学科大观念，各物理观念之间存在相互关联，构成了整个高中阶段知识体系.依据高中物理知识层级关系构建的方法，［4］可将知识点划分为由低到高的4 个水平层级，图1 为动力学知识体系的知识层级关系图.

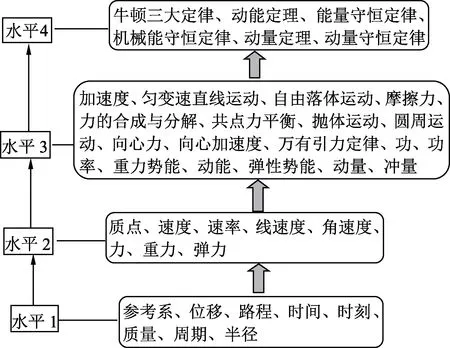
图1 “动力学”知识层级关系图

各知识点在构建问题空间时的作用表现出强或弱的差异.强作用的知识点主要是关联到问题解决视角，如水平4的知识点，即观念层的核心知识；弱作用的知识点则是对问题空间创设起到支撑作用的基础知识，如水平2和水平1的知识.问题的设问往往多为水平1到水平3的各层级具体知识点.在问题设计中，各知识点或各知识层级之间存在直接或间接的联系，低水平层级的知识点是高水平层级知识点构建的知识基础，以具体试题为例，分析其所包含的知识点及知识层级如表1所示.

表1 具体试题知识点、知识层级分析示例

对倾向于考查基础性的试题，其多考查较低水平层级的知识，包含的知识点少、知识点之间的关联简单；对倾向于考查综合性的试题，则多会具有整合性特征，考查的知识点多且知识点之间的关联复杂.因此，判断试题对基础性或综合性等考查的倾向性时，也可结合具体试题中所包含的知识点在各层级考查的数量及知识结构框架的复杂与否等进行评定.

（2）思维种类与思维层级.

安德森等人（2001）对布鲁姆教育目标分类学修订，安德森作出的修订主要是将布鲁姆分类法中由使用名词变为运用动词界定思维种类，即记忆、理解、应用、分析、评价和创造.当前教育研究中普遍将前三者称为低阶思维，将后三者称为高阶思维，说明各思维要素具有一定的层级性.在2017版高中物理课程标准中，将解决物理问题所需的科学思维，从建模、推理、论证、质疑等4个维度划分为由低到高的5个水平.［5］

对问题解决过程中所涉及的思维要素及思维层级的分析，可将上述两者均纳入到思维结构化分析中，前者更多的表现为将知识与思维整合后的认知过程要求，后者表现为物理学科领域对思维的具体要求，两者从不同角度表现学科问题解决过程中的思维特征.

（3）障碍点的分类.

试题中障碍点设计的分析主要分为3 类：一是由于关系理解困难出现的障碍点；二是因逻辑推理的严谨与深度要求较高出现的障碍点；三是在重要知识的迁移应用中出现的障碍点.

三类障碍点都体现出知识与思维的紧密关联.关系理解需要通过思维建立相关知识点之间的联系，要区分知识点的区别，要明了其在解决具体问题、构建思路中的作用；逻辑推理的严谨与深度对知识点的量、知识本质的理解、思维的种类与水平要求更高；重要知识往往关联多个低层级知识点，其迁移建立在理解、应用、分析等基础上，对思维要求较高.三类障碍点的形成不能简单地归为知识障碍或思维障碍，而是由两者共同作用形成.

2.2 结构化呈现的方法

（1）SOLO 分类理论对结构化呈现的启示.

SOLO 分类理论将学生学习结果表现出来的思维结构分为前结构、单点结构、多点结构、关联结构和拓展抽象结构，学生在学习中普遍存在5种思维结构.SOLO 分类体系是思维之样态、水平从结构视角的诠释，如图2（a）所示.由图2（a）启示，知识与思维结构化分析，可根据具体试题内容构建不同的立体图形，以直观呈现其知识与思维的内容与水平，以题目1 内容为例，可得到如图2（b）所示结构化图形.

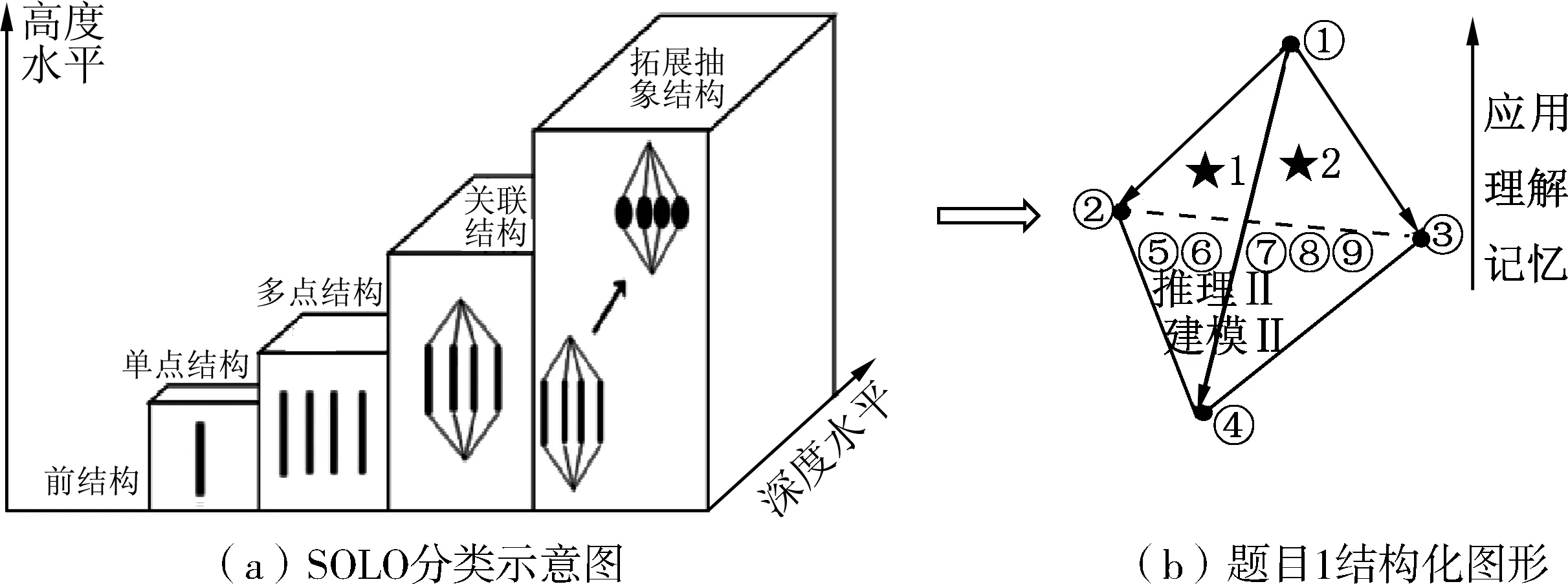
图2

知识与思维结构的形成与发展是结构顶点和边的变化，顶点和边的状态上记载了思维水平的足迹.在内容层面考查顶点的丰富性，在结构层面考察边的建立与连接情况.在具体分析中，首先关注重要知识结点是否有效覆盖，即看顶点的建立，问题涉及的知识点会发生结构层次上的关联，进入多点之间连接，生成更丰富的知识结构.若不同的顶点与边构成方向明确、清晰的立体结构的时候，学生在问题解决过程中也会经历顶点的生成与调整，边的生成与强化等.

问题设计会呈现知识与思维结构的应然状态，应预设好各问题的预期结构.在解决特定问题时，学生知识与思维结构中所包含的知识点数量众多，就目标描述而言，试图全面列举显然不可能，本研究中只关注作为问题解决主要知识点.

（2）立体结构设计说明.

知识的点样状态会随着时间推移，容易遗忘，线性思维缺乏灵活性，知识与思维的结构化能紧密联系相关内容，将问题解决的时间、空间维度整合起来，构成具备稳定结构的问题空间.［6］在问题的知识与思维结构化分析中，主要理清4 个方面的问题，其内容及具体做法如表2所示.

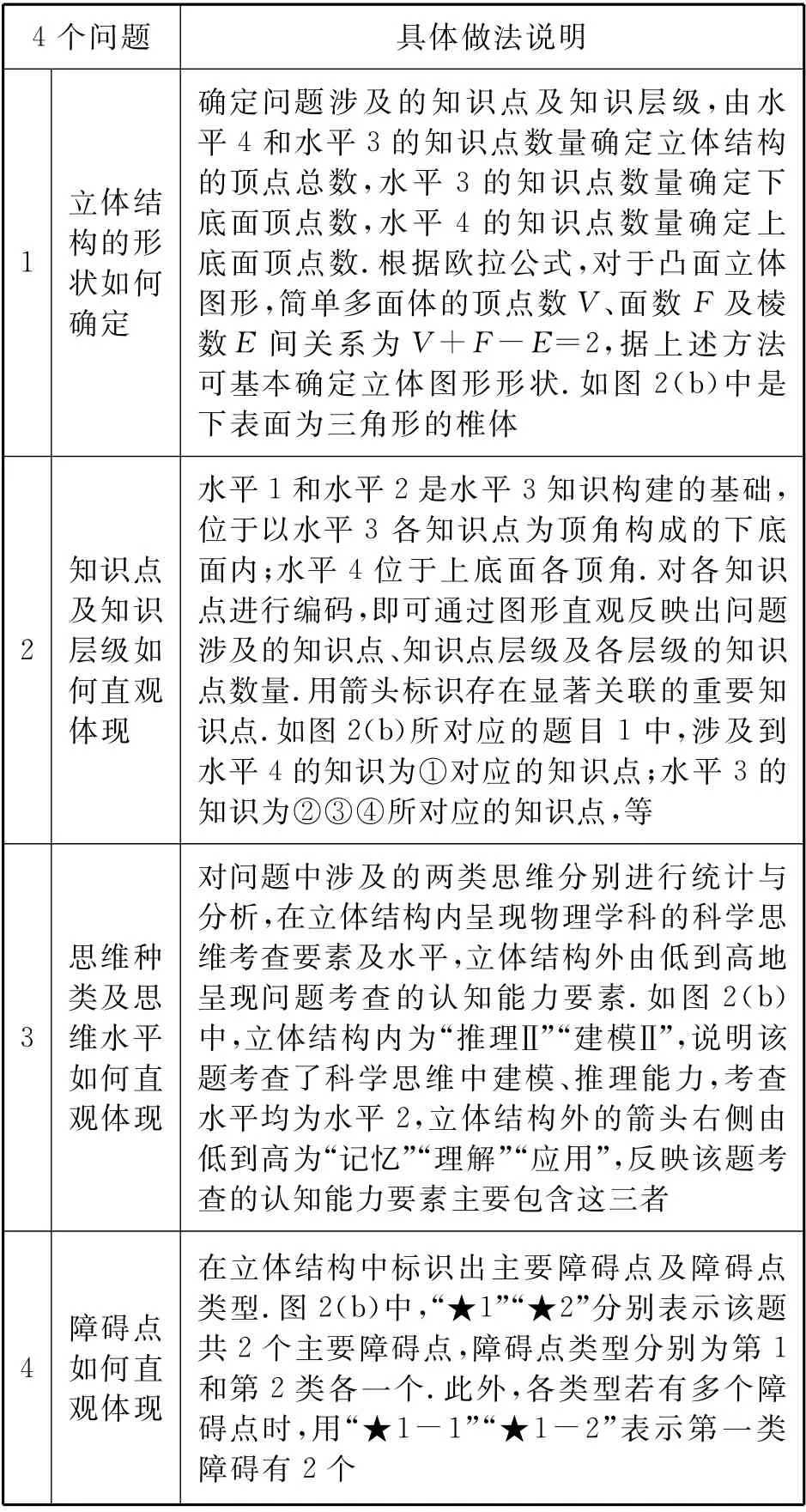
表2 立体结构设计的问题与做法说明

由表2可知，不同问题绘制的立体图形不同，立体图形的绘制能直观呈现问题涉及知识、思维和障碍点信息.通过上述结构化分析，可知：（1）立体图形顶点数越多，综合性越强.尤其是上底面顶点数越多、其图形结构越复杂，综合性越强；一般上底面的顶点数会少于下底面的顶点数，主要在于水平3 各知识点是水平4 知识点的基础.（2）绘制的图形可能会受到个体主观因素影响.因此，在设计试题时，应采用集体研讨或采用统一标准等方式来进行结构化分析，以减少因个体主观评价或评价标准不一致导致的偏差.

2.3 结构化呈现的样例

对试题所承载的知识与思维进行结构化分析，主要包含以下4个方面：（1）知识点（层级）及认知水平；（2）思维样态，包含建模、推理、论证、质疑等，以及对应水平层次；（3）试题中障碍点设计的数量及种类分析；主要是面向关系的理解、逻辑推理的严谨与深度、还是重要知识的迁移应用等三类障碍；（4）知识与思维关联结构及障碍点分布简图.通过具体试题的结构化分析，可立体、直观地呈现试题承载的知识认知负荷与思维多样化及深度，具体见表3所示.

表3 知识与思维结构化分析示例与内容

题目 知识与思维关联结构及障碍点分布简图与说明题目2.（2022年广东物理）“祝融号”火星车需要“休眠”以度过火星寒冷的冬季.假设火星和地球的冬季时长约为地球的1.88倍.火星和地球绕太阳的公转均可视为匀速圆周运动.下列关于火星、地球公转的说法正确的是（A）火星公转的线速度比地球的大.（B）火星公转的角速度比地球的大.（C）火星公转的半径比地球的小.（D）火星公转的加速度比地球的小（1）知识（层级）与认知负荷水平：①牛顿第二定律（4）：应用；②圆周运动（3）：应用；③万有引力定律（3）：应用；④向心加速度（3）：理解；⑤线速度（2）：理解；⑥角速度（2）：理解；⑦周期（1）：理解；⑧半径（1）：记忆.（2）思维样态（水平层级）：建模（水平Ⅱ）；推理（水平Ⅱ）.（3）可能的障碍点分析：★1.无法从题设信息中获得火星与地球绕太阳做匀速圆周运动的周期、半径等关系；★2.无法灵活应用各物理量表示万有引力提供向心力的表达式，并结合火星与地球绕太阳的周期大小关系推理其他各物理量大小关系images/BZ_40_1724_1495_2148_1869.png

3 基于结构化分析评价问题设计质量

3.1 结构化分析的评价要点

试题知识与思维结构化分析可间接反映问题设计特征，进行评价时，可从以下方面进行分析：（1）立体图形的复杂程度.立体图形越复杂，该题综合性越强，其难度一般越大.立体图形的复杂程度主要看其上、下表面顶点数，其对应的是知识层级中，水平较高的知识点数量，往往会涉及更复杂的关系的建构，综合性强、难度大.（2）立体图形中标识的科学思维种类越多、水平越高，问题越复杂.这类问题往往对应较复杂的立体图形.（3）障碍点的数量与类型间接反映问题的难度.障碍点数量越多问题越复杂.（4）立体结构图形越复杂的问题，认知要求越高.

3.2 通过结构化分析比较不同问题设计的特征与启示

依据结构化分析与评价方法，对2021 年和2022年广东物理卷中4道题进行对比分析，从而明晰命制的试题特征，以获得教学启示.

由表4 所示结构化分析中的立体图形，可清晰表征并区分各试卷所考查的知识、思维等方面的差异，初步评定试题质量与难度，核查整卷知识、思维、认知等方面信息，以便快速形成对整卷内容的初步认识.

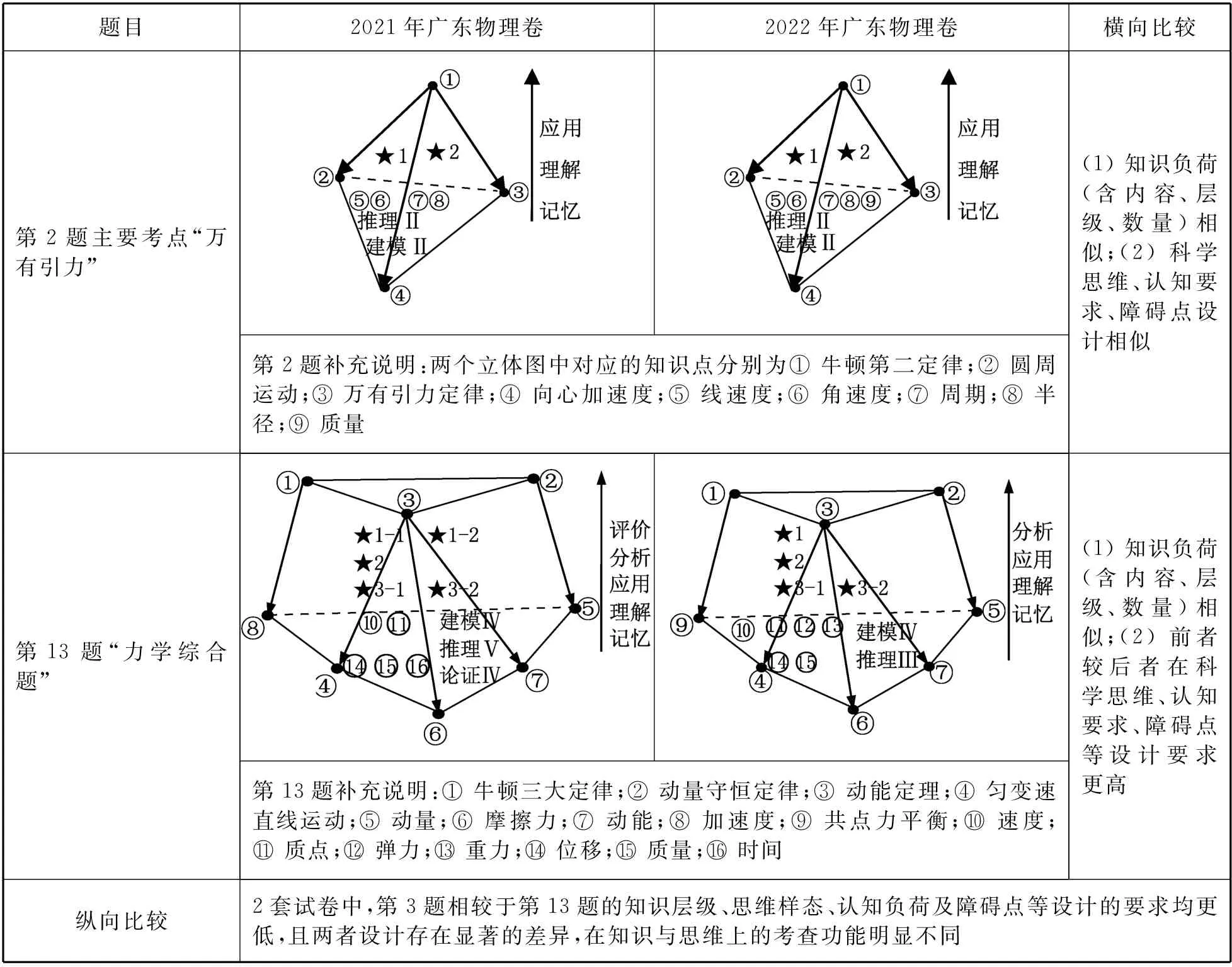
表4 结构化分析横、纵向比较的实例与启示

综上，从试题所承载知识的认知负荷、思维的多样化与深度视角分析试题质量时，可以从知识层级水平、认知负荷水平、所考查思维的种类与水平、障碍点的设计等多个方面建立标准，从上表实例可初步得出（1）试题承载的知识点及知识点水平层级、认知负荷水平可间接判断试题的难度；（2）试题所考查的思维的种类与水平也可间接判断难度与能力的匹配情况；（3）试题中障碍点的设计分析可间接反映试题的难度、信度等；（4）绘制的试题知识与思维关联结构及障碍点分布简图，可间接反映试题难度、信度、难度与能力匹配情况.［7-8］