多星多任务分配问题建模与优化算法研究

杨 超，周庆瑞，王 辉

1.中国空间技术研究院钱学森空间技术实验室,北京 100094

2.齐鲁空天信息研究院,济南 250100

0 引 言

巨星座技术的发展对天基遥感领域带来了前所未有的机遇，很多行业应用都对天基遥感系统提出了更高的需求，使得观测目标日趋多样化、观测范围更加广泛，对遥感卫星复杂任务的管理能力提出了巨大挑战.针对模式复杂、数量巨大的观测任务需求，如何统筹安排遥感卫星的资源，达到充分合理利用天基资源和最大化满足用户需求，成为目前遥感领域亟待解决的问题[1-3].

卫星任务分配问题具有复杂性，组合多样性的特点，已被证明是一个多约束、多冲突、非线性的NP-hard问题.随着在轨卫星数量以及观测目标需求的不断增加，卫星任务分配问题的指数爆炸特征十分明显.在现有的卫星任务分配研究中，大部分是将成像卫星任务分配问题建模为优化问题，然后采用优化算法进行求解.

文献[4]提出了通过不断迭代进而求解的方法，按照一定的规则对所有任务进行排序分组，对每组的算法采用完全搜索算法进行求解.但是该优化算法只适合小规模的单星成像问题，针对大规模的多星联合成像问题难以求解.SHERWOOD等[5]将所有任务按照时间窗进行先后排序，优先完成时间窗早的任务，并根据任务的优先级对已完成的任务进行替换.苗悦等[6]设计了基于目标等级，以任务筛选过程为核心的多星分层无择优和多星分层择优2种自主任务规划算法.阮启明等[7-10]等针对多星任务规划问题开展了群智能优化算法的研究，对蚁群算法、遗传算法、模拟退火算法进行研究和改进.刘晔伟等[11]采用基于贪婪算法与合同网协作的规划算法，可以实时高效地完成动态任务规划问题.

综合分析，蚁群算法和模拟退火算法具有较好的性能.但是单独使用一种算法去求解多星任务规划问题通常具有其局限性，例如蚁群算法利用了信息素的正反馈特性，能够在较快的时间内搜索到可行解，但是算法易陷入早熟，即某路径的信息素浓度明显高于其他路径时，导致算法会过快地收敛于该路径[13-15].模拟退火算法虽然局部搜索能力强，不易于陷入局部最优解，但收敛速度慢，执行时间长，算法性能与初始值有关及参数敏感[16-18].粒子群算法虽然有较快逼近最优解的能力，但是由于所有粒子都向最优解的方向飞去，所有粒子趋于同一化(失去了多样性)使得后期收敛速度明显变慢，同时算法收敛到一定精度时，无法继续优化，所能达到的精度也不高.

针对以上问题，本文首先分析卫星任务规划在实际应用中的各种约束，建立具有一定通用性、可适用多种智能算法的问题模型.针对蚁群算法易陷入早熟以及模拟退火算法前期搜索速度较慢的问题提出了一种多星任务规划算法，利用蚁群算法对多星多任务分配问题进行前期搜索，在算法陷入停滞后利用模拟退火算法进行再搜索，提高了算法搜索效率及性能.

1 多星多任务分配问题建模

本文将任务分配问题描述为：在规定的调度时间内，将给定的卫星资源S在满足约束条件的情况下，合理地分配给任务集合I,并使得调度收益最大化.参数的定义如表1.

1.1 模型假设

由于卫星任务规划在实际问题中极为复杂，需要考虑的约束众多，卫星间的关系错综复杂，为了解决关键问题并不失一般性，对任务规划问题进行简化并作出如下合理假设：

1)每个任务只需要一颗卫星完成一次.

2)任务一旦执行，不可中断，直到完成.

3)因为卫星具有能量限制以及存储容量限制，任务在调度时间内安排时，需考虑是否满足卫星的资源限制.

4)卫星在同一时刻只能执行一个任务.

5)不考虑卫星发生故障的情况.

1.2 构建模型

卫星任务规划的目标为在调度时间内，在满足卫星约束的情况下，以尽可能少的资源完成尽可能多的任务，使得规划目标收益最大，因此多星任务规划是一个多目标问题[19-20].

表1 参数定义表Tab.1 Parameter definitions

(1)

(2)

rj=acj+bej

(3)

F=αF1-βF2

(4)

式中：F1是卫星观测的目标收益最大值；F2是卫星消耗能量最小值；F为综合优化值；xij为决策变量，xij=1表示任务j被卫星i所观测；a、b分别为完成一颗卫星观测任务需要消耗的能量和存储量的权重系数，数值可根据卫星自身的能量及存储量自行设置；系数α和β分别表示目标1和目标2的权重系数，具体设置可根据尽可能地观测到目标点，还是尽可能地节省资源自行设置.规划实现的最后结果是实现F最大.

1.3 主要约束条件

1)任务时间窗约束

xij(TBij,TFij)⊆xij(TSij,TEij),
∀i∈[1,NS],∀j∈[1,NT]

(5)

约束1表示任务的开始时间以及结束时间都得在时间窗内，其可见时间长度必须要大于任务的执行时长.

2)任务唯一执行约束

(TBij,TFij)∩(TBik,TFik)=φ

(6)

约束2表示任务唯一性约束，即卫星在同一时刻只能执行一个任务.任务i和任务k不可同时执行.

3)任务排他性约束

xij≤1

(7)

约束3表示任务排他性约束，即任务只需要完成一次即可.

4)原子性约束

xij(TFij-TBij)=xijdj

(8)

约束4表示任务的原子性约束，即任务一旦开始，必须执行，不可中断.

5)机动角度约束

v|TBij+1+TFij|≥|Angleij+1-Angleij|

(9)

约束5表示卫星的机动角约束，即上一个任务到下一个任务的时间乘以机动角速度大于等于2任务之间所需要的机动角度.

6)能量约束

(10)

约束6表示卫星的能量约束，即卫星i完成的所有任务消耗的能量小于等于卫星的总能量.

7)存储量约束

(11)

约束7表示卫星的存储量约束，即卫星i完成的所有任务存储容量之和小于等于卫星的总存储量.

2 多星协同任务规划算法

2.1 任务编码

本文提出了一种在卫星任务规划中的通用数字编码，适用于多种智能算法.具体编码规则为：根据任务数量Nt，设定等长的数字编码，编码上的每个元素定义为基因，每个基因有其相对应任务的编号.其基因的值为对应的时间窗口编号.任务的时间窗口与卫星相对应，确定了时间窗口编号，也就确定了此基因对应任务所选择的卫星编号.

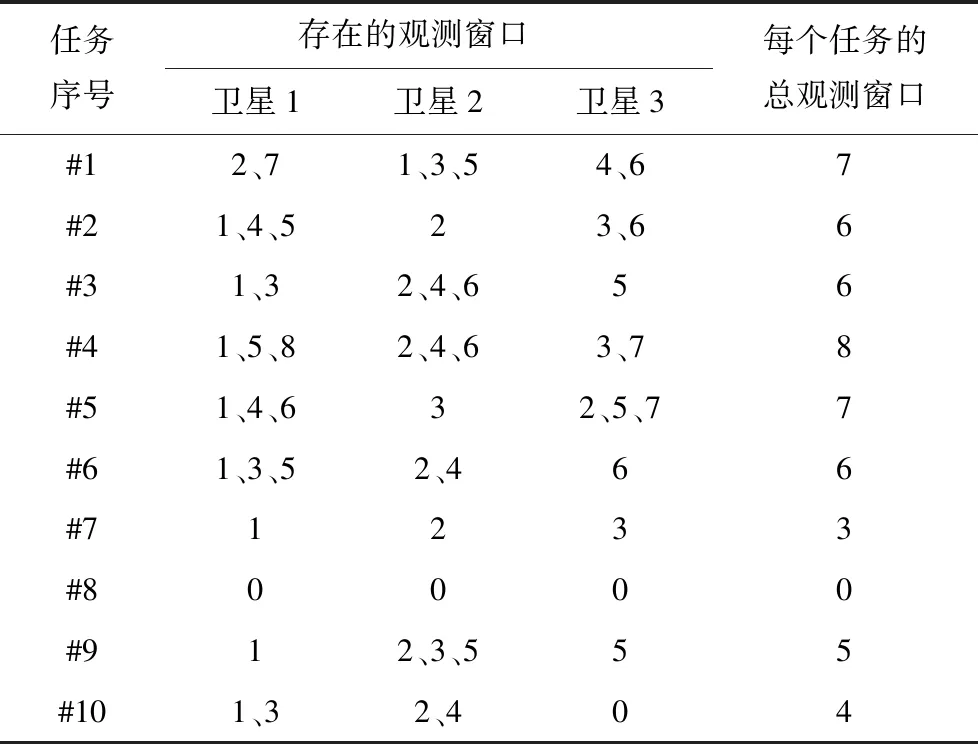
表2 多星多任务观测窗口Tab.2 Task observation windows for satellites

举例假设有3颗卫星、10个任务，假设在调度时间内卫星1对10个任务的总时间窗数目为2、3、2、3、3、3、1、0、1、2.卫星2对10个任务的总时间窗数目为3、1、3、3、1、2、1、0、3、2.卫星3对10个任务的总时间窗数目为2、2、1、2、3、1、1、0、2、0.卫星对任务的总时间窗口数目分别为7、6、6、8、7、6、3、0、5、4.具体窗口分布如表2.

图1表示任务可生成的一条初始解.以基因1、基因3和基因8为例，基因1上的取值为4，代表选择的观测窗口为第4个，由表1可知，由卫星3来进行观测；基因3的值为6，代表选择的时间窗口为6，即有卫星2执行观测；基因8取值为0，其代表的含义为由于所有卫星对此任务都没有时间窗口，因此此基因值只能为0.当然基因值不为0不代表这个任务肯定执行，还要通过时间窗约束规划窗口、机动约束规划窗口、资源约束窗口以及存储约束窗口进一步判断，上述规划都为长度为Nt的0-1二进制编码.0代表不满足此约束，1代表满足此约束，当任务j所对应的所有规划窗口都为1时，才代表任务j可以执行.

图1 任务编码表Fig.1 Task coding

图2 任务规划表Fig.2 Task schedule

规划窗口如图2所示，初始值全为1,1代表此任务执行，在后续的时间窗约束、机动约束、资源约束以及存储约束等条件下，有的任务规划窗会赋值0,0代表此任务不执行.

2.2 算法流程

本文将Ns×Nt的卫星合成观测问题分解为Nt个任务分配问题，其算法流程图如图3所示，即有Ns颗卫星，如何将Nt个任务在规定的调度时间内合理地分配给Ns颗卫星，在满足卫星约束的情况下，以尽可能少的资源完成尽可能多的任务，使得规划目标收益最大.

模拟退火算法具有局部搜索能力强但是前期搜索速度较慢的特点，蚁群算法虽然前期搜索速度较快，但是易陷入早熟停滞状态.针对以上特点，本文将蚁群算法经过迭代陷入停滞的结果作为模拟退火算法的初始解，然后采用模拟退火算法进行搜索，直到满足设定的终止条件，输出此时搜索到的最优解.

算法流程如下：

2)初始化信息素

(12)

3)构造状态转移矩阵Pik.本方法为增加收敛速度，增加了一个启发因子βik[12]，βik表示任务i的第k个时间窗口与其他时间窗口的重叠次数，βik越大表示若任务i选择第k个时间窗口，则与其他任务选择的时间窗重叠的可能性越高，造成任务收益完成情况也就越差.任务i选择第k个窗口的概率为

(13)

4)计算出任务i对所有窗口的概率后，按照轮盘赌算法对时间窗口进行选择，依次为每个任务选出一个时间窗口，构造出一条蚂蚁线路(完成所有任务的一个方案)，进一步依次遍历m只蚂蚁，为m只蚂蚁构造出相应的线路(构造出m个方案).

5)按照解的任务收益值大小从小到大进行排序，按照基本排序蚁群算法策略，蚂蚁按照它们的收益值大小进行排序，在每次循环中，只有排名在前ω位的蚂蚁才允许释放信息素.

6)信息素更新.信息素全局更新的目的是根据当前最优解的特征强化某些信息素，使其更有方向地进行收敛.选择一次迭代中的排名靠前的解更新信息素，更新规则如下：

τik(t+1)=ρτik(t)+ωrΔτ

(14)

式中：ρ表示遗忘因子；Δτ表示信息素增量；ωr表示排名靠前解的系数，排名越靠前，ωr值越大.

7)判断蚁群算法是否陷入停滞，若没有停滞则转3).当蚁群算法迭代一定次数后，由于信息素的不断更新，多个时间窗口之间的信息素差异过大，搜索容易陷入停滞.此时算法已经搜索到一个局部最优值.判断算法陷入停滞的条件为，带连续迭代ε1次，历史全局最优解仍然没有得到更新.

8)算法陷入停滞，输出当前全局最优解作为模拟退火算法的初始解进行搜索.

9)初始化模拟退火参数，不同于一般方式，初始温度T0不宜设置太高，而是选一个适中的值，既不会以较大的概率接受较差解，也不会完全不接受较差解.

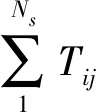
11)计算旧解与新解所对应的目标函数差ΔE(ΔE=Fn+1-Fn)其中F的定义详见式(4).

12)判断新解是否被接受.判断的依据是一个接受准则，最常用的接受准则是Metropolis准则:若ΔE>0则接受m1作为新的当前解m0，否则以概率exp(ΔT/T)接受m1作为新的当前解m0.

13)当新解被确定接受时，用新解代替当前解，这只需将当前解中对应于产生新解时的变换部分予以实现，同时修正目标函数值即可.此时，当前解实现了一次迭代.可在此基础上开始下一轮试验.而当新解被判定为舍弃时，则在原当前解的基础上继续下一轮试验.

14)降低当前温度，T1=T0q.其中q为降温系数.

15)判断当前迭代次数是否达到最终迭代次数，若不满足则转10)继续搜索，否则输出当前搜索到的全局最优解.

3 算法仿真

本文选取6颗卫星、200个观测目标.分别使用模拟退火算法、蚁群算法以及组合算法对多星多任务进行规划.200个观测目标的位置信息采用随机方式生成.每种算法分别迭代500次、1000次和2000次，对算法结果进行了比较.由于蚁群算法会很快陷入停滞，为了使蚁群算法能够继续搜索，本文在蚁群算法陷入停滞时采用信息素平滑的思想，具体实现方式为当算法陷入停滞时，将每个任务对应时间窗的信息素进行平均，使得任务选择所有时间窗的概率相等，以使得算法能够跳出局部最优解，实现再搜索.图4-6为3种不同算法的比较.

由仿真结果可以看出模拟退火算法的初始搜索速度较慢，而蚁群算法由于算法的正反馈特性，初始搜索速度很快，在较少的迭代次数就能达到一个较高值，远优于此时的模拟退火算法，而模拟退火算法的全局寻优能力强，在迭代次数达到1000次左右时，其解的质量已经基本上和蚁群算法持平，而当迭代次数达到2000次时，此时搜索到的全局最优解要优于蚁群算法.

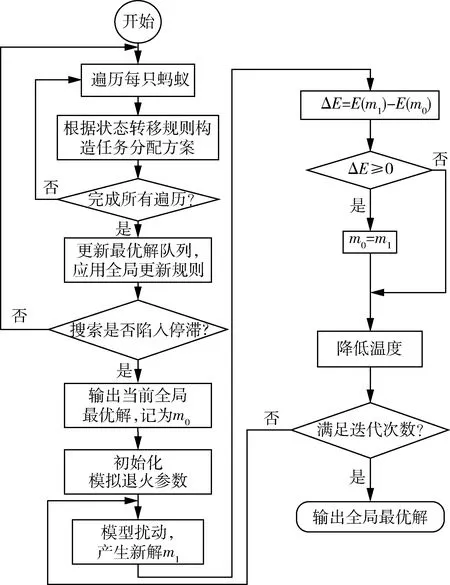
图3 多星协同任务规划算法流程图Fig.3 Flow chart of the multi-task planning algorithm for multi-satellite

图4 3种算法迭代600次的结果比较Fig.4 Comparison of 600 iterations of the three algorithms

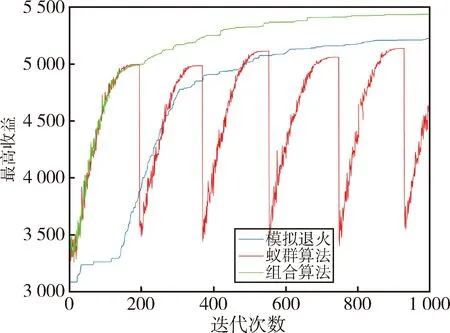
图5 3种算法迭代1000次的结果比较Fig.5 Comparison of 1000 iterations of the three algorithms

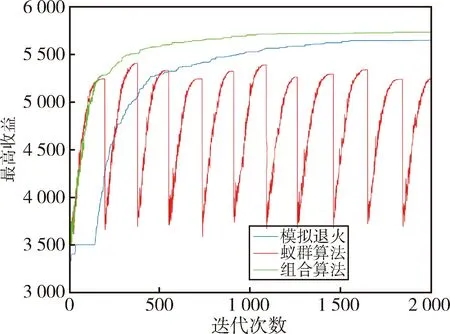
图6 3种算法迭代2000次的结果比较Fig.6 Comparison of 2000 iterations of the three algorithms

蚁群算法虽然可以很快地达到一个局部最优值，但由于自身算法的局限性，只能不断地更新信息素，进行再搜索，无法实现在这个局部最优值的基础上进行再搜索，不能保证每次搜到的解都优于上次.本文提出的组合算法前期利用蚁群算法，在较少的时间内就达到了一个局部最优值，此时利用模拟退火算法持续搜索全局最优解.相对于蚁群算法，组合算法可以在后期跳出局部最优，相对于模拟退火算法来说，组合算法可以在一个较高的起点进行搜索，避免了前期大量的无用搜索.通过结果对比，组合算法在不同迭代次数的情况下均优于模拟退火和蚁群算法，在迭代次数较少时，优势更为明显，可以在较短的时间内收敛到一个较好的结果.

4 结 论

根据多星任务规划问题提出了一种结合蚁群算法和模拟退火算法组合优化算法.首先对多星任务规划问题进行假设，并分析了多星任务规划问题中的多种约束，建立相应的数学模型，针对智能算法应用于多星任务规划问题中的编码问题，提出了一种数字编码方式，适用于多种智能算法，并在此基础上针对蚁群算法易陷入早熟以及模拟退火算法前期搜索速度的问题，提出了一种组合式多星协同任务规划算法，利用蚁群算法对多星任务规划问题进行前期搜索，在算法陷入停滞后利用模拟退火算法进行再搜索.最后进行了数字仿真分析，结果表明本文算法在不同的迭代次数下均优于蚁群算法以及模拟退火算法.