690合金U形传热管弯管残余应力数值模拟

2022-11-02施少波

化工机械 2022年5期

乐适罗垚施少波

（中核武汉核电运行技术股份有限公司）

镍基合金690在高温、高压环境中具有优良的耐应力腐蚀性能和良好的力学性能，因此广泛应用于压水堆核电厂的蒸汽发生器传热管中。传热管大多采用的是U形管，当传热管在冷弯过程中弯管区变形量超过弹性范围时，会出现塑性变形不均匀的现象，当卸掉外力矩后管子内部会残留保持自平衡的内应力。为了消减这种残余内应力，需要进行消应力热处理，此时材料又表现出粘弹塑性的特点，应力随时间变化，整个过程具有几何、材料和边界这3种非线性特点。最终的应力状态可能是复杂的，而残余拉应力又会引起材料应力腐蚀裂纹的萌生和加速扩展，最终导致材料破裂。美国电力研究院的蒸汽发生器降质数据库表明，由应力腐蚀引起的堵管占堵管总数的45%左右［1］。

近年来，国内外学者对管材弯曲成形做了大量的研究。艾治勇对钢管弯曲进行了应力理论分析，根据卸载回弹后内应力平衡和截面变形协调条件，建立了残余应力分布模型，然后采用有限元法对钢管弯曲进行了非线性模拟计算，验证了理论分析能够解决钢管弯曲中的各类力学问题［2］。宋彬等建立了数控弯管有限元模型，模拟了弯曲、抽芯和回弹3个过程，分析了应力应变分布规律，掌握了弯管成形与回弹的机理［3］。另一方面，关于消应力热处理的研究，国内外也有相关文献报道，王泽军采用有限元计算对球形储罐热处理后的残余应力消除效果进行了评价，认为残余应力的消除机制包括高温屈服和高温蠕变［4］。

690合金U形传热管已广泛应用于核电站蒸汽发生器中，但是对弯管之后残余应力的研究却很少。因此，笔者基于ANSYS Workbench有限元软件，模拟分析镍基合金690传热管的弯管、回弹、消应力热处理3个主要过程，从理论分析、数值模拟和试验测试3个方面对弯管区应力分布进行对比分析和验证，从而揭示管材弯曲成形和消应力热处理过程，为预测传热管的应力薄弱部位提供借鉴参考。

1 弯管成形理论分析

弯管成形在弯管机上进行，如图1所示。弯曲模绕圆心转动，夹模将管材夹紧并随着弯曲模转动特定角度，防皱模在管材内侧起支撑作用，压膜紧靠管材外侧，并以一定速度向前移动，芯棒对管材内壁起支撑作用。管子弯制完成后，将施加在管子上的所有外载卸掉使管子处于自由状态，此时管子会反方向回弹。回弹分为瞬时回弹和延时回弹：瞬时回弹是弹性应力释放导致的；延时回弹是材料内部原子结构重新排列和残余应力释放导致的，具有时间相关性，即随着时间的延长，回弹量增大，当增大到一定值后趋于稳定。

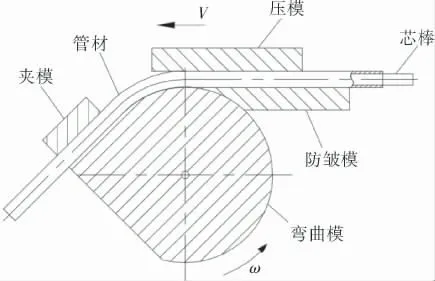
图1 弯管成形示意图

在分析瞬时回弹之前首先考虑管子弯曲时截面上的应力分布，管截面的弯曲应力理论基于两条基本假设：

其中，M为外力矩，I为截面惯性矩。

对于弹塑性模型，当外力矩M逐渐增大时，管截面上、下表面最先达到屈服，当继续增大M时，最外侧进入塑性，屈服面向中性层移动。

弯曲回弹残余应力σr通用表达式为：

其中，σ′为卸载过程中反向弯矩引起的回弹应力。

对于弹塑性强化弯曲残余应力，可表示为：

其中，σs为屈服强度，E为弹性模量，Eb为强化模量，εs为屈服应变，ρu为回弹半径，h为弹塑性临界线距离中性层的距离，R为管外半径。

根据应变关系式ε=εu+εr（其中εu为回弹应变，εr为残余应变），并结合平面假设可得到：

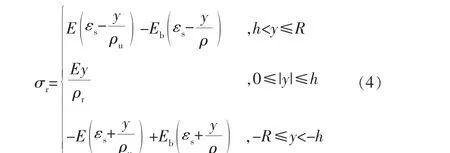
其中，ρr为残余半径。

根据式（4）绘制弯曲残余应力分布图（图2）。

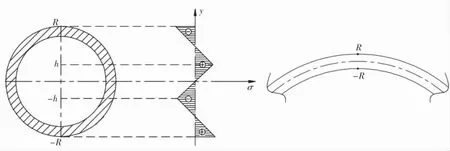
图2 弯曲残余应力分布

残余应力内部平衡满足截面上静力矩之和为零，即：

其中，A为横截面面积。

因为E≫Eb，所以管子最外侧（R点）残余应力可近似表示为：

其中，λ=r/R。

2 消应力热处理

690合金管材在弯制成型后要进行整体消应力热处理以降低管子内部的残余应力。

采用消应力热处理工艺实际上是加速了延时回弹趋于稳定的时间，在这个过程中伴随着应力松弛。采用蠕变本构模型来分析延时回弹过程。

690合金传热管消应力热处理的温度超过700 ℃，根据文献［5］的蠕变试验数据，蠕变速率基本恒定，对于这种稳态蠕变，采用Norton幂率本构模型来描述：

其中，·εcr为蠕变应变率，σ为等效应力，C1、C2、C3为常数，T为绝对温度，e为自然常数。

对Norton方程中的参数进行拟合，拟合曲线如图3所示，拟合参数见表1。

图3 蠕变参数拟合曲线

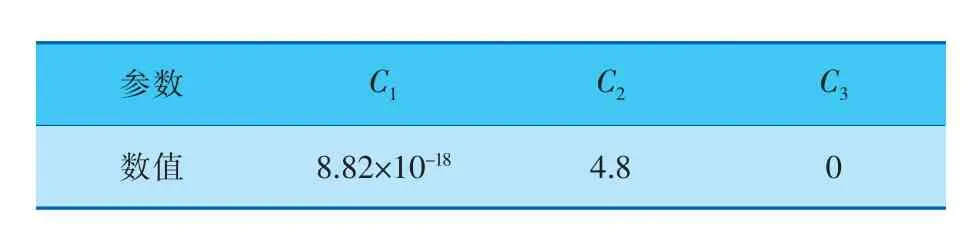
表1 Norton蠕变模型的材料参数

3 有限元模型

以690合金传热管为研究对象，弯管成形角为180°。根据690合金管材单轴拉伸试验数据，采用弹塑性强化模型，参数见表2。

表2 材料弹塑性参数

管子有限元模型如图4所示，由于该模型涉及材料非线性、边界非线性（接触计算）和几何非线性（大变形），是高度非线性问题，为了提高收敛性，降低计算量，将模具都假设为刚体，在计算中不考虑它们的形变。管子采用三维实体网格Solid185单元，弯曲载荷通过模具与管子的接触力传递，因此本模型的关键是接触对的设置，共有5处接触对，见表3。接触算法采用纯罚函数法，接触刚度系数为0.1。弯管及后续的热处理可以看作是准静态过程，因此采用静力分析，打开大变形效应。

表3 接触对和摩擦系数

图4 管子有限元模型

4 边界条件及载荷施加

边界条件设置及载荷施加步骤如下：

a. 压模、芯棒和防皱模固定约束；

b. 在室温下，夹模和弯曲模绕弯曲模轴心转动189°（考虑回弹角度）；

c. 夹模复位卸载，管子在自由状态下回弹；

d. 按照消应力热处理工艺时间-温度曲线（图5）施加温度载荷，此过程同时考虑蠕变应力松弛和热弹塑性应力应变。

图5 消应力热处理工艺时间-温度曲线

5 计算结果分析

在分析结果之前有几点需要说明：

a. 根据弯曲应力理论假设条件，弯曲成形过程主要由轴向应力与应变决定，因此主要分析其轴向残余应力。

b. 试验采用X射线衍射法对管子表面残余应力进行测量，在弯管区选择0、45、90°3个截面，每个截面沿环向选择4个点，分别是a点（外侧）、b点（上部）、c点（内侧）和d点（下部），如图6所示。对每个位置上4个点的轴向残余应力进行测量。有限元后处理也是在相同位置取值与试验值进行对比。

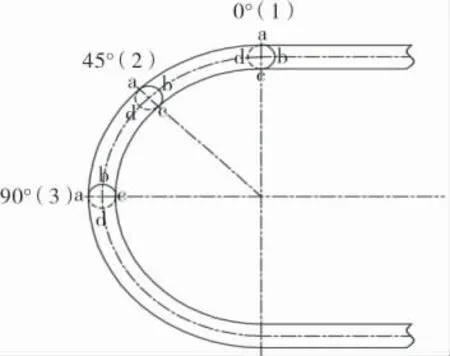
图6 弯管区不同部位残余应力检测示意图

c. 从残余应力的危害来说，一般残余拉应力会引起材料应力腐蚀裂纹的萌生和加速扩展，因此重点关注残余拉应力的分布。

5.1 弯管成形后（消应力前）

图7为管子回弹前后的变形情况。图8比较了管子回弹前后截面的轴向应力变化情况。可以看出，在弯管回弹前由于有夹模的约束，管子外侧保持拉应力，内侧保持压应力。拉应力最大为350 MPa，压应力最大为391 MPa，外层和内层的应力方向相反、大小相近，符合弯曲截面应力分布理论。在中性层附近应力基本成线性分布，与式（1）相符，在远离中性层位置出现拐点，拐点之后的应力变化幅度不大，这主要是因为强化模量远小于弹性模量，说明材料已进入塑性阶段。

图7 管子回弹前后的变形情况

图8 弯管回弹前后管截面的轴向应力变化情况

卸载后，管子为了恢复部分弹性形变而发生回弹，外层和内层的应力变化幅度是最大的，管子外层由原来的拉应力变为压应力，内层由原来的压应力变为拉应力，在中性层附近出现最大拉应力和最大压应力，图8数值计算结果与图2的理论分析相吻合。

5.2 消应力后

按照图6所示的截面提取管子消应力后轴向残余应力，如图9所示。图9中，管外侧（a点）均为最大压应力，管内侧（c点）均为最大拉应力。有限元计算结果与试验结果对比见表4，可以看出二者应力变化趋势相符。

图9 外侧和内侧轴向残余应力随回弹角度的变化

表4 结果对比

根据文献［6］，通过对奥氏体不锈钢进行沸腾氯化镁试验表明，裂纹一般出现在残余应力超过100 MPa±20 MPa的试样表面，而690合金抗应力腐蚀能力优于奥氏体不锈钢，因此可以认为通过消应力热处理后残余拉应力水平是偏低的。

由于试验只测得了管子表面4个间断位置（0、90、180、270°）的残余应力，为了分析管壁截面内残余应力的连续变化趋势，找到残余应力的最大部位，通过有限元计算方法，取横截面上0～180°的圆弧，沿管壁厚度提取内层、中层和外层上的轴向残余拉应力，如图10所示。综合来看，外层（即管子外壁面）80°附近残余拉应力是最大的。