基于球形标靶的激光扫描仪位姿测量技术

万海霞 马慧卿 王 真

中交水运规划设计院有限公司

1 引言

3D激光扫描仪通过向外部发射和接收激光束来获得物体表面的点云数据，进行物体的3D重构，在高精度3D地形构建、三维重建及变形监测等领域得到了十分广泛的应用[1]。在3D重建领域通常采用多个标定球完成不同坐标系下点云数据的匹配，实现坐标系之间的相互转换。为了得到扫描对象的完整点云数据，通常需要在多个不同角度扫描测量目标，由于在不同的位置扫描中三维激光位置发生变化，需要根据位置传感器反馈结果来估算不同测量站的相对位姿，将得到的点云数据转换到全局坐标系下[2-3]。由于标定球每个方向上的球心点是固定的，并且是唯一的，所以在匹配时通常采用3个以上标定球来进行[4]，如果要扫描的目标周围有干扰源以及扫描的目标点云本身含有密集噪声，会对最终的匹配精度有很大的影响。

目前点云数据匹配算法的研究很多，但标定目标在扫描后包含误差的情况常被忽略[5]。最小二乘法是最常用的球心拟合算法，但是没有充分考虑扫描时目标本身的点云中含有粗糙度和噪声的情况，采用最小二乘解算时噪声对球心的计算结果有很大的影响。因此本研究在对球心计算前首先对球面周围的离散噪声进行滤波，基于去除噪声后的点云数据对球心坐标进行拟合，并将最终计算结果作为匹配的关联点。现场测试证明，本系统在保证作业安全的同时，还具有控制精度高、稳定性强、实时性好的特点。

2 基本原理

根据点云配准的基本原理，想要求解同一个斗轮堆取料机在不同时刻的位姿变换，至少需要3个不共线的公共点。实际上扫描仪很难在料场中获取不同时刻下的公共点。近年来一些文献采用单个或者多个球形标靶对激光或相机进行内参和外参的标定工作[7-8]，本研究采用4个标准球形标靶进行标定(见图1)。

图1 标定球现场布置示意图

2.1 坐标系建立

为了求解坐标系之间的转换关系，需要根据堆取料机的的运动机构构建各个机构的坐标系，最终能使数据还原到全局坐标系下。子坐标系包括：激光扫描仪坐标系Claser；俯仰机构坐标系Cpitch；回转机构坐标系Cyaw和轨道坐标系Crail(见图2)。坐标系之间的变换关系是由旋转矩阵和平移矩阵两部分组成，这两部分为主要的标定参数，设备在运动过程中的位姿数据利用设备自身的传感器系统获得，包括行进距离、回转角度、俯仰角度，将位置反馈值和扫描数据组合起来进行标定。

图2 各坐标系的建立

2.2 建立球心拟合模型

扫描仪在不同位姿(不同回转角度、俯仰角度)下扫描球形标靶的表面，若标定球附近存在其他物体的干扰，或扫描标定球表面时点云含有大量噪声，则会对拟合出来的球心坐标产生较大的偏差，并对点云匹配的精度产生较大的影响。所以需要对激光扫描仪获取的点云数据去除冗余点和噪声点，同时已知标定球的制造半径，现场各个球之间的相对距离、球心到水平面的距离以及现场标定球大致的摆放位置等为约束条件，从扫描到的点云数据中分离出标定球的点云数据，分离结果见图3。

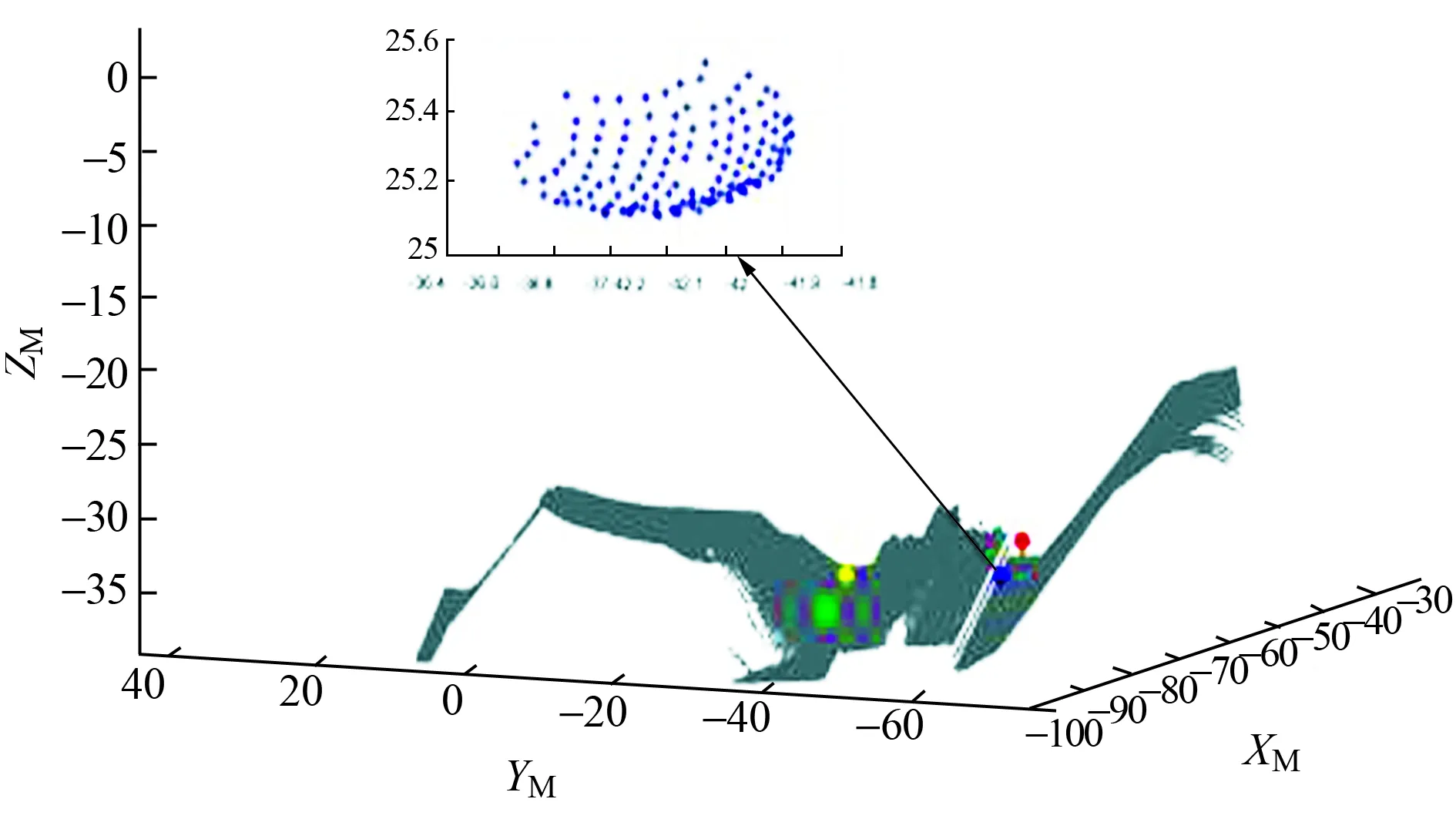
图3 球体表面特征点提取

三维球面球心的求取，至少需要采集球面上4个不同点的扫描数据方可计算出球心坐标。设拟合的球心坐标为(x0，y0，z0)，半径为r，采用最小二乘法对分离出的标定球表面点云数据进行拟合，此方法能以更高的精度对球心进行拟合，球的方程如下。

(xi-x0)2+(yi-y0)2+(zi-z0)2=r2

(1)

式中，xi、yi、zi为采集的球体表面坐标值；x0、y0、z0为球心坐标的最小二乘估值；r为球半径。式(1)是一个关于a、b、c的非线性方程组。已知球表面任意2点(xi,yi,zi)和(xi+1,yi+1,zi+1)满足：

(xi-x0)2+(yi-y0)2+(zi-z0)2

=(xi+1-x0)2+(yi+1-y0)2+(zi+1-z0)2

(2)

对式(2)展开可得：

基于交通载荷作用下顶管顶力计算优化分析………………………………………王晓凡，张玉廷，白延杰（6.37）

(3)

v=Ax-L

(4)

基于最小二乘原理可以拟合出球心坐标X(x0,y0,z0)的估值：

X=(AT×A)-1×AT×L

(5)

现场标定时使堆取料机在多个位置下采集标定球的表面数据，根据分离出的标定球表面数据求解各标定球的球心坐标。现场在40组不同位置下求解出各标定球的球心坐标，表1中列出了部分数据。

表1 球心坐标计算

2.3 建立标定参数模型

采用Rodrigues罗德里格斯公式将旋转矩阵R表示为R(k,θ)，k为旋转轴，θ为相应部件的运动角度值，式(6)表示球形靶标球心坐标值从激光扫描坐标系到局部料场坐标系下的坐标值，其中Cij表示局部料场坐标系下球形靶标的球心坐标值，t1、t2、t3为矩阵的平移量，k1为回转轴，k2为俯仰轴，k3为激光与设备安装位置的固有偏差,μi,j为设备在第i个位置下扫描仪坐标系下第j个球的坐标值[9-10]。

Cij=

(6)

对式(6)展开可得：

Ci,j=R1,j[R2,j(R3,jμi,j+t3)+t2]+t1

(7)

假定标定中4个标准球的测量是等精度的，全局标定最终表示为求解式(8)所示的优化问题，通过高斯牛顿(Gauss-Newton)、列文伯格-马夸尔特(LM)算法可以对相关参数进行优化求解。

Fi,j(θ1,θ2,θ3,k1,k2,k3,t1,t2,t3)

(8)

计算Fi,j关于k1、k2、k3的导数为：

(9)

计算Fi,j关于t1、t2、t3的公式为：

(10)

构造矩阵式为：

(11)

并有

bi,j=-Fi,j

(12)

构建X的估计表达式：

X=(AT×A)-1×AT×T

(13)

全局标定包含3组刚体变换参数的求解，因此需至少3个不同的大机位姿才能完成标定，且姿态的变化不可在同一平面内，标定球全局坐标系下的坐标见表2。

表2 标定球全局坐标值

2.4 测试结果

对40组描仪坐标系下标定球球心数据与姿态数据，结合全站仪所测量的全局坐标系下目标球形靶标的坐标值，采用LM算法进行参数优化求解其结果见表3。利用激光扫描仪在不同的位置对同一料堆进行扫描，对标定参数和设备当前姿态数据进行数据配准，在最远距离100 m处，点云的变换后的误差可以控制在100 mm以内。

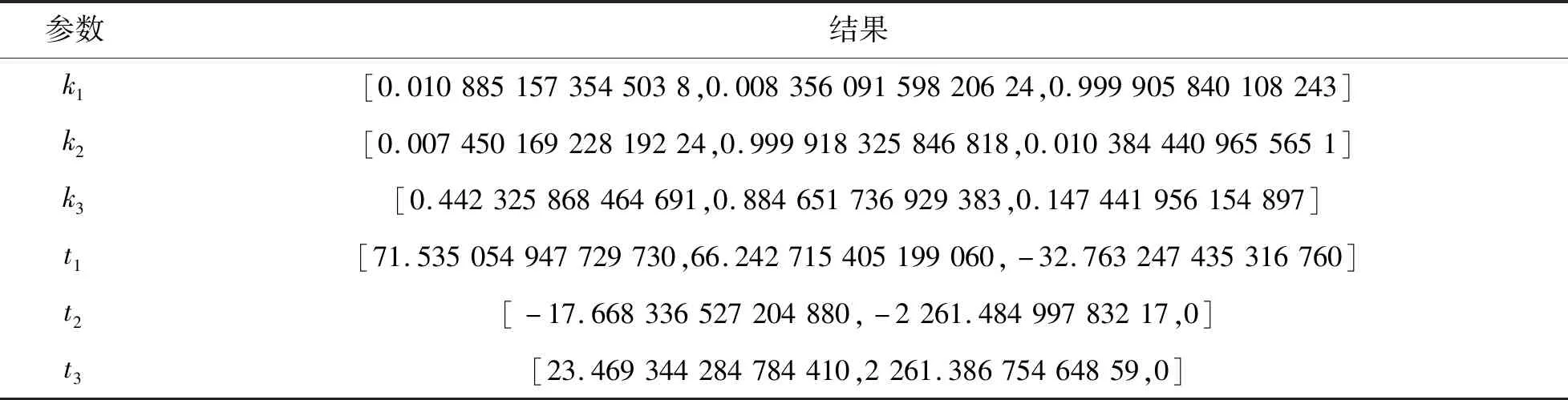
表3 标定结果

3 结语

针对三维激光扫描仪姿态测量模型参数估算，采用基于球形标靶的姿态模型参数估算方法，将球形靶标的已知特性作为约束条件，对球形标靶表面点云数据进行分离，筛选出有用的点进行球心求解；通过最小二乘对筛选后的点云进行拟合，发现半径解算的结果基本与标定球的制造参数一致，偏差控制在±10 mm。同时以此球心解算结果作为设备在不同位姿下的公共点，并且联合设备位置数据采用LM优化算法最小化目标函数，完成全局标定参数估算，对解算的结果进行反推和多次的现场测量，在多个位姿下将目标料堆三维数据变换到料场坐标系下误差可控制在100 mm以内，该标定结果能满足堆取料机无人化控制要求。