基于振动声学的变压器健康状况评估方法研究
2022-11-02王树东吴永勇刘春艳
王树东, 吴永勇, 刘春艳
(1.兰州理工大学 电气工程与信息工程学院,甘肃 兰州 730050;2.甘肃省工业过程先进控制重点实验室,甘肃 兰州 730050;3.青海大学 水利电力学院,青海 西宁 810016)
0 引 言
电力变压器健康稳定运行在电力系统中重要性不言而喻[1]。近年来,分析电力变压器振动信号为评估变压器内部健康状况以及电力变压器本体的机械状态提供了一种可行的方法。电力变压器的机械应力或位移的变化可以通过分析和监测所产生的振动频率来获得,这对持续监测其内部机械稳定性和确保其电气和机械部件的完整性有很大帮助。
目前,通过电力变压器振动信号分析对研究电力变压器内部机械稳定被国内外研究人员所认可并对此进行了深入研究。文献[2]主要研究负载电流、电压和油温与电力变压器振动产生的关系,并将绕组的固有振动频率作为变压器诊断的重要指标。文献[3]通过振动信号分别对电力变压器铁心和绕组故障做了研究,对精确诊断电力变压器内部故障有重要意义。
运行环境的复杂使得电力变压器振动受多因素影响。正常的电压波动也会引起铁心振动[4],电力变压器本体的冷却系统也会使其振动并且监测所得电力变压器振动信号中会包含环境噪音。针对以上问题,本文在考虑上述因素的前提下研究了希尔伯特-黄变换(Hilbert-Huang transform,HHT)在基于振动信号的电力变压器健康状态评估方面的优越性,并进行了试验验证。
1 电力变压器振动机理分析
电力变压器振动声源主要由铁芯、绕组以及空载、负载和冷却系统所引起[5]。电力变压器内部振动声源产生机理如图1所示。

图1 变压器振动产生原理图
1.1 电力变压器铁心振动机理分析
电力变压器的铁心通常由硅钢制成,电力变压器内部的交变磁场使得硅钢片发生磁致伸缩效应[6]。因此,励磁频率的变化导致电力变压器铁心产生振动。图2为不同应力下的磁致伸缩曲线。从图2可以看出,硅钢片的磁致伸缩效应随着电力变压器内部的机械紧密程度变小而增大。
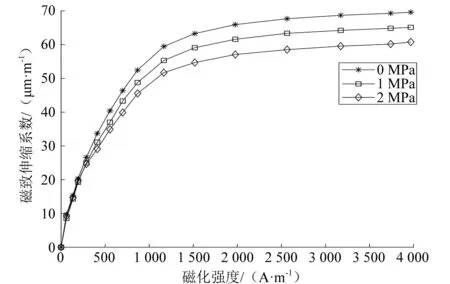
图2 硅钢片在不同应力下的磁致伸缩曲线
电力变压器磁场求解可用有限元分析法[7],引入磁势矢量因子Aθ,问题转化为求解边界值问题。Aθ满足的泊松边值方程为:
(1)
式中:Ω为求解区域;Jsθ为电流密度Js的分量;Γ1、Γ2为两种边界条件;Ht为其切向量;T0为初始时刻。式(1)基于变分函数,经离散化处理后可以求出磁势矢量值Aθ。故电力变压器铁心轴向漏磁分量和径向漏磁分量分为:
(2)
由式(2)得磁感应强度矢量为:
(3)
由式(3)以及Maxwell’s equations可知,电力变压器铁心所受的电磁力[8]可表示为:
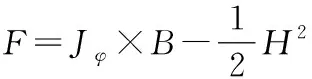
(4)
式中:Jφ为电流密度;H为磁场强度;μ为介质的磁导率;τ为介质的体积密度。式(4)中的第一项为洛仑兹力;第二项为材料体积力;第三项为材料表面张力。
1.2 电力变压器绕组振动机理分析
电力变压器绕组振动主要原因是绕组线圈在漏磁场中受到电磁力以此造成了绕组的振动[9]。
根据Biot-Savart定理和变压器绕组中的电流关系可得到绕组所受洛伦兹力以及任一位置绕组所受洛伦兹力的时域表达式为:
(5)
式中:J为电流密度;B为磁感应强度;Kb为比例系数;Im为电流密度幅值;ω为电源的角频率;φ为电流的初相角。
2 HHT理论
HHT是一个处理非平稳信号的理想工具[10]。经验模态分解(empirical mode decomposition,EMD))和Hilbert变换(Hilbert transform,HT)是HHT的两个重要组成部分。EMD用于分解信号是HHT分析的第一步。EMD根据信号的本征特征尺度生成固有模态函数(intrinsic mode function,IMF)),IMF是EMD的重要组成部分。第二步是HT,它将瞬时频率转换为时频能量分布,以方便对信号进行分析。
2.1 EMD理论
经验模态分解是一种多分辨率分解方法,它将非平稳信号分解成许多源于被分析信号本身的IMF[11]。但IMF必须满足两个条件。
(1) 整个信号内,极值点和过零点的数量相差≤1。
(2) 任意时刻,由局部极点定义上、下包络线之间的平均值为零。
对于原始信号x(t)进行EMD分解的具体实现过程如下:
(1) 找出x(t)所有的局部最大值和最小值,然后用三次样条拟合出上包络线xmax(t)和下包络线xmin(t)。
(2) 计上、下包络线平均值记均值为m1(t):
(6)
(3) 计与原始信号的差值,得到第一个分量h1(t):
h1(t)=x(t)-m1(t)
(7)
(4) 判断结果h1(t)是否符合IMF的两个条件。如果符合,记c1(t)=h1(t),c1(t)为第一个IMF成分。否则,将h1(t)视为新的信号,并通过步骤(1)~(4)对h1(t)进行迭代。
(5) 通过k次迭代,信号与定义为h1k(t)的平均包络之间的差值:
h1k=h(k-1)(t) -m1k(t)
(8)
式中:m1k(t)为k次迭代后包络的平均值;h1(k-1)(t)为信号和迭代平均值之间的差值。如果h1k(t)满足IMF分量,记c1(t)=h1k(t)。
(6) 残基表示为:
r1(t)=x(t)-c1(t)
(9)
r1(t)可被视为一个新信号,并根据步骤(1)~(5)重复迭代以获得其他IMF,得到ci(t)和一个残基ri(t)。
ri(t)=r(i-1)(t)-ci(t),i=1,2,…,n
(10)
当ri(t)为单调函数时分解停止。于是,原信号x(t)可以写成
(11)
式中:ci(t)为全部固有模态函数IMF;ri(t)为信号分解的余数。
考虑实际情况多数信号并不能满足IMF的两个条件[12]。为此,Norden E.Huang提用h1(k-1)和h1k(t)的标准差Sd来判断小循环筛分过程是否可以停止。即迭代停止条件必须被视为:
(12)
2.2 Hilbert理论
HT[13]是由时域到时域的变换。在HHT当中的具体实现过程是通过EMD获得每个IMF成分ci(t)。对ci(t)进行HT可得:
(13)
HHT基于瞬时频率计算[14]。通常,实部x(t)和虚部y(t)的和可表示所有的解析信号。故将振动信号构造为式(14)的等式,其中:a(t)为瞬时幅度;θ(t)为瞬时相位。因此,HT表示为:
z(t)=c(t)+jy(t)=a(t)eiθ(t)
(14)
(15)
HT对于原信号x(t)瞬时频率的特征表达式:
(16)
HT变换得到的振幅和频率都是以时间为变量的函数,式(14)中所示的分析信号的实部可以表示信号x(t)Hilbert时频谱即:
(17)
从式(17)可以看出,非平稳信号x(t)仍可以分解成多个IMF分量,根据EMD分解,通过单个分量的IMF的HT得到信号中包含的瞬时特性。综上,x(t)的Hilbert频谱表达式如下:
(18)
式中:HHTi(t,f)为时间-频率分布函数;ai(t,fi)为IMF分量的振幅ai(t)和瞬时频率fi(t)组成的函数。它侧重于频率成分和信号能量的时间相关性。同时根据Huang的定义,还能得到Hilbert边际谱的定义:

(19)
上述公式表明,Hilbert频谱在高频谱分析中代表了瞬时振幅和瞬时频率的特点,而Hilbert边际频谱则给出了信号中积累的各种频率的振幅,其时间可以通过HHT谱来定位。
3 试验与分析
3.1 振动试验
为验证HHT在电力变压器振动信号分析中的优越效果,通过传感器采集电力变压器进行振动信号并进行HHT分析。原始信号的可视化分析如图3所示。图3为采集得到的振动信号时域波形,对采集的原始数据进行HHT变换分析可以得到EMD分解结果以及对应的频谱图。
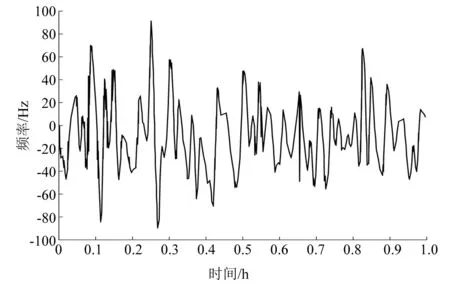
图3 原始振动信号图
3.2 结果分析
对所采集的原始振动信号进行HHT分析得到如图4所示的EMD分解图与对应频谱图。从图4可以看出,原始信号通过EMD分解成五个IMF成分和一个残余量。IMF描述了信号的内在的振动模式。其中IMF1频谱的分布没有明显的规律性,能量分布范围为0~300 Hz。由本文第一节的分析可得IMF1主要为环境噪声或干扰信号元素。IMF2和IMF3的频谱明显地集中在50~100 Hz,这表明了EMD分解具有很好的自适应选频特性。
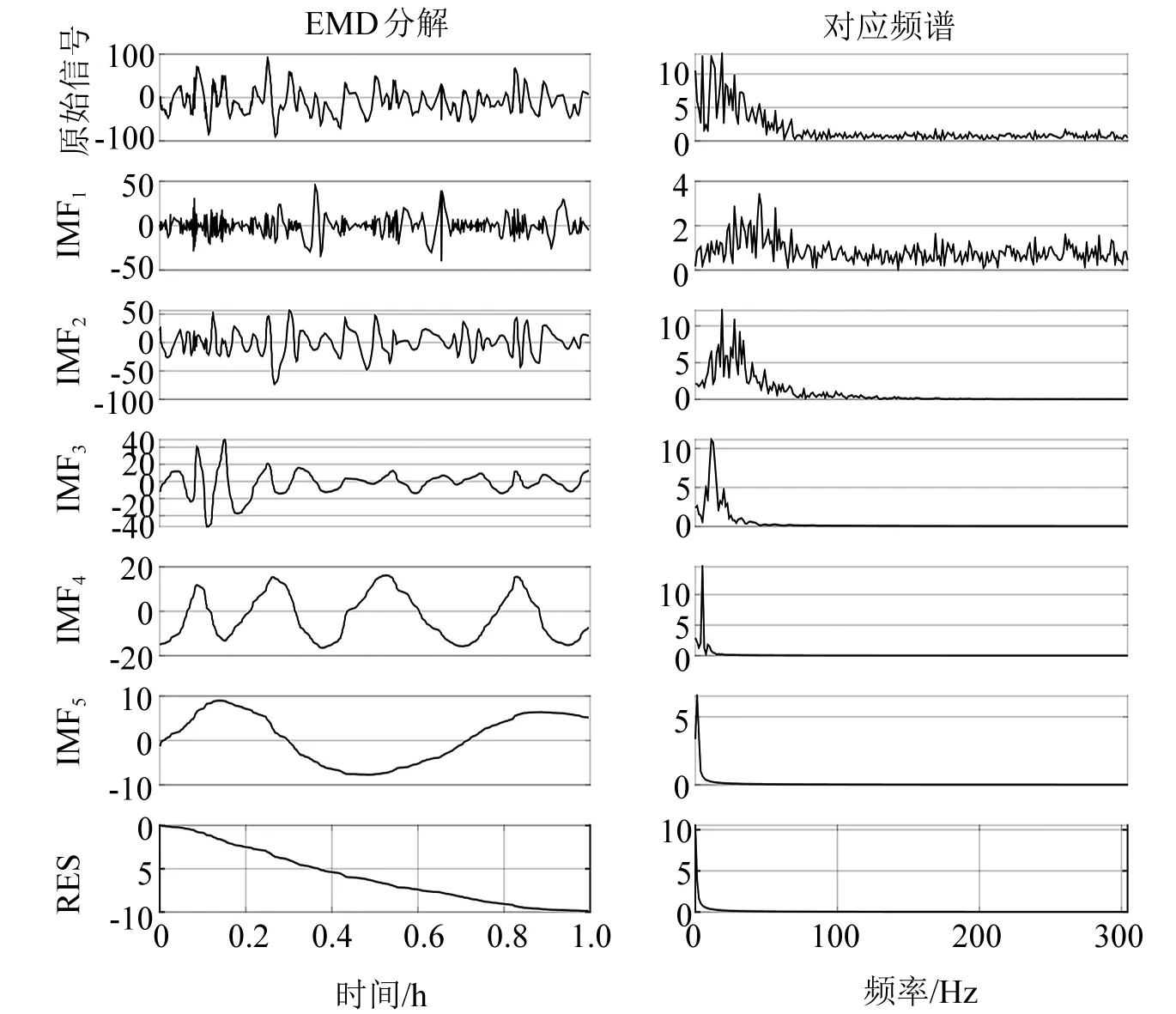
图4 EMD分解图与对应频谱图
从IMF2和IMF3的形态和频谱可以看出,变压器该点处的振动主要由50~100 Hz的频率构成。电力变压器绕组振动的频率是交流电频率的2倍。故此从IMF2和IMF3的形态和频谱可以得知,在所采集的振动原始信号时间段内,变压器的异常振动主要是由电力变压器铁心故障引起。IMF4和IMF5并无明显变化规律,频率处于低频段范围内。从变压器振动的原理来看,小频率分量不是由电磁变化引起的,而是由外部影响引起的。
4 结束语
本文分析了变压器铁芯和绕组振动的原因,提出了通过振动信号分析来评估变压器内部健康状况,并提出利用HHT分析方法对电力变压器振动声学信号进行分析。结果表明,利用振动信号来评估变压器内部健康状况解决了变压器内部健康状况无法直观获得和无法带电评估的问题。利用HHT法分析变压器内部铁心以及绕组振动信号,根据EMD分解图和相应的频谱图,可以直观、准确地判断出变压器的健康状况,以及造成电力变压器内部故障的原因。综上所述,利用振动声学分析方法来评估变压器内部健康状态是一种高效、可带电且非破坏性的分析方法,有一定的应用前景。
