基于随机森林和双向长短期记忆网络的超短期负荷预测研究
2022-11-02伍乙杰黄文灏赖仕达陈光宇贾鹏李家兴
伍乙杰, 黄文灏, 赖仕达, 陈光宇, 贾鹏, 李家兴
(1.南京工程学院 电力工程学院,江苏 南京 211167;2.国网福建省电力有限公司三明供电公司,福建 三明 353000)
0 引 言
实现供电量与电力负荷的动态平衡是电力系统稳定经济运行的前提,而负荷具有较强的波动性和非线性,且随着数据采集系统的发展,负荷信息呈现多特征的特点,增加了预测的难度。因此,挖掘负荷与特征因素的内在关联,降低输入变量的维度,对准确预测负荷具有重大意义。
负荷预测主要有传统预测法和神经网络法[1]两类。文献[2]针对短期负荷预测精度差的问题,利用传递函数对累积式自回归动平均(autoregressive integrated moving average model,ARIMA)进行改进,仿真结果表明改进后的模型提高了预测精度。文献[3]提出了将猫群算法和误差反向传播(back propagation,BP)神经网络相结合的负荷预测模型,有效提高具有天气特征的负荷预测精度。文献[4]采用长短期记忆(long-short-term memory, LSTM)网络,并考虑电价对负荷的影响,负荷预测精度相比于传统预测模型提升很大。上述文献对单一特征影响下的负荷预测进行了深入的研究,有效地降低了预测误差。然而,上述方法无法有效处理高维时间序列信息,其模型训练耗费时间长且预测精度较低。
针对上述问题,提出了一种基于随机森林和双向长短期记忆(bi-directional long-short-term memory, Bi-LSTM)[5]网络的超短期负荷预测方法。首先,采用基于随机森林的特征选择算法,筛选与负荷关联性强的输入特征,降低输入预测模型数据的维度;其次,构建Bi-LSTM网络,对特征选择后的负荷数据进行预测;最后,采用某市真实负荷数据进行仿真分析,并与其他传统网络对比,结果表明所提方法在负荷预测方面具有较好的性能。
1 基于随机森林的特征选择
随机森林(random forests, RF)[6]是由多棵决策树集成的有监督的学习算法,在决策树的训练过程中随机选择特征,最终通过投票来表决最优结果。随机森林原理图如图1所示。

图1 随机森林原理图
假设训练集有M个样本,有放回地抽取m个样本得到采样集,未被抽取的样本称为袋外数据(out of bag, OOB)。在回归树分裂生成随机森林过程中,依据方差最小准则选择分裂变量。回归树向最优方向完成生长,形成包含N棵树的随机森林,并可通过计算袋外数据误差来达到对特征选择的目的。其具体步骤如下:
步骤1:计算每棵决策树袋外数据误差EiOOB1。
步骤2:只对袋外数据第j列(第j个负荷特征)引入噪声干扰,重新计算袋外数据误差值EiOOB2。
步骤3:若随机森林有N棵决策树,则第j个特征重要性得分的计算公式如下:
(1)
步骤4:计算所有特征重要性得分并降序排列,可筛选出与负荷关联性强的特征。
2 Bi-LSTM网络模型
LSTM网络通过遗忘门、输入门和输出门来实现信息的保护和控制,有效避免了梯度消失,其单元结构如图2所示。
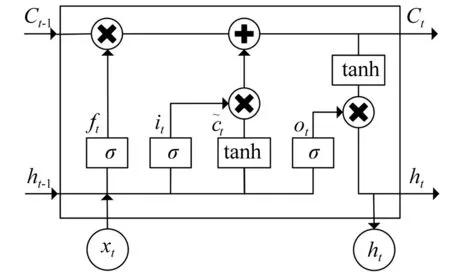
图2 LSTM单元结构图
遗忘门计算公式:
ft=σ(Wfxt+Ufht-1+bf)
(2)
输入门计算公式:
it=σ(Wixt+Uiht-1+bi)
(3)
(4)
更新记忆细胞:
(5)
输出门计算公式:
ot=σ(Woxt+Uoht-1+bo)
(6)
ht=ot⊙tanh(ct)
(7)
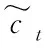
Bi-LSTM由向正反两个方向传递且共享权值的LSTM网络组成,可从正反2个方向学习时间序列,结合序列的历史信息和未来信息,具有很强的表达能力,其结构图如图3所示。
图3 Bi-LSTM结构图
3 负荷预测模型
负荷信息的本质是一种多维时间序列,主要受温度、天气和节假日等因素的影响。将原始负荷数据直接作为Bi-LSTM网络的输入,训练效率较低且容易欠拟合。本文采用基于随机森林的特征选择算法对负荷的特征数据进行筛选,删去无关特征量,提高预测精确度,具体步骤如下:
步骤1:输入负荷数据集。负荷数据集构成输入向量{yload,x1,x2,…,xn}。
步骤2:数据归一化[7]。为加快模型训练的速度,对输入数据进行归一化处理,将其映射到[0,1]范围内,具体表现形式如式(8)所示。
(8)
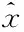
步骤3:基于随机森林的特征选择。决策树数量以及最大深度是影响随机森林性能的主要参数,使用网格搜索算法[8]来确定决策树数量为110,最大深度为20。将归一化的数据作为随机森林的输入,计算所有特征的重要性得分并降序排列,选择与负荷关联性强的特征向量。
步骤4:基于Bi-LSTM网络的负荷预测。将特征选择后的数据输入Bi-LSTM网络中进行训练,模型训练完成后,对测试集数据进行预测。采用均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)作为模型评价指标,其公式如下:
(9)
(10)
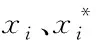
4 算例分析
算例数据选取某市10个月的电力负荷数据,采样频率为15 min,包含28 276个样本,前8个月数据为训练集,后2个月数据作为测试集。负荷数据包括每日气温、时刻和节假日等13个负荷影响因素,具体特征如表1所示。

表1 负荷特征描述
首先,对负荷数据进行归一化,将实际负荷作为标签值,其余负荷相关数据作为输入变量,采用随机森林算法进行预测,并可视化各特征的重要性得分,其可视化结果如图4所示。
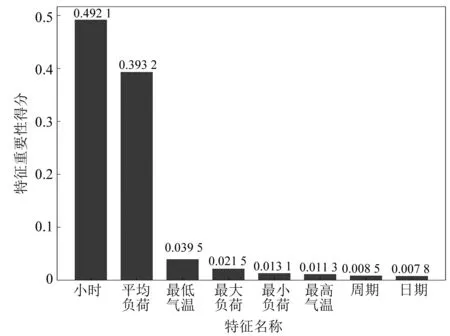
图4 特征重要性得分
图4给出了重要性得分在前8位的特征,构建两层Bi-LSTM网络,迭代次数为10,研究剩余特征个数对预测精度的影响,预测误差如图5所示。
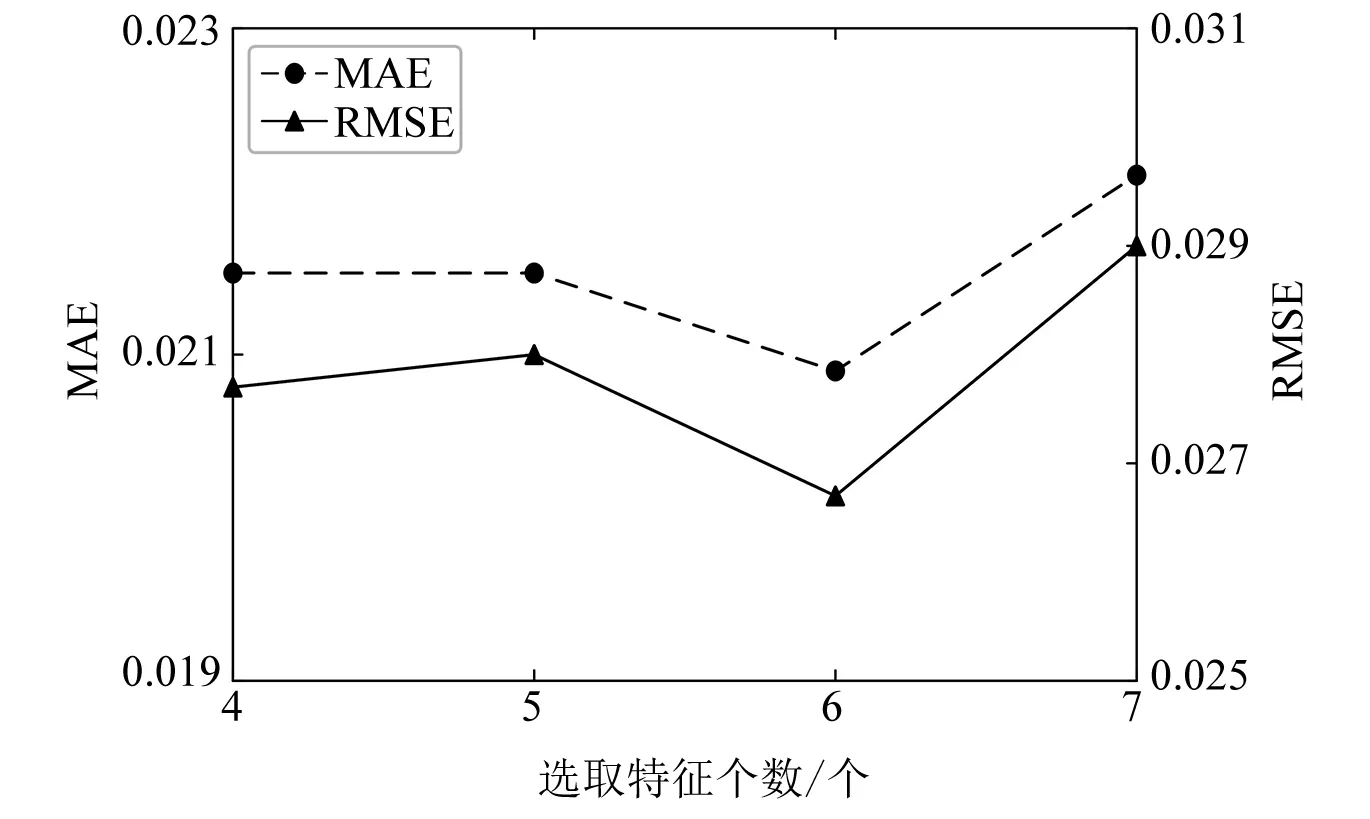
图5 不同特征数的预测结果
从图5可以看出,选择重要性得分前6位的特征形成特征向量,并作为预测网络的输入,此时的序列信息表达最为丰富,负荷预测精度最高。
为了进一步提升负荷预测精度,对Bi-LSTM网络的迭代次数和时间步长进行选定,预测结果如表2所示。
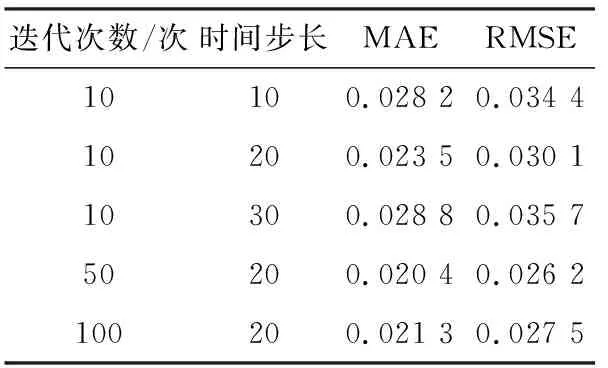
表2 不同参数下预测结果
从表2可以看出,时间步长为20时,预测精度最高,继续增加步长,网络出现梯度消失现象,预测误差增大;当迭代次数为50时,网络拟合度最优,增加或减少迭代次数会导致模型过拟合、欠拟合。因此,神经网络时间步长设为20,迭代次数设为50。
将所提模型(RF-BiLSTM)与LSTM、Bi-LSTM网络模型进行对比,测试集预测误差结果对比如表3所示。
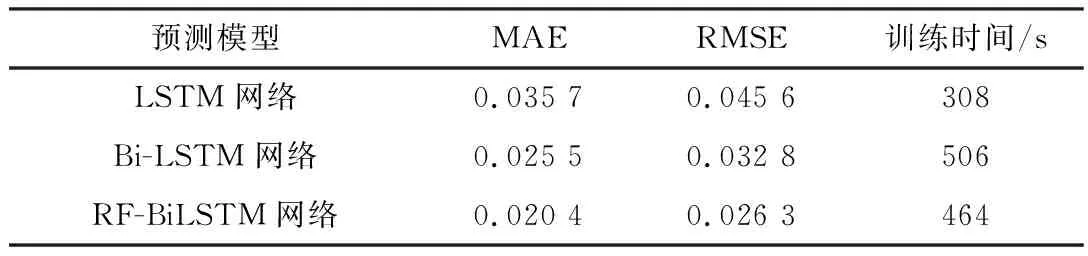
表3 测试集预测误差
LSTM网络处理多维长时间序列时,容易出现梯度消失等问题,预测误差高于其余两个模型。Bi-LSTM网络由两个LSTM拼接而成,能较好地处理长时间序列。预测误差与LSTM网络相比,MAE与RMSE分别下降了0.010 2、0.012 8。RF-BiLSTM网络采用基于随机森林的特征选择算法,选择与负荷关联性强的特征量,降低输入量的维度,提高模型训练效率且预测精度有所提升。与Bi-LSTM相比,MAE与RMSE分别下降了20%、18%,训练时间缩短42 s。
图6、图7分别给出了单周、单日的预测对比图,RF-BiLSTM网络预测曲线与实际负荷拟合程度最高,预测精度最高。
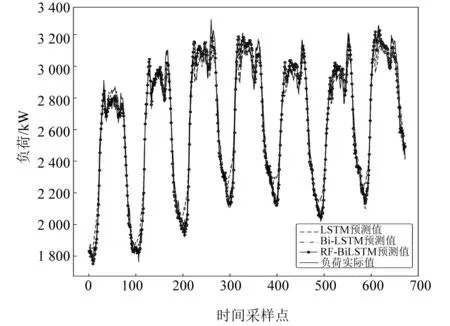
图6 单周预测结果对比图

图7 单日预测结果对比图
5 结束语
为了提高多特征负荷的预测精度,本文提出一种基于随机森林和Bi-LSTM网络的短期负荷预测方法。采用基于随机森林的特征选择算法,选择与负荷关联性强的特征,减少无关特征对模型的影响,提高预测精度以及模型的训练效率。利用某市真实电力负荷数据进行仿真分析,将RF-BiLSTM网络与LSTM、Bi-LSTM网络进行对比,结果表明,基于随机森林和Bi-LSTM网络的融合模型具有较高的负荷预测精度。
