新型高频纵振减摩气缸的滑模运动轨迹跟踪控制

钱鹏飞,浦晨玮,刘磊,吕盘松,何迪,张兵

(1.江苏大学机械工程学院,212013,江苏镇江;2.浙江大学流体动力与机电系统国家重点实验室,310027,杭州)

随着微电子技术和控制理论的发展,伺服控制技术应运而生,气动技术呈现蓬勃发展的新局面[1-5],在核工业、航空宇航等尖端技术领域也占据着重要的地位。然而,气动系统始终没有甩掉运动不平稳、控制精度不高的标签。究其原因,除了气体本身固有的可压缩性、系统的低刚度和低阻尼特性等因素之外,还有系统中不确定强非线性的摩擦特性。为此,实现高精度的气动运动伺服控制,是当前气动技术领域的一个重要研究方向。

目前,提高气缸运动轨迹跟踪控制精度的研究主要集中在气缸摩擦特性的测试、建模及补偿和应用先进的控制策略等方面。摩擦力由于受材料、温度、压力、润滑条件、密封形式、运动状态以及时变特性等诸多因素影响具有不确定性,无法实施准确建模,故在气动运动伺服控制中,基于模型的摩擦力补偿难以精确实施,严重影响系统的控制性能。另外,为了便于控制器的设计,气动运动伺服控制中较少采用复杂的动态摩擦模型,而广泛采用静态摩擦力模型,如常见的静摩擦+库伦摩擦+黏性摩擦模型和Stribeck模型。这样,阀控缸强非线性气动系统中就存在严重的未建模动态和建模误差,需要借助具有强鲁棒性的先进控制策略去抑制。

国内外学者在气缸运动控制策略研究方面做了大量的工作。钱鹏飞详细地阐述了阀控气缸伺服运动系统的基本特性、建模和控制策略的国内外研究现状[6],并针对变负载作用下阀控缸气动系统提出了运动和刚度最大化同时控制的复合滑模控制策略,其在跟踪参考轨迹x=17.5sin(0.5πt)+17.5时,稳态峰值误差为0.3 mm(幅值的1.7%)[7]。Meng等针对比例阀控缸位置伺服系统,提出了一种直接/间接集成的自适应鲁棒控制器,在载荷质量为1.88 kg下,跟踪幅值为125 mm、频率为0.5 Hz的正弦轨迹时,瞬态过程最大跟踪误差为2.27 mm(幅值的1.8%),最大稳态跟踪误差为1.96 mm(幅值的1.57%)[8];此后,孟德远等使用高速开关阀代替比例阀控制气缸,采用对外干扰具有较强性能鲁棒性的自适应鲁棒位置控制算法,该算法在跟踪幅值为90 mm、频率为0.5 Hz的正弦轨迹时的最大绝对跟踪误差为1.51 mm(幅值的1.68%)[9];Lee等为克服气动系统的时变非线性动态和外部扰动,设计了一种自适应傅里叶神经网络滑模控制器(AFNN-SMC+H∞),该控制器在跟踪0.5 Hz的正弦信号时最大稳态跟踪误差为幅值的3.8%[10];周超超等采用自适应鲁棒控制策略设计了基于DSP的嵌入式气动伺服控制器,该气动伺服DSP控制器在跟踪幅值为90 mm、频率小于0.5 Hz的正弦信号时,控制精度能达到5%以内[11];Meng等开发了嵌入式可编程气动伺服DSP控制器,并将自适应鲁棒控制策略中融入到该控制器中,在跟踪x=125sin(πt)正弦信号时,最大跟踪误差为1.2 mm(幅值的0.96%)[12];Zhao等设计了基于线性扩展状态观测器的主动扰动抑制控制器以处理执行器饱和的阀控无杆缸气动系统的精确定位控制问题,实验结果显示该控制器可显著的改善该气动系统的定位精度(实验室研究阶段的稳态定位误差小于0.005 mm),不过其正弦运动轨迹跟踪精度一般(最大稳态跟踪误差为幅值的5%以上)[13]。综上所述,发现在现有的硬件基础上实现气缸运动轨迹跟踪控制的精度已趋于瓶颈。

机械振动通常会带来困扰,在某些方面抑制振动是非常迫切的[14]。然而,近年来对于超声减摩技术在加工、驱动和机械减摩等领域的成功应用,利用振动也逐渐引起了气动领域相关学者的兴趣。部分研究人员近年已经开展了一些研究,将高频振动作用于气缸摩擦副的表面实现了气缸减摩。Liu等把压电执行器安装在气缸活塞杆端部和滑台之间,利用高频颤振来补偿气动定位装置的非线性运动特性,采用PID控制器实现了0.1 μm的定位精度[15]。Cheng等为改善橡胶和金属间的静摩擦特性,先后搭建了超声振动下的氯丁橡胶-铝合金和丁腈橡胶-铝合金的平面摩擦副摩擦特性实验台,研究表明金属和橡胶间的超声减摩现象是存在的[16-17];通过在双联气缸的外缸壁安装超声振荡器以探究振动频率、激振电压、相对振动位置等对静摩擦特性的影响,得出谐振频率周围的减摩效果最为突出以及在一定范围内增加激振电压可增强减摩效果的主要结论[18-19]。肖承丰研发了基于超声换能器的缸筒纵向振动模态的超声减摩气缸和基于贴片式的缸筒弯曲振动模态的超声减摩气缸,实验表明超声振动下气缸摩擦力的稳定性增加、重复性增强[20]。Pham等为探究密封件对超声换能器的阻尼影响,设计将超声换能器添置到气缸活塞处以使其轴向高频振动,通过建立换能器与密封件接触下的等效电路模型,辨识了密封件的阻尼系数和耦合系数[21]。Gao等设计了一种将压电叠堆集成在气缸筒外壁的气缸结构样机,后又开发了一种基于压电叠堆逆压电效应的且可实现弯曲和纵向两种振动模态的减摩气缸,通过对振幅、气压和振-滑速比等因素的研究发现,弯振模态具有更好的减摩效果,气压增大会削弱减摩效果,纵向振动模态中减摩效果只出现在振速与滑动速度之比大于1的情况下[22-23]。上述研究主要侧重于探讨实现气缸的减摩,而对于减摩后气缸的轨迹跟踪性能缺乏细致研究。

因此,本文基于压电叠堆的逆压电效应设计了一款新型高频纵振减摩气缸,并构建基于模型的非线性积分滑模控制器来研究高频振动减摩后气缸的运动轨迹跟踪性能。

1 纵振减摩气缸设计

为了提高气缸的运动轨迹跟踪精度,根据振动减摩原理提出了如图1所示的高频纵振减摩气缸,通过改善气缸的摩擦特性实现。该高频纵振减摩气缸是通过对现有气缸的活塞-活塞杆组件重新设计实现的。新的活塞-活塞杆组件包括1个细长活塞、1个套筒、2个柔性铰链、2个压电叠堆、1个预紧螺母、1个动密封圈和1个静密封圈。套筒底部开设两个中心对称的凹槽,用于放置柔性铰链和压电叠堆,细长活塞穿过套筒,使得活塞端面压住压电叠堆,并用预紧螺母进行预紧。其中柔性铰链用于承受压电叠堆产生的微小位移,提高压电叠堆的使用寿命。图1(b)中套筒底部还设有两个中心对称的凸台,相应的在活塞端面设有两个凹槽,通过凸台与凹槽的配合,防止预紧时产生扭转应力,造成压电叠堆的损坏。本文设计的活塞密封槽选用V型结构,具体尺寸如下:两侧壁夹角为60°,槽宽为3.6 mm,槽深为1.88 mm。

(a)纵振减摩气缸结构

图2 纵振减摩气缸的工作原理 Fig.2 Working principle of longitudinal vibration friction-reducing pneumatic cylinder

本文最终研制出的纵振减摩气缸样机及其工作原理如图2所示。压电叠堆的导线穿过细长活塞与套筒之间的间隙,并从套筒顶部的开口引出。考虑到易于实现和适于减摩的目的,该纵振减摩气缸采用一阶纵向振动模态。工作原理如下:信号发生器产生一定频率的正弦偏置信号,该信号经功率放大器放大调节至合适的电压信号后同时输出给两个压电叠堆以实现同步驱动,压电叠堆产生与活塞-活塞杆组件轴向平行的振动,使得活塞-活塞杆组件处于高频纵向振动状态,此时套筒与前端盖之间的摩擦副、活塞与缸筒内壁之间的摩擦副均发生高频纵振,从而达到了减小摩擦的目的。其中,该原装气缸是费斯托公司的DSBC-32-150-PPVA-N3型号气缸,细长活塞、套筒和柔性铰链均采用430F不锈钢材料加工而成,压电叠堆来自芯明天公司,型号为MTP150/5×5/10,信号发生器来自普源精电科技公司,型号为DG1022U,功率放大器来自隆仪电子科技公司,型号为LYAP-250A。

当高频纵振减摩气缸发生共振时,振幅达到最大,此时减摩效果也达到最佳。因此,需要确定该纵振减摩气缸样机的谐振频率以进行后续实验研究。本文采用致新精密电子有限公司型号为ZX70A的阻抗分析仪对气缸样机进行了阻抗测试,得到其一阶纵向振动的谐振频率为5 860 Hz。

2 气动位置伺服系统建模

为了开展纵振减摩气缸的运动轨迹跟踪控制研究,搭建了一个基于比例方向阀控缸的气动位置伺服控制系统模型,如图3所示,系统模型主要由气缸模型和比例方向阀模型两部分组成。

图3 比例方向阀控缸系统模型 Fig.3 Proportional directional valve-controlled cylinder system model

2.1 气缸模型

根据牛顿第二运动定律,气缸活塞的运动方程可以描述为

(1)

式中:M为运动部分的有效质量;x为活塞的位移;pa、pb分别为无杆腔、有杆腔的气压;Aa、Ab分别为无杆腔、有杆腔中活塞的受力面积;Ff为气缸摩擦力;Fl为外负载力。

由于气缸摩擦力的不确定性,致使其模型难以被准确建立。因此,本文利用搭建的气缸摩擦力测试台[24],将纵振减摩气缸的两个腔室均连通大气,在不施加激励电压和对压电叠堆施加频率为5 860 Hz、振幅为45 V和偏置为45 V的正弦电压信号时,分别测得多个恒定速度下的摩擦力,拟合得到两条摩擦特性曲线。测试结果如图4所示,可知高频共振能够减小气缸摩擦。

为了便于后续运动轨迹跟踪控制研究中基于模型的控制器的设计,采用如下平滑的简化摩擦模型[25]替代,即

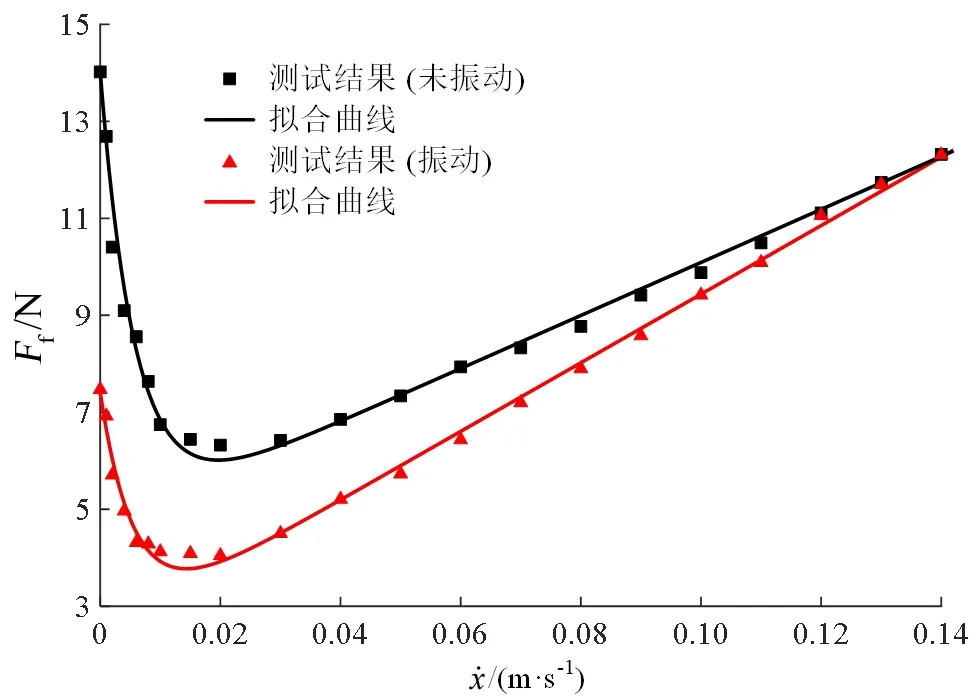
图4 纵振减摩气缸摩擦测试结果 Fig.4 Friction test results of longitudinal vibration friction-reducing pneumatic cylinder

(2)

式中:bv为黏性摩擦力系数;Af为库仑摩擦力的幅值。

假设气缸两腔气体的与外部大气无热交换,充放气时腔内温度不变,且等于环境温度。那么气缸热力学方程可以描述为

(3)

假设气缸行程的中间位置为活塞位移零点,活塞向右移动为位移正方向,向左移动为位移负方向,那么气缸两腔容积为

(4)

式中:Vad、Vbd分别为无杆腔、有杆腔的死区容积;L为活塞行程。

2.2 比例方向阀模型

本文选择费斯托公司型号为MPYE-5-1/8-HF-010B的比例方向阀作为控制阀,下面采用国际标准ISO6358中的流量公式用于描述该控制阀阀口的流量特性

(5)

(6)

式中:A(u)为有效阀口面积,u为阀的控制电压;Cd为修正项;C1为常数;pu、pd分别为阀口上游、下游气压;Tu为阀口上游气体的温度;β为临界压力比。

由于该比例方向控制阀的频响比该气动系统的频响大的多,因此忽略阀芯的动态。通过对若干比例方向阀测试后,发现控制电压与阀芯位移间的线性度很好。此外,测试中也发现该型号比例方向阀是对称但非匹配的,通过对该比例方向阀进行相关流量测试,得到如图5所示的阀口面积与控制电压之间的关系,需要注意的是该阀存在相当明显的死区,且中位电压并不正好是5 V。

图5 比例方向阀有效阀口面积与控制电压的关系Fig.5 Relationship between effective valve port area and control voltage of proportional directional valve

2.3 系统动态模型

通过组合以上气缸和比例方向阀的数学模型,从比例方向阀控制电压的输入到活塞位移的输出,整个气动系统动态可以描述为

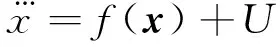
(7)

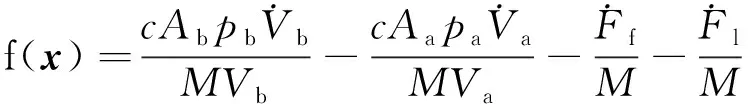
(8)

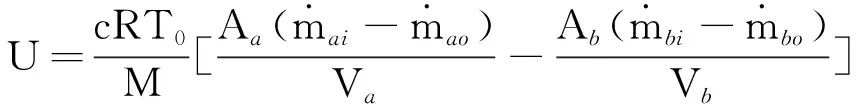
(9)

式中状态矢量x包括活塞的位移、速度和加速度以及气缸两个腔室的压力。

3 控制器设计

本文的主要目的是验证高频振动是否能够提高气动伺服系统运动轨迹跟踪精度,实验中选取不基于模型的传统PID控制器和基于模型的滑模控制器分别进行验证。为了保证比例方向阀控缸系统在跟踪参考运动轨迹时的跟踪精度,选择有利于提高控制系统稳态性能的积分滑模面

(10)

式中:λ为控制增益;e=x-xr为运动轨迹跟踪误差。

于是可以推导出等效控制项

(11)

通过在等效控制项中加入一个鲁棒控制项,可以得到鲁棒控制律

(12)

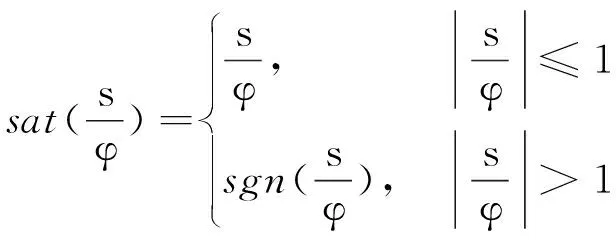
(13)

式中:η为一个正常数;α为系统模型的不确定度;φ>0为边界层厚度。

结合式(5)、(9)和(12),并根据图5所示的比例方向阀有效阀口面积与控制电压之间的关系曲线，可以获得比例方向控制阀的输入信号u。

4 实验研究

为了验证高频振动能够提高气缸的运动轨迹跟踪精度,搭建了如图6所示的比例方向阀控制振动减摩气缸系统的实验台。图7为基于比例方向阀控制纵振减摩气缸的气动位置伺服系统原理图。纵振减摩气缸两个腔室通过型号为MPYE-5-1/8-HF-010B的比例方向阀控制进气和排气,使用一个HERMITT公司型号为KTC-350的直线位移传感器获取气缸活塞的位移x,使用3个瑞士富巴公司型号为511.931003741的压力传感器分别获取供气压力ps、气缸无杆腔压力pa、有杆腔压力pb。获取的位移信号和压力信号通过研华科技公司型号为PCI-1716的数据采集卡的AI端口传输至计算机,执行控制算法后,通过AO端口输出模拟信号,驱动比例方向阀控制纵振减摩气缸样机的运动。

图6 纵振减摩气缸运动轨迹跟踪实验台 Fig.6 Motion trajectory tracking test bench of longitudinal vibration friction-reducing pneumatic cylinder

图7 气动位置伺服系统原理图Fig.7 Schematic diagram of pneumatic position servo system

结合Simulink/xPC建立了比例方向阀控制纵振减摩气缸的实时控制平台,控制频率设置为1 000 Hz。整个实验过程中始终保证气缸样机的谐振频率为5 860 Hz,控制电压幅值为45 V,偏置为45 V。

首先,对幅值为30 mm、频率为0.25 Hz的正弦参考信号采用不基于模型的PID控制器控制高频纵振气缸样机进行运动轨迹跟踪实验,如图8所示,当气缸运动至8 s时,压电叠堆被激发,气缸样机产生高频纵振,PID控制器参数选择Kp=180、Ki=350、Kd=1.8。根据图8所示的实验结果,施加振动前,即0～8 s,正弦参考轨迹的最大跟踪误差为1.69 mm,均方根误差为0.406 mm,施加振动后,即8～16 s,正弦参考轨迹的最大跟踪误差为1.34 mm,均方根误差为0.34 mm。通过比较施加振动前后的运动轨迹跟踪误差结果可以看出,与无振动时相比,高频振动后气缸的最大跟踪误差和均方根误差分别降低了20.71%、16.26%,初步得到了本文所设计的高频纵振减摩气缸可以实现更高的运动轨迹跟踪精度。

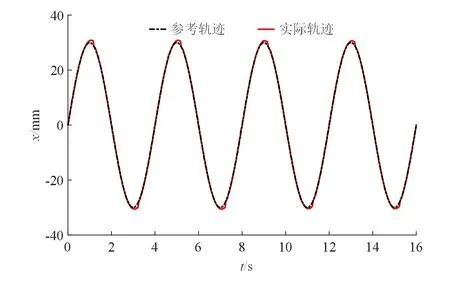
(a)跟踪曲线

对幅值为30 mm、频率分别为0.25、0.125 Hz的正弦参考信号采用基于模型的滑模控制器控制高频纵振气缸样机进行运动轨迹跟踪实验(摩擦力模型参数是由不振动时测得的曲线得到的),压电叠堆均在气缸运动过程中突然被激发,使得气缸样机产生高频纵振,实验结果如图9、10所示。用到的系统模型参数如下:M=0.32 kg,ps=0.5 MPa,Aa=8.04×10-4m2,Ab=6.91×10-4m2,Fl=0 N,bv=50.84 N·s/m,Af=4.981 N,c=1.4,R=287 N·m/(kg·K),T0=300 K,Vad=1.1×10-5m3,Vbd=0.6×10-5m3,L=0.06 m,C1=0.040 4,β=0.29。滑模控制器参数选择如下:λ=100,η=1 500,α=0.1,φ=10。从图9中可以看出,跟踪0.25 Hz参考轨迹时,施加振动前,即0～9 s的最大跟踪误差为1.02 mm,均方根误差为0.418 mm,而施加振动后,即9～18 s的最大跟踪误差为0.82 mm,均方根误差为0.359 mm。与无振动时相比,高频振动后气缸的最大跟踪误差和均方根误差分别降低了19.61%、14.11%。从图10中可以看出,跟踪0.125 Hz参考轨迹时,施加振动前,即0～18 s的最大跟踪误差为0.73 mm,均方根误差为0.265 mm,而施加振动后,即18～36 s的最大跟踪误差为0.58 mm,均方根误差为0.218 mm。与无振动时相比,高频振动后气缸的最大跟踪误差和均方根误差分别降低了23.29%、17.74%,进一步验证了高频纵振能够提高气缸的运动轨迹跟踪精度。

(a)跟踪曲线

(a)跟踪曲线

综上两次实验结果,无论是采用不基于模型的传统PID控制器还是基于模型的具有更强鲁棒性的滑模控制器,该高频纵振减摩气缸进行运动轨迹跟踪控制时,其运动控制精度均可被提高,即验证了本文采用的通过高频共振的方法改善气缸的运动控制性能是可行的。

5 结 论

本文基于逆压电效应和振动减摩原理,设计了一种新型的高频纵振减摩气缸,通过阻抗测试,得到其谐振频率。采用不基于模型的PID控制算法和基于模型的积分滑模控制算法,分别对纵振减摩气缸进行了运动轨迹跟踪实验,实验表明高频振动可以一定程度上改善气缸的运动控制精度。当纵振减摩气缸的高频共振模式被激发后,气缸的运动轨迹跟踪精度得到了大约20%的提高。今后将尝试其他先进的控制算法,以实现气动系统更高精度的运动轨迹跟踪控制,同时进一步论证高频共振提高气缸的运动轨迹跟踪精度与使用的控制算法无关。