合理分类有序转化
2022-11-02何平
文/何平
“对称图形——圆”这一章涉及的数学思想方法很多,老师将和大家一起来学习圆中的分类思想和转化思想。
我们在解决圆中有关计算问题时,通过对条件进行分析,发现条件和结论不确定时,往往需要分类讨论。通过寻找分类的对象和明确分类的标准,我们可以做到不重复、不遗漏地得出答案,从而全面地思考问题,让思维更加缜密。
例1在⊙O中,弦AB所对圆心角为70°,则弦AB所对的圆周角为___。
【分析】因为题目中弦AB所对的圆周角位置不确定,所以需要分类。分类的对象是圆周角,分类的情况是圆周角的顶点在弦AB所对的两条弧上。
解:如图1,当点P1在︵上时,

图1
∵∠AOB=70°,∴∠AP1B=35°。
当点P2在上时,
∵∠AOB=70°,

因此,弦AB所对的圆周角是35°或145°。
例2已知⊙O直径CD与弦AB垂直,垂足为H,若AB=6,CD=10,则AC=___。
【分析】因为题目中弦AB的位置不确定,所以需要分类。分类的对象是弦AB,分类的情况是弦AB在圆心的两侧。
解:如图2,连接OA。

图2

如图3,CH=CO-OH=1,
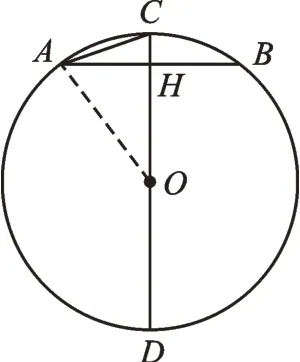
图3
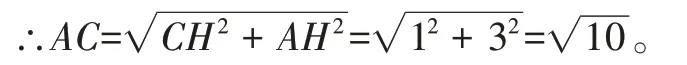
因此,AC=3或。
【点评】通过这两道例题,我们可以发现,分类思想蕴含在最基本的点、直线、角与圆的位置关系等图形中,常见的有圆周角的分类、弦的位置分类等。总之,当问题中条件或结论中的相关量不确定时,就要明确分类方法,合理进行分类讨论。
转化思想在圆这一章中同样被广泛地运用在计算与证明中。对于圆中的相关问题,通过对条件与结论的分析,借助最近联想,适当添加辅助线,可以将圆中较为复杂的图形逐步分解成同学们熟悉的基本图形,从而实现对复杂问题的转化。
在同圆或等圆中,由弦相等得弧相等
例3如图4,在⊙O中,弦AB、CD相交于点P,若AB=CD。求证PB=PD。

图4
【分析】要证明两边相等,通常可以借助三角形全等或者“等角对等边”等方法来解决。观察图形,容易联想到连接BD,再证明∠B=∠D即可。
证明:如图5,连接BD。

图5

【点评】本题从结论出发,寻找结论与条件之间的联系,将条件中的相等的弦转化为对应的弧相等,从而得到对应的圆周角相等。解决问题时,我们只有树立将同圆或等圆中的圆心角、弧、弦三者之间的关系进行有序转化的意识,才可以优化解题过程。
圆中内接多边形的转化
例4如图6,在⊙O的内接六边形ABCDEF中,∠A+∠C=220°,则∠E=°。
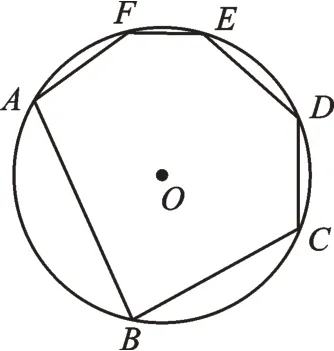
图6
【分析】本题是圆内接六边形的角度计算,只要添加辅助线BE即可将圆内接六边形转化为圆的两个内接四边形。
解:如图7,连接BE。
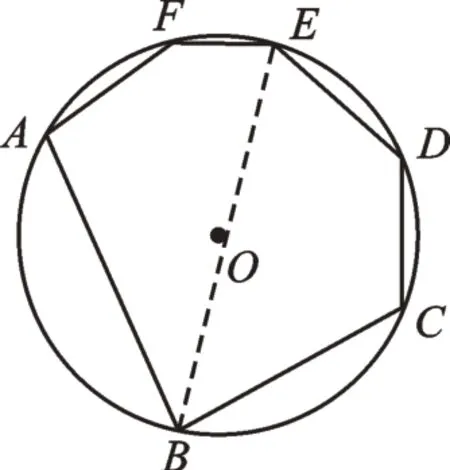
图7
∵四边形ABEF是⊙O的内接四边形,
∴∠A+∠BEF=180°。
同理,∠C+∠BED=180°。
∴∠A+∠BEF+∠C+∠BED=360°。
又∵∠A+∠C=220°,
∴∠BEF+∠BED=360°-220°=140°。
∴∠E=140°。
【点评】对于圆内接多边形中角度的计算问题,我们需要添加适当的辅助线将复杂的图形转化为圆的内接四边形或者三角形。因此,转化是解决此类问题的关键。
圆中阴影部分面积的转化
例5如图8,圆形时钟的半径为2,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为____。

图8
【分析】通过连接半径,可以将阴影部分面积转化为扇形AOB的面积与△AOB的面积之差。
解:连接OA、OB,过点O作OC⊥AB于点C,由题意可知∠AOB=60°。

图9
∵OA=OB,∴△AOB为等边三角形。
∴AB=AO=BO=2。
∵AO=BO,OC⊥AB,
∴∠OCA=90°,AC=1。∴OC=。

又∵
∴阴影部分的面积为
【点评】对于阴影部分面积的计算,我们通常将不规则的图形进行分解,转化为与之相关联的规则图形后再进行计算。正确添加辅助线,可以将图形进行有效的转化。
