基于深度强化学习的固定翼飞行器六自由度飞行智能控制

章 胜 杜 昕 肖 娟 黄江涛

1.中国空气动力研究与发展中心 四川绵阳 621000 2.空气动力学国家重点实验室 四川绵阳 621000

无人机在军事上具有显著的优势.从20世纪70年代末以色列研制第一款现代意义的无人机先驱者开始,无人机已成功应用于海湾战争、阿富汗战争与高加索纳卡冲突等战争,在作战行动中发挥了重要的作用.美国一位著名的军事评论家就曾指出“到目前为止,没有比无人战斗机更富有意义的未来军事技术了”.可以预见,在未来战争中,无人机将会发挥越来越大的作用.

无人机飞行控制是无人机系统的关键技术,发展无人机先进自主控制能力是各军事强国不断追求的目标.飞行器是典型的非线性系统,目前包含无人机在内的航空飞行器飞行控制通常采用线性增益调度控制器,其中,涉及到若干工作状态点的选取与相应线性控制器的设计,参数整定工作繁琐[1].除线性控制器外,现代控制技术,包括动态逆控制[2]、反步控制[3]、滑模控制[4]等,在飞行器飞行控制的应用中也得到了大量研究.总的说来,这些控制方法很好地实现了控制目的,取得了良好的控制效果.但是经典控制和现代控制理论的主要特征是基于模型的控制,而实际中对系统尤其对复杂系统的建模总是存在一定误差,虽然基于模型的控制方法可以解决一定程度的不确定性,但是对于飞行器这种涉及到力、电、机械等环节的复杂对象,可能存在某些认识不足的不确定性因素,这会影响控制效果甚至带来灾难性后果.比如:飞行器在过失速大迎角下的气动特性存在非线性非定常效应,其中的空气流动机理目前尚未完全掌握[5],准确的气动力建模存在诸多困难,飞行器在过失速状态下可能进入危险的“尾旋”状态.此外,传统的飞行控制方法通常将飞行器控制割裂为外环航迹控制与内环姿态控制[6],并对系统的非线性耦合效应进行抑制,这也会在一定程度上影响飞行器的性能.

人工智能的研究可以极大地解放生产力与发展生产力,给人类社会带来历史性的变革.学习是智能的本质特征,强化学习适用于动态决策控制问题,是最接近于生物学习机制的一种学习范式.基于强化学习,智能体可以通过与环境进行交互,学习探索回报极大化的行为策略[7].相对于经典控制和现代控制方法,强化学习提供了能自适应自优化、独立于模型、广泛适用于各种对象的控制器设计框架,是实现智能控制的有效途径.神经网络是模仿人类大脑结构和功能的一种有效的建模工具[8].相对于浅层神经网络,深度神经网络可以学习到更加复杂的特征,具有更好的性能[9].结合深度神经网络的强化学习即深度强化学习（deep reinforcement learning,DRL）,DQN（deep q network）算法是最早提出的有效DRL 方法之一,它在Atari 游戏上达到了人类玩家的水平,但是其只能解决动作离散的问题[10].DDPG（deep deterministic policy gradient）算法是在DQN 基础上进一步发展的针对“连续动作”问题的DRL 方法,有效实现了机器人的运动控制[11],是现今解决“连续状态、连续动作”类型问题的主流算法之一.

不同于现有的飞行控制技术路线,深度强化学习方法可以习得被控对象的个体特性,充分利用航迹与姿态动力学之间的耦合特性,实现端到端的一体化控制,具有发展更优性能控制机的潜力.最近美国国防部高级研究计划局（DARPA）主持的空战演进（air combat evolution,ACE）项目吸引了全球各国的目光,其中,通过深度强化学习得到的人工智能在竞赛中完胜顶尖F-16 人类飞行员.ACE 项目旨在实现无人机近距空战的智能决策,通过针对六自由度模型的学习以提升飞行器的作战效能[12].由于只有在习得稳定飞行能力的前提下,才可能实现六自由度的对抗,因此,智能飞行控制是空战对抗智能决策的基础[13].文献[14]采用DDPG 方法,实现了四旋翼飞行器机动悬停与前进的六自由度智能控制.相较于旋翼飞行器,固定翼飞行器的动力学模型更为复杂,其智能飞行控制机也更难获得.文献[15]基于DQN 算法的一种发展变体,实现了固定翼飞行器两种机动动作的智能控制,有效利用了飞行器的气动性能与非线性质心/绕质心运动耦合特性.文献[16]采用DDPG 算法研究了固定翼飞行器的六自由度飞行控制,实现了给定速度、高度指令下的巡航飞行,但是该智能控制机不具有可拓展性,只能实现标称指令,同时习得的飞行为带侧滑飞行.本文进一步改进了固定翼六自由度飞行智能控制学习算法,开展了采用偏航角误差作为智能控制机输入以消除飞行器侧滑的研究,并尝试发展具有一般通用性的端到端固定翼飞行智能控制机.

1 飞行器运动动力学模型

1.1 运动动力学方程

首先定义飞行器机体坐标系b 与地面坐标系g[17].体系b 与机体固连,原点ob位于飞行器质心,obxb轴在飞行器对称面内并指向机头,obyb轴垂直于飞行器对称面指向机身右方,obzb轴在飞行器对称面内指向机身下方.地面系g 固定于地面,原点og位于地面某点,ogxg轴在水平面内指向某一方向,ogzg轴垂直于水平面并指向地心,ogyg轴通过右手定则确定.

假设飞行器推力沿体系x 方向,飞行器的航迹运动动力学方程为

飞行器的姿态运动动力学方程为

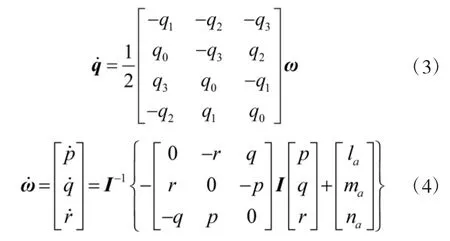
另一方面,基于姿态四元数q,可以求得飞行器的欧拉姿态角为

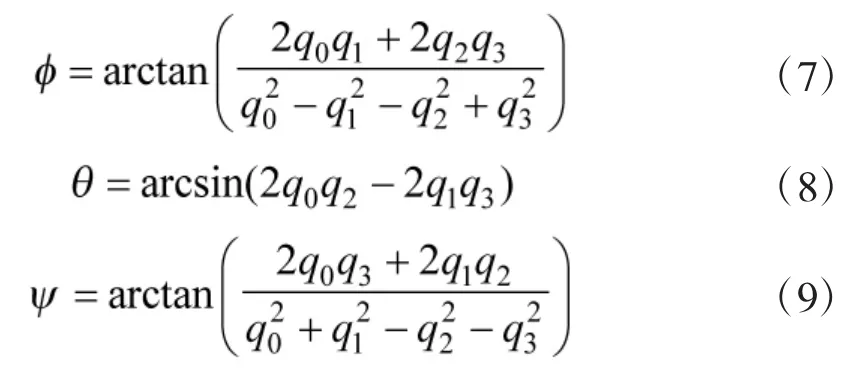
1.2 气动力（矩）模型

飞行器的气动模型形式如下

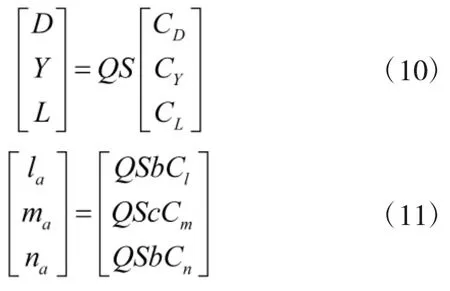
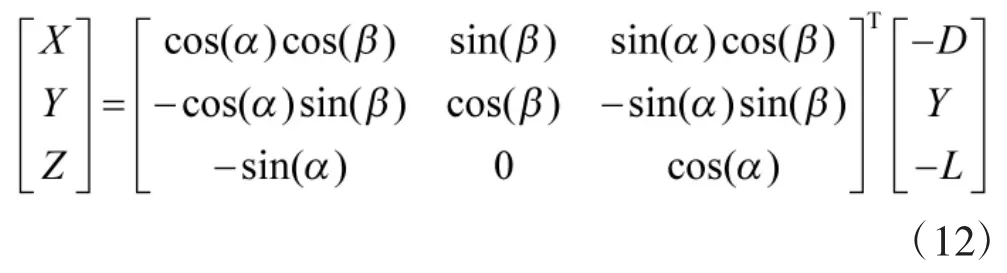
由于动导数对气动力影响很小,故气动力系数中不考虑动导数项.但是动导数引起的气动力矩系数可能与静态气动力矩系数数值大小相差不多,因此,气动力矩系数中需要考虑动导数项,它们的形式分别为

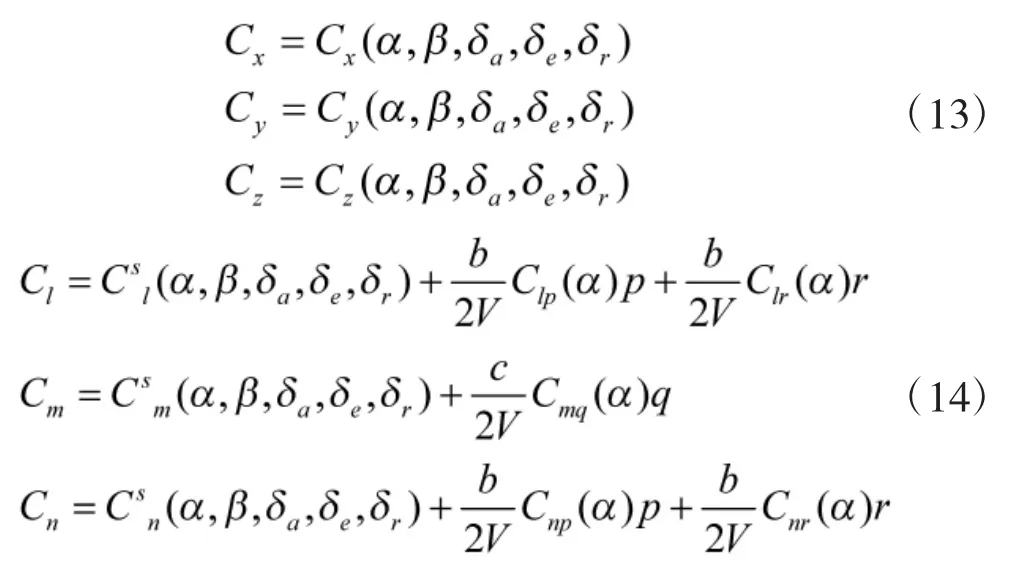
本文研究对象为全尺寸F/A-18 固定翼飞行器,其质量为m=15 119 kg,惯量为Ixx=31 184 kg·m2、Iyy=205125kg·m2、Izz=230414kg·m2、Ixz=-4028.1kg·m2[18],文献[19]详细给出了该飞行器的气动模型.

2 强化学习基本理论与DDPG 方法

2.1 强化学习理论基础

强化学习的核心思想在于智能体与环境的试错交互：在每一时刻t,智能体从当前状态xt出发,执行动作ut,从环境接收奖励信息rt,环境根据其状态转移函数P 得到下一时刻状态xt+1,智能体从新的状态出发再执行新的动作,如此循环实现与环境的交互以获得最优动作策略π.在数学上该过程可以采用马尔科夫决策过程（Markov decision process,MDP）进行描述.

MDP 由状态集合、动作集合、状态转移函数和回报函数组成,其定义可以表示为一个四元组（x,u,r,P）,它满足马尔科夫性：即当前状态向下一状态转移的概率和奖励值仅与当前状态和动作有关,而与历史状态和历史动作无关.在奖励函数r 的基础上,MDP的回报函数可以定义为学习周期（episode）中奖励函数的折扣求和,即

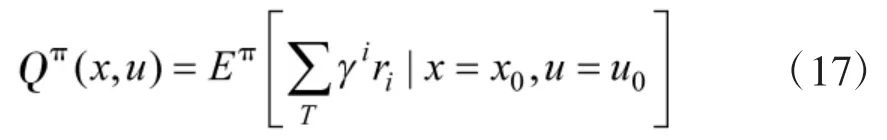
动态规划是求解MDP 的基本原理与方法,行为值函数（及状态值函数）满足Bellman 方程：

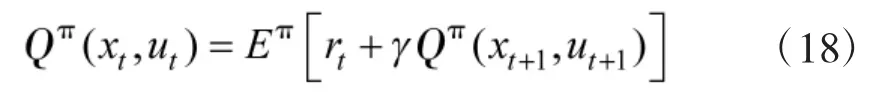
给定一个MDP,强化学习的目标是寻求一个最优策略（确定性或非确定性）使得总回报函数最大,即

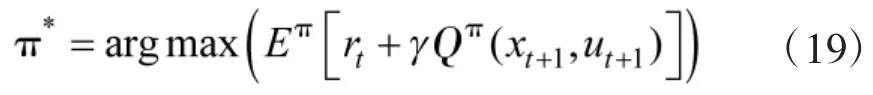
经过多年的发展,强化学习在动态规划的基础上逐步形成了基于值函数的学习方法和直接策略搜索学习方法,并进一步发展了对上述两种方法加以综合的Actor-Critic 架构的学习方法[8,20-21].

2.2 DDPG 方法

DDPG 深度强化学习算法是在DQN 算法基础上为解决“连续动作”类型问题而发展起来的,采用Actor-Critic 架构,其中,Critic 评价在状态x 采用动作u的行为值函数,Critic 网络的参数化表示为表示Critic 深度神经网络的参数,Actor 逼近确定性的动作策略,输出为动作u,Actor 网络的参数化表示为表示Actor 深度神经网络的参数.由于智能体学习的是使Critic 行为值函数最优的策略,DDPG 方法属于off-policy 方法的范畴.Critic 网络参数的更新类似于DQN 中的做法,考虑性能指标

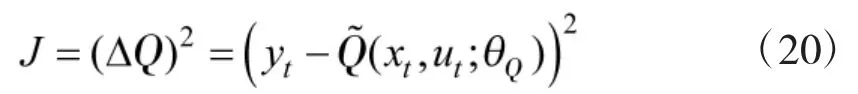
其中,yt表示行为值函数的估计,为行为值函数的预测,表示二者的误差.通过使式（20）减小,可以导出Critic 网络参数的更新律为

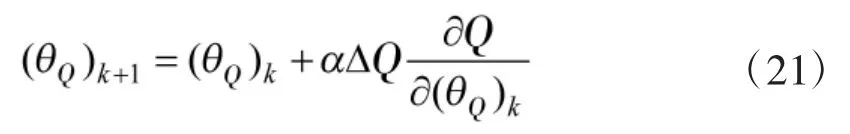
其中,α 为Critic 网络的学习率.另一方面,为了让Actor 网络的输出使得Critic 网络的输出取极大值,根据链式法则,可以推导出行为值函数Q 对Actor 网络参数的梯度为,进而可得到Actor 网络参数的更新律为

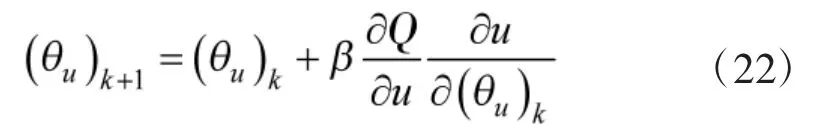
其中,β 为Actor 网络的学习率.

继承DQN 的做法,DDPG 算法还考虑了使参数缓慢更新的目标网络,包括Target-Critic 网络与Target-Actor 网络.目标网络与原始网络结构相同,相应的参数分别为与.通过引入目标网络,使得强化学习类似于监督学习,训练效果更加稳定,有利于提高网络参数收敛性.目标网络参数采用如下更新率

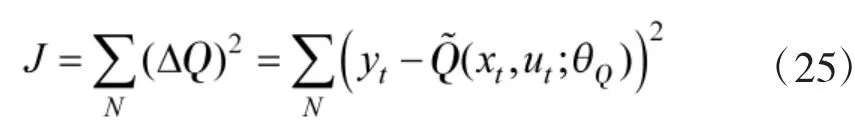
其中,N 为mini-batch 的大小.行为值函数的估计为

相应的,参数更新方程（21）与（22）中梯度需要调整为在mini-batch 数据集上的求和.

3 固定翼飞行智能控制机设计

随着深度学习技术的发展与硬件计算能力的增强,深度神经网络训练效率低、对计算资源消耗大的问题已不再是限制深度（强化）学习研究的瓶颈[23].因此,本文直接利用强化学习中与环境交互得到的奖励函数反馈开展训练,针对固定翼飞行器巡航飞行控制问题发展智能控制机,通过对仿真飞行数据进行学习,使智能控制机能够掌握并运用固定翼飞行器航迹动力学与姿态动力学的耦合效应,实现端到端的一体化优化控制.

开展基于深度强化学习的固定翼飞行器神经网络控制机训练,飞行器巡航中给定的高度指令为hc,速度指令为.在文献[16]中,智能控制机中Actor 网络模型的输入量为高度误差、速度误差、欧拉姿态角与角速度、高度误差积分量、速度误差积分量与,其中,,,积分输入量的引入是参考PID 控制器中积分控制消除稳态误差的做法.由于飞行器稳定飞行时的偏航姿态角与给定的速度指令存在对应关系,即无侧滑时候有

因此,直接采用偏航姿态角作为输入得到的智能控制机不具有向其他巡航控制任务的可拓展性.

为解决这一问题,本文采用偏航姿态角误差作为智能机输入,同样比照PID 控制器中的积分控制,将姿态角误差积分也作为控制机的输入,具体考虑两种输入下的智能机设计.智能控制机I 中Actor 网络模型有13 个状态输入,它们为：高度误差、速度误差、姿态角与角速度、高度误差积分量,速度误差积分量与,其中,.智能控制机II 中的Actor 网络在控制机I 的基础上,进一步引入消除偏航角误差的积分量作为输入.Actor控制机的动作输出有4 个,分别为副翼、升降舵、方向舵与油门.智能控制机I 中Critic 网络模型有17 个输入,智能控制机II 中Critic 网络模型有18 个输入,除与相应Actor 网络相似的状态输入外,还包括4 个动作输入,输出为行为值函数标量值.强化学习中,定义学习周期为若干个控制周期,根据期望的控制目标,采用加权L1 范数定义第k 步的奖励函数,智能控制机I 训练中的奖励函数为

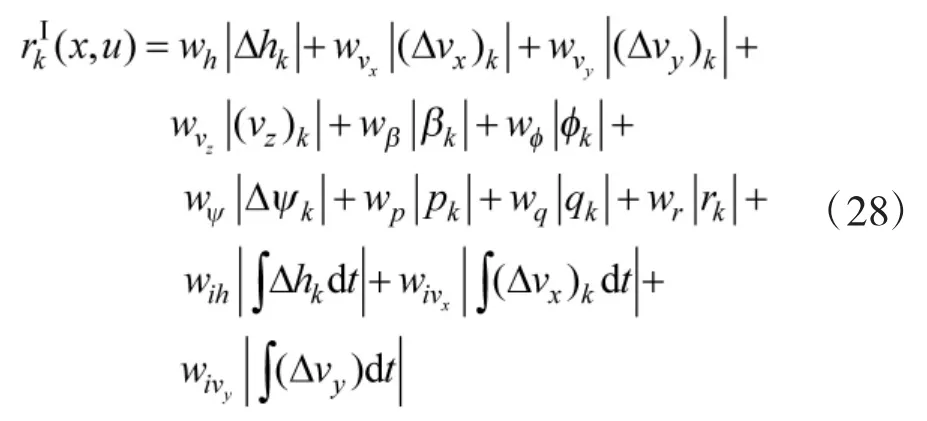
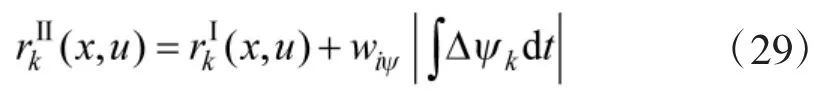
采用“全连接”前馈型多隐层深度神经网络进行飞行器智能控制机建模.智能控制机I 中,Actor 网络为5 层,输入层包含13 个输入单元,输出层有4 个输出单元,网络模型包含3 个隐藏层,隐层单元数分别为32、64 与128,前4 层采用Relu 激活函数,输出层采用Tanh 激活函数.Critic 网络有4 层,除输入层与输出层外,2 个隐藏层的单元数分别为64 与128,前3 层的传递函数为Relu 函数,输出层为线性函数.智能控制机II 中的网络结构与控制机I 比较,除输入层的数目存在区别外,其余相同.

为了保证前向传播和反向传播时每一层的方差一致,训练中采用基于Xavier 方式的均匀分布对Critic 网络与Actor 网络参数进行初始化[24],mini-batch大小取为N=128,训练中一个周期长为5 000ΔT,其中,ΔT=0.1 s,此外若飞行器状态超过一定的门阈值,则训练周期提前结束.奖励函数中的权重系数分别为：.采用Adam 优化方法[24],在一个周期结束后对Critic网络与Actor 网络参数同时进行更新,学习率分别取为与,之后进行目标网络的软更新,更新参数为.深度强化学习中,为平衡探索与利用机制,Actor 网络输出的控制动作将叠加一定幅值的Ornstein-Uhlenbeck 随机噪声[11].

基于Pytorch 开展固定翼飞行器智能控制机的训练,训练中给定的高度指令为hc=100 m,速度指令为vxc=65 m/s,vyc=40 m/s,每个周期中飞行器的初始状态随机生成.相对于四旋翼飞行器的飞行控制,固定翼飞行器的控制要复杂很多,需要同时考虑气动力与气动力矩的平衡,尤其针对全尺寸飞行器,其训练周期相对于小型飞行器更是大为增加.文中训练次数取为60 000 次,图1和图2给出了两种智能机的训练结果,其中,图1给出了终端误差与训练次数的关系曲线；图2给出了单个周期长度与训练次数的关系曲线.从图中可以看到训练中控制机性能并不能单调的改善,然而随着训练次数的增加,终端误差虽呈现跳跃但是总体变小,同时飞行器达到最大飞行周期的次数不断增加,由于智能控制机I 相对于II 的输入更少,从图2中可以看到其在学习中能更快更多地达到最大周期长度.

图1 智能控制机训练中终端误差与训练次数关系曲线Fig.1 Terminal error against number of episodes in the reinforcement learning

图2 智能控制机训练中周期长度与训练次数关系曲线Fig.2 Length of episodes against number of episodes in the reinforcement learning

由于强化学习中不能保证控制机性能的单调改善,可能出现训练次数增加,固定翼飞行器巡航飞行控制效果反而变差,甚至飞行器发生失稳的现象.因此,本文通过在训练中比较一个学习周期结束后的终端误差来选择性能良好的神经网络控制机,并基于此控制机开展飞行仿真.

4 飞行仿真

4.1 标称巡航指令仿真

基于Python 语言平台Spyder 开展固定翼飞行器智能控制的飞行仿真,此处的标称巡航指令指智能控制机训练时采用的指令,即hc=100 m,vxc=65 m/s,vyc=40 m/s,仿真时不再考虑训练中加入的噪声干扰,飞行器从地面坐标系原点位置出发,初始速度为100 m/s,初始方位角为0 deg,仿真时间为1 000 s.表1给出了采用训练得到的智能控制机I 与II 在1 000 s稳定巡航时的状态结果,从表中可以看到,两种控制机均精确地达到了给定的巡航指令,飞行器基本实现了无侧滑的飞行,相较文献[16]中结果（侧滑角为-6.21 deg,滚转角为-5.84 deg）,采用智能控制机I 的飞行中侧滑角与滚转角都很小,而智能控制机II 则实现了零侧滑的飞行.

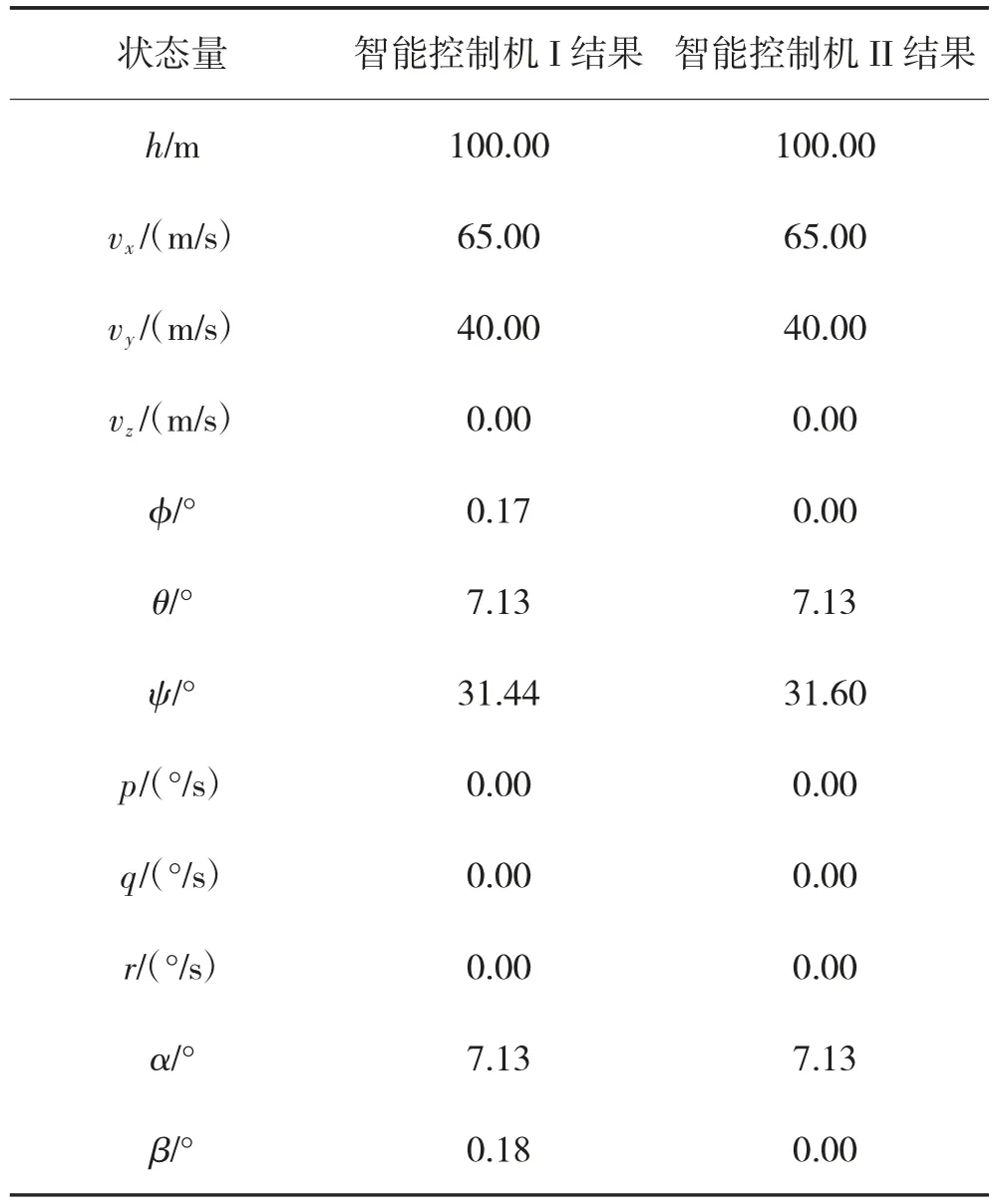
表1 标称指令下飞行器稳定巡航时的状态结果Table 1 The aircraft stable cruise states under standard commands

图3～图9给出了采用智能控制机I 时的飞行状态仿真结果,其中,图3给出了飞行器的地面位置坐标曲线,可以看到飞行器实现了定直飞行.图4给出了飞行器的高度曲线,其中存在一定的超调,但在100 s 后飞行器基本稳定在指令高度,最终相对于指令高度的误差为零.

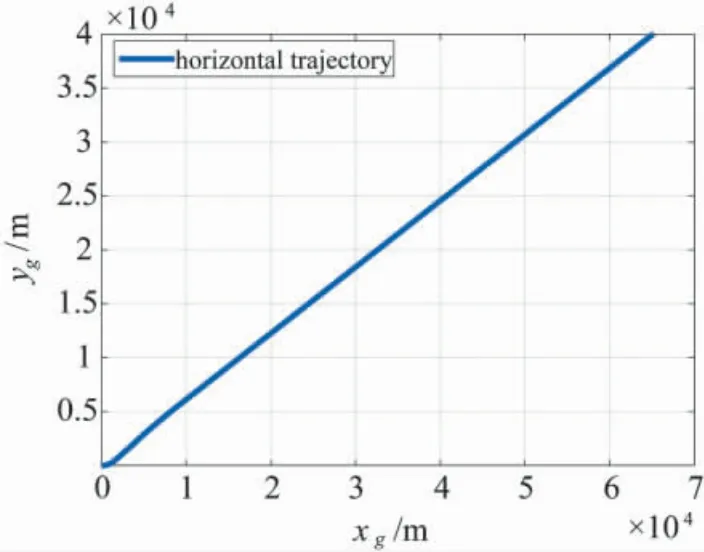
图3 基于智能控制机I 的飞行器水平航迹仿真结果Fig.3 Aircraft horizontal trajectory under intelligent controller I

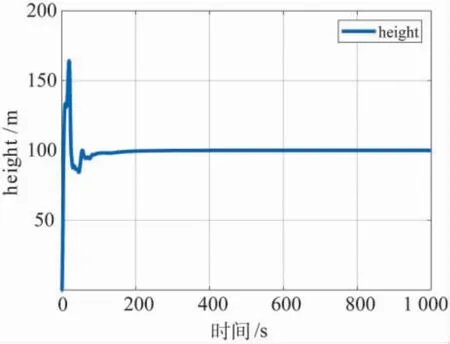
图4 基于智能控制机I 的飞行器高度仿真结果Fig.4 Aircraft height under intelligent controller I

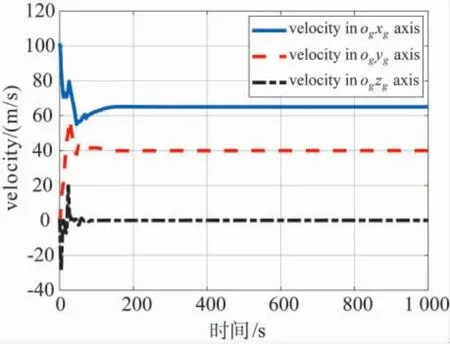
图5 基于智能控制机I 的飞行器速度仿真结果Fig.5 Aircraft velocity under intelligent controller I

图6 基于智能控制机I 的飞行器姿态角仿真结果Fig.6 Aircraft attitude under intelligent controller I

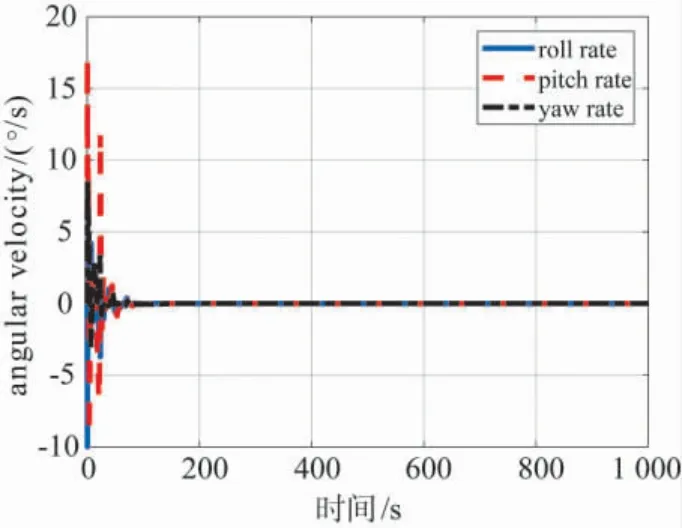
图7 基于智能控制机I 的飞行器角速度仿真结果Fig.7 Aircraft angular velocity under intelligent controller I

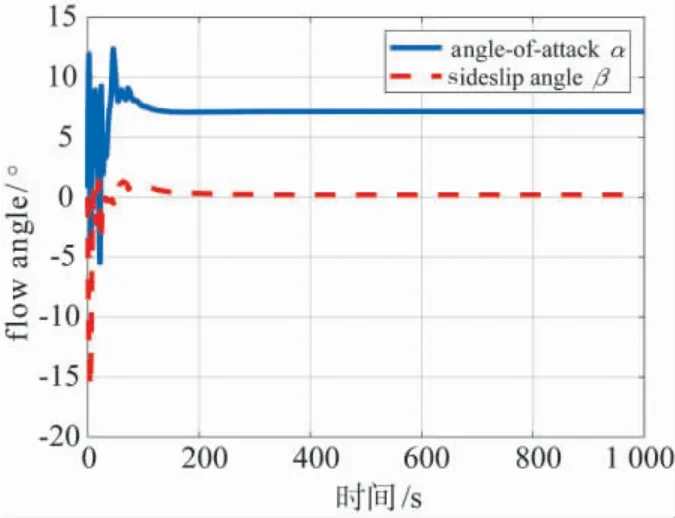
图8 基于智能控制机I 的飞行器迎角、侧滑角仿真结果Fig.8 The angle-of-attack and sideslip angle under intelligent controller I

图9 基于智能控制机I 的飞行器控制仿真结果Fig.9 The aero-surface and throttle control under intelligent controller I

图5给出了飞行器在地面坐标系下的速度曲线,在100 s 后飞行器的速度已基本稳定,它们精确地达到了指令值.图6给出了飞行器的姿态角曲线,其中,偏航角相对于由速度指令导出的指令方位角存在约0.16 deg 的稳态误差.图7给出了飞行器的角速度曲线,它们很快都趋于零值.

图8给出了采用智能控制机I 时飞行器的迎角与侧滑角曲线,从图中可以看到进入稳定飞行后,飞行器的侧滑很小,几乎为零值.图9给出了飞行器的气动舵面与油门控制曲线,除初始阶段变化较剧烈外,大约100 s 后它们都达到了平衡状态.

采用智能控制机II 的飞行仿真结果与采用控制机I 的结果大致相同,但是其实现了完全无侧滑的稳定飞行,图10给出了采用智能控制机II 时的气流角曲线.从图中可以看到,相对于控制机I 下的仿真曲线,它们在过渡过程的超调更为明显,但最终实现了零侧滑与零滚转.分析原因,这是由于引入了偏航角误差积分控制,它在带来对动态品质一定损害的同时,也有效地消除了稳态误差.

图10 基于智能控制机II 的飞行器迎角、侧滑角仿真结果Fig.10 The angle-of-attack and sideslip angle under intelligent controller II

4.2 非标称巡航指令仿真

为进一步考察得到控制机向其他巡航飞行控制任务应用的可扩展性,本节中仿真采用的指令与训练中的指令存在区别,具体考虑下述3 种指令：

指令1：

hc=100 m,vxc=65 m/s,vyc=30 m/s.

指令2：

hc=150 m,vxc=80 m/s,vyc=0 m/s.

指令3：

hc=200 m,vxc=75 m/s,vyc=60 m/s.

飞行仿真的初始条件同第4.1 节,表2给出了3种非标指令情形下,分别采用智能控制机I 与控制机II 达到稳定巡航时的仿真结果,由于对于指令2,智能控制机II 的仿真结果是震荡稳定,对于指令3,智能控制机II 没有实现稳定飞行,故这两种情形的结果未在表中给出.

从针对非标指令的仿真结果中看到,智能控制机I 相对于智能控制机II 具有更好的可拓展性.对该现象进行分析,原因之一可能是智能控制机II 还没有充分训练好,而另一个可能是控制机中采用俯仰角作为输入,由于不同的巡航速度对应的稳态俯仰角不同,这会导致不同巡航飞行时俯仰角的不同取值将影响飞行器的平衡,智能控制机I 中可以通过滚转侧滑来抵消该影响,而智能控制机II 中则不具有这种弹性,从而损坏了控制机对不同任务应用的可拓展性.

图11与图12分别给出了3 种指令情形下基于智能控制机I 的滚转角与侧滑角仿真曲线,结合表2的结果,采用智能控制机I 的飞行虽仍然含有一定的侧滑（及滚转）,但是侧滑角很小,相对于文献[16]采用偏航角作为神经网络控制机输入的仿真结果改进很多,说明了智能控制机I 总体上具有较好的性能.

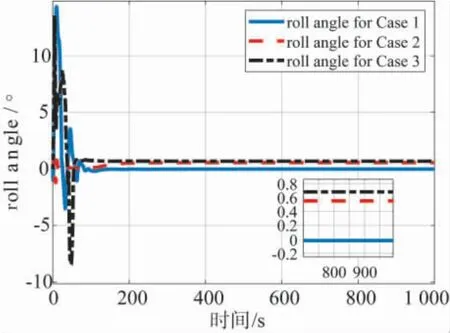
图11 3 种指令情形下基于智能控制机I的飞行器滚转角仿真结果Fig.11 The aircraft roll angle for the three cases under intelligent controller I

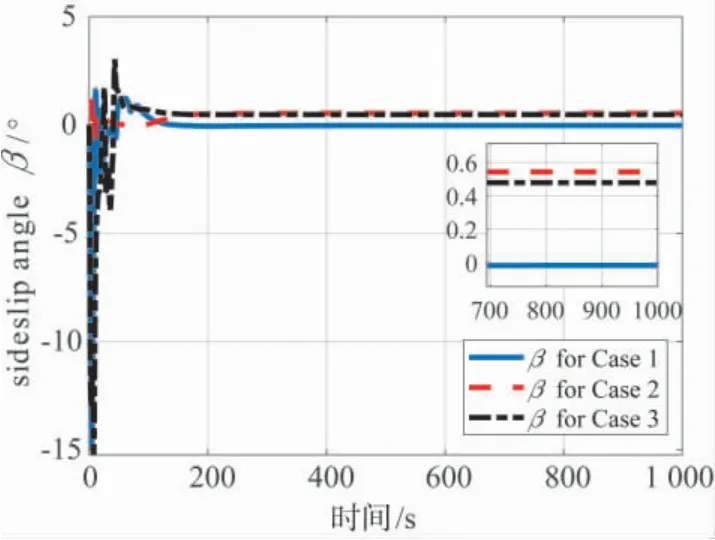
图12 3 种指令情形下基于智能控制机I的飞行器侧滑角仿真结果Fig.12 The aircraft sideslip angle for the three cases under intelligent controller I

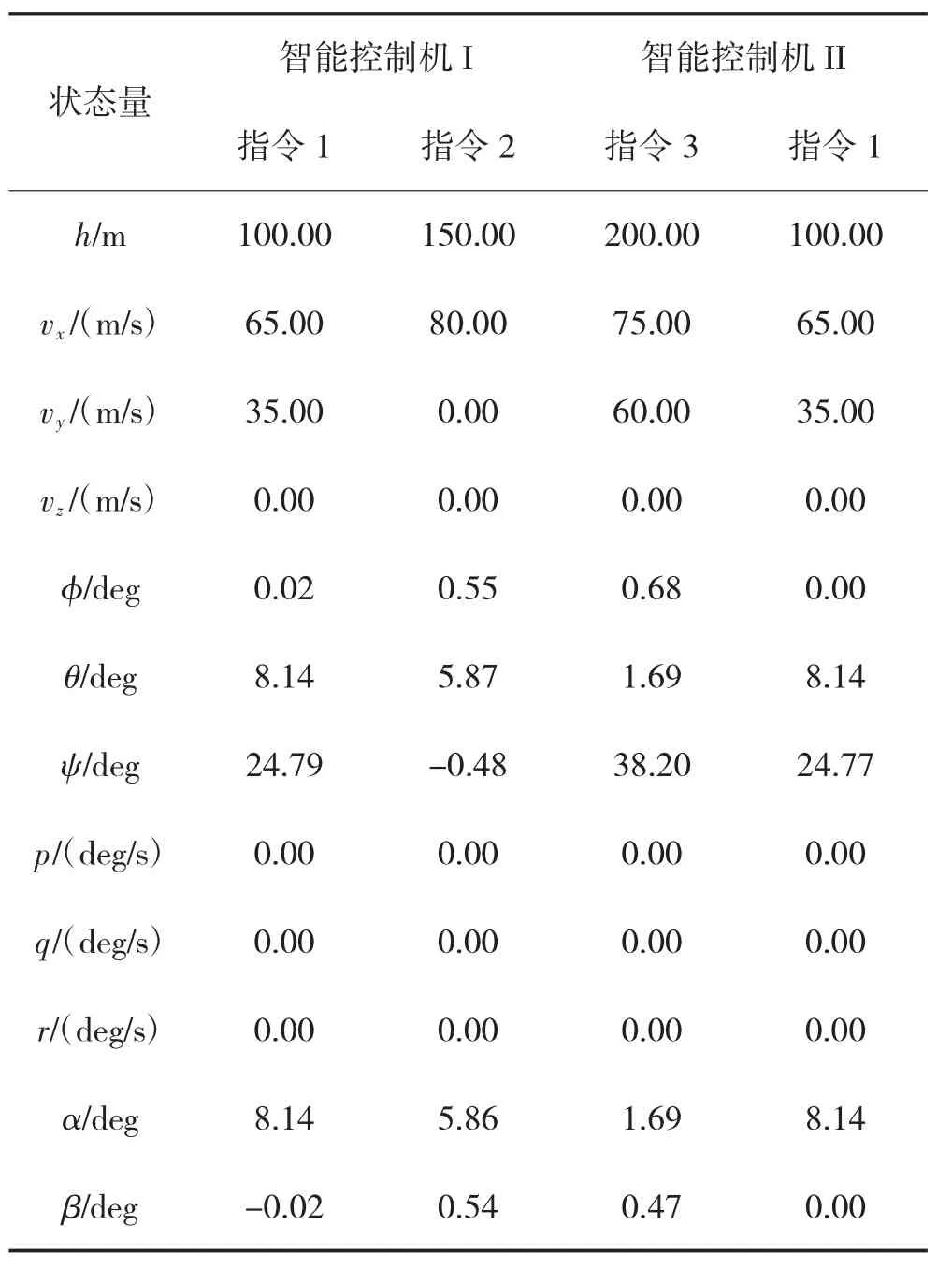
表2 非标称指令下飞行器稳定巡航时的状态结果Table 2 The aircraft stable cruise states under nonstandard commands

5 结论

将神经网络用于控制器设计并不是新颖的做法,但在深度强化学习技术以前研究的神经网络控制器中,神经网络主要用于逼近系统模型,然后结合传统控制器进行控制以改善控制品质,或者针对具有特殊逆结构的系统对象进行控制,这两种方式实质上都是对系统模型的逼近.本文直接基于深度神经网络对控制机进行建模,研究了基于强化学习的固定翼飞行器巡航飞行智能控制机设计问题,通过利用深度神经网络的泛化能力对理想控制器进行逼近,发展了引入偏航角误差作为输入量的智能飞行控制机,有效减小了飞行器飞行中的侧滑,实现了巡航飞行的一体化控制.相较于四旋翼飞行器的飞行控制,固定翼飞行器的控制要复杂很多,需要同时考虑气动力与气动力矩的平衡,尤其全尺寸飞行器的训练周期相对于小型飞行器更是大大增加.本文研究表明在控制机的可拓展性与零侧滑控制目标间存在一定矛盾,此外由于奖励函数中没有考虑对控制量的惩罚,飞行器动态过渡过程的品质还不太良好,未来将进一步深化研究,发展具有良好控制品质与鲁棒性能的智能控制机,探索具有远景应用意义的智能飞行控制机开发流程,促进后续决策级层次任务智能实现的研究.